基于复杂网络理论的黑启动电网划分方法

付诗铭，许傲然，高 阳，刘宝良，袁小华

（沈阳工程学院a.研究生部；b.电力学院；c.科技处，辽宁 沈阳 110136）

当电网在发生大的干扰或故障后而造成大规模停电时，可以通过黑启动方案使系统恢复。电网中有自启动能力模块，能使设备逐渐启动并恢复系统。为了加快恢复过程，可以将网络划分为几个子区域，其中黑启动单元可以恢复相应的负载。当一些子区域以稳定状态运行时，准同步并行设备可以实现两个子区域之间的网格连接。电力系统分区方法有两种主要类型：基于行政区划或管辖范围的固定分区方法，以及基于事故后电源故障信息的动态分区方法。当发生特别严重的停电、地震和台风时，由于通信系统无法获得足够的信息，将导致动态分区方法无效。所以，电网应该密切关注预定的固定分区方案。传统的分区方法是机械分区，不能描述内区的紧密度。

复杂网络理论是在社会、自然和工程系统中研究区域网络，旨在揭示网络功能与结构特征之间的联系。随着小世界网络和无标度网络模型的建立，该理论在许多科学研究领域受到越来越多的关注。大量研究表明，电力系统作为大规模复杂人工网络之一，具有世界网络小、社团结构复杂等特点。社团结构实质是复杂网络中的一种拓扑特性，它自动将网络划分为多个子网。该结构具有典型特征，即社团内部节点之间联系紧密，而社团之间的联系相对稀疏，该特性与网格划分的要求高度相似。这种特性为电力系统划分、研究提供了新的途径，有助于克服传统划分方法的不足。

本文提出了一种基于复杂网络理论的黑启动电网分区算法。该算法将分区过程分为两个阶段：第一阶段应用分裂算法，根据黑启动单元的数量合理确定黑启动阶段的最大分区数；第二阶段使用凝聚算法，根据加权模块组合相邻区域，最终确定最优分区方案。

1 社团结构

社团结构是复杂网络理论中最重要的分支，已被广泛应用于社会关系、互联网和商业行为聚集等领域，它也逐渐被引入到电网的复杂行为研究中。由一些顶点构成特殊集合，在特殊集合中存在集合中的顶点之间的紧密接触以及顶点外部集合之间的相对较小的接触，由此网络可以划分为由一些特殊集合组成的社团结构，如图1所示。

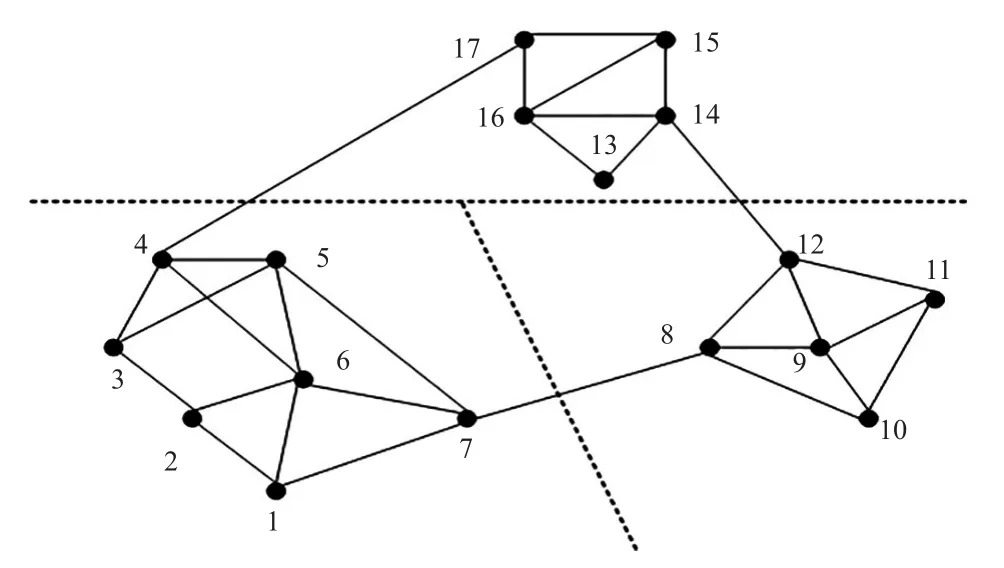
图1 社团结构

目前，最常用的社团结构描述指标是模块度，是由Girvan和Newman提出的，通常称为Q函数。模块度是指用给定社团内边缘的分数减去边缘随机分布的预期分数。对于给定的网络顶点划分为若干个模块的情况，模块度反映了模块内边缘的集中度，而不是与模块无关的所有节点之间链路的随机分布。模块度公式为

式中，节点i和节点j之间的线的权重是Aij；ki=是连接到节点i的所有线的总和权重；m=是所有线的总权重；ci是节点内的社团结构的序列号。如果节点i和节点j在相同的社团结构中，那么果所有节点保持不变并形成随机网络，则是节点i和节点j之间的线路的权重期望。

模块度的范围为0～1，如果社团结构中的总权重不大于随机网络的期望权重，则Q=0。越接近上限Q，社团结构越明显。通常，当Q大于或等于0.32时，表明分区方法是更合适的方法。根据上述描述的模块度的特点，通过比较不同网络的最大模块度来评估其结构可分性。Q的局部峰值通常不大于2，因此很容易根据Q进行分区。总之，根据模块度的峰值，可以选择最佳分区数来确定最佳分区模式。

2 电网分区方法

2.1 线的权重

复杂网络理论使用节点集V、边集S和边权wij来描述复杂网络。复杂电力系统模型通常将发电机和负荷视为节点，将线路视为边缘。双电路或多电路通常合并为一个边缘。传统方法使用线路电抗的倒数作为重量。根据流量分布和网络拓扑结构，定义了线（i，j）的权值为

根据电路方程，可以清楚地描述各厂用电负荷的比例。该方法量化了每条线路在整个电网潮流中的作用。

2.2 重量模块度

线的权重决定节点之间的连接和社团分区过程中连接的强度，它能够更准确地划分网格。根据权重，本文将重量模块度重新定义为式中，αs是社团中总线重量s与网络中总线重量之比；βs是连接到社团s中的节点i的线路的总重量与网络中的总线路权重之间的比率。

2.3 分区方法

基于节点之间连接的相似性或强度，可以使用某种算法将网络划分为多个子组。根据分区过程是将网络中添加边缘还是从网络中去除边缘，分为分裂算法和凝聚算法。仅使用分裂算法或凝聚算法是不够的，本文使用了两种算法。这两种算法都有一定的优点和缺点，因此，本文使用了两种不同阶段的算法的结合。在黑启动初始阶段，使用分裂算法建立初始区域，然后使用聚合算法将竞争区域合并。对于两种算法的结合，计算出初始区域的权重模块度，记为Q0。

此外，该算法合并任意两个连续区域p和q作为区域(p,q)，计算区域(p,q)的模块程度为Qtemp(p,q)。如果区域m和n合并为区域(m,n)，且区域(m,n)具有最大模块度max(Qtemp)，则该算法合并区域(m ,n )，并定义 Qr=max(Qtemp)，其中，r是迭代次数。如果g次迭代后的模块度Qg等于迭代过程中的最大模块度，则其对应最优分区方案。电网分区方法的具体过程如下：

1）初始化参数，迭代次数r=0，初始分区号N=ng，其中ng是黑启动单元的数量；

2）计算初始分区Q0的模块度；

3）构 造 边 权 重 矩 阵 Wnl×nl，nl是 阶 数 ，wij=

4）计算任意两个区域p、q的模块度为Qtemp；

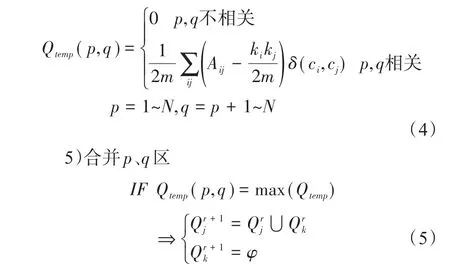
7）返回步骤4）直到初始分区号N=1；

8）确定最佳分区方案。如果是Qt=r=m0～anx-1(Qr)，则分区方案是最终结果。

2.4 分区结果评估

如果任何节点i和社团s满足 Q(i∈s)＞Q(i∉s)，那么，与社团s内其他节点的连接都比与社团s外其他节点的连接更近，这说明社团s具有强大的分区结构。分区方法应确保所有社团都具有强大的分区结构。本文采用A和B等指标来评估分区方法的结果。A是社团中边缘数量与网络中具有相同节点的边缘总数之比，它反映了社区内部的连接紧密度。B是社团与社团之间边缘数量与网络边缘总数之比，它反映了社团之间的连接紧密度。如果A值较大且B值较小，则分区方法更有效。

3 研究案例

本文采用IEEE 39-bus测试系统来验证分区方法的有效性，测试系统的参数可参考文献。纸张和传统阻抗之间的介质用于描述线的权重，相应的分区结果如图2和图3所示。

图2 阻抗重量的分区结果

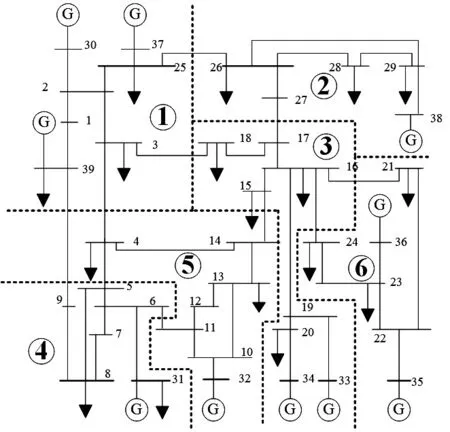
图3 中间权重的分区结果

表1 两种方法的比较

表1用A、B和Q评估了两种分区方法并对结果进行了比较。在使用相同的网格情况下，这两种方法将测试网络划分为6个区域。图2和图3显示了两个权重算法有一些相似之处，这表明两个模型可以反映电网的局部特征并呈现局部社团结构。根据上述的分区结果评估，可以得出图3中的6个部分都是紧密的社团结构，图2中的2和6是弱社团结构，这表明方法1具有较差的划分效果，利用中间权重可以更有效地测量节点之间的连接强度。

表1中的数据显示方法2具有比方法1更大的A和Q，节点在社团内更紧密地连接。方法2的B越小，表明社团之间的联系越多，社团之间的流量耦合关系就越弱。

4 结论

本文运用复杂网络理论，对电网进行黑启动分区。该分区方法使用了两种不同阶段的分裂算法和凝聚算法的结合。采用IEEE 39总线对系统进行测试和仿真，验证了该方法的可行性。通过图表对比了两种分区方法的内部社团结构的紧密度。