基于遗传算法优化小波神经网络的短期光伏功率预测研究

张德天，高 阳，宋 阳

（沈阳工程学院 a.研究生部；b.科技处，辽宁 沈阳 110136）

由于光伏电站的输出功率受气象条件影响较大，导致其出力不稳定，所以在大规模光伏厂站接入电网时，会给电网的平稳运行带来严重挑战，甚至会造成国民经济的损失。对光伏电站输出功率的准确预测，不仅有利于电力系统调度部门对保证电网平稳运行进行的合理安排，也有利于光伏电站的自身收益［1-3］。基于此，光伏功率的准确预测已经成为电网、光伏厂站、第三方服务企业共同面对的一项重要课题。

光伏发电功率预测是通过采用天气预报数值的或者利用数学统计的方法来预测未来某段时间内的光伏发电系统的输出功率［4］。从预测原理角度出发，光伏发电功率预测大致可以分为物理方法、统计方法和学习方法；从预测时间角度出发，光伏发电功率预测可分为超短期功率预测、短期功率预测和中长期功率预测［5］；从预测方式角度出发，光伏发电功率预测可分为间接预测和直接预测［6］。虽然我国光伏产业较国外起步晚，但是经过我国学者以及光伏人长期的探索研究，到目前为止我国在光伏预测方面的研究已经取得了实质性的进展［7］。文献［8］提出了一种经遗传算法优化的模糊径向基神经网络的光伏功率预测模型，该模型对光伏电站并网功率进行有效调节，从而达到平滑光伏功率波动的目的，但是在一定程度上的泛化能力不高，主要原因是在一些特定的区域其天气数据具有独特性，并不一定满足数据平滑的特点。文献［9］通过引入附加动量和变学习率算法对Elman神经网络进行优化，使得模型具有更高的训练性能，但是不足之处在于对训练数据的预处理做的不够。文献［1］提出了一种智能水滴算法优化的Elman神经网络模型，该模型在做数据分类时只考虑了按天类型分类，而忽视对季节的影响。文献［10］提出了一种优化的灰色模型与粒子群算法优化的BP神经网络的组合算法，实验结果表明该方法的预测精确度较高。文献［11］提出组合权重相似日选取方法及光伏输出功率预测的模型，该模型通过将主观权重与客观权重有效结合来选出相似度较高的相似日，但是难点在于各基值点的选取以及需要海量的历史数据作为依据。由此可见，光伏功率预测是一个涉及因素多、过程复杂程度高的非线性问题，要想提高预测的精确度，除了要有适合的算法模型，还要有合理的、可靠的数据源［12］。

本文提出了基于遗传算法优化小波神经网络的光伏电站输出功率预测方法。首先，对样本数据进行数据预处理，选出合理的样本数据；其次，通过数据分析得出影响光伏出力的主要因子；最后，利用遗传算法得到适应度更好的权值和阈值，赋值给小波神经网络，从而达到优化的目的。通过对西北一光伏厂站数据仿真分析表明，遗传算法优化小波神经网络的模型具有较高的预测精度。

1 光伏发电出力的主要影响因子

本文以青海海南某一光伏电站为例（N：35.6，E:100.3，海拔3 000 m）。该厂站装机容量为50 MW，样本数据点每隔15 min取1个，研究的时间段为每天6:00～20:00，即一共57个数据点。该电站的数据采用NWP数据、气象数据。数据的预处理主要针对的是原始数据中重复、异常以及限电的数据，主要是对这些数据进行删除、补充、修正。具体流程如图1所示。

由于该厂站位于青海，属于高海拔、干燥地区，气候特点比较独特，故把每年中的3～5月份当作为第一季度，6～8月份当作第二季度，9～11月当作第三季度，12月以及下一年的1、2月份作为第四季度。图2为晴天、多云、雨天3种天气状态下该电站的输出功率，图3表示不同季度下该光伏厂站的平均出力情况。从图2中可以直观地看出，晴天的输出功率最多，多云次之，雨天最少，所以对光伏电站进行输出功率预测时要考虑不同天气状态的影响。从图3中可以看出，第一季度的出力最多，第三季度的出力最低，由此可见该厂站的出力与季节也有关系。

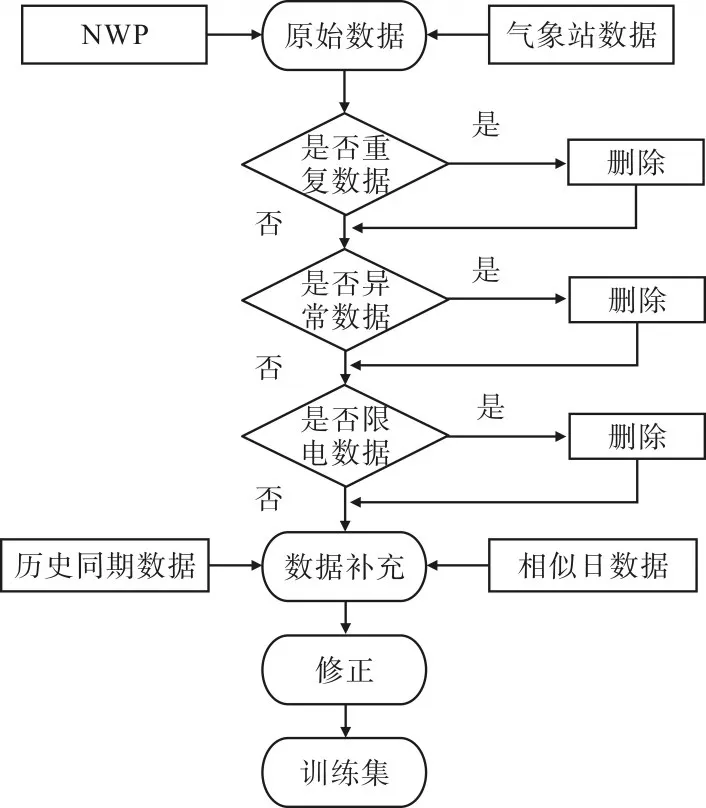
图1 数据预处理流程

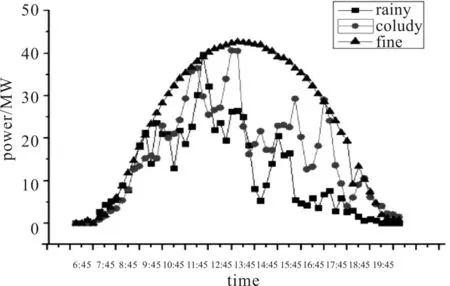
图2 不同天气情况下光伏电站的输出功率曲线

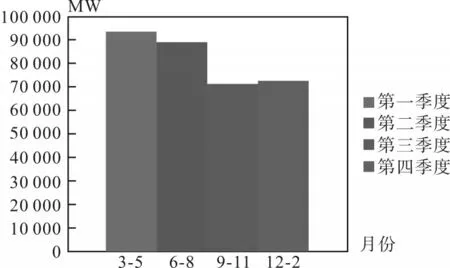
图3 不同季度下光伏电站的输出功率曲线

图4 为不同天气情况下光照强度、温度、湿度与光伏电站出力情况曲线图。从图中可以看出，在晴天的时候温度与光照强度对光伏电站出力作用较大，而湿度较小；在雨天的时候湿度对出力的作用变大，且呈现负相关趋势；在多云天的时候光照强度对厂站出力起主要作用，且湿度的作用大于温度。

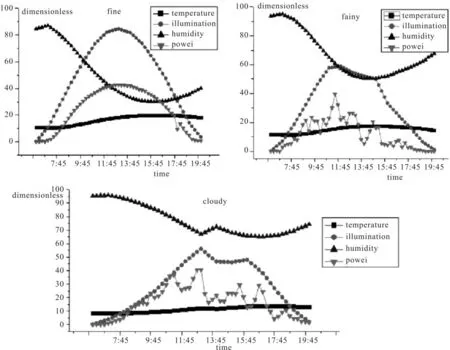
图4 不同天气情况光照强度、温度、湿度与光伏电站出力情况曲线

基于以上分析，影响光伏出力的气象主要为各季节以及各季节中不同天气条件下的光照强度、温度和湿度。

2 小波神经网络

小波神经网络是一种以BP神经网络拓扑结构为基础，小波基函数作为隐含层节点，信号前向传播的同时误差反向传播的神经网络［13］。其拓扑结构如图5所示。

图5 小波神经网络拓扑结构

图5 中，X1，X2，…，Xk是小波神经网络的输入，Y1，Y2，…，Ym是小波神经网络的预测输出，ωij和ωjk分别为小波神经网络的输入、输出权值。当信号输入为xi（i=1,2,…,k）时，隐含层的输出为

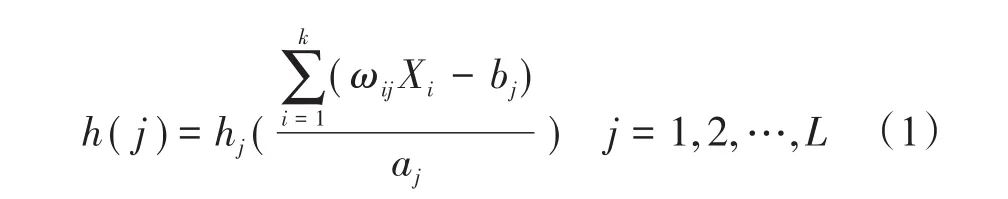
式中，h(j)为隐函数第j个节点输出值；ωij是输入层到隐含层的权值；bj是小波基函数的平移因子；aj是小波基函数的伸缩因子；hj是小波基函数。

此外，小波神经网络的输出层计算公式为

式中，ωij为连接隐含层和输出层之间的权值；h(i)为第i个隐含层节点的输出；L为隐含层的节点数；m为输出层的节点数。

小波神经网络的优点是结合了小波分析和神经网络的特点，有较好的自主分辨性和容错能力，但是在处理维数较高、数值较大的数据时，会使得网络的收敛速度大大降低，此外还会导致网络参数初始化不合适而造成函数不收敛。故需要对其进行优化。

3 遗传算法优化小波神经网络

3.1 遗传算法原理

遗传算法（Genetic Algorithms）是上世纪60年代由美国提出的一种并行随机搜索最优化方法。该方法按照生物进化论的观点，使得适应度好的个体被保留，适应度差的个体被淘汰，这样新的群体既继承了上一代的信息，又优于上一代，反复循环，直至满足条件为止［14］。其基本操作分为选择操作、交叉操作和变异操作［15］。

3.1.1 适应度函数

适应度函数是把预测输出和实际输出之间的误差绝对值和E作为适应度值F，计算公式为

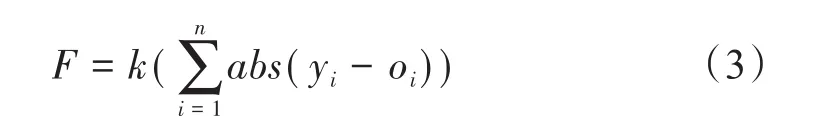
式中，n为网络输出接点数；yi为小波神经网络第i个节点的实际输出；oi为第i个节点的预测输出；k为系数。

3.1.2 遗传算法的选择操作

选择操作是指从原始群体中以一定概率选择个体到新的群体中，个体被选中的概率跟适应度有关，适应度越好，被选中的概率就越大。具体采用轮盘赌法。每个个体i的选择概率pi为

其中，N为种群个体数；Fi为个体i的适应度，且在光伏功率预测中要求适应度越小越好，故新的适应度变为

3.1.3 遗传算法的交叉操作

交叉操作是指从个体中选择两个个体，通过两个个体的染色体交换组合，产生新的优秀个体。具体操作为采用实数交叉法。公式（7）表示第k个染色体ak和第l个染色体al在j处交叉的具体操作方法。

式中，b是［0，1］的随机数。

3.1.4 遗传算法的变异操作

变异操作是指在某一个体中选择染色体中的一点进行变异，产生更加优秀的个体。公式（8）表示对第i个个体中的第j个基因进行变异。

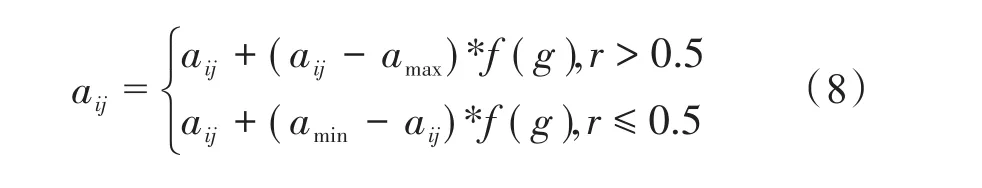
式中，amax为基因aij的上界；amin为基因aij的下界；f(g)=r2(1-g Gmax)2；r2为当前迭代的次数；Gmax为最大进化的次数；r为［0,1］的随机数。

3.2 算法流程及步骤

遗传算法（GA）优化小波神经网络分为初始小波神经网络的确定、遗传算法优化和优化后的小波神经网络预测3部分［16］。首先是遗传算法的编码，主要是依据数据预处理后的原始数据以及初始小波神经网络的权值和阈值；其次是进行种群的初始化并且以小波神经网络的初始误差作为适应度，经过选择、交叉和变异操作找到最优适应度值；然后经过解码把得到的最优适应度赋值给小波神经网络，从而继续对样本进行训练；最后输出预测结果。

基于以上分析，可以得出基于遗传算法优化的神经网络算法流程，如图6所示。

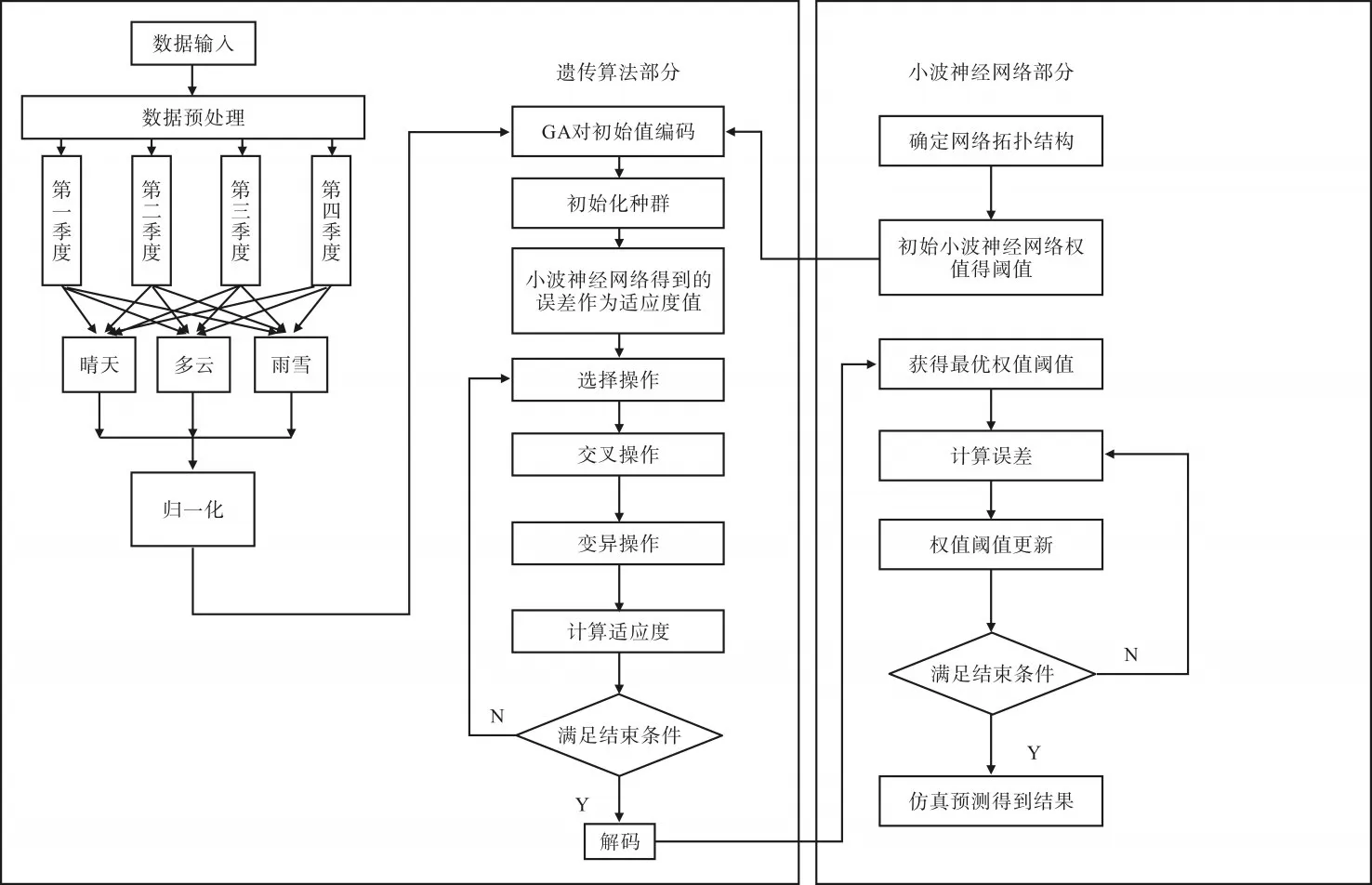
图6 遗传算法（GA）优化的小波神经网络流程

其主要步骤如下：

1）输入数据预处理后的原始数据，并且按照不同的季节以及天气状况进行分类。

2）利用公式（9）对输入的各类型数据进行归一化处理。

3）将初始的小波神经网络的权值、阈值和归一化的数据结合考虑，进行遗传算法的实数编码。

4）对经GA编码后的个体进行随机种群初始化。

5）对经初始化后的种群进行选择、交叉、变异操作，根据式（3）和式（6）把预测功率与实际功率差绝对值求和的最小值选出，从中找出最优个体。

6）对步骤5）中选出的最优个体适应度进行解码，并且把由此得到的最优权值和阈值赋值给原始的小波神经网络进行模型训练。

7）利用西北新细则中的短期功率考核指标设置约束条件，进行训练，若满足设置的误差需求则输出；若不满足，则返回步骤6）继续训练。

3.3 输入因子以及模型参数设置

本模型是对各季节下按不同天气类型进行分类的，把预测日的前一日6:00～20:00中每隔15 min的气象数据作为输入样本，选取经数据预处理后的温度、湿度、光照强度及历史的光伏功率作为模型的4个输入量，把被预测日功率作为输出量。所以，本模型为4输入1输出的模型，设置种群的初始值为30，进化次数为50，交叉概率为0.4，变异概率为0.2。

4 预测实例以及结果仿真

4.1 仿真预测

以青海海南某一光伏厂站6～8月份的数据为实验样本，分别做晴天、多云、雨天3种天气情况下的实际输出功率3种模型预测曲线，如图7所示，其中取30天晴天数据，20天多云数据以及15天雨天数据进行建模分析。把这3类天气情况下的最后一天数据作为测试数据，剩余天数作为训练数据，利用Matlab进行仿真处理。

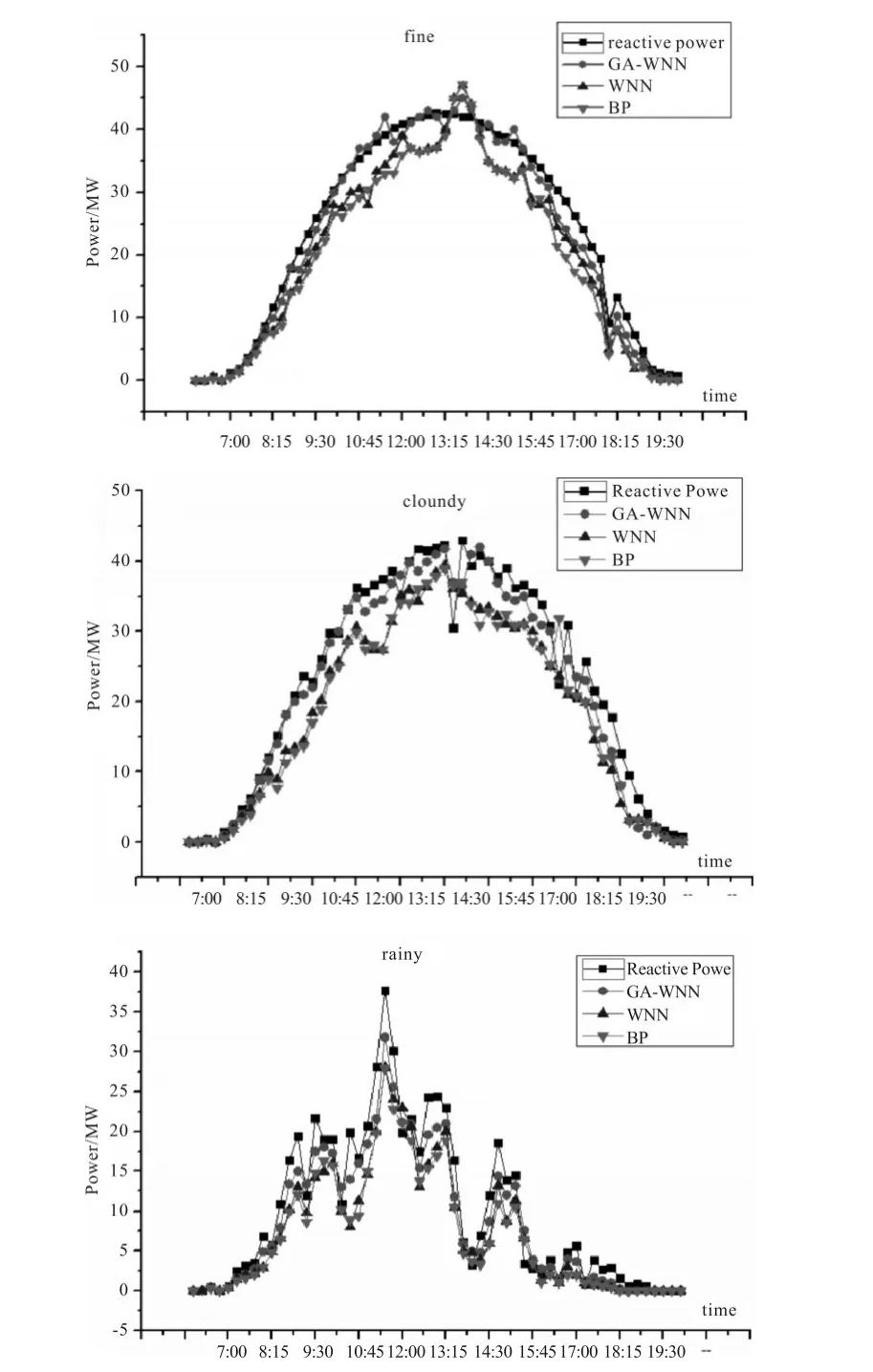
图7 3种天气情况下3种模型的预测曲线

4.2 预测结果分析

为了验证遗传算法（GA）优化的小波神经网络模型的预测性能，根据西北地区新细则要求，对短期预测日均方根误差不予考核，月平均绝对误差不予考核，改为对预测单点的偏差考核，而且单点偏差不超过20%［17-18］。从对应3种类型天气下的模型的短期单点偏差、适应度曲线进行分析。由于篇幅有限，只对晴天时候小神经网络（WNN）和遗传算法优化的小波神经网络（GA-WNN）的适应度曲线进行分析。

1）晴天情况下适应度曲线分析

图8、图9分别为在晴天情况下遗传算法优化的小波神经网络（GA-WNN）和小波神经网络（WNN）的适应度曲线图。

图8 GA-WNN适应度曲线

图9 WNN适应度曲线

通过图8、图9对比可以发现，在进化50次的相同条件下，GA-WNN最佳适应度和平均适应度都好于单纯WNN的适应度，根据式（3）以及式（6）可知，经GA修正的WNN短算法模型实际期望出力与预测出力更为接近，从而使得预测更加精准。

2）短期光伏预测单点偏差百分比

由于西北短期考核细则主要考核每天8:00～18:00单点偏差不超过20%，所以单点误差百分比考察公式为

3种模型下，对应不同天气情况的单点偏差百分比如表1所示。

表1 不同模型不同天气单点偏差考核表

通过对表1分析可知，3种模型在晴天情况下都能满足预测要求，但是GA-WNN的预测精度要明显好于WNN与BP的预测精度，其多数点的误差都集中于0%～9%的范围内，模型稳定性较好。在多云与雨天的时候，只有GA-WNN能满足考核要求，但是也可以发现，多数点的误差都集中在10%～20%，甚至偏向20%。

5 结论

本文提出一种基于遗传算法（GA）优化小波神经网络（WNN）的光伏电站输出功率的短期预测模型，使用遗传算法（GA）得到的最优权值和阈值对小波神经网络进行赋值，再结合西北地区气候环境的特殊性，考虑了不同季节、不同天气条件下多种因素影响光伏厂站的输出功率，进而把预测模型分为不同季节、不同天气下的3个子模型。预测结果表明，与BP神经网络、WNN相比，GA-WNN具有更高的预测精度，日短期功率曲线更符合实际值，且能满足西北地区新细则对短期光伏功率的考核要求。但是，在多云和阴雨天气条件下，该模型的预测误差明显要低于晴天的时候，造成这种现象的原因主要是训练样本数量不是足够多，西北环境的复杂多变，以及模型仍有要完善优化的空间，因此如何克服这种情况下的预测难度是下一步研究的重点。