Jatigede大坝施工期心墙孔隙水压数值模拟研究

翟 旻， 王 鹏

(四川省水利水电勘测设计研究院，四川 成都 610065)

0 引 言

心墙堆石坝是由相对不透水或弱透水的土质心墙和抗剪强度较高的堆石体坝壳组成的。堆石坝心墙在施工碾压时饱和度达到80%以上时，心墙中的孔隙水压消散很慢，施工中会产生的高孔隙水压将降低心墙的有效应力，从而影响坝体的稳定和强度[1-3]。本文以监测资料为基础，通过建立三维固结数值模型分析施工期砾石土心墙的应力应变及孔隙水压消散情况，并与实测资料进行对比分析，以期更深入理解砾石土心墙的应力应变和孔隙水压特征及形成机制。

1 工程概况与监测设计

1.1 工程概况

Jatigede水库工程位于印尼西爪哇省INDRAMAYU县境内，挡水大坝为粘土心墙堆石坝。大坝坝体断面分为6个区，最大坝高110 m，坝顶高程265 m。

1.2 坝料情况

大坝心墙料属高液限粉土，红土化、具团粒结构，压实干密度底，压缩试验显示高应力下会发生大变形，坝体其它分区由安山岩加工而成，石料饱和抗压强度64.79 MPa～ 104.19 MPa，均大于60 MPa，为坚硬岩石。

由于本工程地处热带地区，雨季不宜施工，旱季心墙粘土含水率也较高，因此，本工程心墙基本是在最优含水率的湿侧进行填筑，施工期心墙饱和度高于90%。由非饱和度土力学可知，当土体中的含水率很高时，土体中的气相很小且被液相所包围，构成准二相体系。因此，在本论文中将心墙近似地视为处于饱和状态。

1.3 监测设计

为监测坝体内应力应变，及孔隙水压情况，本工程在最大坝高断面桩号1+100剖面处设置的监测设备包括：垂直测斜管、界面应力计、总应力计、土压力计组和渗压计。桩号1+100剖面的监测布置图如图1所示。

2 施工期心墙应力应变及孔隙水压数值模拟

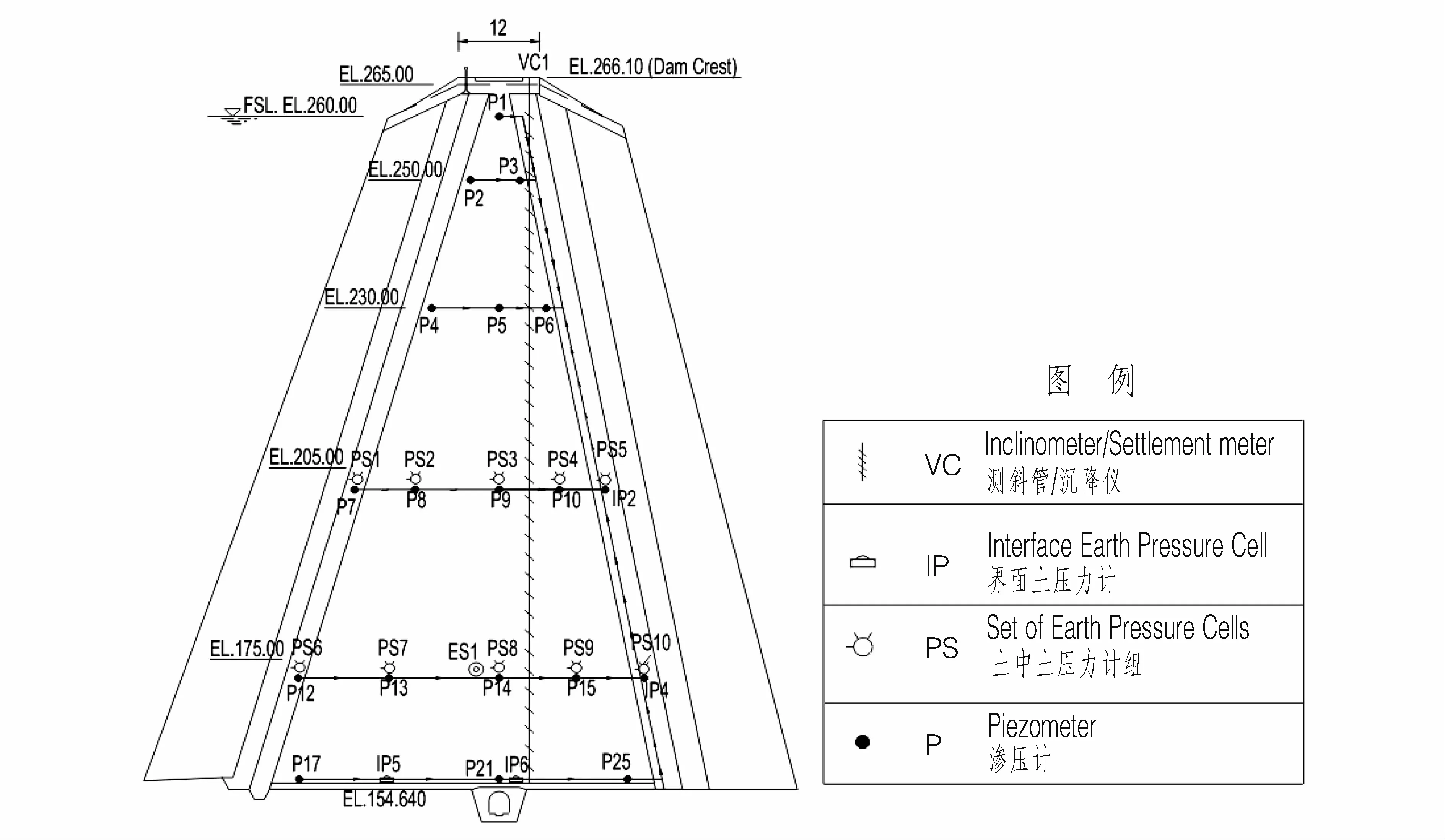
图1 桩号1+100处监测剖面图

2.1 计算原理

根据土的变形原理，土的初始变形和固结效应可以采用Biot固结理论[4]进行描述，该理论通过建立土体的弹性平衡方程式，同时根据土体排除的水量等于土体骨架体积改变的关系，建立了连续方程，两者联立可以同时求解出土体中的应力、应变和孔隙水压，Biot固结理论的基本方程如下。

平衡方程：

(1)

连续方程：

(2)

上式中：u、v和w为土体三个方向的位移，σ为孔隙水压，k为渗透系数，ε为土体的体积应变，G为剪切模量，υ为泊松比，α为与土体弹性参数相关的常数。

但Biot理论假定土体骨架是线弹性的，不能准确地描述堆石坝中土体的非线性应力应变特性。根据国内工程经验，本文采用Duncan-Chang模型[4]确定Biot基础方程中的变形模量参数，再用有限元的基本理论求解Biot方程。

2.2 模型与参数

在坝体应力应变参数的选择上，需要考虑工程规模、施工工期及环境气候等因素。本工程位于热带地区，雨季降雨频繁，不能进行心墙填筑，即使是旱季空气湿度也较大，土质心墙不易翻晒，填筑时含水率基本都高于最优含水率。另外，本工程坝体施工工期长达2年4个月，施工过程中，坝体内应力调整明显，心墙存在相当程度的排水固结。参照相关文献[5]，本工程采用固结不排水剪模型参数进行数值模拟，坝体各个分区的模型参数如下表1所示。

根据工程的实际施工进度，坝体填筑过程如下图2所示。坝体高度110 m，计算模型中划分为14层，每层平均厚度7.86 m，以模拟坝体的分层填筑。由于坝体除心墙以外，渗透系数均大于10-4cm/s，孔隙水压消散很快，因此，在计算模型中设置为非固结单元，而心墙土体为固结单元。

表1 坝体各分区E-B模型应力应变参数表

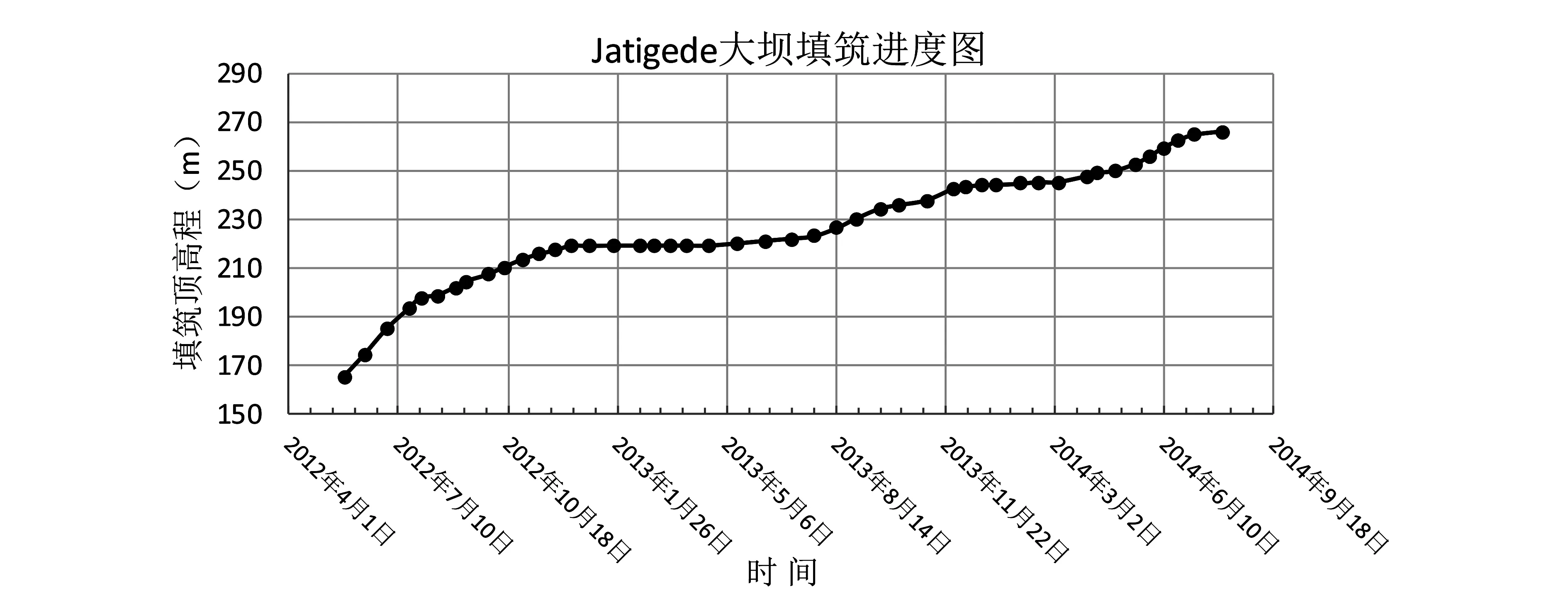
图2 最大断面处坝体填筑过程图

图3 竣工期(2014年9月)最大断面坝体第一主应力图

图4 蓄水前(2015年9月)最大断面坝体第一主应力图

2.3 计算结果

(1)坝体应力

竣工期和蓄水前坝体内部大主应力最大值均出现在坝体底部心墙两侧的反滤过渡区，分别为2.69 MPa和2.86 MPa，相同高程的心墙内部第一主应力(总应力)却只有1.34 MPa和1.26 MPa，反滤过渡层存在应力集中，应力等值线在反滤过渡层与心墙之间呈驼峰状分布，出现明显的应力拱效应。

对比竣工期和蓄水前心墙底部和相同高程处心墙两侧反滤料区中的变形和第一主应力可以看出，从竣工期(2014年9月)到蓄水前(2015年9月)，坝体心墙固结沉降，心墙有向下变形的趋势，而反滤过渡料由于变形模量高于心墙料，在其与心墙接触的上下游表面产生剪应力，“钳制”了心墙的向下变形。从而出现从竣工期到蓄水前心墙的总应力降低的情况，这说明心墙固结过程中消散的孔隙水压没有完全转换为心墙本身的有效应力，有部分应力通过“拱效应”产生的剪应力传递给到了坝壳料区。

(2)心墙孔隙水压

竣工期心墙内的孔隙水压呈“中间高两侧低，底部高顶部低”分布，孔隙水压与心墙内部至两侧反滤过渡料渗透路径的长度成反比，符合土体固结理论。心墙内最大孔隙水压点位于坝高1/5之一坝体高度中部，最高压力点没有位于坝体底部的原因是计算模型中岩石地基渗透性大于10-5cm/s，可消散部分孔隙水压。从图5中可见，竣工期心墙内计算最高孔隙水压水头为75 m，坝体填筑到顶后的一年内，心墙固结沉降，最高孔隙水消散为38.5 m。

图5 竣工期(左)和蓄水前(右)心墙内孔隙水压分布图

3 心墙应力及孔隙水压对比分析

本文根据工程特点选择心墙底部坝轴线与建基面交点处作为代表，分析施工开始至蓄水前大坝的应力应变及空隙水压力随施工进度的变化情况。该处埋设有土压力计IP6，可反应心墙底部随填筑高度变化的心墙基底总土压力。在IP6处还埋设有P21渗压计，用于反应该处孔隙水压的变化情况。IP6所测得总土压力减去P21监测的渗压即为心墙底部Z向土压力的有效应力，由于该处荷载基本对称，该值也近似与第一主应力相同。IP6和P21实际观测值与计算值对比情况如图6及图7所示。

由图6可见，心墙底部总应力监测值和计算值历时曲线反应出相同的规律。从2012年5月至2012年11月大坝填筑的第一旱季期间坝体上升速度较快，当大坝顶高程上升至213 m时，心墙底部竖向总应力随大坝增高逐渐增大至1.1 MPa；2012年11月至雨季末的2013年7月(该年度雨季较长)大坝填筑上身速度慢，心墙底部总应力呈下降趋势，原因在于大坝上部加载速度慢，而心墙中的孔隙水压则在不断消散，部分心墙的自重应力通过反滤过渡料与心墙之间的剪应力传递转移到坝壳。从2013年8月开始大坝恢复填筑至2013年11月大坝填筑至242 m，心墙底部总应力缓慢上升至1.3 MPa；第二个雨季后，大坝填筑到顶高程266 m，由于本阶段大坝填筑速度慢且坝体顶部体积小，加载相对较小，心墙底部的总应力增加幅度较小，心墙底部竖向总应力在坝体填筑到顶时达到最大值1.4 MPa，随后在大坝蓄水之前大坝心墙一直处于固结排水阶段，由于心墙与坝壳料之间的“拱效应”，在这个阶段心墙底部总应力呈下降趋势，但由于心墙渗透系数很小，孔隙水压消散很慢。

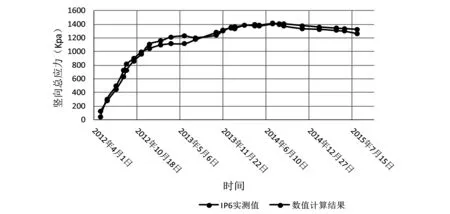
图6 心墙底部竖向总应力监测值与数值计算对比图

图7 心墙底部孔隙压力监测值与数值计算对比图

从图7可见，相较于心墙底部总应力实测值与计算值的吻合情况，心墙底部的孔隙水压计算值历时曲线与实测值相差较大，主要不同体现在孔隙压力计算值随坝体增高增大得更快，在第一个旱季连续施工末期，孔隙水压计算值接近0.8 MPa，而实测值则为0.6 MPa，而2014年5月坝体填筑到顶至大坝蓄水前，孔隙水压计算值较实测值消散速度更快，至2015年8月蓄水前，心墙底部孔隙压力实测值维持在0.6 MPa，而孔隙压力计算值则消散为0.4 MPa。但总体上来看，心墙底部孔隙压力计算历时曲线所反映的孔隙压力形成和消散规律与实测曲线相同。施工前期河谷宽度小，坝体填筑上升速度快，心墙底部孔隙水压来不及消散，孔隙压力增加快并达到一个峰值，第一个雨季大坝上升速度慢，孔隙水压不但不上升反而缓慢消散，再进入第二个旱季大坝继续填筑，孔隙水压相应增大至大坝填筑到顶时达到最大值。最后从填筑完成期到蓄水前，心墙停止加载，处于固结排水状态，心墙底部孔隙水压逐渐消散。

图8 心墙底部有效应力监测值与数值计算对比图

图8显示了心墙底部竖向有效应力计算值与实测值的对比情况。从图中可见，在第一个旱季坝体填筑速度较快的阶段，数值计算所得孔隙压力偏高，造成心墙底部有效应力较实测值低。但到坝体填筑到顶时，计算值与实测值逐渐相近，而坝体填筑到顶之后到水库蓄水前，数值计算孔隙水压消散得比实测值快，因而有效应力也相应地增长得更快。到蓄水前，心墙底部的竖向有效应力实测值为0.6 MPa，而计算值则为0.9 MPa。

4 结 论

(1)心墙与坝壳料之间的模量差产生的“拱效应”将显著降低心墙内的竖向应力。从本工程来看，心墙底部的总应力实测值约1.3 MPa，远小于110 m高土体的静土压力。

(2)施工期心墙内将残生高孔隙压力(最大0.82 MPa)，导致心墙内的有效应力很低，心墙的抗剪能力很差。因此，设计中应重视坝体施工期的坝体的临时稳定，根据大坝填筑加载速度和心墙内孔隙水压生产和消散情况，选择代表性施工剖面验算大坝在施工期的稳定性。

(3)基于duncan-chang本构模型的Biot固结方程可以通过有限单元法进行求解，从而获得堆石坝施工全过程心墙应力应变和孔隙压力的演变情况。从本文的计算看，数值计算可以较准确地模拟坝体变形，并反映心墙内应力和孔隙水压变化规律，但心墙孔隙水压的计算值存在较大偏差，原因可能是所采用的是饱和土的Biot固结方程，土石坝心墙在填筑过程中含水率虽然接近饱和，但心墙土体仍是三相状态，土体颗粒间包含有气体，饱和土的Biot固结理论不能准确反映土体颗粒间存在二相流时的孔隙水压演变情况。非饱和土的固结理论及求解方法还值得进一步研究。