巧用前测 促进学生思维发展
2019-11-06左小平
左小平
(南京市五老村小学,江苏南京 210000)
笔者近年来一直利用前测找准学生的认知起点,但如果前测作用仅限于此,似乎不能“物尽其用”。数学是思维的科学,按照本杰明·布鲁姆“教育目标分类学”,数学思维可以分为记忆、理解、运用、分析、评价和创造,其中记忆、理解和运用属于低阶思维,分析、评价和创造属于高阶思维。那么前测不同,学生的思维呈现的方式不一样,水平也不一样。
一、通过找准学生认知的起点激活思维发展的需求
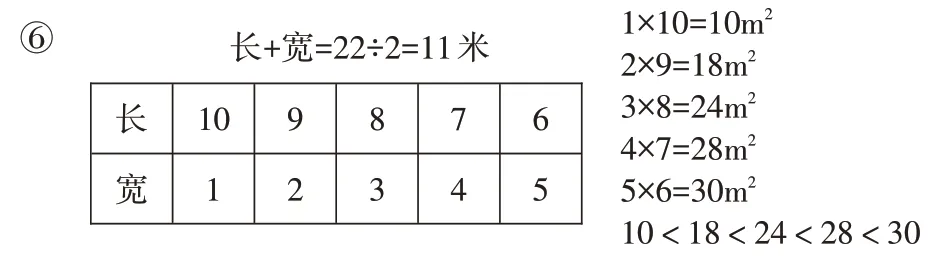
以五年级上册《解决问题策略——列举》为例。前测题目:王叔叔用22根1米长的木条围成一个长方形花圃,怎样围面积最大?
师:仔细观察,想一想根据解题方法不同可以把下面这些作品分成几类?
①22÷4=5.5(米)5.5×5.5=30.25(平方米)
②22
21 1 21×1=21(平方米)
20 2 20×2=40(平方米)
19 3 19×3=57(平方米)
……
12 10 12×10=120(平方米)√
③22×1=22(米)22÷2=11(米)
第一种:宽1m,长10m,10×1=10(m2)第二种:宽2m,长9m,9×2=18(m2)
第三种:宽3m,长8m,8×3=24(m2)第四种:宽4m,长7m,7×4=28(m2)
第五种:宽5m,长6m,6×5=30(m2) 30>28>24>18>10


1×10=10(m2),2×9=18(m2),3×8=24(m2),4×7=28(m2),5×6=30(m2)(面积最大)

生:按解题方法的不同可以分成列式计算、画图和列表。
师:根据大家的分类,选择列式计算的,我们先来看看1号代表作品,仔细看看,你们能猜到他是怎么想的吗?
22÷4=5.5(米)
师:请介绍一下,你当时怎样思考的?
生:22根1米长的小棒,周长就是22米,围成正方形面积最大,所以22÷4=5.5(米)
生:不对,小棒不能折断,不可能5.5 米,而且也不是长方形。
师:你是从题目中哪个关键词看出,长和宽需要取整米数?
生:围成。
师:通过他们刚才的对话,在我们下笔之前你有什么想提醒大家注意的地方?
生:审题要仔细。
师:学习就是这样,这两位同学提供了一个非常有价值的数学问题,并且通过大家自己的交流,他们也弄懂了,这就是学习的过程。
师:④号和⑤号有什么相同和不同之处,你更欣赏哪一幅?
生:相同的地方是都是画图,都是把每一个列举出来。不同的地方,一个列全了,一个没列全。
师:你怎么知道他有没有列全的呢?
生:对比两个作品就知道了。
师:通过对比这两幅图,你有什么提醒大家注意的地方?
生:画图要画全。
师:通过刚才同学的介绍,如果再给你一次机会,你会怎样补充你的图?
师:还有同学列表解决,⑥号和⑦号你更喜欢哪一幅?仔细对比,你有什么想说的?
王叔叔用22根1米长的木条围成一个长方形花圃,怎样围面积最大?
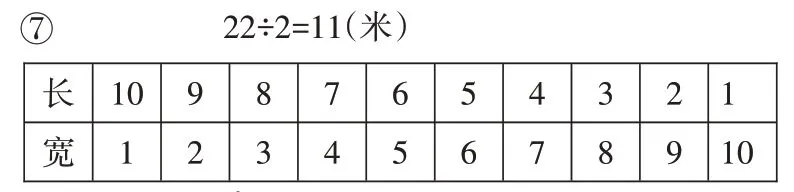
生:第二幅有重复的。
师:你们其他人能看懂吗?能为我们介绍一下吗?
师:你们都比较喜欢第一幅,对于第一幅图,你们有没有什么建议?
生1:他既列表又列了算式可以把面积算出来,在表格下面再画一栏就可以了,这样比较简单。
生2:他的表格中缺少了“单位”。
师:那这样吧,既然你们提出了建议,把你心目中完美的表列出来可以吗?
……

本次前测,在学生多元表征自己的研究结果中,呈现的方式有列式、列表、画图。从中我们不但能够看清学生的思维方式,也能够看出学生思考过程中产生的疑惑和问题,更能看出不同的学生思维过程有相同的地方,也有不同的地方,但学生本人或许没有意识到自己的思维过程是否完整。这就需要在课堂中将不同的思维方式呈现出来,让所有的学生进行探讨与交流,从而激发学生的深度思考,推动学生的思维发展,实现知识的自主建构。
基于这样的想法,本节课教学路径设计为:1.去伪存真,初步分类。层层递进,展开教学,先把有代表性作品一一呈现,让学生从解决问题的方法的角度进行分类,看看能分成几类,让学生初步体会解决问题方法的多样性。2.列式对比,理清题意。课堂教学中将列式解决的三种代表作品置于一屏,通过学生之间的“辩论”,进一步明确题意,为后续的画图、列表等方法的教学铺好道路。3.画图对比,感受“有序”(一幅完整的图和一幅有遗漏的图)。通过学生的对每幅图的解读,老师追问“是否每一种情况都符合要求”这一问题,让学生回到题目中验证,在两幅图的对比中,学生会初次感受到“有序”的优势。4.列表对比,触摸“有序”(一幅完整的表和一幅有重复的表)。5.沟通对比,自主建模。将优化出来的列式列举、画图列举、列表列举进行沟通对比,让学生自主建模,体会不同方法之间的相同之处,进而理解什么是一一列举,以及如何做到一一列举。
二、通过拓宽学生认知的视角搭建思维发展的平台
以六年级上册《稍复杂的分数应用题》一课前测为例。前测题目:岭南小学六年级45个同学参加学校运动会,其中男运动员占女运动员有多少人?
师:昨天,我们花了几分钟解决了一道分数乘法的实际问题,不同的人往往有不同的想法,老师选取了几个比较有代表性的做法,这节课我们就一起来学习一下。

师:仔细观察上面同学的作品,先想一想,他们是用了哪些方法来分析题意的?
生:画线段图,写数量关系。
师:同样是画线段图来分析,这几幅图你更喜欢哪一幅?
生1:我喜欢第二幅,第二幅更清楚,更便于比较。
生2:第二幅不对,看不出谁是单位“1”,这里是把六年级45 个同学看作单位“1”,从第一幅图中能看出男运动员和女运动员所占的份数。
师:听了他的介绍,在画图分析数量关系时,你有什么要提醒大家注意的地方?
生:要看清楚谁是单位“1”,理解部分和整体之间的关系再画图。
师:现在给你一分钟,修改下你自己的图。后面两幅用数量关系表示,能看懂吗?
生:这两种意思其实差不多。
师:画线段图分析和列数量关系分析,各有什么优点,两种方式有没有相同的地方?
生1:列数量关系比较简单,题目怎么说我们就怎么列;画图必须先要理解题意才能正确画出图。
生2:其实画线段图和列数量关系一样,在图中也能看出数量之间的关系。
师:从不同的解题法来分,你可以大致分成几类?
生:可以分成这样几种方法,用分数、份数、比、解方程几种方法解决。
师:那下面,我们就先来学习下不同的方法。
……

从前测中,可以看出学生有能力基于情境提出问题,并能够摒弃原型中非数学属性的相关信息,也能够挖掘情境中的数量关系,用自己的方式表达对题意的理解。能看到学生在分析题意时,呈现出来的可视化思维方式是不同的,有画线段图也有列数量关系,不同学生即使都是画图,也有很大的区别。
教学中,可以通过这样的做法,为学生搭建思维发展的平台。首先,呈现不同学生的做法,对不同的作品有初步的了解,拓宽学生认知的视角。其次,通过这样的问题“同样是画线段图来分析,这几幅图你更喜欢哪一幅?”引起学生的思考,让学生在同伴的解读中明确如何“画好”图,明确后再进行修改,帮助学生逐步提升思维。再次,通过追问“画线段图分析和列数量关系分析,各有什么优点,两种方式有没有相同的地方?”这样的问题以及在线段图与数量关系的对比中,体现学生群体从“数”到“形”,再从“形”到“数形结合”,实现思维上的递进。最后,将学生多种解题方法置于一屏(有利用分数解决、利用份数解决、利用比解决、利用方程解决等多种方法),课堂中不仅关心学生是否会解决问题,更应为学生搭建思维发展的平台,让学生充分表达自己的想法,在学生原有的思维基础之上,深化学生的思维。
三、通过尊重学生认知的差异融合共通促进思维发展
以六年级上册《分数乘法》一课的前测为例。前测题目:3 个的和是多少?列式计算出结果,并把自己的思考过程表达清楚。
师:你们已经把自己的想法写出来了,现在我们就在小组里互相先交流一下自己的想法。
师:我们来看看这些算式对不对?

师:看来是跟以前一样,不管是几个相同的整数、小数、分数相加都可以用乘法来表示。

师:同样想到画图解决,还有些同学是这样表示的,你知道他是怎样思考的吗?
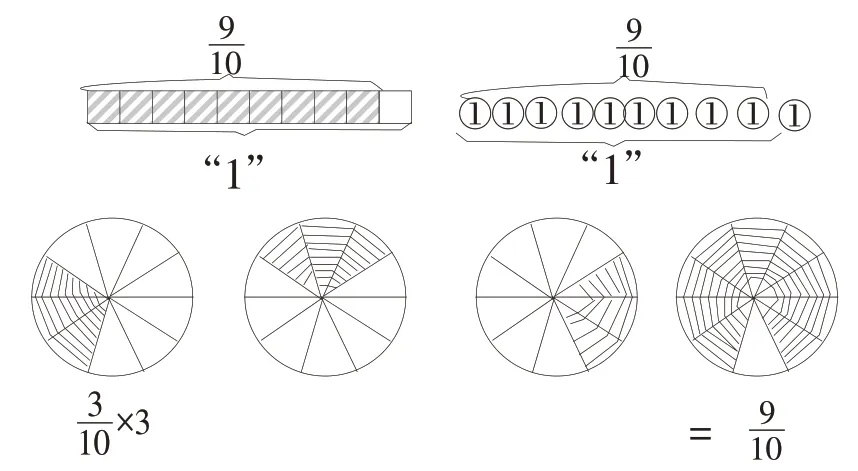
生:我觉的这三幅图结果都是正确的,但不如刚才同学的线段图好。这里第一、二幅图中,看不出是3×第三幅看不出是同一个单位“1”。
师:通过他的介绍,现在你对这几幅图一定有更深刻的认识了吧!我们再来看看大家还想到了哪些方法

生1:①号作品利用乘法的意义就解决了。
生2:②号作品是把分数化小数,利用小数加法解决。
生3:后面两幅作品都是将分数赋予情境来解决的。
师:代到实际情境来解决也不错,你们有没有这样的方法?大家能想到这么多不同的方法,但不同方法之间有没有共同点呢?
生1:都可以用以前学过的方法来解决。
生2:都可以用图来表示。
生3:可以化成统一的分数单位或计数单位进行计算。
……
不同学生能力水平或许不同,但却不一定妨碍他们解决问题。前测中,学生可视化的思维方式很多,课堂教学中,将学生多元性思维充分展现出来,将抽象分数乘整数与直观的图形联系起来,使抽象思维和形象思维结合起来,通过对图形的处理,发挥直观对抽象的支柱作用,从而帮助学生理解分数乘整数运算。
