基于地磁测姿的误差建模及仿真分析*

刘宗源，高 敏，宋卫东，吴汉洲，张 磊

（陆军工程大学石家庄校区，石家庄 050003）

0 引言

对于简易制导弹药，弹箭的滚转姿态信息是实现修正控制至关重要的参数［1］。由于简易制导弹药的安装空间有限、高转速旋转运动，滚转姿态无法利用弹载仪器直接测量。通常利用地磁测量弹丸姿态，利用坐标转化的方法进行姿态解算。随着地磁测姿技术的不断发展，利用地磁传感器测量高速旋转弹丸滚转姿态的研究已经取得了丰硕的成果［2-4］。

地磁场是地球自然形成的覆盖全球的弱磁场，随时间的变化十分缓慢，一般视为恒定量。但由于地磁场强度很小，在地磁数据采集过程中，容易受到传感器自身误差、环境磁干扰弹体剩磁以及内部线圈感生磁场等干扰磁场能够激励地磁传感器模块输出信号。对地磁数据进行误差建模和数据处理已经成为国内外研究的热门之一，文献［5］针对数据的误差较大的问题，介绍了一种基于利用最佳优化思想的数据处理方法，但存在计算复杂及响应速度慢的问题。文献［6］针对数据的椭圆修正和零点化处理进行了研究，提出利用地磁探测弹丸滚转角，但未对数据采集过程中的自身误差和随机噪声进行处理。

本文建立了完整的地磁误差模型，首先采取批处理自适应算法处理随机噪声，再运用MATLAB 自带函数polyfit 进行了椭圆方程的拟合，结合标准地磁数据求得补偿参数，进而消除磁干扰。该方法提高了数据处理的精度和收敛速度，实现了真实地磁信息的还原。

1 误差源分析及模型建立

在实际测量过程中，影响地磁数据精确度的因素主要由自身误差和环境磁干扰组成。其中，自身误差由传感器的自身特性引起，可分为灵敏度误差、非正交误差以及温漂误差。环境磁干扰由弹体及电气线路磁干扰和环境电磁场产生［7］，可分为硬磁干扰、软磁干扰及随机噪声。对数据中的误差、干扰进行建模是数据处理的前提，从中提取出真实的地磁信息是保证姿态解算精度的重要手段。

1.1 自身误差模型

三轴地磁传感器固连在引信上，与弹体进行同样的姿态运动，测量并输出地磁信号。地磁场为弱磁场约为0.5 高斯，需要进行放大才能使用。当三轴地磁传感器的灵敏度和放大电路增益不同时，会使输出值产生误差，一般采用增益矩阵对该误差进行补偿，形式如下：

式中，Kx、Ky、Kz分别为三轴灵敏度系数。

图1 地磁传感器安装示意图

传感器在制造和安装过程中，3 个敏感轴的角度误差会引入非正交误差。ox 轴为弹轴，oy 垂直于ox 指向上方，oz 轴根据右手法则垂直于xoy 平面指向右。

3 个地磁传感器安装在修正引信内部的坐标轴上，假设其中一个地磁传感器安装在z'轴上，z'轴在yoz 平面内与y 轴不垂直，z 轴与z'轴夹角为θ1，如图2 所示。

图2 一种非正交情况示意图

则非正交误差矩阵通过下式表示：

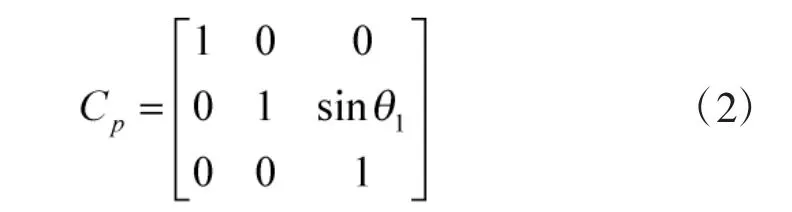
由于元器件的参数变化和环境温度变化形成零点漂移，会产生不同的零位误差，即在参比工作条件下，传感器输出不为0。可用零位误差矩阵表示，形式如下：

零点误差公式：

式中，δppm为电阻温度系数，δT为温度变化量。

因此，该误差模型为：

式中，HB2为地磁输出数据，Cp为非正交误差矩阵，KF为增益矩阵，δF为零位误差矩阵。

该误差模型的参数是可测量的，通过建立的误差模型可以得出补偿参数，因此，相应的补偿相对简单，可直接在传感器输出数据上进行补偿。

1.2 环境磁干扰模型

弹丸在半实物仿真中，地磁数据会受到弹体剩磁、环境电磁场、仪器噪声等环境噪声的影响［8］。实际飞行条件下，弹体以小攻角进行运动，弹轴方向的传感器数据仅有微小变化。为了便于数据分析，可以将弹轴方向的传感器数据假设为一恒定值，然后将赤道面的两组地磁传感器的数据，作为同一坐标系的x 轴、y 轴坐标输入。理论应得到一个圆心位于原点的标准圆，其半径为地磁在弹体赤道面的分量在x、y 轴的投影。但是，实际测量的结果是一个中心不在圆心的椭圆，说明数据受到了硬磁干扰和软磁干扰。

弹体的部分结构由铁磁性材料制成，在地磁传感器工作时，主要以硬磁干扰的形式产生误差。硬磁干扰的大小和方向是恒定的，不随环境改变，对椭圆轨迹的影响是使圆心产生移动。软磁干扰主要由电路磁感应和环境磁干扰产生，通常其强度与环境磁场呈线性关系。软磁干扰的作用是改变椭圆的长短轴比例，对于两种磁干扰，可通过建立校正矩阵进行补偿。

软磁误差系数：

硬磁误差系数：

磁干扰误差模型：

综合上述，最终得出地磁误差模型：

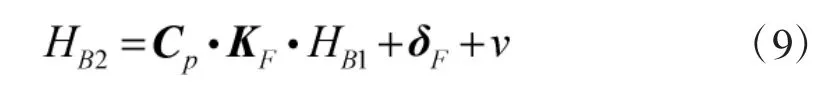
式中，HB2为地磁误差模型，HB1为引入硬磁、软磁误差的数据，v 为随机量测噪声。

该误差模型能够表示环境磁干扰对实测数据的影响，但补偿矩阵的确定比较困难，因此，下文采用椭圆参数补偿方法。

2 滤波及补偿方法

2.1 随机噪声处理

在进行半实物仿真实验时，通常采用高速电机进行弹体旋转运动的模拟。在高速电机正常工作时，转速达到12 000 r/min，产生的振动以随机噪声的形式影响传感器的数据采集。通常利用扩展卡尔曼滤波方法对其进行消除［9］，但是需要利用弹道方程建立状态方程，计算量大，过程复杂，不利于系统的快速响应。传统的数字滤波器FIR、IIR 可以处理与目标信号不同频率的噪声信号，但会产生延迟和频移，需要进行补偿处理，并且难以区分频率类似真实信号的噪声。自适应滤波器是时变非线性系统，参数随输入信号的变化而变化，通过减小与目标信号的均方误差，能够有效处理由环境变化带来的噪声。

图3 实验用高速电机

弹丸飞行过程中传感器的误差系数受外界条件的影响也会发生变化，考虑设计一个参数可调的滤波器。由于采集的数据量非常大，为了便于快速处理，选择工程上常用的批处理自适应（BLMS）算法，其流程如下：

1）给定输入信号x（n），期望地磁信号d（n），对数据进行分批处理：

其中，K 为组标号，L 为数据分批长度。

2）运用滤波公式处理得到输出：

3）计算估计误差公式：

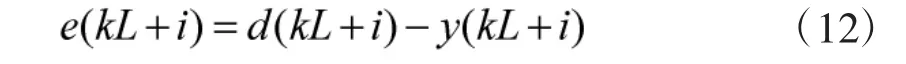
4）滤波系数更新：

式中，σ 为批处理步长因子。

该滤波器通过对输入信号和期望值的处理，不断减小其均方误差性能函数：

式中，wopt为最佳滤波器参数，Rxx为输入信号x（n）自相关矩阵，d（n）为期望地磁信号。

2.2 椭圆补偿处理

对经过去噪的数据进行统计，将其中一组数据作为x 轴坐标，另一组数据作为y 轴坐标，由于数据受到自身误差以及环境的磁干扰作用，将得到的点进行连线得到一个椭圆。该椭圆与标准数据的圆相比，圆心平移，半径产生拉伸。利用数据坐标可以求得椭圆的方程：

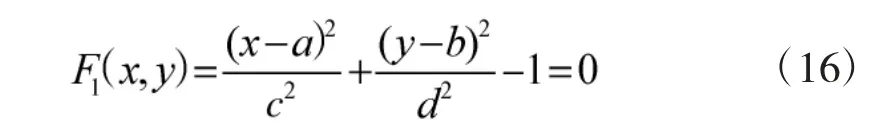
在弹体赤道面上的两个地磁传感器测量的是地磁分量投影，应该为一个标准圆的两轴分量，根据期望值建立标准圆的方程：

可将误差模型简化为：

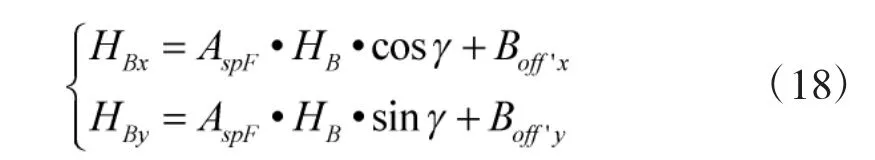
将测量的地磁数据（x0，y0）带入圆方程，得到该点与圆的关系，补偿后地磁数据为：

椭圆补偿因子计算：

1）伸缩因子

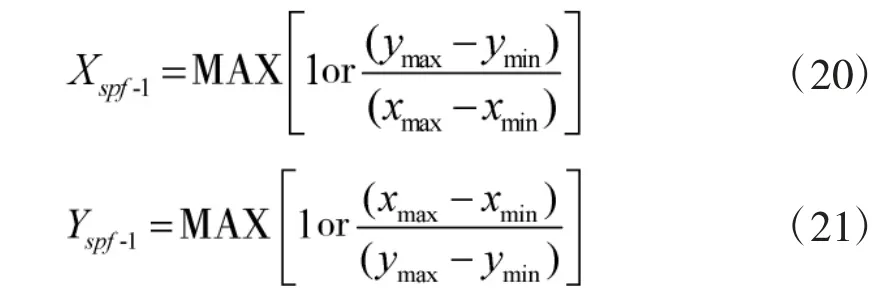
2）平移因子

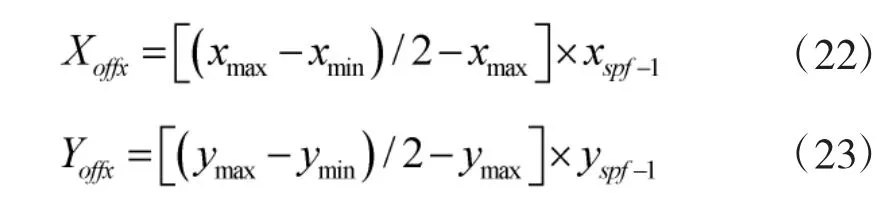
补偿修正值为

式中，δB 是地磁测量值与补偿值的系数，x0是x 轴测量值，y0是y 轴测量值。

3 数据模型仿真分析

为了验证该处理方法的性能，将采集的实验数据按周期进行分组，并将稳定采集后的数据进行均值处理，得到最初的包含误差和噪声的实测数据（假设自身误差在生产环节已经进行了补偿）。首先利用批处理自适应滤波器处理随机误差，对比滤波前后的数据图形，可以看到波形的噪声得到了大幅的衰减。

图4 含噪声的地磁测量值

图5 滤波后的地磁信号

输入噪声信号的方差为150 左右，经过滤波处理后的方差虽然在初期波动较大，但能够很快衰减到50 以下，并随着仿真进行逐渐减小。由此可见该滤波算法能够有效处理实验中的随机误差，满足响应和精度要求。

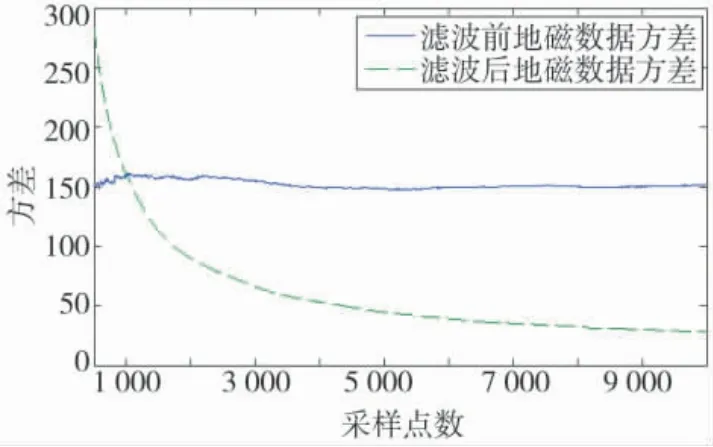
图6 滤波前后数据方程的对比

将消除了随机噪声的数据输入编写的程序，利用程序的运算得出圆心的位移和长短轴。观测输出图像结果，硬磁干扰的影响使圆心偏移至（31.73，67.9），软磁干扰的影响使圆的长短轴比为（38.23∶24.11）。然后根据设计的补偿方法对测量的数据进行修正。图7 中的数据显示了从包含磁干扰的测量数据向标准地磁数据的转化，通过平移伸缩变换对所受的磁干扰进行补偿。通过观察可以得到补偿后的数据圆心修正到了原点，并且接近标准圆。

图7 椭圆补偿处理结果

4 结论

本文针对地磁数据采集精度差、误差源复杂的问题，在系统分析地磁数据误差和噪声模型的基础上，提出了运用BLMS 算法解决数据分批处理问题的方法，搭建了处理实验测量数据的仿真模型。批处理自适应滤波器通过不断调整均方误差性能参数，从而适应环境变化，通过迭代更新使滤波参数达到最优。设计了椭圆补偿方法，通过平移因子、伸缩因子、比例系数的处理拟合标准图形，对传统的椭圆拟合方法进行了简化。仿真结果表明，随机噪声得到了大幅衰减，磁干扰得到了有效补偿，并且避免了传统方法引入的相位偏差，得到最接近真实值的数据。