核心素养视域下小学数学的命题

徐国明

【摘   要】小学数学教学评价应站在发展学生核心素养的时代高度，根据课程目标、课程内容和数学核心素养发展水平，厘定测评内涵，构建测评框架，探索命题策略，从而诊断学与教的优势与不足，帮助改进教学，发展和提升学生的数学核心素养。

【关键词】数学核心素养;命题;策略

书面测验是教学评价的重要形式，能有效考查学生课程目标达成状况，及时反馈教学成效，不断提高教学质量。从“双基”到“四基”，从“两能”到“四能”，再到当下聚焦发展学生的核心素养，书面测验从功能、内容、方式、结果的处理上都需要指向“立足过程，促进素养发展”。

一、对书面测验要求的再审思

新时代背景下的小学数学命题应站在发展学生核心素养时代高度审视课程目标和课程内容要求，以此为基本依据科学构建测评框架、编制试题。

设计试题时，应该关注并且体现课标在设计思路中提出的“十个核心词”，合理设计试题类型，积极探索可以考查学生学习过程的试题，了解学生的学习过程。由此可以看出，课标对书面测验要求注重对数学本质的理解和把握，关注学习过程，体现数学素养发展水平。

基于上述课标对书面测验要求的审视，站在发展核心素养的时代高度进行审视，小学数学命题应体现以下几点：

（一）聚焦数学核心素养阶段水平

小学毕业水平考试命题应体现学生通过小学阶段的数学学习逐步发展形成的数学核心素养水平，特别关注数学学习过程思维品质的形成和关键能力的表现。

（二）突出基础性，注重数学本质

小学毕业年级水平书面测评要注重考查学生对小学阶段重要基础知识与基本技能的理解与掌握程度，及对其中蕴含的数学本质的理解。命题时要体现基础落实，突出内容主线和反映数学本质的基本概念。

（三）关注试题的整体性与灵活性

试题设计要把握小学数学课程的整体目标、内容与数学核心素养阶段的发展水平，灵活设计选择、填空、判断、计算、操作与实践、应用问题等题型，合理布局题量，适度降低计算、操作的难度，淡化解题技巧，适度增加思维含量，更多地关注学生有根有据、有条有理地思考问题。

（四）重视问题的合适情境

素养的测试需要借助情境。在设计试题时，根据评价的目的，赋予问题一定的情境。小学毕业水平考试试题应基于学生熟悉的、具体的情境，考查学生发现、提出数学问题的能力，分析和解决问题的能力，及他们的思维过程和“数学化”水平。要兼顾学生的不同发展水平，可适度设计一定量的开放性或探究性问题。

二、重构书面测评内涵及框架

小学毕业水平考试既要考查学生知识技能的掌握，也要考查数学核心素养水平的达成。在命题上注重考查“四基”“四能”在教学中落实的情况，注重对学科核心知识、数学思维过程的考查，以期通过这样的考查评价为导向，促进教师将数学核心素养落实于教学中。

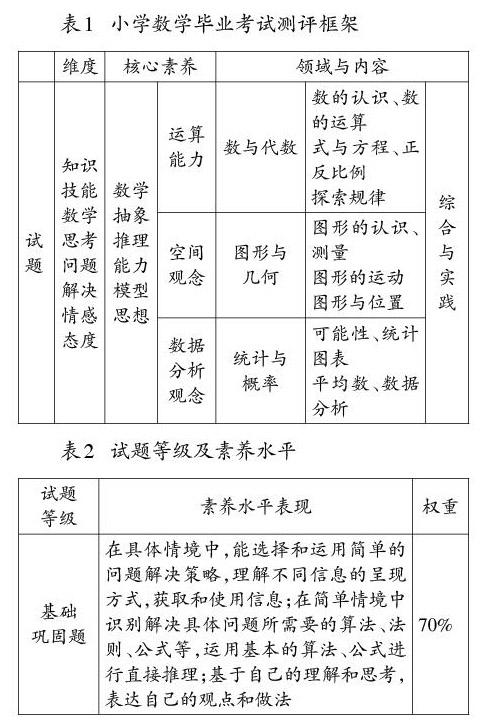
“课标”从知识技能、数学思考、问题解决、情感态度四个方面阐述了教学目标，重视学生从实际背景中抽象出数学问题、构建数学模型，寻求解答、解决问题的过程，这自然就成了命题的维度与命题的内容。结合小学阶段数学课程各内容领域的比重，构建以下的测评框架（见表1）。

基于发展核心素养的小学毕业年级的数学测试题要关注内容与难度的分布、数学核心素养的比重与水平的分布。为了使测试题的难度及评判上更加合理、有效，对试题的等级及所占百分比可作如下规定（见表2）。

三、命题策略与样题举例

一份好的试卷要能检测出学生的数学素养发展水平，发挥评价和导向功能，所以试题命制是一项理论性和技术性很强的工作，近两年笔者一直在积极探索与实践。

（一）依据课标

评价要以“课标”为依据，准确把握小学阶段数学课程的阶段目标、具体内容和要求，设计试题时应符合和体现课标要求。

题1（基础），一袋食盐的标准净重为500g，质监人员为了解每袋食盐净重与标准的误差，把净重502g记作+2g，如果一袋食盐净重498g，记作（        ）;一袋食盐记作-4g，这袋食盐净重（        ）。

題1中学生需要知道以500g为“分界点”，高于它为正，相反的方向则用负数表示，第一空侧重考查学生“用负数表示不足标准的量”，第二空侧重考查学生对“负数表示的实际量”的了解。此题考查学生能否灵活运用正、负数表示生活中具有相反意义的量，及对正、负数所表示实际含义的理解。这样的设计，符合课标对负数这一内容的要求，即“在熟悉的生活情境中，了解负数的意义，会用负数表示日常生活中一些量”。

（二）基于教材

以教材为本，用好教材，把教材内容教好，把教材问题解决好，把教材任务落实好，是实现课程目标的基础性工作。因此，基于教材是试题命制的基本策略。可对教材中的概念、例题、习题，通过适当改变呈现形式、拓展延伸空间，考查学生对基本概念、重点知识的理解和掌握情况。在命题中，力求试题能从课本中找到题目的“原型”，把教师教学导向放在对教材的深度解读、把握教学内容的本质上。

题2基于教材例题中通过直观图理解算理和习题中看图计算改编而来。学生通过观察比较，发现从左图到右图变化的联系，以算式表征图意，数形结合，以考查学生对几何直观的感知能力，对分数乘法算理的理解和掌握情况。

（三）外显思维

在评价中不仅要关注学生对知识技能的掌握程度，还要关注学生的思维过程。命题时，要为学生提供开放表达的机会，促使学生基于理解进行个性化的表达，留下思维的痕迹，外显思考的过程。

题3（灵活），下面长方形表示2平方米，请在长方形中画方格、涂颜色（或用不同的线条）表示长方形左边的分数。

分数是小学阶段的基本概念之一，它既可表示倍比关系，也可表示具体的数量。题3借助直观的图形将学生的思维过程外显。画左图时，“这个长方形表示2平方米，看作单位‘1，将其平均分成5份，再涂出其中的2份，也就表示出2平方米的[25]”的思考过程自然地外显。画右图时，学生既可以将这个表示2平方米的长方形平均分成5份，涂出其中1份，反映出学生将“[25]平方米理解为表示2平方米的[15]”的思考过程;也可以先将这个表示2平方米的长方形平均分成2份，再将其中1份平均分成5份，涂出其中2份，反映出学生将“[25]平方米理解为表示1平方米的[25]”的思考过程。如此这样，既考查了学生对数学概念本质的理解，更考查了学生的思考过程。

（四）贴近生活

命题时以学生熟悉的日常生活、学习生活为素材创编试题，可考查学生综合应用数学知识解决实际问题的能力。

题4（综合），六（2）班某次数学测验成绩的统计图表损坏了（如下图），请利用图表中仅存的数据信息解答下列各题。

① 该班一共有（   ）人参加了测验。

② 该班这次数学测验成绩的“优秀率”是（   ）。

③ 已知“良好”与“合格”人数之比为7∶9，那么得“良好”等级的有（   ）人。

④ 测验时，如果班上一个同学因病请假。第二天数学老师让这位同学进行了补考，这位同学考了94分，那么，这个班数学测验的平均分约（   ）（填提高或降低）（   ）分。

题4以学生数学测验为素材。解决这一问题，需要对统计图表的数据认真进行观察分析，发现数据背后隐藏的信息及内在关联，综合应用百分数（百分率）、比、平均数的知识分别解答问题。在综合运用这些知识解决问题过程中，既考查了学生对相关数学概念的理解，也考查了学生综合应用知识解决问题的能力，体现了对学生的数据分析观念、数感、运算能力、推理能力等数学核心素养发展水平的考查。

（五）有時代感

试题具有时代色彩，可以近几年国内外发生的大事件或取得的科学技术新成就为素材，融知识性、时代性、人文性于一体。

题5（基础），四川是人口大省，据第六次全国人口普查统计，四川省常住人口有八千零四十万八千二百人，写作（              ）人，四舍五入到万位约是（             ）人。

题5以第六次全国人口普查为背景，考查学生对大数的认识情况，也对学生进行了省情、国情教育，增强社会责任感。

评价是落实“核心素养”培养的重要保障。教师应聚焦数学核心素养，依据其内涵、价值、行为表现，积极探索构建基于发展核心素养测试的评价框架，科学编制试题，以期通过对测试结果的定量分析，诊断学生的学习过程与教师的教学过程的优势和不足，进而改进教学，促进学生数学核心素养的提升。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]孔凡哲.面对以核心素养为本的评价，一线教师可以做些什么[J].小学教学，2017（2下）.

[3]苏明强.核心素养视角下的小学数学教学[J]. 教育视界， 2016（34）.

[4]林国忠，徐国裕.基于教材的命题策略研究[J].教育评论，2017（8）.

（四川省峨眉山市教师培训中心  614200）