行波效应对不同结构体系多塔斜拉桥地震响应影响
——以杭州湾六塔斜拉桥(嘉绍大桥)为研究案例
2019-11-05方自奋
方自奋
(厦门合道工程设计集团土建一院 福建厦门 361004)
0 引言
近年来,大跨度桥梁在全世界范围内越来越流行,其建设发展也极为迅速,关于大跨度桥梁结构的抗震研究受到日益广泛的重视。在目前的大跨度桥梁实际工程中,地震分析中地震输入方法通常采用一致激励法,但是对于地面支承距离大、延伸长的大跨度桥梁,尤其是大跨度多塔多点地面支承的多塔斜拉桥结构,地震动的空间变化的影响不容忽视。在地震反应分析中必须考虑多支承点的不同激励,即多点激励问题[1-5]。因此,本文建立了不同机制地震激励下大跨度斜拉桥的地震反应分析方法,以杭州湾的六塔斜拉桥-嘉绍大桥为例,数值仿真了不同结构体系多塔斜拉桥在确定性地震波一致激励以及考虑行波激励的多点激励下的地震反应,分析了行波效应对大跨度多塔斜拉桥地震反应的影响。
1 基本理论
1.1 基本方程
假令所研究的结构模型受到外界环境干扰力F(t)的作用,则其结构系统的运动方程可表示为[6-7]。
(1)
式中M、K和C分别为结构质量、刚度和阻尼矩阵;Ds为环境干扰位置矩阵。
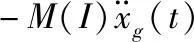
(2)
但是,通过相对加速度输入模型中来实现地震激励的方法并不适用于多点激励响应分析,多点激励响应分析需要直接对绝对位移或绝对加速度输入模型直接求解,而现有的有限元软件通常无法直接实现各支承点的非一致激励响应分析,需要重新进行编程分析,而自编程序耗时耗力,通用性差,难以实现[8]。为此,人们基于有限元软件的现有功能,提出了基于有限元绝对加速度及位移输入模型的实现方法。根据实现方式的不同,该方法可以分为大质量法、大刚度法以及绝对位移输入法。本文拟采用大质量法(LMM)来模拟多点激励地震效应。
1.2 大质量法
大质量法,是基于加速度时程输入模式的方法,其基本思想为:在地面各支承节点处赋予其远大于模型总质量的大质量(至少大于模型总质量的10倍),使得底部支承点的惯性力响应占总响应的大部分;再对底部支承点在地震输入自由度方向释放边界约束,这样大质量支承节点与整体模型之间通过主从约束成为一个变形整体;最后在支承节点上沿地震输入自由度方向施加力的时程[9]。
此方法通过对于支承点施加外力,使支承大质量产生振动,实现各支承点的多点激励效应,表达式如下:
(3)
式中,
Mz、Cz及Kz分别为支承节点处质量、刚度及阻尼;
Ms、Cs及Ks分别为结构除支承节点以外质量矩阵、刚度矩阵及阻尼矩阵;
Mbig为所赋予支承节点上的大质量;
Fb(t)为支承节点上所施加的力时程;

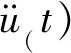

大质量法在求解方程中,并不涉及到位移的分解,可以通过直接积分方法求解得到结构整体地震响应,同时也十分适用于非线性分析。为此,本文采用此方法模拟多点激励地震效应。
2 数值模拟
2.1 背景工程
浙江嘉绍大桥由绍兴市上虞起,跨越钱塘江水域至嘉兴市海宁[10],总重量达4×105t,采用还是比较典型的斜拉桥设计方案,为六塔独柱四索面钢箱梁斜拉桥,主桥由连续的五跨六塔斜拉桥组成,每跨428m,宽度为55.6m,全桥长度为10.137km,结构形式为2个三塔一联对称结构,联与联之间由一抽屉型刚性铰相连接,桥跨跨径布置为70+200+5×428+200+70m。桥梁设计基准期为100年,抗震设防烈度为6度,场地土类别为Ⅳ类。嘉绍大桥布置详图如图1所示。

图1 嘉绍大桥结构布置详图(单位cm)
2.2 有限元模型
本文分析所采用的有限元基准模型,是基于在ANSYS有限元软件平台的基础上建立。如图2所示,对于嘉绍大桥的闭口薄壁截面钢箱梁桥面系,采用beam4单元脊骨梁模型模拟;对于桥塔与桥墩,则是采用考虑剪切变形的铁木辛柯梁beam189来模拟;对于斜拉索,采用空间桁架link10单元来模拟;对于结构的影响效应,则是采用Penzien质量-弹簧模型模拟;在2个三塔一联对称结构中相连接跨中,设置2个梁端点主从约束来模拟抽屉型刚性铰。
结构模型除桥塔底部与地面约束条件之外,主梁与过渡墩、辅助墩横向、竖向及绕纵向扭转主从约束,其余自由度相对自由;刚性铰处,仅释放相对纵向平移自由度;主梁与主塔之间,横向、竖向主从约束。主梁与主塔在不同结构体系下,关于纵向自由度的约束条件分别为:基准体系:次边塔(2塔、5塔)与主梁纵向主从约束,其余塔与主梁释放纵向约束;全固接体系:主塔与主梁纵向主从约束;全漂浮体系:主塔与主梁释放纵向约束。
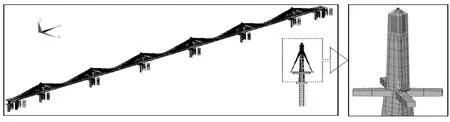
图2 嘉绍大桥有限元模型
2.3 地震波选取
基于ANSYS有限元软件平台,建立嘉绍大桥基准模型,然后根据嘉绍大桥桥址的地质条件,在太平洋地震研究中心选取3条适宜的地震波,并将此3条地震波加速度时程曲线峰值调为0.1392g,表1为所选取3条地震波初始参数,图3为加速度峰值调为0.1392g的3条地震波加速度时程曲线。

表1 选取地震波参数
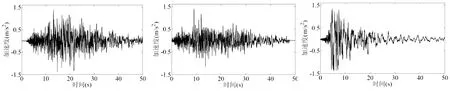
(a)DZ1 (b)DZ2 (c)DZ3图3 地震波加速度时程曲线
3 地震响应分析
3.1 主梁地震响应
嘉绍大桥不同结构体系模型在1(纵桥向)+0.65(竖桥向)地震动输入模式中,对于主梁地震响应主要考察部分为:主梁的纵向位移及主梁的竖向位移。本小节在对模型进行基于500m/s、1000m/s及2000m/s地震波剪切波速的多点输入激励及一致输入激励地震作用模拟的基础上,提取了主梁的地震响应进行对比。其中,令方案0为有限元模型一致输入激励下地震响应;方案1为模型基于2000m/s地震波剪切波速的多点输入激励下地震响应;方案2为模型基于1000m/s地震波剪切波速的多点输入激励下地震响应;方案3为模型基于500m/s地震波剪切波速的多点输入激励下地震响应。最终计算结果,以3条地震波计算结果最大值为标准。图4~图6是嘉绍大桥主梁地震响应对比图。

(a)主梁纵向位移幅值 (b)主梁竖向位移幅值图4 基准模型主梁地震响应对比图
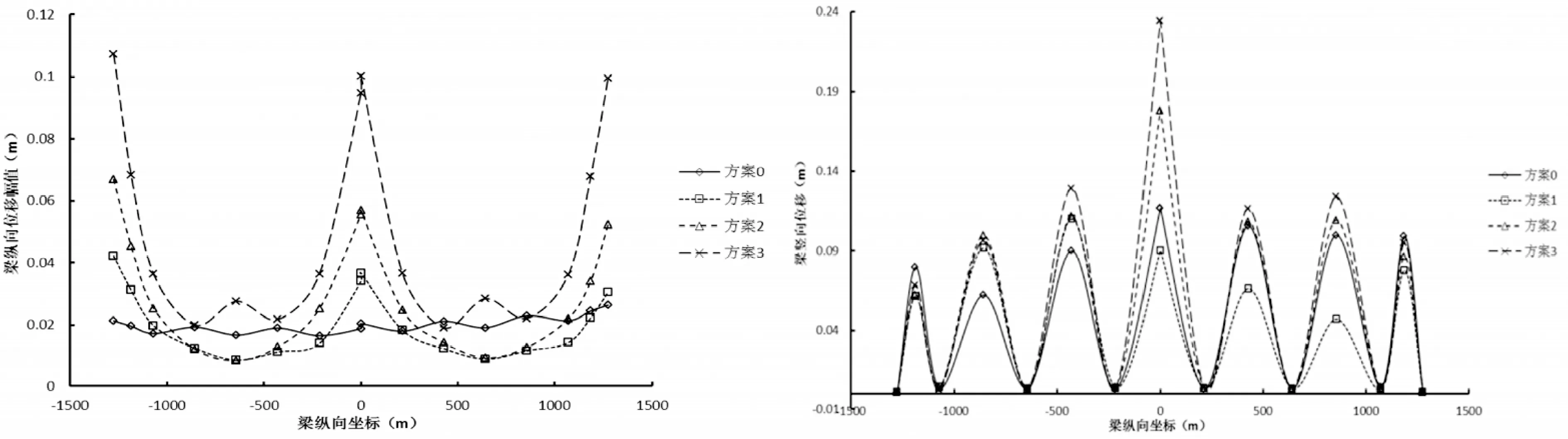
(a)主梁纵向位移幅值 (b)主梁竖向位移幅值图5 全固接模型主梁地震响应对比图

(a)主梁纵向位移幅值 (b)主梁竖向位移幅值图6 全漂浮模型主梁地震响应对比图
由图4~图6可以看出:
(1)考虑行波效应对主梁纵向位移及竖向位移影响特别大,近似地将一致输入激励等效为地震波剪切波速很大的多点输入激励,则发现:随着地震波剪切波速的减少,主梁纵向位移及竖向位移幅值迅速变化,且变化规律差异性较大。如:基准模型中方案0主梁最远端纵向位移幅值为0.037m,方案3主梁最远端纵向位移幅值为0.191m,增大了416%;基准模型中方案0中跨跨中竖向位移幅值为0.117m,方案3中跨跨中竖向位移幅值为0.235m,增大了101%。
(2)针对不同结构体系下主梁的地震响应受行波效应的影响差别十分明显,如:主梁与右侧桥墩连接处的纵向位移在基准模型中,随地震波剪切波速的减少呈上升趋势,而在全漂浮模型中,随地震波剪切波速的减少呈下降趋势。即:行波效应对于主梁地震响应的影响与结构自身约束条件有较大关系。
(3)针对于主梁不同地震响应受行波效应的影响差别十分明显,如:全固接模型中,中跨跨中纵向位移幅值,随地震波剪切波速的减少呈上升趋势,而中跨跨中竖向位移,随地震波剪切波速的减少呈先减少再增大趋势。即:行波效应对于主梁地震响应的影响与所研究的响应类型有较大关系。
3.2 主塔地震响应
嘉绍大桥基准模型,在1(纵桥向)+0.65(竖桥向)地震动输入模式中,对于主塔(墩)地震响应主要考察其桥塔纵桥向内力(剪力、弯矩)、纵向位移及塔(墩)梁结合处相对位移。本小节在对模型进行基于500m/s、1000m/s及2000m/s地震波剪切波速的多点输入激励及一致输入激励地震作用模拟的基础上,提取了主塔的地震响应进行对比。最终计算结果以3条地震波计算结果最大值为标准。图7~图9是嘉绍大桥主塔地震响应对比图。

(a)塔(墩)顶纵向位移幅值 (b)塔(墩)底纵向剪力幅值
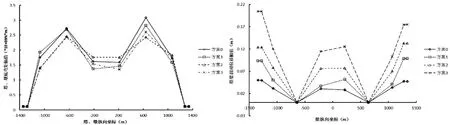
(c)塔(墩)底纵向弯矩幅值 (d)塔(墩)梁结合处相对位移幅值图7 基准模型塔(墩)地震响应对比
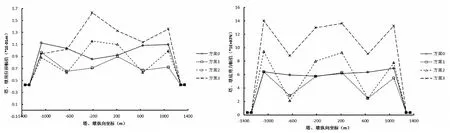
(a)塔(墩)顶纵向位移幅值 (b)塔(墩)底纵向剪力幅值

(c)塔(墩)底纵向弯矩幅值 (d)塔(墩)梁结合处相对位移幅值图8 全固接模型塔(墩)地震响应对比

(a)塔(墩)顶纵向位移幅值 (b)塔(墩)底纵向剪力幅值

(c)塔(墩)底纵向弯矩幅值 (d)塔(墩)梁结合处相对位移幅值图9 全漂浮模型塔(墩)地震响应对比
由图7~图9可以看出:
(1)考虑行波效应对主塔纵向内力(剪力、弯矩)、纵向位移及塔(墩)梁结合处相对位移影响较大,近似地将一致输入激励等效为地震波剪切波速很大的多点输入激励,则发现:随着地震波剪切波速的减少,主塔的地震响应迅速变化,且变化规律差异性较大。如:基准模型中方案0的3塔塔顶纵向位移幅值为0.093m,方案3的3塔塔顶纵向位移幅值为0.150m,增大了38%;基准模型中方案0的2塔塔底纵向剪力幅值为6.90e+4kN,方案3的2塔塔底纵向剪力幅值为5.76e+4kN,减少了17%;基准模型中方案0的5塔塔底纵向弯矩幅值为3.09e+6kN·m,方案3的5塔塔底纵向弯矩幅值为2.60e+6kN·m,减少了16%;基准模型中方案0的右侧桥墩墩梁结合处相对位移为0.047m,方案3的右侧桥墩墩梁结合处相对位移为0.175m,增大了298%。
(2)针对于不同结构体系下主塔的地震响应受行波效应的影响差别十分明显。如:3塔塔顶纵向位移在基准模型中,随地震波剪切波速的减少呈先下降后上升趋势;而在全漂浮模型中随地震波剪切波速的减少呈下降趋势。即:行波效应对于主塔地震响应的影响与结构自身约束条件有较大关系。
(3)针对于主塔不同地震响应受行波效应的影响差别十分明显。如:全漂浮模型中,3塔塔底纵向剪力幅值随地震波剪切波速的减少呈先上升后下降再上升趋势;而3塔塔底纵向弯矩幅值随地震波剪切波速的减少呈先下降趋势。即:行波效应对于主塔地震响应的影响与所研究的响应类型有较大关系。
(4)各桥墩在地震输入下的地震响应(纵向位移、纵向内力)基本一样,且考虑行波效应对于桥墩的地震响应几乎没有影响,这是由于桥墩在纵向自由度上类似于独立悬臂梁结构。
4 结论
本文以连接杭州湾的第二座跨海大桥-嘉绍大桥为研究对象,数值仿真了不同结构体系多塔斜拉桥在确定性地震波一致激励以及考虑行波激励的多点激励下的地震反应,分析了行波效应大跨度多塔斜拉桥地震反应的影响,结论如下:
(1)与一致激励计算结果相比,考虑地震动的行波效应后,结构位移及内力响应有显著影响,且行波效应对结构响应的影响不是单一的,对部分结构内力可能是有利的,但对另外一部分可能是不利的。
(2)在基准模型中,对于主梁地震响应而言,行波效应影响较为显著,主梁位移幅值增大可达400%,竖向位移部分增达100%。即:同一结构的不同响应,如内力及位移,影响程度及规律不尽相同。
(3)针对于不同结构体系下,随着地震波剪切波速的减少,主梁与主塔地震响应的变化规律差异性十分明显。即:行波效应对于桥梁地震响应的影响与结构自身约束条件、视波速、构件位置有较大关系。
(4)行波效应对嘉绍大桥的地震响应影响不可忽视,对嘉绍大桥等大跨度多塔斜拉桥进行地震模拟分析时,应考虑行波效应的影响。
