拟人腕关节机构的动载协调分配优化
2019-11-05李研彪罗怡沁徐梦茹
李研彪 王 林 罗怡沁 徐梦茹 郑 航
1.浙江工业大学机械工程学院,杭州,3100232.浙江工业大学特种装备制造与先进加工技术教育部重点实验室,杭州,310023
0 引言
并联机构具有结构紧凑、工作空间大、承载能力强等优点,广泛用于拟人关节机构[1-4]。目前,拟人腕关节机构有轮系机构[5]、5R正交机构[6]、3RRR机构[7]、3UPU机构[8]等,但拟人腕关节机构的原型仍较少。笔者拓展一种3UPS/S并联机构,并将其作为拟人腕关节的机构原型。
并联机构在运动过程中需要克服重力、外力、惯性力等负载,并将这些负载合理地分配到各个驱动器,以实现动载协调分配的优化[9]。将不同因素作为优化目标,最终可以得到不同的分配方式,国内外学者对此进行了大量研究。徐桂玲[10]以驱动力最小为目标,应用虚位移原理和加权最小二乘法,对四足并联腿步行机器人进行优化;卿建喜等[11]、窦玉超等[12]通过优化驱动力、驱动功率来降低瞬时负载和瞬时功率;余联庆等[13]采用伪逆法来最小化瞬时驱动力的二范数,从而减小最大瞬时驱动力。上述并联机构均将驱动力或功率作为优化目标进行动载分配。单一考虑驱动力、功率时,机构可能存在运动速度、加速度等的突变,从而导致机构运动的不平稳。
有学者通过规划运动轨迹来实现动载分配。如LIU等[14]考虑驱动速度、加速度和驱动力的限制,采用多项式样条的方式来构建3RRRU并联机构的运动轨迹,从而求解出最优的运动时间。CHEN等[15]考虑驱动速度、加速度和驱动力,采用遗传算法对6SPS并联机构进行轨迹规划,使机构的能耗最低。KHOUKHI等[16]、GUILBERT等[17]提出了一种新的并行多目标轨迹规划方法,使并联机构实现低能耗的运动。上述优化方法从时间、能耗角度进行求解,但并没有考虑机构驱动器的输出情况,导致规划的轨迹存在驱动力较大、突变等问题。
本文研究拟人腕关节机构的动载协调分配问题,采用Dijkstra算法得到机构综合性能最优的运动轨迹,并综合考虑时间、能耗、平稳性,采用遗传算法优化求解广义时间,从而使机构在时间短、能耗低和性能优的条件下完成运动。
1 机构介绍
本文研究的拟人腕关节将3-UPS/S并联机构作为机构原型,如图1所示。该机构由动平台、定平台、3条UPS/S驱动支链和球铰支架组成。球铰支架固定在定平台上,通过球铰与动平台连接。球铰支架约束动平台的3个移动自由度,使动平台只有3个转动自由度。3条UPS/S驱动支链中,电缸为机构的驱动器(包括摆动轴和伸缩轴),电缸的下端通过虎克铰连接定平台,电缸的上端通过球铰连接动平台。3个球铰中心在半径r1的圆上均布,3个虎克铰中心在半径r2的圆上均布,动平台和定平台的距离为r3。

1.定平台 2.电缸 3.球铰 4.动平台5.中央球铰 6.球铰支架 7.虎克铰图1 拟人腕关节机构的模型Fig.1 Model of humanoid wrist joint mechanism


图2 拟人腕关节机构简图Fig.2 Schematic diagram of humanoid wrist joint mechanism
定坐标系{A}与动坐标系{B}重合时,动平台处于初始状态。构建摆动轴局部坐标系Uixciycizci和伸缩轴局部坐标系Dixdiydizdi,分别记作{Ci}和{Di},其中i=1,2,3。坐标系{Ci}的坐标原点与虎克铰的旋转中心Ui重合,坐标系{Di}的坐标原点与伸缩轴的质心Di重合,且zci轴和zdi轴沿着支链伸缩方向,yci轴和ybi轴垂直于OSiUi平面,根据右手定则确定xci轴和xdi轴。
2 运动学建模
2.1 位置反解
采用Z-Y-X型欧拉角描述腕关节的动平台姿态,则动平台的姿态旋转矩阵为
(1)
cj=cosjsj=sinjj=α,β,γ
在定坐标系{A}上,虎克铰和球铰的中心点Ui、Si的位置矢量为
(2)
ηi=5π/3-2iπ/3i=1,2,3
根据腕关节的结构特点,可得支链i驱动方向的矢量
li=Si-Ui
(3)
则腕关节的驱动支链i的长度为
(4)
2.2 速度反解
(5)
则球铰中心点Si的速度为
(6)
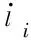
对式(6)两侧点乘ei,可得支链驱动线速度
(7)
对式(6)两侧叉乘ei,可得支链角速度
ωi=ei×(ωh×Si)/li
(8)
式(8)的矩阵形式为
(9)
E3=diag(1,1,1)
3 动力学建模
机构中的连接件不会对运动产生影响,故将其视为邻近连杆的一部分。同时,为便于动力学建模,忽略各运动副之间的摩擦力,将各连杆和动平台皆视为均质刚体,并考虑惯性力、外力和重力对机构的作用。
3.1 惯性力求解
采用拉格朗日方法,从能量的角度来计算惯性力。
3.1.1系统动能
系统动能包括摆动轴动能、伸缩轴动能和动平台动能。摆动轴绕虎克铰的旋转中心Ui转动,其动能为
(10)
(11)
(12)
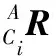
伸缩轴运动包括绕虎克铰的旋转中心Ui的转动和沿伸缩方向上的移动,故其动能包括平动动能和转动动能:
(13)
(14)
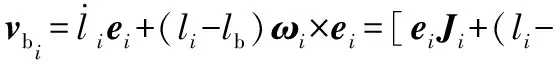
(15)
式中,AIbi为支链i上的伸缩轴相对于过质心的坐标系的惯量矩阵;vbi为支链i上球铰中心Si的速度;mb为伸缩轴的质量;Ib为伸缩轴绕坐标系{Di}的主转动惯量;lb为伸缩轴质心到球铰中心的距离;Ji为雅可比矩阵J的第i行向量;S(ei)为ei的反对称矩阵。
由于动平台始终绕中央球铰的旋转中心O转动,故动平台的动能为
(16)
(17)
式中,Ih为动平台相对于动坐标系{B}的主转动惯量。
结合式(10)、式(13)和式(16)可得系统动能:
(18)
3.1.2系统势能
在定坐标系{A}中,取Oxaya面为重力零势能面,重力方向为za轴的反方向。由于动平台的质心与旋转中心O重合,且动平台始终绕旋转中心O转动,因此动平台势能为零。系统势能包括摆动轴势能和伸缩轴势能:
(19)
式中,zai、zbi分别为摆动轴和伸缩轴质心在定坐标系{A}中Z轴方向的坐标值。
3.1.3广义惯性力
根据朗格朗日方程可得
(20)
L=E-Vψ=[γβα]T
式中,FI为对应广义坐标ψ的广义惯性力。
将式(18)、式(19)代入式(20)整理可得
(21)


矩阵D为对称的广义惯量矩阵,除受构件的质量和分布影响外,还与雅可比矩阵有关。矩阵H、C分别表示系统的离心力和哥氏力,均与机构姿态有关,U为重力项。
3.2 外力求解
由于动平台始终绕旋转中心O转动,因此当外力和外力矩作用在动平台上的任意位置时,均可以等效成作用在旋转中心O上的外力和外力矩。因为作用在旋转中心O的外力对驱动力大小无影响,所以广义外力只需要考虑作用在旋转中心O的外力矩。动平台的外力分解模型如图3所示。

图3 动平台外力分解模型Fig.3 External decomposition model of moving platform
设作用在动平台任意位置上的外力Fg=[FM]T,则广义外力为
Ff=M+F×d
(22)
F=(Fx,Fy,Fz)M=(Mx,My,Mz)
式中,d为Fg到旋转中心O的矢量。
3.3 动力学模型建立
综合考虑重力、惯性力和外力作用,建立腕关节的动力学模型:
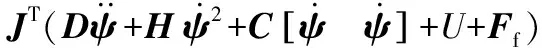
(23)
其中,τ=[τ1τ2τ3]T为3个驱动器对应的驱动力;JT为力雅可比矩阵,将广义坐标系上的驱动力转换到各驱动器上。
3.4 数值算例及模型验证
腕关节机构的参数如表1所示。承受外力F=0,M=[1 1 1]TN·m。基于上述动力学模型,利用MATLAB软件计算得到腕关节机构的关节驱动力矩曲线。为了验证动力学模型的正确性,利用动力学仿真软件ADAMS对腕关节机构进行动力学仿真。添加各类约束条件和外力,使仿真与理论计算的环境保持一致。将仿真得到的关节驱动力与理论计算得到的关机驱动力进行比较,并分析仿真结果与理论结果之间的误差,如图4所示。由图4可知,驱动力的仿真值与理论值的误差在1%左右,基本一致,验证了动力学模型的正确性。

表1 腕关节机构的参数
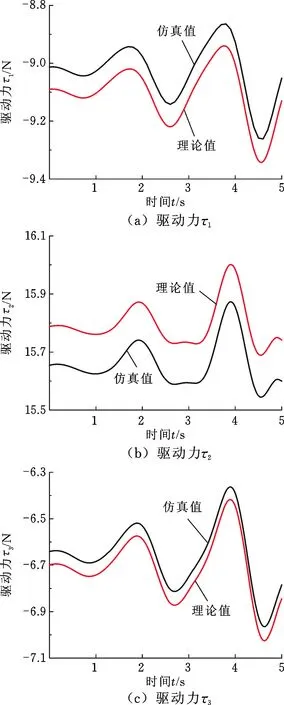
图4 关节驱动力理论值与仿真值Fig.4 Theoretical and simulated values of joint drive force
4 腕关节机构的性能分析
4.1 动力学性能评价指标
由式(21)可知,腕关节机构不同的运动状态会影响惯性力,其中,速度、加速度直接影响机构惯性力的大小。腕关节机构一般做低速运动,因此忽略速度影响,只考虑加速度的影响,则式(21)可简化为
(24)
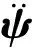
(25)
对式(25)求偏导,可得
(26)
化简式(26)可得
(27)
式中,λ为矩阵DTD的特征值。
由式(27)可知,λ随机构姿态变化而变化,λ越小,由加速度引起的惯性力越小。

4.2 力映射性能评价指标
将式(23)化简可得
τ=JTτF
(28)
式中,τF为广义坐标系上的广义惯性力、重力和外力之和,称为广义驱动力。
由式(28)可知,通过虚功原理可将广义坐标系上的驱动力映射到各驱动器上。其中,力的雅可比矩阵JT代表该映射关系。
由于rankJ=3,故力雅可比矩阵JT可以奇异值分解,存在正交阵U∈R3×3和V∈R3×3使
JT=UΛV=Udiag(σ1,σ2,σ3)V
(29)
式中,σi(i=1,2,3)为力雅可比矩阵JT的奇异值且σ1≥σ2≥σ3。
设广义驱动力τF为单位向量,可得
τTU(ΛΛT)-1UTτ=1
(30)
当广义驱动力τF为单位矩阵时,关节驱动力矩分布在椭球上;σi越大,广义驱动力转换为驱动力的效率越高,因此将k3(k3=σ3)作为力传递性能评价指标,k3越大,力传递性能越好。
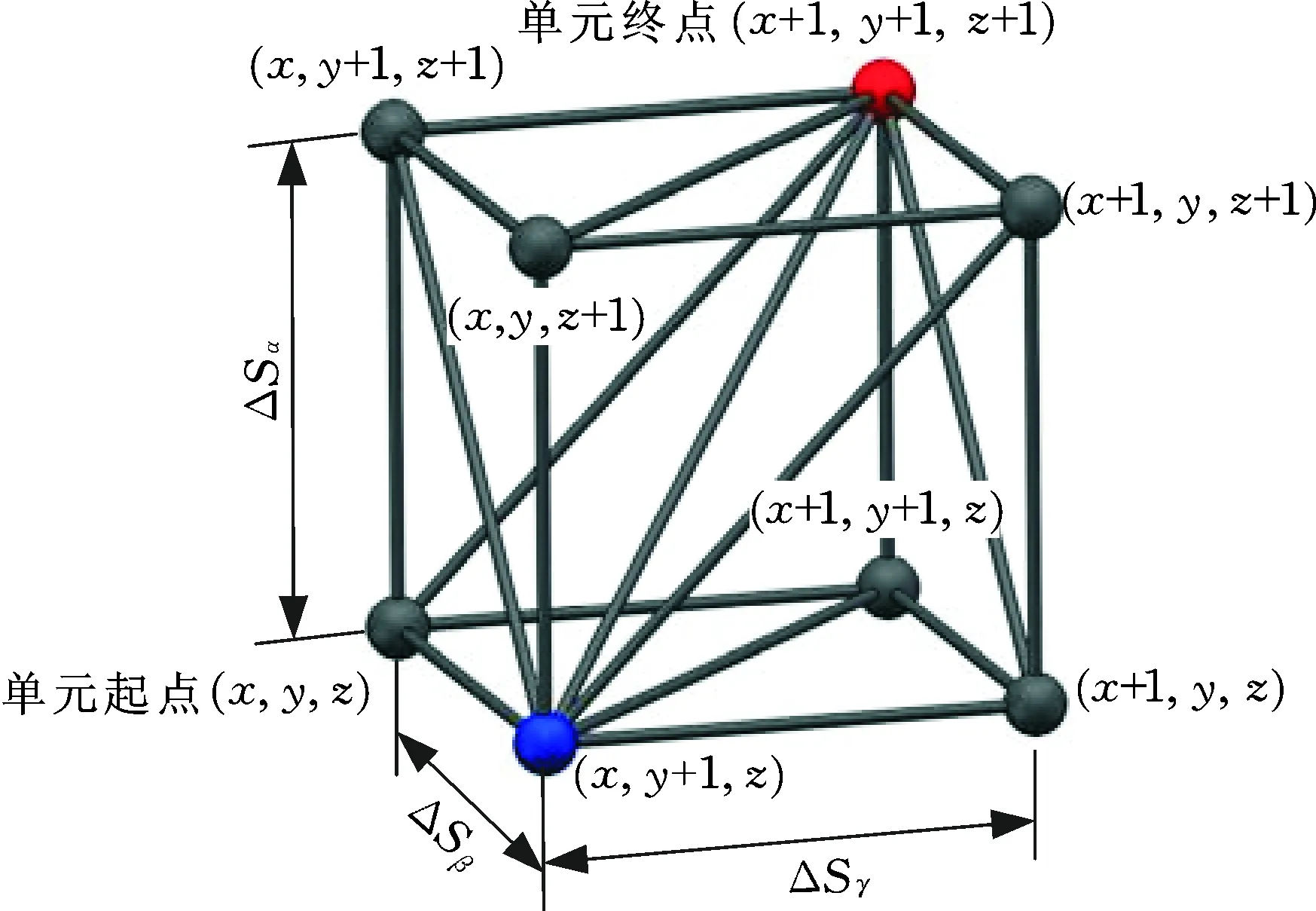
σ1=σ2=σ3时,驱动力分布在空间球上,驱动力之间的差值最小,因此将k4(k4=σ3/σ1且0 本文考虑时间、能耗、性能,依据性能指标得到性能最优的轨迹,通过遗传算法优化求解最优广义时间,从而使腕关节机构在能耗最低、时间最短、性能最好的情况下完成运动。 综合考虑动力学性能(动力学传递性能和动力学传递均衡性能)和力映射性能(力传递性能和力传递均衡性能)因素,采用加权求和法,将上述多性能指标转换成综合性能指标。 求解出各性能指标在全域范围内的最大值kjmax和最小值kjmin(j=1,2,3,4),则不同姿态下的各性能指标可表示为 (31) 式中,Kj为性能指标在全域变换范围内的比值。 Ki越大,机构性能越好。 综合考虑上述4个性能指标的影响,构造综合性能指标函数 (32) 式中,δj为目标比重系数。 δj越大,该衡量指标越重要,本文中的δj=1,各性能指标的比重相同。K越小,机构的综合性能越好。 设腕关节机构姿态起点ψ0=[γ0β0α0]T,姿态终点ψt=[γtβtαt]T。腕关节机构从起点出发运动到终点有许多不同的路径。将起点至终点的区域进行离散,以不同的离散点组合来表示不同的路径,则离散步长为 (33) 式中,ΔSγ、ΔSβ、ΔSα分别为欧拉坐标γ、β、α的离散步长;n1、n2、n2为离散的步数。 将每一个离散点根据其位置关系进行标记,如图5所示。由图5可知,每一个单元存在单元起点和单元终点。根据单元标记规则,可以构建从起点至终点的路径网格。网格内的每个离散点存在一个表示某种姿态下机构的综合性能指标K,将K定义为该离散点的权值。将路径上所有离散点的综合性能指标K的和,表示该条路径的综合性能。路径综合性能指标越小,该路径的综合性能越好。 图5 离散单元标记规则Fig.5 Discrete cell marking rule 离散单元的路径规则如图6所示。离散点从单元起点出发,到达单元终点,且不存在返回的现象。从起点到终点的离散点构成了一条路径。路径上的离散点越少,该路径越短。 图6 离散单元路径规则Fig.6 Discrete cell path rule 给定姿态起点ψ0=(0, 0, 0),姿态终点ψt=(π/18, π/18, 5π/36)。以路径最短、综合性能最好为目标,采用Dijkstra算法优化求解出从起点到终点的最优路径,算法流程如图7所示。 图7 Dijkstra算法流程图Fig.7 Dijkstra algorithm flow chart 由于规划出的路径为一系列离散点,无法实现光滑轨迹运动,故基于上述性能最优路径的结果,采用B样条曲线拟合方法构造动平台运动轨迹,即可得从起点至终点的最优轨迹,并利用多项式函数来描述,则最优轨迹方程如下 (34) 式中,u为路径中离散点的序号,u=0,1,…,8。 腕关节机构的最优路径和最优轨迹如图8所示,最优轨迹沿着最优路径分布,且避免了最优路径不光滑的缺点,确保了运动的平稳性。 图8 拟合轨迹Fig.8 Fitting trace 由最优轨迹方程(式(34))可知,动平台的运动轨迹与参数u有关。建立参数u与时间t的函数,确定腕关节机构的速度特性。采用多项式方程建立的时间函数为 u(t)=a0+a1t+a2t2+a3t3+a4t4 (35) 式中,a0~a4为时间函数的系数。 5.2.1约束条件 已知腕关节机构的起点和终点的位置,且起点和终点的速度为零,故建立时间约束方程 (36) 式中,T为运动时间。 同时,驱动器输出的速度和力存在最大值,故建立驱动器输出约束方程 (37) 5.2.2目标函数 设腕关节机构在时间T内完成运动。腕关节机构在运动过程中可能存在时间很短、能耗很大或关节力矩变化很大的情况,因此,需要考虑能耗和关节力矩。建立能耗优化目标和力矩波动优化目标: (38) (39) 考虑时间、能耗、稳定性,结合式(38)、式(39),建立广义时间优化目标函数 (40) 其中,λ1、λ2为目标值所占的比重,λ1=λ2=0.5,将能耗和力矩波动视为同等重要。 优化过程如下:首先根据式(34)、式(35)计算出动平台的角位移和角速度,其次根据腕关节位置、速度反解方程求解关节驱动器的输出值,然后根据动力学模型得到关节驱动力矩,最后通过式(40)得到广义时间优化目标函数。采用遗传算法对式(35)时间函数中的系数ai和运动时间T进行优化求解,如图9所示,得到最小的广义时间f。 图9 广义时间遗传算法流程图Fig.9 Genetic algorithm flowchart of generalized time 广义时间的优化结果如图10所示。由图10可知,运算结果收敛,得到优化结果如下:时间T=1.4 s,时间函数系数a0=a1=0,a2=16.05,a3=-11.26,a4=1.94。 图10 广义时间优化结果Fig.10 Generalized time optimization result 将上述得到的优化结果代入式(35)得到时间函数,并根据腕关节机构的位置反解、速度反解和动力学模型,通过MATLAB计算得到优化后的驱动力、驱动位移和驱动速度。 如图11~图13所示,腕关节机构的驱动力、驱动位移和驱动速度的曲线均光滑,不存在突变,说明优化后的机构能够实现平稳运动。在起止时刻,驱动速度均为零,符合实际运动状况。3个驱动力和驱动速度均处于同一数量级,数值大小接近,说明该优化方法能够把机构惯性力和外力合理地分配到3个驱动器上。 图11 腕关节机构的驱动力Fig.11 Drive force of wrist joint mechanism 图12 腕关节机构的驱动位移Fig.12 Drive displacement of the wrist joint mechanism 图13 腕关节机构的驱动速度Fig.13 Drive velocity of the wrist joint mechanism 定义各驱动器输出功率的绝对值在时间轴上的积分为能耗。在相同时间下,腕关节沿着不同的轨迹完成运动,分别计算腕关节机构优化前后的能耗,如图14所示。优化后,腕关节机构的能耗降幅为39.53%,验证了该动载协调分配优化方法的可行性。 图14 耗能对比图Fig.14 Comparison diagram of energy consumption (1)考虑外力、重力和惯性力的作用,结合拉格朗日方法和虚功原理,建立了腕关节机构的动力学模型。利用ADMAS进行动力学仿真,理论数值与仿真数值的误差在1%左右,验证了动力学模型的正确性。 (2)基于动力学模型,推导了腕关节机构的动力学性能评价指标和力映射性能评价指标,采用加权求和法得到了综合性能指标,利用Dijkstra算法得到了综合性能最优的运动轨迹。 (3)基于综合性能最优的运动轨迹,考虑时间、能耗、平稳性,建立了广义时间优化目标函数,并采用遗传算法求解得到最优广义时间。数值算例表明:优化后机构运动能耗降低了39.53%,验证了该优化方法的可行性。5 动载协调分配优化
5.1 综合性能最优路径
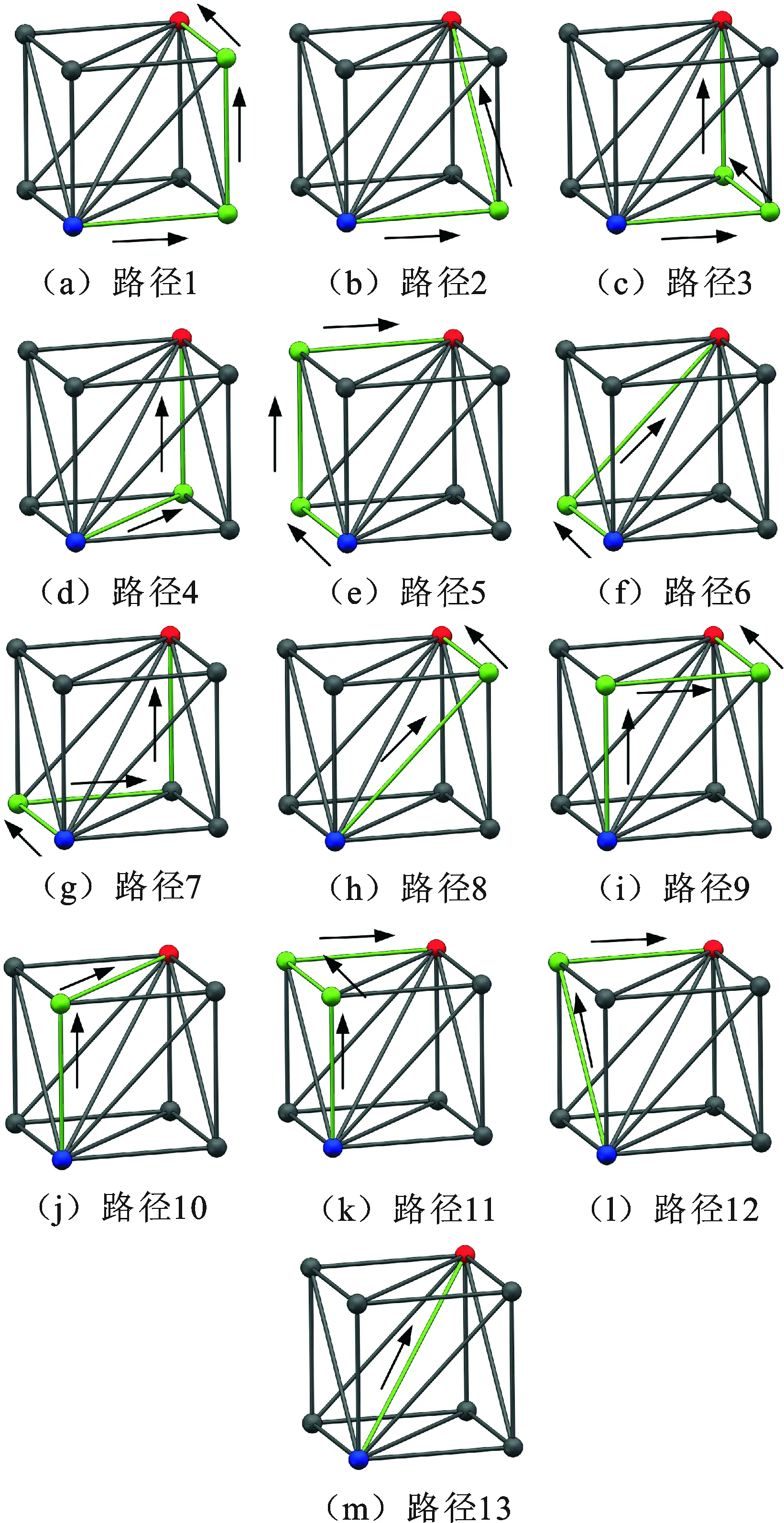

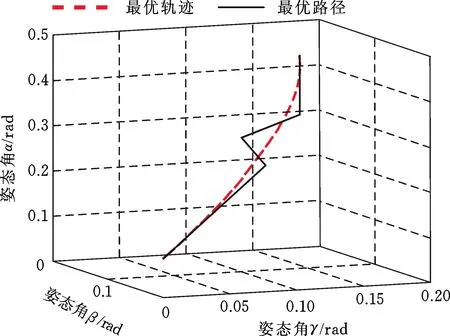
5.2 约束条件及目标函数建立
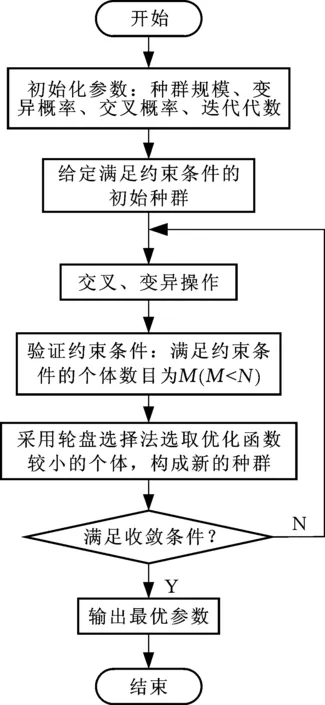
5.3 广义时间优化

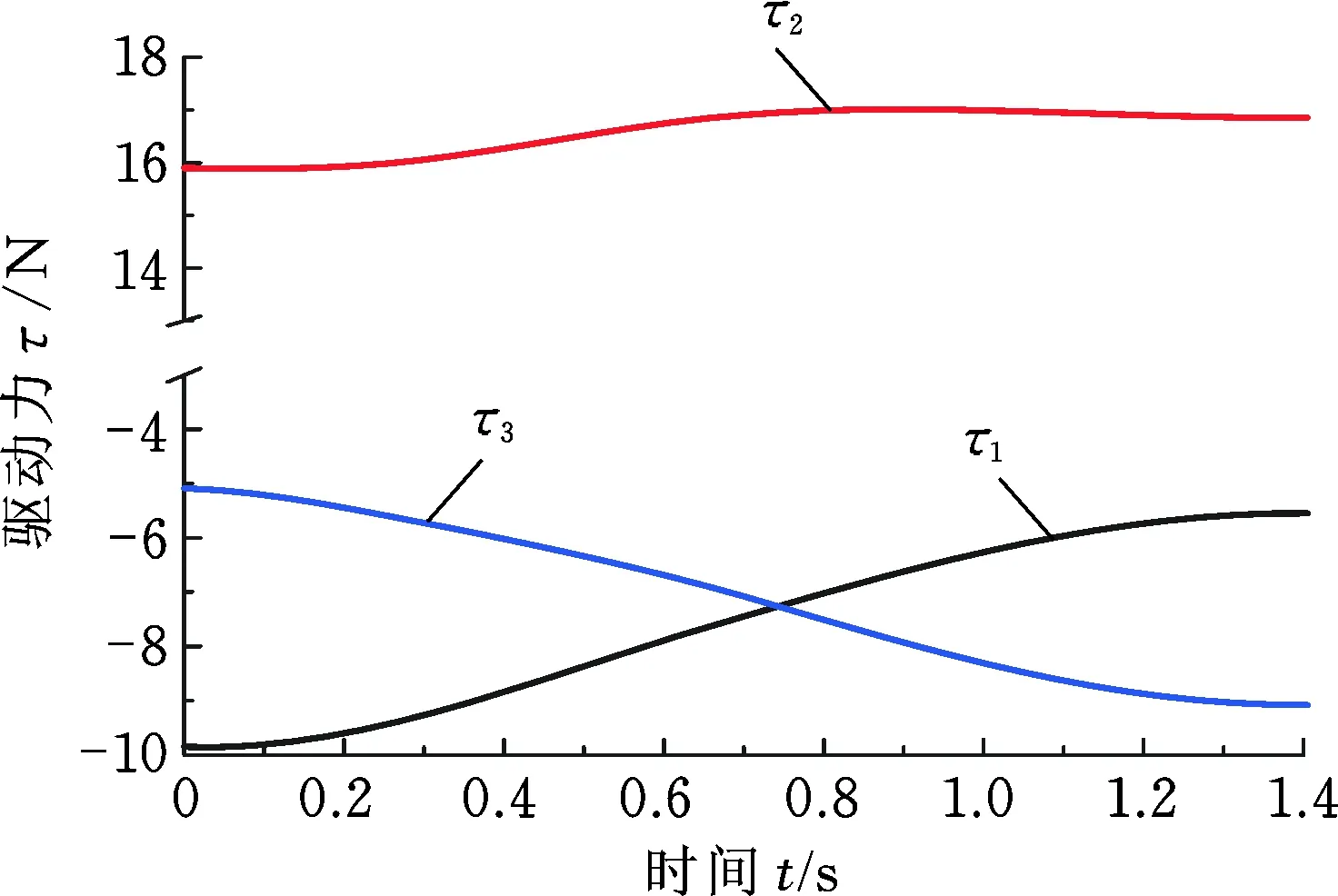
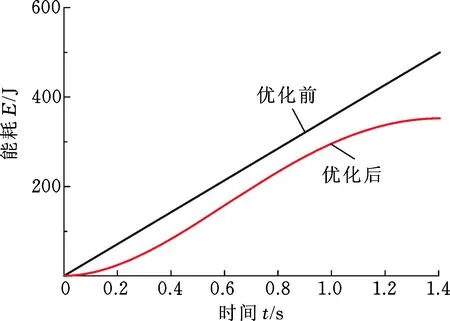
5.4 优化结果分析


6 结论
