球形机器人动力学建模与运动控制设计

曾 鹏，张启伦，张 超，郑功倍，高丙团

（1.贵州电网有限责任公司 电力科学研究院，贵阳550002；2.贵州电网有限责任公司 兴义安龙供电局，安龙552400；3.贵州创星电力科学研究院有限责任公司，贵阳550002；4.东南大学 电气工程学院，南京210096）

电缆通道的工作环境恶劣，采用移动传感网络进行状态监测可以有效地提供工作效率、保障人员安全。球形机器人是一款综合了足式和轮式机器人特点的移动机器人，其具有“不倒翁”的特性，不会轻易发生倾覆，环境适应能力较强，且密闭的球形外壳可有效地保护球内的监测传感元件，可以作为电缆通道移动传感网络移动节点[1-2]。

自20世纪90年代球形机器人问世以来[3]，球形机器人的机构和控制设计受到广泛的关注和研究[4-5]。轮式驱动方式通过在球内放置轮式驱动的小车实现，其结构较为直观，且内部车体便于搭载传感设备，更适合于作为移动网络的传感节点。然而，由于单轮驱动运动轨迹单一，四轮驱动成本较高，故在此选择双轮驱动的球形机器人作为电缆通道移动网络的机器人节点。

当前国内外对双轮驱动移动机器人的研究鲜有报道，其动力学特性和运动控制有待研究。本文针对双轮驱动的球形机器人，首先基于拉格朗日方程法建立其动力学模型；在此基础上，分析球形机器人的转向运动和直线运动特征，从而设计机器人的速度、位置PID 控制器，实现球形机器人的速度和位置闭环运动控制，以满足传感网络节点的运动控制要求。

1 动力学建模

双轮驱动球形机器人如图1所示。图中，均质球壳内部有一两轮独立驱动的小车，静止状态下小车的质心与球心距离为l。在小车上，可以安装电缆通道监测需要的视觉传感设备、 无线通信模块等，通过左右两轮的独立驱动可以实现球形机器人的运动控制。

图1 球形机器人示意图Fig.1 Schematic diagram of spherical robot

球形机器人的相关参数变量设定如下：M 为均质球壳质量；m 为内部小车车体质量；mw为车轮质量；R 为球壳半径；Rw为车轮半径；h 为静止状态下车轮与球壳接触点到球心的竖直距离；d 为左右车轮间距的1/2；θ 为车体质心与球心连线相对于垂直方向的倾角；θL和θR分别为左右车轮滚过的角度；φ为车体前进方向逆时针偏离x 轴正方向的角度；τL为左侧电机输入的驱动转矩；τR为右侧电机输入的驱动转矩。

球形机器人是一个多体系统，运动体包括球壳、内部车体、左右驱动轮，可采用拉格朗日方程建立系统的动力学模型。选择左驱动轮转角θL，右驱动轮转角θR，内置车体倾角θ，球形机器人移动距离S作为广义坐标。基于广义坐标计算系统的动能和势能，车体动能Ek1为

式中：Jm为内部质心到球心的等效转动惯量；Jφm为转向过程中车体相对于曲率圆心的转动惯量。球形机器人转向角速度与车轮驱动速度的关系为

车体势能Ep1为（设球壳中心点为零势能点）

2 个车轮动能Ek2为

式中：Jw为车轮相对于车轮轴的转动惯量。2 个车轮的势能Ep2为

球壳动能Ek3为

式中：JM为球壳相对球心的转动惯量；JφM为转向过程中球壳相对于曲率圆心的转动惯量。球壳势能Ep3=0。

由此可得到球形机器人的拉格朗日函数为

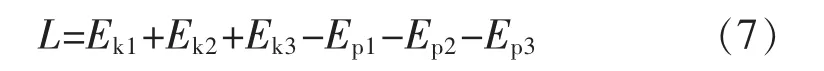
系统耗散能量主要由小车摆动过程中的黏性阻尼引起，则可定义为

式中：ξ 为黏滞阻尼系数。

在计算广义力的过程中，考虑左、右车轮与球壳之间的摩擦力FL和FR，球壳与地面之间的摩擦力Ff，分别定义为

式中：μ1和μ2为摩擦系数；sgn（·）为符号函数。则相对应的广义力分别为

其中

式（12）～式（15）即为两轮驱动球形机器人的动力学模型。由动力学模型可以看出系统是复杂非线性的，且只有2 个直接驱动控制输入τL和τR，但要控制系统的广义坐标构型变量有4 个，因此系统是欠驱动的。

2 运动控制设计

球形机器人在作为移动无线传感器网络移动节点时，根据不同控制需求（如单独移动还是编队移动）需要控制其速度或者位置。PID 控制具有结构简单、稳定性好、鲁棒性强等特点，在实践中广泛采用。PID 控制可根据需要，由比例P（proportion）、积分I（integration）、微分D（differentiation）这3 个单元组合成不同的控制器。在此采用PID 控制实现对球形机器人速度与位置的控制。

球形机器人的移动速度和驱动轮转动速度之间的关系为

结合式（2），可得球形机器人运动轨迹的曲率半径为

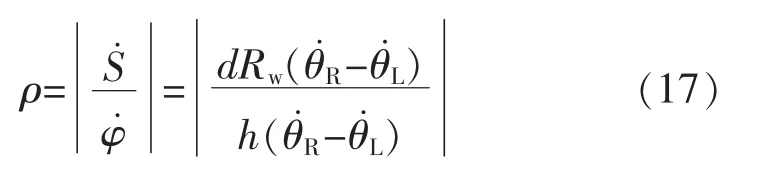
由式（17）可知，当2 个驱动轮的速度大小相等但方向相反时，转向半径ρ=0，说明双轮驱动的球形机器人可实现零半径转向，即原地转向；当2 个驱动轮的速度大小和方向均相同时，曲率半径无穷大，即做直线运动。因此，针对不同方向上的速度或者位置控制要求，可分解为一系列的原地转向和直线运动控制。鉴于此，在直行运动的情况下，设计的PID 控制方案如图2所示，可实现对球形机器人运动速度的控制。

图2 PID 控制系统框图Fig.2 PID control system block diagram

在速度控制的过程主要关心速度控制的稳定性和控制精度，根据PID 控制设计经验，可采用PI控制实现，将期望速度与实时速度的偏差项作为输入，控制输出设计为

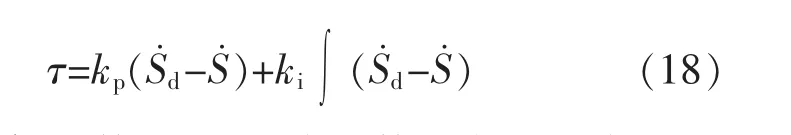
式中：kp为比例系数；ki为积分系数。考虑到实际驱动电机提供的力矩存在上限，对控制器输出的控制量进行限幅处理，并通过调节矩阵将控制输出转矩分为2 个同值分别驱动2 个驱动轮。

当球形机器人需要移动到某平面位置时，根据上述分析可知，可通过球形机器人原地转向和直线运动组合完成。基于前述的速度PI 控制器设计，根据经典速度位置双闭环设计思想[7-8]，类似的设计如式（18）所示的位置闭环PI 控制器。控制器设计与速度PID 控制器相似，输入量为期望路程与实时路程的偏差项，输出量同样经过限幅处理后，通过调节矩阵得到球形机器人的控制转矩，再输入至系统。机器人原地转向运动时，通过调节矩阵将控制输出转矩分为2 个相反数，分别驱动2 个驱动轮实现转向控制。

3 仿真分析

3.1 开环动力学仿真

在MatLab/Simulink 2018B 中，根据式（12）～式（15）搭建球形机器人的模型，通过直线运动和转弯运动2 组仿真试验来建立的动力学模型进行验证。

模型中所涉及的固定参数数值如下：M=0.05 kg，m=0.3 kg，mw=0.005 kg，R=0.08 m，Rw=0.02 m，l=0.06 m，h=0.048 m，d=0.064 m，g=9.8 m/s2。仿真中初始状态均设为0。

首先，验证球形机器人动力学模型的开环直行运动，设τL=τR=0.05 N·m，仿真时长8 s。仿真结果如图3所示。由图可见，球形机器人从初始位置开始，沿着φ=0 的方向直线运动，由于驱动轮质量较小且考虑了摩擦力，驱动轮在恒定力矩的作用下其速度在较短的时间内达到匀速，车体倾角在过渡过程结束后保持恒定，球形机器人能够实现匀速的直线运动控制，与预期一致。

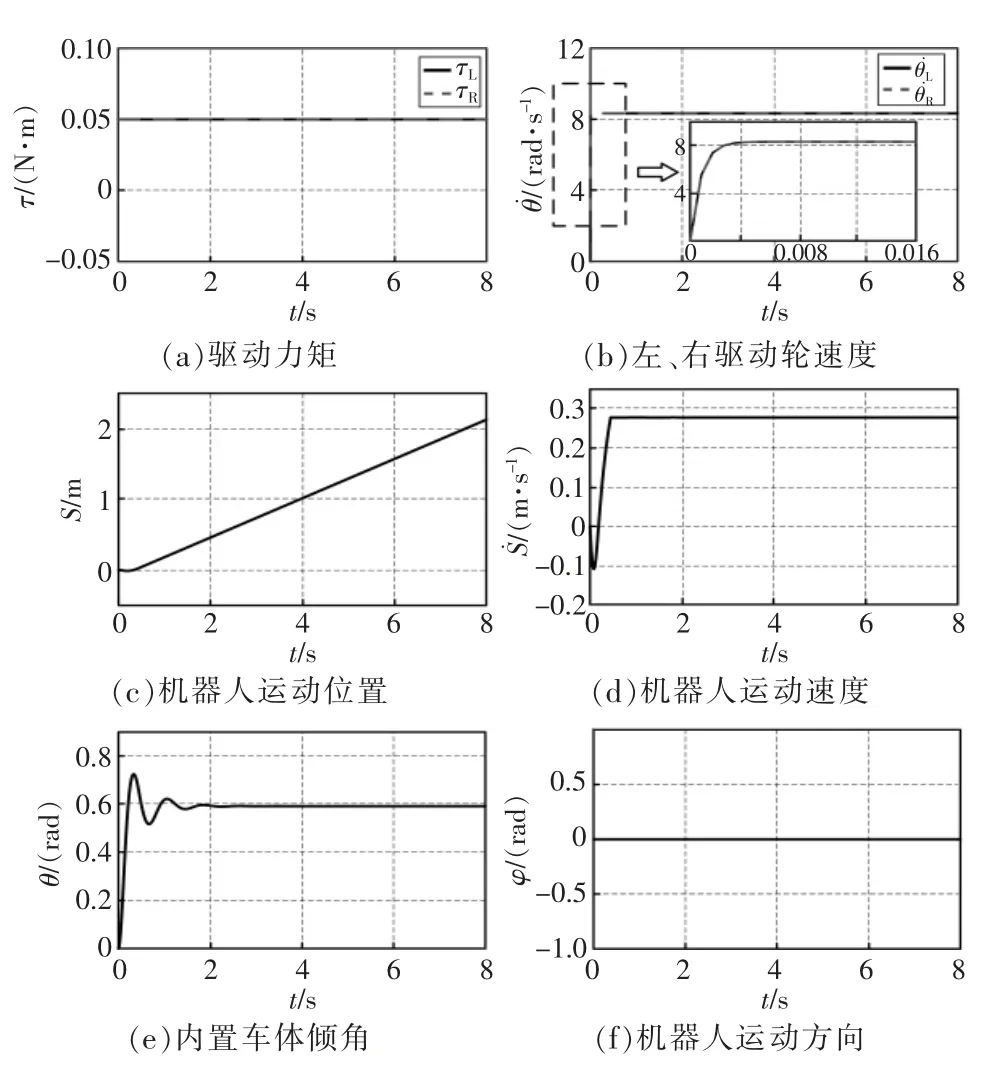
图3 开环直线运动仿真结果Fig.3 Simulation result of open loop control for linear motion

进一步验证球形机器人的转向运动试验。设置3 组不同的输入转矩：τL1=-0.04 N·m，τR1=0.04 N·m；τL2=0 N·m，τR2=0.04 N·m；τL3=0.04 N·m，τR3=-0.02 N·m。各状态量的初值均为0，仿真结果如图4所示。

图4 开环转向运动仿真结果Fig.4 Simulation result of open loop control for steering motion

由图4所示轨迹可见，在原地静止状态下，开环输入左、右驱动轮不同的转矩得到不同转向半径的运动轨迹，输入转矩左右轮差值的正负产生不同的转向方向，差值的大小产生不同的转向半径。当左右轮输入转矩大小相同方向相反时，原地转向，轨迹为一个点，即初始位置点。这符合上述分析和实际的直观经验，表明了球形机器人动力学模型的合理性和正确性。

3.2 闭环运动控制仿真

3.2.1 闭环的速度控制仿真

根据动力学模型的仿真结果，虽然开环控制可以实现球形机器人的匀速直线运动，但控制转矩与速度的关系不明确，且开环系统鲁棒性较差。

仿真中，设置各状态量的初值均为0，运动速度的期望值S˙d=0.2 m/s，比例系数kp=0.14，积分系数ki=0.5，控制器输出量的幅值限制为0.07 N·m。将限幅处理后的输出量经调解矩阵得到球形机器人的控制转矩，输出至系统并进行仿真，试验结果如图5所示。

图5 速度控制仿真结果Fig.5 Simulation of speed control

由图可见，约t=2 s 时速度以达到期望值，车体姿态角在速度稳定后还存在一定的振荡，在恒输出转矩作用下由黏滞摩擦的作用自动实现车体姿态角的稳定调节；在t=3 s 时系统达到稳定。此后，球形机器人保持稳定状态的匀速直线运动，证明了所设计速度PI 控制的有效性。

3.2.2 目标位置闭环控制仿真

进行球形机器人的目标位置闭环控制仿真，在初始状态均为零的情况下，设定向φ=π/4 方向行走S=0.3 m，角度控制PI 参数分别为0.15 和0.3，仿真结果如图6所示。

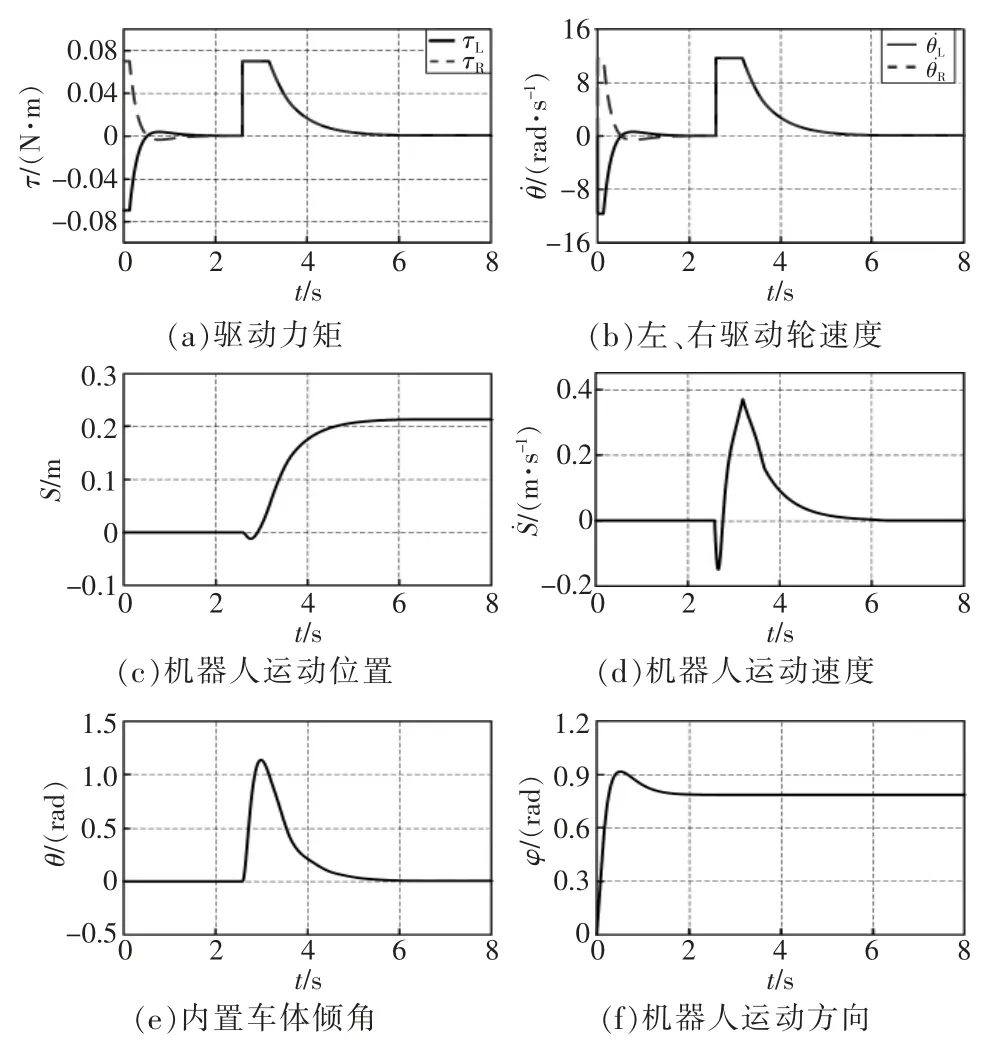
图6 位置控制仿真结果Fig.6 Simulation of position control

运动控制过程分为2 个步骤，先进行原地转向调节，再进行直线位置移动。由图6所示仿真曲线可见，首先输出左右驱动轮方向相反大小相同的控制转矩进行原地转向，经过约2.5 s 的时间球形机器人完成原地转向控制，在2.5 s 之内小车位移为0 且保持不变。调整好方向后，小车运动方向角保持恒定的期望值，输出方向和大小均相同的左右轮驱动转矩开始直线移动，经过约3.5 s 的时间，路程达到期望值，此后机器人静止，完成精确的位置控制，实现闭环位置控制的目标。

4 结语

结构简单、成本低廉的双轮驱动球形移动机器人，作为电缆通道等危险恶劣环境移动无线网络监测系统节点的有力候选，需要首先掌握其动力学并进行运动控制设计。在此，采用拉格朗日方程法，建立了完整的双轮小车驱动的球形机器人动力学模型；采用易于实现的PI 控制器，设计了系统的速度和位置闭环控制系统。通过将不同位置的运动控制分解为原地转向和直线运动，进一步简化了控制实现。仿真试验分别验证了所建立的动力学模型和设计的闭环运动控制方案，证明了动力学模型和控制方案的正确性和可行性。论文的研究成果可以为下一步组建电缆通道移动无线传感监测网，奠定部分工作基础。