基于迭代无迹卡尔曼滤波的无人机编队协同导航

唐大全，邓伟栋，唐管政，鹿珂珂，陈 正

（1.海军航空大学，烟台264001；2.中国人民解放军91967 部队，褡裢054100）

随着科技的不断进步，无人机技术发展十分迅速。在军事领域，无人机最早出现于20世纪20年代，在第一次世界大战期间，英国的卡德尔和皮切尔两位将军就提出了无人作战的设想，由此逐渐设计成型，并在伊拉克战争、阿富汗战争以及在阿伯塔巴德突袭等战争活动中发挥了重要作用[1-2]。在民用领域，随着无人机技术的不断成熟，从最早的航拍无人机开始，逐渐应用于电力巡检、交通巡查、快递运输等领域，减轻了人类的负担，提高了工作效率。

当前，无人机作业往往以单架次的形式执行相关活动，随着任务需求和复杂性的不断提高，单架无人机在执行任务过程中具有一定的局限性，这就促进了无人机编队形式的诞生。为确保无人机编队整体效能大于单架无人机效能的累加，要求无人机编队内部之间具有较强的协调一致性、 整体协同性。因此，精确的导航定位性能是进行无人机编队队型设计、航迹规划的基础，也是圆满完成各项任务的重要保证。

1 无人机编队协同导航的算法研究

目前用于编队导航的方式有很多，研究较为深入的有主从式、并行式、平行式协同导航[3]，具体各个编队方式的优缺点也有了较为全面的概括，这里不再赘述；由于协同导航过程是非线性，所以应用较为广泛的算法是在卡尔曼滤波基础上衍生的扩展卡尔曼滤波、无迹卡尔曼滤波以及粒子滤波等滤波算法。

卡尔曼滤波由学者卡尔曼提出，只能用于解决线性系统滤波和预测问题[4]，因为无人机在协同导航过程中的观测方程是非线性的，所以传统的卡尔曼滤波不能解决此类问题。对此，文献[5-8]将卡尔曼滤波算法推广到了非线性领域，并针对性地提出了扩展卡尔曼滤波EKF（extended Kalman filter），其原理是将非线性系统的模型函数进行泰勒展开，并且忽略二阶及以上高阶项，此方法能够较好地解决弱非线性系统方程。但当系统的非线性较强时，如果采用局部线性化处理非线性系统的估计问题，会带来较大的误差，同时在滤波过程中，需要计算系统方程的Jacobian 矩阵，因而增加了滤波计算量。

无迹卡尔曼滤波[9-10]UKF（unscented Kalman filter）以UT（unscented transformation）无损变换为基础，使用卡尔曼滤波框架对非线性系统进行滤波估计，选取一定数量的采样点，利用这些采样点的均值和协方差逼近原非线性系统。与EKF 相比，该方法避免了求解Jacobian 矩阵和海塞矩阵，同时可以使非线性系统精确到二阶泰勒级数，提高滤波精度。

无论是EKF 还是UKF，其本质都是一种近似的估计方法，在给定初始状态的前提下，利用状态方程和观测方程进行估计，得到逼近真实值的最优估计，如果使用更加靠近真实状态的估计值进行滤波更新，会进一步提高近似精度，故在此提出一种迭代卡尔曼滤波算法。该算法以UKF 为基础，通过极大似然函数确定迭代条件，利用Levenberg-Marquardt方法[11]调整预测协方差矩阵，对无人机编队量测环节进行迭代更新，多次用观测更新后的状态估计作为输入，对观测方程再次进行滤波处理，所得的状态估计值更加准确。

2 无人机编队协同导航原理

在已知基准坐标系的初始位置和速度的前提下，惯性导航系统不依赖任何外界信息，同时不向外辐射任何能量，在准确测量载体航行位置的基础上，具有较强的隐蔽性能[12]。但在长时间使用时，会由于误差的积累导致导航定位精度下降。为此，现有的无人机一般采用惯性导航系统INS（inertial navigation system）和全球定位系统GPS（global positioning system）相搭配的导航模型，采用高精度的GPS 对无人机惯导系统进行实时校正，保证定位精度。

一般情况下，无人机编队协同导航方式分为主从式和平行式。在无人机编队系统中，如果每架无人机均配备高精度导航设备，一方面会增加成本，且在战场运用时，容易遭受打击，增加损失。另一方面，无法突出无人机编队的优势，实用性和效能性不高。在此重点研究主从式协同导航，即一台配备高精度定位设备的主无人机，其余无人机配备精度较差的导航定位设备。

在协同定位的过程中，主从无人机首先进行时间校对，确保无人机编队在相同的时间维度下，主无人机按照规定的时间间隔向外发射自身导航信息，从无人机接收到主机精确的导航信息后，与自身导航设备测得的位置信息相融合，通过迭代卡尔曼滤波算法减小估计误差，不断逼近真实轨迹，实现从无人机的导航信息较正。

协同导航的优势在于将少部分具有高精度导航定位能力的无人机的位置信息，广播给其它无人机，使配备低精度导航设备的无人机仍然具有高精度定位能力。

3 无人机编队协同导航模型

在无人机协同导航领域，研究较多的是二维协同导航模型，即将主从无人机投影到二维平面上或者将其调整到同意高度，从而将立体空间问题简化为平面问题，同时减少计算量，但是这样的计算与实际情况会存在较大的误差，且无法知悉无人机在飞行高度上的变化。因此，为使研究结果更具普适性，本文在已有研究的基础上增加了编队在高度方向上的研究。

导航坐标系下，x，y，z 分别为主从无人机在东西方向、南北方向、垂直方向的飞行距离；vx，vy，vz分别为无人机的前向速度、侧向速度、爬升速度；w 为无人机的旋转角速度。

选取导航坐标系下无人机各个方向上的位置，各个方向上的速度作为状态向量。

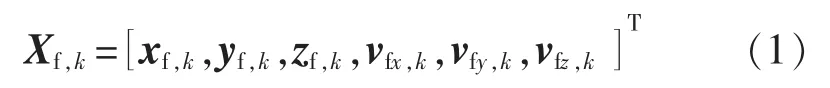
假设，从无人机在x，y，z 方向上做匀速运动，则其飞行过程中的状态方程为

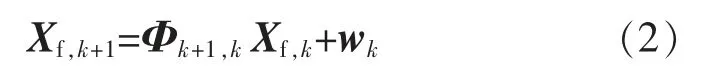
其中

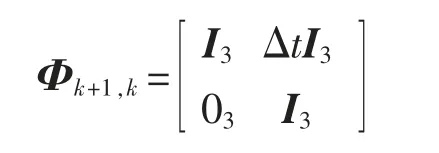
式中：Φk+1，k为系统的状态转移矩阵；Δt 为采样时间；wk为系统噪声矩阵，且属于高斯白噪声。系统的量测方程为

式中：vk为系统量测噪声，且属于高斯白噪声。

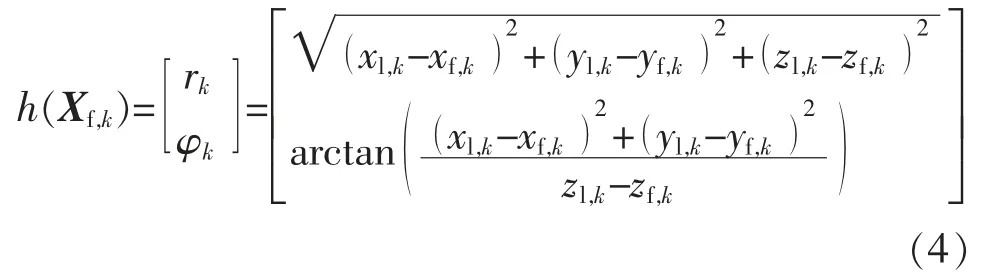
wk，vk满足：

式中：Qk为系统的噪声方差矩阵；Rk为量测噪声方差矩阵。

4 迭代无迹卡尔曼滤波算法

当通过构造与被估计量相同统计特性的sigma采样点进行逼近时，传统的UKF 算法受系统模型噪声影响较大，容易出现精度降低甚至发散的情况[13]。迭代卡尔曼滤波是将观测更新后的状态估计作为新的参考点，对观测方程再次进行算法处理，提高定位精确度同时为保证算法的稳定行，利用Levenberg-Marquardt 方法调整协方差矩阵，保证算法的收敛性[14]。

迭代无迹卡尔曼滤波IUKF 算法步骤如下：

步骤1滤波器初始化。当k=0 时，系统的初始状态值为

系统的初始状态协方差矩阵为

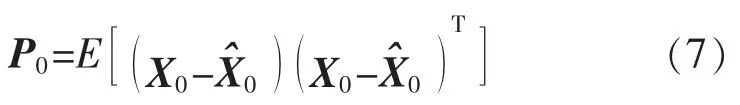
步骤2构造2n+1 个sigma 样本点通过状态方程传递，即

步骤3时间更新。其权重系数为

式中：n 为系统状态的维数；β 为系数，在高斯分布下其最优值为2。

步骤4量测更新。对一步预测值进行UT 变换，产生新的sigma 点集，再次初始化，设定迭代次数为j：

则新的sigma 采样点为

为使算法具有更好的稳定性，采用Levenberg-Marquardt 方法调整预测协方差矩阵，即

变换后状态的一步预测值为

误差协方差矩阵为

从无人机输出的理论方差矩阵为

协方差矩阵为

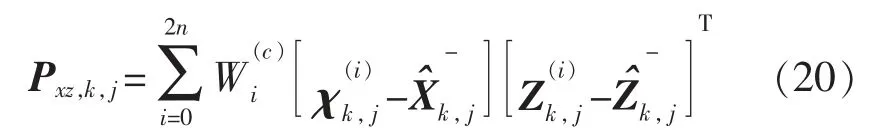
计算卡尔曼增益、更新后的系统状态和更新后的协方差为

步骤5利用Gauss-Newton 方法确定迭代次数。高斯-牛顿方法是用于解决非线性最小二乘问题的一种方法，广泛应用于迭代求解最优化问题中。该方法的主要原理是通过设置代价函数J（X），求解其最小值或者最优值。

在此定义代价函数为

在主从式无人机编队协同导航系统中，由于状态方程为线性方程，而量测方程为非线性方程，此类型求解代价函数最优值转化为求解代价函数的非零极值点。

当J（Xk，j+1）＜J（Xk，j）时，代价函数呈收敛趋势，则第j+1 次迭代结果更接近最优解。

故

步骤6当满足迭代条件时，重复进行量测更新；当不满足迭代条件时，跳出迭代过程，此时可以得到从无人机的位置估计和估计协方差矩阵Pk，j。

5 仿真结果与分析

为直观检测算法的有效性，运用均方误差RMSE（root mean square error）来表示主从式无人机协同导航的精确度。有

为保证单主领航系统的可观测性，假定：主机做固定运动角速度的盘旋上升运动，运动角速度为w=0.1 rad/s；系统在各方向的速度误差为Δv=1 m/s，距离误差为Δ=1 m；从无人机在各方向上以vf=［10 m/s，10 m/s，5 m/s］的速度飞行；主无人机的初始位置为Xl=［315 m，425 m，35 9 m］；从无人机的初始位置为Xf=［349 m，452 m，200 m］。在各种算法下，主从无人机导航系统的导航效果如图1所示。

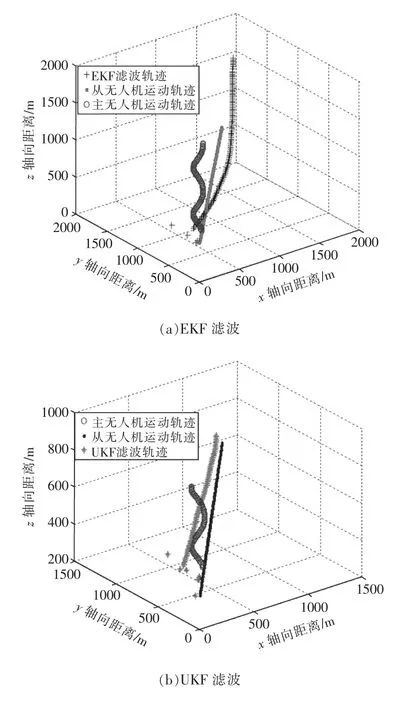
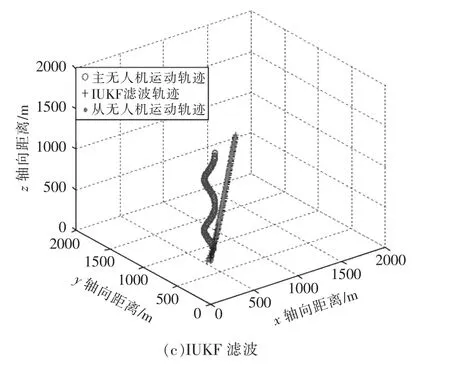
图1 几种滤波算法的估计轨迹示意图Fig.1 Schematic diagram of estimation trajectory of several filtering algorithms

由图可见，主从无人机导航系统在各种算法下的导航效果。主从无人机的飞行轨迹以及滤波后的从无人机飞行轨迹表明，采用Levenberg-Marquardt方法调整预测协方差阵后的IUKF 效果最好，误差最小；UKF 滤波后的轨迹与从无人机实际轨迹逐渐接近；EKF 滤波后的轨迹与从无人机实际轨迹呈发散趋势，精度最差。

由图1中各滤波轨迹示意图，根据主从无人机飞行轨迹以及滤波轨迹的契合程度，可以直观地了解哪种滤波效果更加精确。在此，通过观测各滤波在x，y，z 方向的均方误差，对各滤波进行定量分析。其对比效果如图2所示。

经过直观验证后，从在各个滤波估计下的均方误差对比效果中，比较各滤波处理后的导航精度。

从时间角度来看，各滤波在x 轴均方误差中，IUKF最大误差为20 m，且随着时间的增长，精度逐渐增加，在30 s 逐渐趋于稳定，误差在7 m 左右；UKF 滤波误差首先呈下降趋势，然后迅速增大，在5 s 左右逐渐稳定，最大误差在35 m 左右，在40 s 后误差逐渐下降；EKF 误差起伏幅度较大，最高误差达到120 m左右，而后迅速下降，接着快速上升，呈发散趋势。

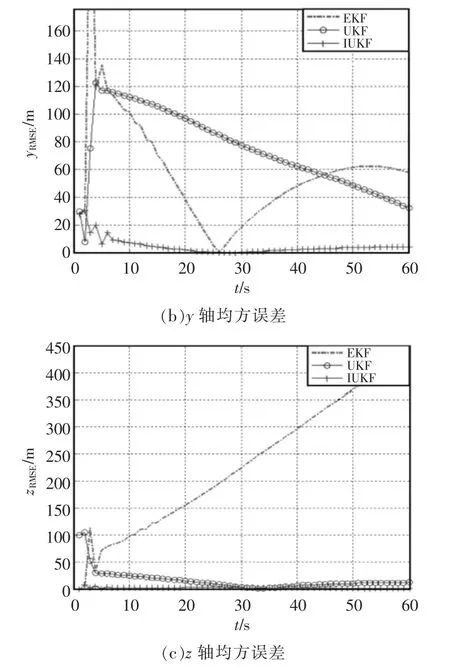
图2 几种滤波在x，y，z 轴均方误差的对比Fig.2 Comparison of root mean square errors of several filters in x，y and z axes

各滤波在y 轴均方误差中，IUKF 误差逐渐下降，在40 s 左右趋于稳定；UKF 最大误差可达到120 m 左右，然后逐渐下降；EKF 误差突变非常明显，在26 s 左右误差精度最好，而后逐渐扩大。

各滤波在z 轴均方误差中，IUKF 误差非常平稳；UKF 最大误差在100 m 左右，而后逐渐下降，在35 s 左右达到最佳值，逐渐趋于稳定；EKF 误差最大值在110 m 左右，在5 s 以后误差呈上升趋势。

综上所述，IUKF 的收敛效果最好，其次为UKF，再次为EKF。从均方误差角度来看，IUKF 的滤波精度最高，其次为UKF，再次为EKF。

根据上述仿真结果可知，采用Levenberg-Marquardt方法，调整预测协方差阵后的IUKF，相较于UKF 及EKF 的导航效果更好。

6 结语

当前对无人机编队协同导航的研究，大都将位置信息投影到二维平面，本文在其基础上增加了飞行高度方向上的研究，使研究结果更具现实意义；在无迹卡尔曼滤波的基础上，为使滤波精度进一步提高，在此提出了迭代无迹卡尔曼滤波算法，并通过高斯牛顿法设置代价函数，确定迭代次数；针对协方差发散问题利用Levenberg-Marquardt 方法调整预测协方差阵，使算法更加平稳，保证算法的全局收敛性；针对非线性滤波在协同导航领域存在收敛速度和收敛精度问题，通过与EKF 和UKF 相对比，证明了本文所提算法的实用性。