电梯门锁啮合长度测试用位移传感器的校正

陈建勋，林晓明，刘 健，邰胜林

（1.广东省特种设备检测研究院珠海检测院，珠海519002；2.珠海市安粤科技有限公司，珠海519000）

截至2018年底，我国电梯保有量已达到627.83万台，我国电梯产量和消费量在全球占比都大于50%，电梯作为一种公共交通工具已得到越来越广泛的应用。随着我国在用电梯数量的不断增多，尤其随着当前信息化和网络化的快速发展，电梯故障和事故得到越来越多的社会和舆论关注，也给电梯制造、安装、维保和检验单位提出了更高的要求。据统计，各类电梯故障和事故中有超过七成与电梯门区系统有关，电梯门区系统的有效检验是确保电梯安全运行的重要保障[1-3]。根据检规《TSG T7001—2009电梯监督检验和定期检验规则——曳引与强制驱动电梯》（下文简称TSG T7001）要求，电梯门锁啮合长度的检验是电梯定期检验过程中的强制检验项目，且每个层站的层门都应该进行该项目的检验[4]。TSG T7001 第6.9 要求“轿厢在锁紧元件啮合不小于7 mm 时才能启动”，检验方法为“目测锁紧元件的啮合情况，认为啮合长度可能不足时测量电气触点刚闭合时锁紧元件的啮合长度”。当目视不足以判断门锁安全触点闭合瞬间啮合长度值是否大于7 mm 时，需对啮合长度值进行测量。

相对于传统的刻度尺法和刻度标注法等常规测试方法外，一种自动化程度较高的测试方法是采用接触式位移传感器配合单片机测试系统进行测试。基于滑动变阻原理的接触式位移传感器由于数据重复性高、结构小巧、成本相对较低等特点在机电类设备检验过程中得到越来越广泛的应用[5-6]，也可应用于电梯门锁啮合长度的测试。为提高测试精度，位移传感器使用前需对其测试准确性进行校准，对不同输出电压下的位移值进行标定，建立位移和电压的函数关系并保存于测试装置软件中。本文用专用位移校准设备进行试验测得多组位移-电压数值，并根据实测数据利用最小二乘方法对不同型式多项式进行拟合，求得拟合方程。通过误差理论对不同拟合结果进行对比分析，找出最适合的校准方程，以提高位移传感器对门锁啮合长度的测试精度。

1 位移传感器工作原理

图1 电梯门锁啮合长度测试原理Fig.1 Test principle of elevator door lock engagement length

门锁啮合长度的原理如图1所示，为方便传感器测量头与门锁活动锁钩接触，在测量头顶部安装一金属片，金属片可伸入活动锁钩正下方。在活动锁钩向下运动与固定锁钩啮合前调节传感器夹具使金属片上表面与固定锁钩上表面平齐。传感器测定电梯关门后电气触点闭合瞬间活动锁钩相对于固定锁钩的下压量（图1所示H），即待检测的啮合长度值，采用传感器测试时一般要求测试精度达到0.2 mm 以上。

啮合长度测试用的接触式位移传感器如图2所示，主要由传感器主体、测量头和复位弹簧组成。测试过程中测量头与待测运动部件接触后，在外部压力下测量头沿图1所示位移方向与传感器主体发生相对运动。传感器基于滑动变阻原理，滑动电阻值与位移大小正相关，对传感器施加已知大小的激励电压可将电阻信号转换成易于采集的电压信号。因此，要获取传感器所测位移值，需提前确定所用传感器输出电压与位移关系。

图2 接触式位移传感器Fig.2 Contact type displacement sensor

2 位移传感器标定试验

采用专用位移校准设备对传感器进行标定，校准设备的位移测试精度可达0.02 mm，标定试验装置如图3所示。位移传感器安装于磁吸座的万向支架上，观察气泡水准仪，同时调节万向支架使传感器受压方向处于铅垂方向。容栅传感器可与压头同步运动，转动校准设备的滚轮使压头下移至刚好接触到安装于传感器测量头上的金属片上表面，此时将容栅传感器位移值置零。用精密电源提供传感器激励电压，电压标称值为3.29 V，传感器输出电压由示波器记录，所测位移值由容栅传感器记录。

实测某位移传感器得到不同输出电压下的位移数据如图4所示。受传感器自身结构影响，位移为2 mm 以内为测试盲区，在该位移区间内传感器输出电压近似为零，不随位移变化而规律性变化。由于2 mm 左右的啮合长度在实际电梯检验过程中通过目视即可识别，故标定时无需考虑2 mm 以内位移数据，仅使用位移大于2 mm 的数据进行传感器校正，总共38 组“位移-电压”数据。

图3 位移传感器标定试验装置Fig.3 Calibration test device for displacement sensor

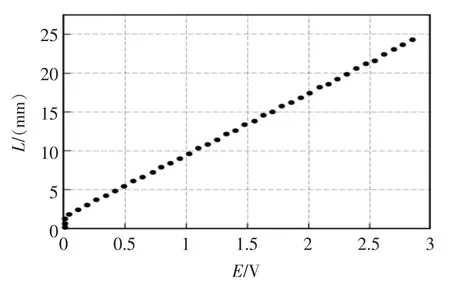
图4 位移与电压关系散点图Fig.4 Scatter plot of displacement and voltage relationship

3 数据拟合方法

3.1 最小二乘法多项式拟合原理

拟合公式的选择对拟合误差大小、算法复杂性有很大程度影响。一般来说拟合公式形式结构越复杂越能反映数据的真实变化趋势，但过于复杂的拟合公式将使拟合算法变得过于复杂，求解效率低下，甚至通过计算机也较难计算出拟合系数[7]，实际工程应用中多选择以次数为主体的多项式拟合公式。

最小二乘法是一种数学优化技术，又称最小平方法，它通过最小化误差的平方和寻找数据的最佳函数匹配，随着计算机计算能力的不断提高，最小二乘法拟合在工程领域得到越来越广泛的应用。利用最小二乘法可求得多项式形式的拟合方程，使得利用该方程求得的因变量数值与实际数据之间误差的平方和最小[8-10]。假设有n 组数据序列（x1，y1）、（x2，y2）、…、（xn，yn），其自变量向量为

对应的因变量向量为

若待求解的拟合函数为k 阶多项式形式

X 中各元素代入f（x）求解得到的函数值f（xi）与Y 中对应元素yi之间偏差的平方和为

拟合的目的在于确定多项式系数向量使得S达到最小值，式（3）对应的系数向量为

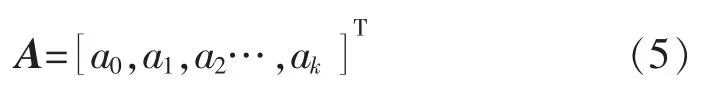
S 分别对系数a0、a1、a2…ak求偏导，使其结果为0，整理可得：

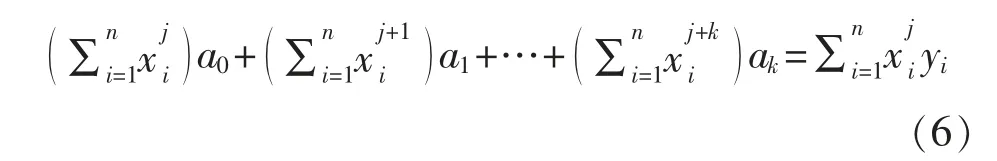
式中：j 为系数序号，取值范围为0～k。

将式（6）表示成矩阵形式：

其中：

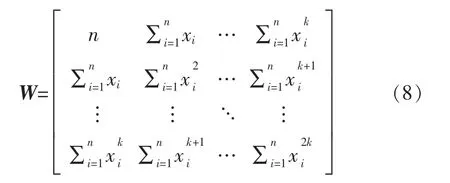
且有：

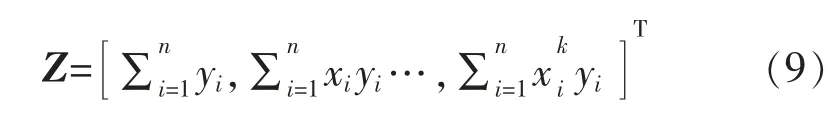
求解矩阵方程（7）即可得到多项式系数向量A：

3.2 拟合过程的实现

用Matlab 软件实现数据拟合与拟合结果分析。用polyfit 函数实现多项式拟合，其格式为

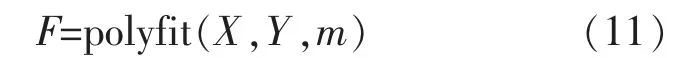
式中：m 为待拟合多项式的最高次数。该函数以最小二乘意义求解出符合拟合数据f（x（i））至实测数据y（i）的n 次多项式f（x）的系数向量F。

调用polyval 函数可实现各个自变量拟合函数值的求解，其格式为

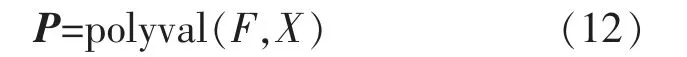
式中：P 为自变量向量X 带入拟合方程f （x）求解得到的因变量向量。

4 拟合结果与分析

4.1 拟合结果

去除位移2 mm 以内测试死区数据后，对试验数据分别进行线性拟合、抛物线拟合和三次多项式拟合，最小二乘拟合曲线结果如图5所示，拟合函数形式及计算的多项式系数如表1所示。可知3 种函数形式的拟合结果都接近于实测数据，当位移值大于15 mm 时，抛物线拟合和三次多项式拟合结果与实测数据更为接近，而线性拟合结果计算的位移值比实测数据略小。

图5 最小二乘拟合曲线Fig.5 Least squares fit curve

表1 多项式拟合结果Tab.1 Polynomial fitting result

4.2 误差分析

误差是不可避免的，在校准试验得到的用于拟合的测试数据也会受校准装置自身位移和电压测试误差的影响，故用于分析的原始数据本身存在一定的测量误差，此外使用计算机拟合过程中也会产生一定的计算误差。本文选用残差、算数平均误差和标准误差3 个评估指标对拟合结果进行误差分析[11]。

4.2.1 残差

拟合位移值实测实测位移值的残差为

式中：vi为残差，Li为传感器实测位移值，f（Ei）为拟合方程计算得到的位移值，各个数据点对应的残差总体越小说明方程拟合效果越好。

不同拟合方式得到的各数据点残差结果如图6所示。抛物线拟合和三次函数拟合的残差在零点附加波动，在±0.2 mm 以内，说明这2 种拟合结果比较接近，拟合精度较高。随着传感器所测位移变大，其输出电压变大，此时线性拟合的残差越来越大，甚至达到0.8 mm，存在较大拟合误差。

图6 拟合结果残差图Fig.6 Residual plot of fitting result

4.2.2 算数平均误差

算数平均误差为残差绝对值的平均值：

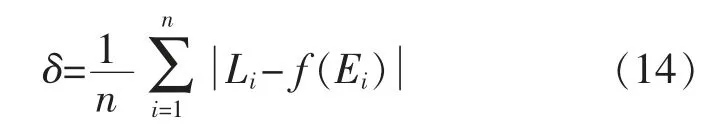
式中：δ 为拟合的算术平均误差；n 为数据点个数。δ越小则拟合精度越高。三种拟合方式算数平均误差计算结果如表2所示，线性拟合算数平均误差最大，抛物线拟合和三次函数拟合的算数平均误差均小于0.1 mm，且两者结果较为接近。

4.2.3 标准误差

标准误差能够很好地反映出数据拟合的精密度，其对对一组测量中的特大或特小误差反映非常敏感，计算公式为

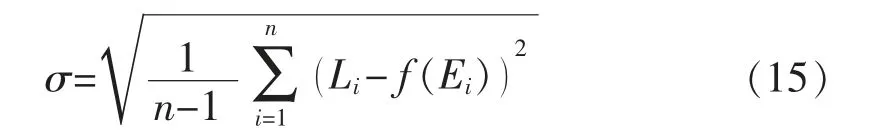
式中：σ 为标准误差。σ 越小，拟合方程精度越高。三种拟合方式标准误差计算结果如表2所示，三次函数拟合的标准误差最小，精度最高。

4.3 校准结果评价

三种拟合方式中，线性拟合误差最大，尤其在较大位移处已明显偏离实测数据，三次函数拟合的残差、算数平均误差和标准误差都最小，精度最高，为最优拟合。因此，选取三次函数拟合结果作为该位移传感器的校准方程：

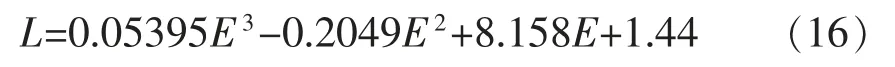
5 结语

本文选用线性函数、抛物线函数和三次多项式函数三种方程形式，用最小二乘多项式拟合方法对电梯门锁啮合长度测试用位移传感器的位移-电压特性曲线进行了曲线拟合，通过Matlab 计算出位移和电压函数关系式，并计算出拟合误差。三次多项式函数拟合的算数平均误差和标准误差最小，残差控制在±0.2 mm 以内，提高了电梯门锁啮合长度测量的准确性，满足测试精度的要求。