基于双树复小波分解的云量时间序列模型预测

白云博 欧阳斯达 杨朦朦 夏学齐 王婷

基于双树复小波分解的云量时间序列模型预测

白云博1,2欧阳斯达2杨朦朦3夏学齐1王婷4

（1 中国地质大学（北京），北京 100083）（2 国土卫星遥感应用中心，北京 100048）（3 山东科技大学，青岛 266590）（4 成都理工大学，成都 610059）

针对传统云量预测模型应用于高分辨率卫星影像云量时间序列数据时存在的实用性差、拟合效果差及预测结果准确度低的问题，提出了一种基于双树复小波分解的云量时间序列组合模型预测方法。该方法利用DT-CWT分解的方法提取出云量时间序列的低频趋势信息和高频随机信息，对低频和高频序列分别应用时间序列分析与Elman神经网络的预测方法，然后将两个序列的预测结果重构得到最终的云量预测结果。实验结果表明，应用双树复小波分解的低频信息可以更好的反应云量变化趋势，高频信息也可以更好的保留云量变化的随机信息。该方法预测结果的平均绝对误差和均方根误差相比传统预测模型均有所减小，预测准确度有所提高，能够更好的拟合高分辨率卫星云量时间序列的变化规律。在卫星成像任务规划时将云量预测的结果作为参考信息，选择云量覆盖较小的时间窗口，可以获取更高品质的卫星有效成像数据。

高分辨率影像 双树复小波分解 时间序列分析 神经网络 卫星遥感云量预测 遥感载荷

0 引言

随着遥感技术的发展，越来越多的应用领域，如全球矿产资源、作物估产、水资源、森林生态和城市变化检测等，需要高分辨率、高品质卫星影像数据为生产、生活提供信息支持[1]。在卫星运行中，针对预期的成像条件进行成像预估，可为任务计划提供重要依据[2]。其中，对于高分辨率光学卫星影像的获取，云量占比是影响卫星成像品质的重要因素，也是判别影像是否为有效数据的主要因素[3]。对于特定的成像目标区域，为提升少云或无云的高品质卫星影像数据的获取成功率，需要提前预判成像区域的云量覆盖情况，选择在云量较少的时段进行高效率的卫星成像。因此，对卫星成像云量进行预测，提高预测的准确度，对最大程度发挥光学卫星影像获取能力以及提高卫星拍摄效率都有着重大的意义。

在云量预测相关模型方法方面，应用较广泛的就是与气象相关的短期预测模型，此方法主要是利用一些模型方法，如模式识别、交叉方法等对云量变化进行短期预测，预测期通常为几小时[4]。文献[5]等将卫星图像（第二代气象卫星）与空中摄像机（鱼眼镜头相机）的图像结合使用来进行云量预测，短期（1h）或中期（3h）预测成功率较高。而一般卫星的成像任务计划通常提前一至两天，短期预测模型外推的几小时预测结果较难为任务计划提供可靠预测信息[6]。此外，采用时间序列分析预测是目前较为常用的中长期云量预测方法，文献[7]等通过分析云量时间序列的特点对其进行分类，然后采用不同模型对未来云量进行预测，应用在气象卫星“风云”系列等卫星数据上，得到了较好的预测效果。文献[8]等也应用时间序列分析的方法，在低分辨率的国际卫星云气候学计划月平均云量数据上，得到了很好的验证。但对于类似“资源三号”（ZY-3）、“高分一号”（GF-1）等高分辨率卫星影像所包含的云量数据，因空间分辨率的提高及时间分辨率的降低，导致云量变化规律被随机性干扰或掩盖，干扰了时间序列预测模型对数据本质规律的识别。

为解决以上问题，降低高分辨率影像云量数据的随机性干扰，本文提出一种基于双树复小波分解的云量时间序列分析的高分辨率卫星成像预测方法，通过对高分辨率卫星成像的云量时间序列数据进行双数复小波分解，提取出云量时间序列的低频趋势信息和高频随机信息；对低频、高频信号分别选取时间序列分析、人工神经网络进行预测，再将预测结果重构为最终的成像云量预测值。本文采用ZY-3、GF-1等卫星2013—2019年的云量数据作为数据源，并以月为时间分辨率尺度单位，通过选取攀枝花、喀什、包头等地区约为20km×20km矩形区域作为实验研究区进行实验，与针对于低分辨率气象卫星数据的传统预测方法相比，该方法可以有效挖掘历史高分辨率影像长序列云量数据的内在联系，提取云量数据的趋势信息，在规避了随机信息对变化规律的影响的同时，也有效利用了易被忽略的高分辨率影像时间序列的随机信息的潜在规律。

1 研究内容

1.1 双树复小波

传统离散小波变换分解后存在频率混叠及平移敏感性等问题，Kingsbury等人提出了双树复小波变换（dual-tree complex wavelet transform，DT-CWT）[9]。2005年，Selesnick等在原有双树复小波基础上设计出的新的双树复小波变换分解与重构的算法，推动了双树复小波变换的发展[10]。

采用Selesnick等提出的DT-CWT方法，将高分辨率存档云量数据进行分解，得到低频信息和高频信息。假设造成成像结果的各类不确定性条件一致，所有的因素的随机性和趋势性，都体现在了成像结果的高频和低频信息上，低频信息可以较好的保留原始云量趋势走向信息，高频可以很好的保留因其他因素所导致的云量突变信息。DT-CWT构造过程如图1所示。

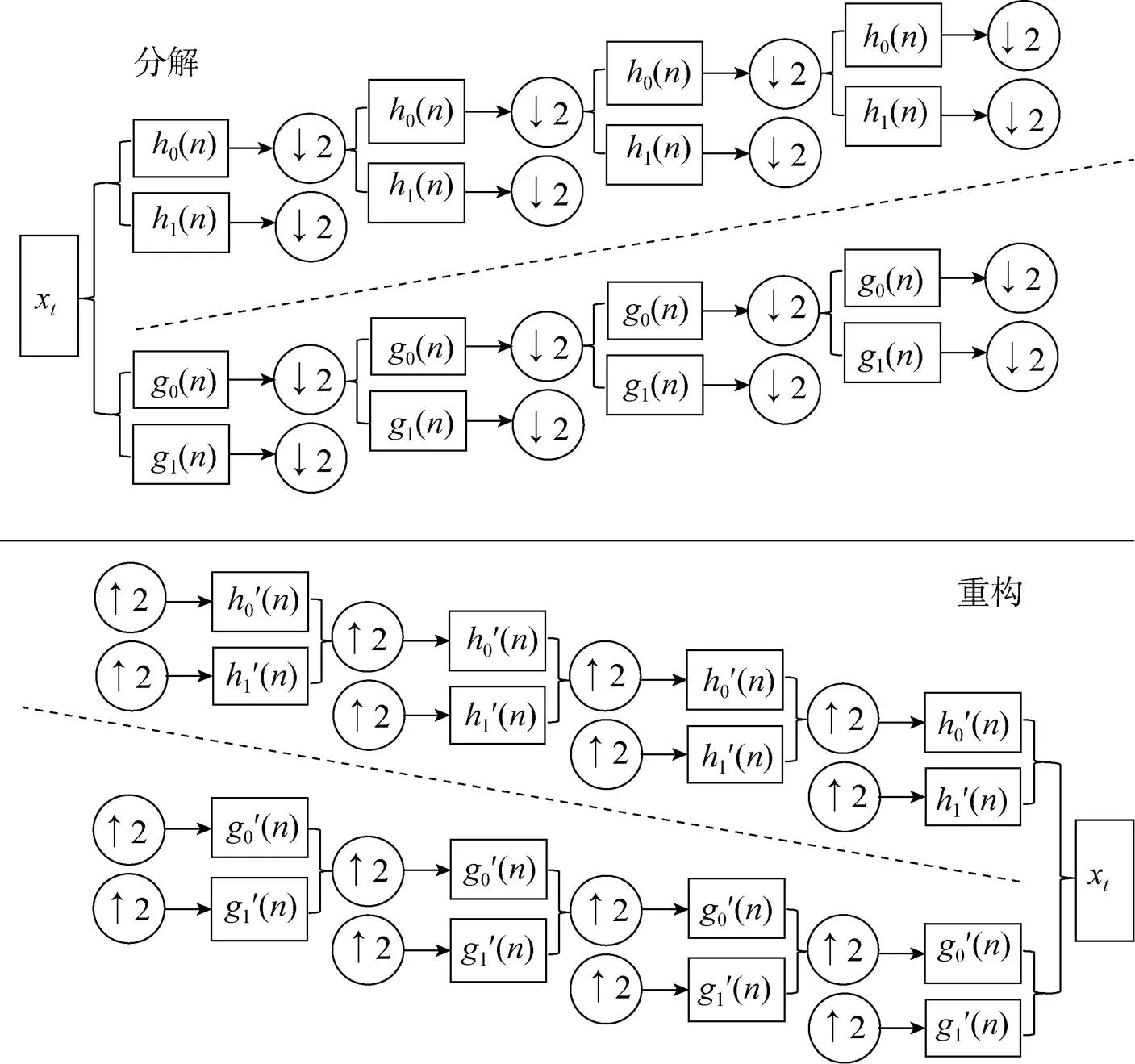
图1 DT-CWT的分解与重构

不同于传统的离散小波变换，这里是将复小波的实部和虚部分离开，采用二叉树结构的两路离散小波变换形式，两棵并行的实小波变换树来对信息进行分解与重构，其中一棵为实部树，另一棵为虚部树[11]。在分解与重构过程中，始终保持虚部树的采样位置点正好位于实部树的中间，这样就能使得两树分解系数达到信息互补[12]，这样利用实数的小波变换来实现带有复数形式的复数小波变换，根据DT-CWT的构造方法[13]，复小波表示为

1.2 时间序列分析

时间序列分析广泛应用于气象水文[14]，通过时间序列分析的方法挖掘出低频序列数据内在的联系[15]，找到云量序列变化的规律，建立能够准确描述这种变化关系的时间序列模型，然后进行数据序列趋势的预测，可宏观的描述云量时间序列趋势走向。

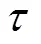
非平稳序列通过判定是否具有周期性，分为普通非平稳序列和季节性非平稳序列[17]。主要判断标准是自相关函数ACF（auto-correlation function）。对于一个第期云量时间序列的自相关函数为

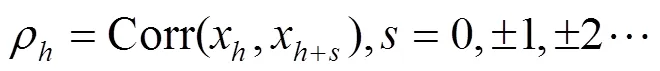
式中为第期的偏移量，随机过程Corr为

式中 Cov表示求云量序列的协方差；Var表示求云量序列的方差。云量作为一种天气自然现象，决定了其季节周期为12，即如果ACF具有周期性特点，并且在滞后期12的整数倍出现峰值，则存在季节特征。若不具备周期性特点，在滞后期12的整数倍不出现峰值，则序列不存在季节特征[18]。

对于非平稳序列，通常采用一阶差分方程转换成平稳时间序列。差分方程为

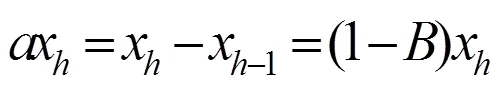
式中为差分算子；为延迟算子。如果高分辨率卫星影像云量序列存在周期性特点，则在滞后期12的整数倍出现峰值，采用季节性差分自回归滑动平均模型（seasonal autoregressive integrated moving average，SARIMA）进行预测，否则为普通非平稳序列，采用差分整合移动平均自回归模型（autoregressive integrated moving average model，ARIMA）进行预测。

1.3 人工神经网络

由DT-CWT分解高分辨率云量数据得出的高频序列包含了大量的随机信息，表现出规律性差、振幅跨度大、波动频率不规则等特点，且对于以月为观测数据的时间尺度而言，高频信息中所包含的随机性是云量变化规律中不可忽略的影响因素。所以本文采用Elman神经网络作为预测模型，既可以有效应对高频随机信息规律性差的问题，又较好的解决高频信息难以适应单一变化类型预测模型的问题。

Elman神经网络是典型的循环神经网络（recurrent neural network，RNN），具有良好的逼近能力和适应时变特性，用于预测混合预测模型中由小波分解的高频信息[19]。由于其具有较强的学习能力、联想力和容错力，Elman神经网络被广泛用于时域和空域的模式识别[20]。Elman神经网络由输入层、隐含层、承接层和输出层组成，其结构如图2。

图2 Elman神经网络

Elman神经网络与前馈型网络相比，多了一个承接层，用来记忆隐含层单元的输出值并返回给输入，构成局部反馈，其传输函数为线性函数，但多了一个延迟单元，可回忆过去的状态，使网络具有动态记忆功能[21]。Elman神经网络的数学公式为：

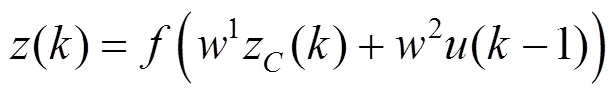
利用高频随机序列构造训练样本，确定神经网络的结构对网路进行训练，使误差沿梯度方向下降，当达到设定的阈值标准的时候，确定模型的权值，利用训练好的网络模型对高频随机序列进行预测。

2 实验方法设计

2.1 方法流程

本文设计的方法流程主要分为几个步骤，如图3所示。

图3 方法流程图

1）采用ZY-3、GF-1等高分辨率卫星影像历史云量存档数据，并以月为时间分辨率对研究区高分辨率影像云量数据进行提取，以百分比的形式进行记录，作为原始数据源。

2）由于国产高分辨率卫星影像时间分辨率有限，存在个别月份数据缺失，为保证实验数据的连续性但又不偏离实验数据的准确性，本研究采用线性拟合的方法对原始数据进行缺失数据的拟合，补充缺失数据得到待分析数据源。

3）对研究区数据源全部进行DT-CWT分解，分别得到低频趋势序列信息和高频随机序列信息，将两序列信息分别分为前段样本训练组和后段预测对比组。

4）对高、低频序列信息样本训练组的数据采用不同的方法进行分析、建模、预测，低频趋势序列信息选择时间序列分析法，采用ADF检验判定时间序列模型并进行预测，高频随机序列信息选用Elman神经网络进行训练，通过训练后神经网络进行预测。

5）将低频趋势序列信息和高频随机序列信息的预测结果进行重构，得到最终的云量预测结果。

6）分别将全部序列的低频信息与原始云量、预测组的低频信息预测值与实际值、高频信息预测值与实际值、重构云量预测值与原始云量实际值进行对比，以平均绝对误差和均方根误差作为评价指标进行评价分析。

2.2 数据预处理

本研究选取攀枝花、喀什、包头三个研究地区进行实验，三个地区的地理位置、气候特征等差异较大，云量覆盖情况也有显著不同。攀枝花地区云雨天气较多，阳光照射时间少，地区云覆盖情况比较明显，云量大部分时间处于50%以上。而喀什和包头地区云雨天气相对较少，光照比较充足，特别是包头地区云量大部分时间处于40%以下，同时两地极端天气时云量差异大，特别是喀什云量变化频率高。

以月为单位下载研究区面积为20km×20km的高分辨率卫星影像，时间跨度从2013年5月—2019年 2月，共60~70个月，分为每月一期。对下载的高分辨率影像进行云量占比判断，得到以百分数形式记录的云量序列。

对于实验中存在卫星影像缺失问题，导致云量数据的不连续，本研究采用线性拟合的方法将研究区云量数据拟合出线性方程，根据拟合方程计算出缺失云量数据，确保实验数据的时间连续性，以得到可进行时间序列分析的数据源。对数据源全部数据进行分组，分为前段约50~60期的样本训练组和后段约10期的预测对比组。并对全部序列进行DT-CWT分解。

2.3 低频趋势信息预测

应用EVIEWS软件对样本训练组分解的低频信息进行平稳性检验，依据单位根统计量ADF与非平稳假设的显著性水平1%～10%的临界值进行比较，判断序列类型。当ADF全部小于临界值，则不接受序列有单位根（非平稳）的假设，该序列为平稳序列，否则为非平稳序列。

本研究三个研究区经过ADF检验，均为平稳序列，根据自相关函数图分析计算出ARMA模型参数。以样本训练组的所有数据为基础，利用具体的ARMA模型进行低频序列的预测。逐次向后预测单个序列数值，经多次预测推进后，得到预测组全部预测值。将预测结果与实际低频趋势信息进行对比，计算两组数据之间的平均绝对误差和均方根误差，进行评价分析。

2.4 高频随机信息预测

针对于样本训练组分解出的高频信息，首先对高频序列数据进行归一化处理，输入全部样本训练组序列对Elman神经网络进行训练，使训练后神经网络具备此研究区高频信息随机变化的特性。用训练好的Elman神经网络，对高频信息预测组进行预测，并进行反归一化处理，得到高频预测结果。将高频预测结果与实际高频信息进行对比，计算两组数据之间的平均绝对误差和均方根误差，进行评价分析。

2.5 数据重构

对包含训练组实际值和预测组预测值的全部序列预测的低频趋势信息和高频随机信息进行DT-CWT重构，并进行[0，100]有限区间截断处理，得到最终云量的预测结果，将云量预测结果与原始实际云量信息进行对比，并求出两组序列的平均绝对误差MAD和均方根误差RMSE，进行评价分析。

3 实验过程及结果分析

3.1 攀枝花研究区

选取攀枝花研究区2014年10月—2019年1月的历史云量数据，其中缺失2017年6月和2018年6月数据，应用线性拟合将数据补全为52期，分成前40期作为样本训练组，后12期作为预测对比组。实验结果如图4所示，表1为攀枝花研究区评价指标。

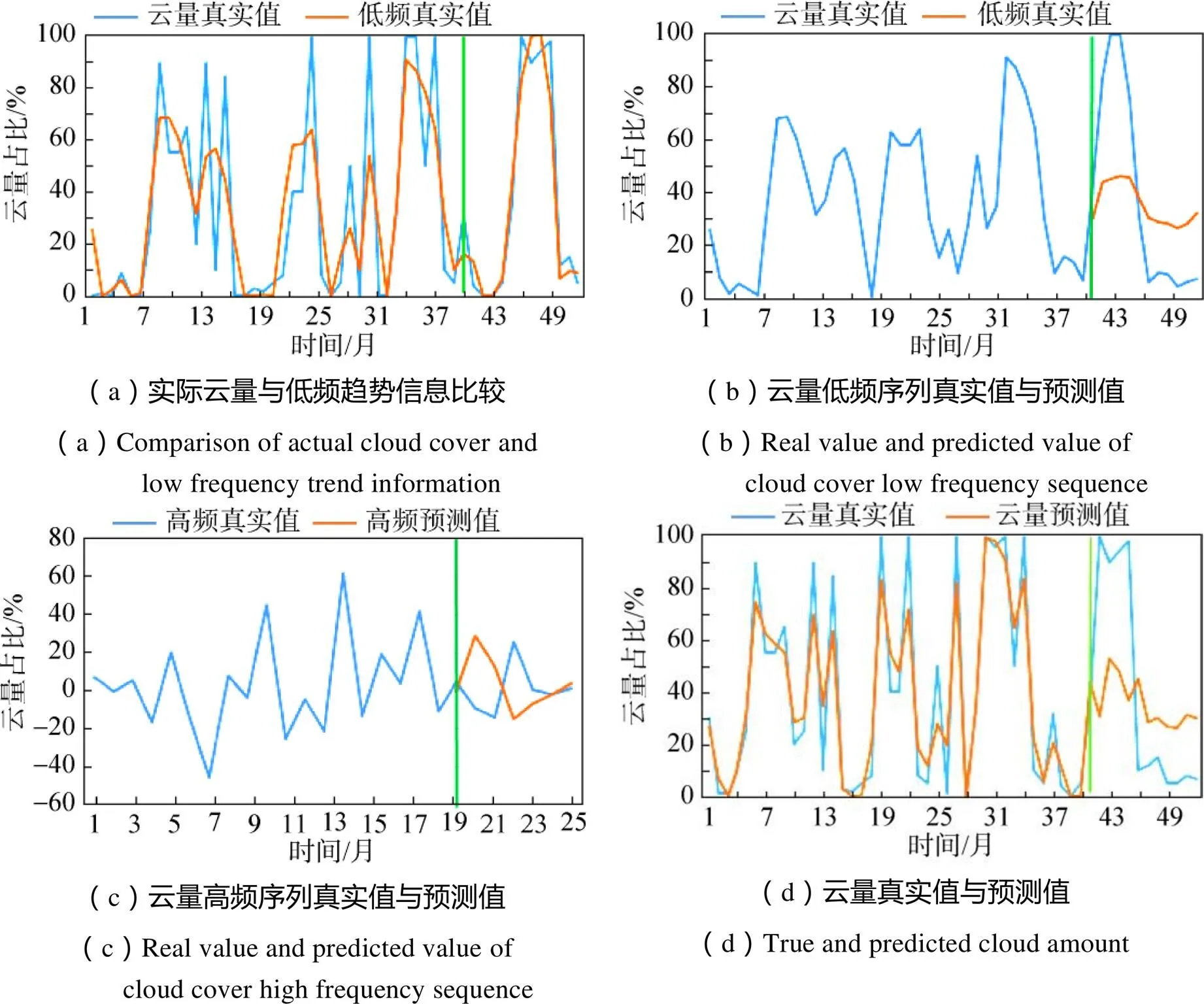
图4 攀枝花研究区实验结果

表1 攀枝花评价指标

Tab.1 Panzhihua Evaluation Indicators

对全部52期数据应用DT-CWT分解，得到低频趋势信息和高频随机信息。图4（a）中，横坐标表示时间，纵坐标表示云量所占百分比，蓝线代表实际云量，红线代表提取的低频趋势信息。由图4（a）可知，DT-CWT实现了低频趋势序列信息的分离，获取的低频趋势序列较好的反映出了云量真实序列的变化趋势，基本没有相位差。表1中实际云量与低频趋势信息的MAD为14.754 56，RMSE为19.294 746 35。因此，选用此低频趋势序列信息作为训练样本，对未来云量变化的趋势进行预测。

对于低频趋势信息进行ADF检验，单位根统计量ADF=–4.236 557，小于EVIEWS软件给出的显著性水平1%～10%的临界值，所以不接受序列有单位根（非平稳）的假设。该低频趋势序列为平稳序列，选用ARMA模型进行预测，预测结果如图4（b），图中蓝线代表云量低频趋势信息，红线代表低频预测信息，由图4（b）可知，预测值可以基本反应低频信息的趋势变化，波动情况基本一致，不存在相位差，由表1可知，MAD为26.654 42，RMSE为29.542 39。整体评价分析，低频趋势序列的预测结果较理想。

对于高频随机信息，采用Elman神经网络进行预测，将分解所得26期高频随机序列分为两组，前20期数据作为数据源组，构造训练样本对神经网络进行训练，后6期数据作为预测样本。图4（c）中，蓝线代表高频序列真实值，红线代表预测值，由图4（c）看出，Elman神经网络的预测结果反映了云量高频信息的变化趋势，预测值的波动情况与实际高频随机序列波动情况基本一致。由表1可知，MAD为18.532 557 36，RMSE为25.349 25，可见Elman神经网络的高频随机序列预测结果较为理想。

最后，包含预测值的低频趋势信息和高频随机信息进行DT-CWT重构，得到包含后12期云量预测值的最终云量结果，如图4（d）。图中，蓝线代表云量信息的真实值，红线代表预测值。由图4（d）可以看出云量预测值与真实值比较贴合。由表1可知，本文方法的MAD为14.881 681 25，RMSE为20.472 31，相比较传统的云量预测方法MAD为16.369 568 14，RMSE为23.685 23，本文方法的预测准确度有较大的提升。重构后的预测值更为精确的反映了云量真实值的变化趋势。

3.2 喀什研究区

选取喀什研究区2013年7月—2019年2月的历史云量数据，其中缺失16年2月和18年4月数据，应用线性拟合将数据补全为68期，分为前58期数据源组，后10期作为预测对比组。实验结果如图5，表2为喀什研究区评价指标。

图5 喀什研究区实验结果

表2 喀什评价指标

Tab.2 Kashi Evaluation Indicators

低频趋势信息与实际云量MAD为15.989 41，RMSE为21.721 02，基本反映了云量的变化趋势。通过时间序列分析方法建模预测出的低频趋势序列的变化趋势基本符合。Elman神经网络预测出的高频信息趋势符合，波动基本一致。图5（d）中，重构后的云量预测序列走势与云量真实值相似，仅部分时间节点上的云量预测值与实际值不同，但节点两端的变化趋势基本一致。同时由表2可知，本文方法的云量真实值与预测值的MAD为13.842 93，RMSE为19.366 12，传统方法的MAD为14.658 13，RMSE为21.335 41。由数据结果可知，本文方法具有明显的优势，基本反映了云量近期的变化趋势。

3.3 包头研究区

选取包头研究区2013年6月—2019年1月的历史云量数据，其中缺失13年10月和18年5月数据，应用线性拟合将数据补全为68期，分为前58期数据作为数据源组，后10期数据作为预测对比组。实验结果如图6，表3为包头研究区评价指标。

图6 包头研究区实验结果

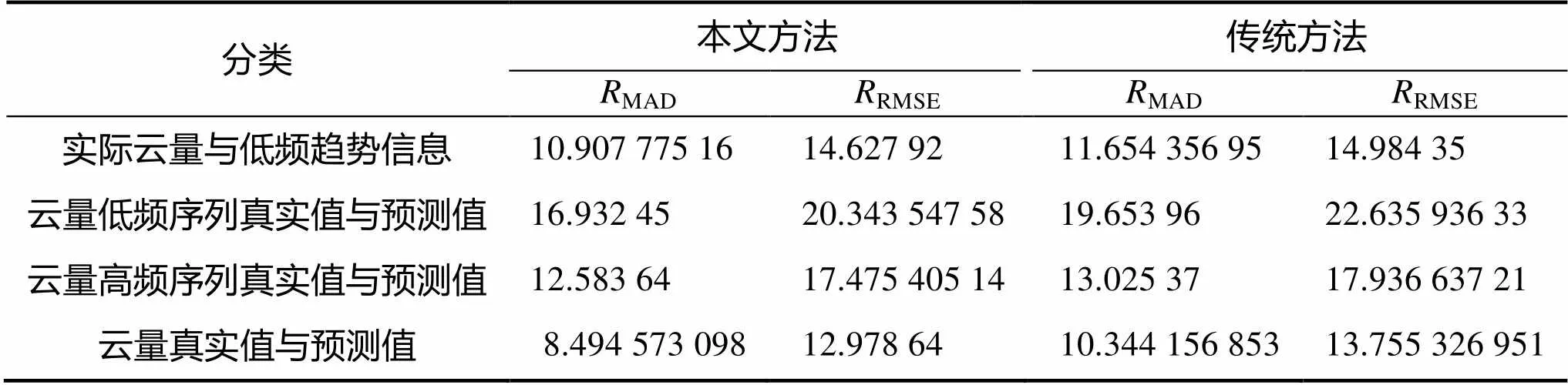
表3 包头评价指标

分解后的低频趋势信息与实际云量的MAD为10.907 775 16，RMSE为14.627 92，可以很好的反应云量信息的变化趋势。低频信息的预测值与真实值的MAD为16.932 45，RMSE为20.343 547 58，变化趋势较为吻合，预测值与真实值误差较小。经过Elman神经网络预测的高频信息反映了云量高频信息的变化趋势，相位无偏差。本文方法的云量真实值与重构后的预测值MAD为8.494 573 098，RMSE为12.978 64，传统方法的MAD为10.344 156 853，RMSE为13.755 326 951，误差值明显减小，且由图6（d）可以看出包头地区应用本文方法重构后的云量预测值变化趋势与实际值也较符合，仅有一处时间节点预测值与真实值误差较大，其他时间节点处的预测走向反映了云量真实值的波动情况，时间适用性较好。

3.4 研究区预测特点分析

本研究选取攀枝花、喀什、包头三个地区进行实验，因为三个地区的地理位置、气候特征等差异较大，因此云量覆盖情况也有显著不同。攀枝花地区云雨天气较多，阳光照射时间少，地区云量覆盖情况会比较明显，44.2%的数据达到30%以上云量覆盖。喀什地区云雨天气相对较少32.3%的数据达到30%以上云量覆盖，光照比较充足，具有云量变化差异大的特点。包头地区气候干燥云覆盖较少，11.8%的数据处于30%以上云覆盖量，光照比较充足，也存在极端变化天气。

3.5 预测结果共性评价

通过对三个研究区高分辨率卫星影像云量数据进行双树复小波分解，得到了低频趋势信息和高频随机信息，低频趋势信息可以较好的反应原始云量数据的趋势走向信息，高频信息也反映了云量信息随机性强的特点。

对三个地区的云量低频序列采用时间序列方法预测，预测结果表明：对双树复小波分解后低频信息进行时间序列分析，对高分辨率卫星影像云量趋势预测有较好的适用性，预测结果与云量真实值变化趋势基本都相符。

对三个地区的云量高频序列采用神经网络方法预测，预测结果表明：对双树复小波分解后高频信息进行Elman神经网络训练，能有效提取高分辨率卫星影像云量的随机性特征，预测值的波动情况与实际的高频随机序列波动情况基本一致。

将云量低频序列预测值与高频序列预测值通过DT-CWT重构后得到云量数据预测值，与云量真实值拟合效果较好，预测值能较好的刻画云量数据在各时间节点的走势，对三个研究区的评价指标平均绝对误差和均方根误差进行分析表明，与传统预测方法相比较，本文的预测准确度大大提升，将高频与低频信息重构可有效减小误差，云量预测值兼顾了研究区实际的云量变化趋势性与随机特征，准确预测云量变化趋势的同时刻画了变化细节。

4 结束语

本文所提出的结合复小波分解的时间序列分析云量预测方法，可以解决传统云量预测方法对高分辨率遥感影像数据适用性差、拟合效果差、时间适应性差及预测结果精度低的问题。该方法运用了复小波分解数据分离思想，充分挖掘了隐藏在云量数据内的深层规律，采用DT-CWT分解将历史云量数据分离出低频趋势序列和高频随机序列，对不同的序列采用不同的方法进行分析建模预测，最后再重构出最终的预测结果。该方法有效地吸纳了国产高分辨率卫星长期存档影像数据源的优势，充分利用了存档影像云量数据中的趋势与随机信息，在准确预测云量变化趋势的同时增加了细节处的刻画，改善了云量预测的符合度，提高了云量预测的精度，为高分辨率光学卫星的成像任务规划提供了很好的技术支持，有效地减少规划任务不当而造成的卫星资源的浪费。

云量本身的影响因素众多，变化较复杂，要高精度预测云量变化的趋势，得到云量的准确值，对存档影像的时间频率有较高要求。随着卫星对地观测技术的不断发展，高分辨率遥感影像数据的空间分辨率不断增加，存档影像的时间分辨率越来越大，云量预测的精度将会更加准确。本文对基于双树复小波分解的云量时间序列分析的高分辨率卫星成像预测方法进行了可行性的验证，但尚未实现全自动化的数据分析，大范围区域（全国范围）的实验还有待进一步验证。

[1] 贺仁杰, 高鹏, 白保存, 等. 成像卫星任务规划模型、算法及其应用[J]. 系统工程理论与实践, 2011, 31(3): 411-422. HE Renjie, GAO Peng, BAI Baocun, et al. Imaging Satellite Mission Planning Model, Algorithm and Its Application[J]. System Engineering Theory and Practice, 2011, 31(3): 411-422. (in Chinese)

[2] 陈世平. 景物和成像条件对遥感图像品质的影响[J]. 航天返回与遥感, 2010, 31(1): 1-10. CHEN Shiping. Effects of Scenery and Imaging Conditions on Remote Sensing Image Quality[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(1): 1-10. (in Chinese)

[3] 余婧, 陈浩, 李军. 地理因子对卫星成像质量影响预估方法研究[J]. 遥感信息, 2011(5): 104-108. YU Jing, CHEN Hao, LI Jun. Study on the Method of Predicting the Influence of Geographical Factors on Satellite Imaging Quality[J]. Remote Sensing Information, 2011(5): 104-108. (in Chinese)

[4] 刘瑞霞, 刘玉洁, 杜秉玉. 中国云气候特征的分析[J]. 应用气象学报, 2004, 15(4): 468-476. LIU Ruixia, LIU Yujie, DU Bingyu. Analysis of Cloud Climate Characteristics in China[J]. Journal of Applied Meteorological Science, 2004, 15(4): 468-476. (in Chinese)

[5] ALONSO J, TERNERO A, BATLLES F J, et al. Prediction of Cloudiness in Short Time Periods Using Techniques of Remote Sensing and Image Processing[J]. Energy Procedia, 2014, 49: 2280-2289.

[6] 欧阳斯达, 汪汇兵, 何召宁, 等. 基于大数据回归分析的卫星有效成像概率预估[J]. 航天返回与遥感, 2017, 38(3): 116-124. OUYANG Sida, WANG Huibing, HE Zhaoning, et al. Estimation of Satellite Effective Imaging Probability Based on Big Data Regression Analysis[J]. Spacecraft Recovery & Remote Sensing, 2017, 38(3): 116-124. (in Chinese)

[7] 王喆文, 黄鹏, 林友明. 利用小波分解的时间序列云量预测方法[J]. 遥感信息, 2016, 31(4): 1-8. WANG Zhewen, HUANG Peng, LIN Youming. Time Series Cloud Prediction Method Using Wavelet Decomposition[J]. Remote Sensing Information, 2016, 31(4): 1-8. (in Chinese)

[8] 王志信, 林友明, 黄鹏, 等. 基于时间序列的中亚地区云量特征分类及云量变化趋势[J]. 遥感技术与应用, 2014, 29(5): 839-845. WANG Zhixin, LIN Youming, HUANG Peng, et al. Classification of Cloud Amount Characteristics and Variation Trend of Cloud Amount in Central Asia Based on Time Series[J]. Remote Sensing Technology and Application, 2014, 29(5): 839-845. (in Chinese)

[9] KINGSBURY N. Complex Wavelets for Shift Invariant Analysis and Filtering of Signals[J]. Applied and Computational Harmonic Analysis, 2001, 10(3): 234-253.

[10] SELESNICK I, BARANIUK R, KINGSBURY N. The Dual-tree Complex Wavelet Transform[J]. IEEE Signal Processing Magazine, 2005, 22(6): 123-151.

[11] 胥永刚, 孟志鹏, 陆明, 等. 双树复小波和奇异差分谱在滚动轴承故障诊断中的应用[J]. 振动工程学报, 2013, 26(6): 965-973. XU Yonggang, MENG Zhipeng, LU Ming, et al. Application of Double Tree Complex Wavelet and Singular Difference Spectrum in Fault Diagnosis of Rolling Bearings[J]. Journal of Vibration Engineering, 2013, 26(6): 965-973. (in Chinese)

[12] 李辉, 郑海起, 唐力伟. 基于改进双树复小波变换的轴承多故障诊断[J]. 振动、测试与诊断, 2013, 33(1): 53-59. LI Hui, ZHENG Haiqi, TANG Liwei. Multi-fault Diagnosis of Bearings Based on Improved Double Tree Complex Wavelet Transform[J]. Vibration, Test and Diagnosis, 2013, 33(1): 53-59. (in Chinese)

[13] 梁月吉, 任超, 杨秀发, 等. 结合双树复小波和广义回归神经网络的钟差预报方法研究[J]. 测绘通报, 2016(1): 6-10. LIANG Yueji, REN Chao, YANG Xiufa, et al. Research on Clock Error Prediction Method Combining Double Tree Complex Wavelet and Generalized Regression Neural Network[J]. Surveying and Mapping Bulletin, 2016(1): 6-10. (in Chinese)

[14] 张美英, 何杰. 时间序列预测模型研究综述[J]. 数学的实践与认识, 2011, 41(18): 189-195. ZHANG Meiying, HE Jie. Review of Research on Time Series Prediction Models[J]. Mathematics Practice and Cognition, 2011, 41(18): 189-195. (in Chinese)

[15] 潘迪夫, 刘辉, 李燕飞. 基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J]. 电网技术, 2008(7): 82-86. PAN Difu, LIU Hui, LI Yanfei. Wind Speed Forecast Optimization Model for Wind Farm Based on Time Series Analysis and Kalman Filter Algorithm[J]. Power Grid Technology, 2008(7): 82-86. (in Chinese)

[16] 王燕. 应用时间序列分析[M]. 北京: 中国人民大学出版社, 2012. WANG Yan. Applied Time Series Analysis[M]. Beijing: Renmin University of China Press, 2012. (in Chinese)

[17] 何书元. 应用时间序列分析[M]. 北京: 北京大学出版社, 2003. HE Shuyuan. Applied Time Series Analysis[M]. Beijing: Peking University Press, 2003. (in Chinese)

[18] 王志信, 黄鹏, 林友明, 等. 面向遥感卫星数据获取应用的时间序列云量预测方法[J]. 遥感信息, 2014, 29(3): 8-13. WANG Zhixin, HUANG Peng, LIN Youming, et al. Time Series Cloudiness Prediction Method for Remote Sensing Satellite Data Acquisition Application[J]. Remote Sensing Information, 2014, 29(3): 8-13. (in Chinese)

[19] LIU H, Mi X, LI Y. Wind Speed Forecasting Method Based on Deep Learning Strategy Using Empirical Wavelet Transform, Long Short Term Memory Neural Network and Elman Neural Network[J]. Energy Conversion and Management, 2018, 156: 498-514.

[20] 时小虎, 梁艳春, 徐旭. 改进的Elman模型与递归反传控制神经网络[J]. 软件学报, 2003(6): 1110-1119. SHI Xiaohu, LIANG Yanchun, XU Xu. Improved Elman Model and Recursive Backpropagation Control Neural Network[J]. Journal of Software, 2003(6): 1110-1119. (in Chinese)

[21] SHI X, LIANG Y, LEE H, et al. Improved Elman Networks and Applications for Controlling Ultrasonic Motors[J]. Applied Artificial Intelligence, 2004, 18(7): 603-629.

[22] 任丽娜. 基于Elman神经网络的中期电力负荷预测模型研究[D]. 兰州: 兰州理工大学, 2007. REN Lina. Research on Medium Term Load Forecasting Model Based on Elman Neural Network[D]. Lanzhou: Lanzhou University of Technology, 2007. (in Chinese)

[23] 韩旭明. Elman神经网络的应用研究[D]. 天津: 天津大学, 2006. HAN Xuming. Applied Research of Elman Neural Network[D]. Tianjin: Tianjin University, 2006. (in Chinese)

Cloud Time Series Combination Model Prediction Based on Dual-tree Complex Wavelet Decomposition

BAI Yunbo1,2OUYANG Sida2YANG Mengmeng3XIA Xueqi1WANG Ting4

（1 China University of Geosciences, Beijing 100083, China）（2 Land Satellite Remote Sensing Application Center, Beijing 100048, China）（3 Shandong University of Science and Technology, Qingdao 266590, China）（4 Chengdu University of Technology, Chengdu 610059, China)

Aiming at the problems of poor practicability, poor fitting effect and low accuracy of the traditional cloud prediction model when applied to cloud time series data of high-resolution satellite images, a cloud time series combination model prediction method based on dual-tree complex wavelet decomposition is proposed. The method uses DT-CWT decomposition method to extract low-frequency trend information and high-frequency random information of cloud amount time series, applies time series analysis and Elman neural network prediction methods to low-frequency and high-frequency sequences respectively, and then reconstructs the prediction results of the two sequences to obtain the final cloud amount prediction results. The experimental results show that the low-frequency information decomposed by dual-tree complex wavelet can better reflect the change trend of cloud cover, and the high-frequency information can also better retain the random information of cloud cover change. Compared with the traditional prediction model, the average absolute error and root mean square error of the prediction results of this method are reduced, the prediction accuracy is improved, and the change rule of high-resolution satellite cloud cover time series can be better fitted. The results of cloud cover prediction are taken as reference information in satellite imaging mission planning, and a smaller time window covered by cloud cover can be selected to obtain satellite effective imaging data with higher quality.

high resolution image; dual-tree complex wavelet decomposition; time series analysis; neural network; forecast of cloud volume by satellite remote sensing; remote sensing payload

TP79

A

1009-8518(2019)05-0106-12

白云博, 欧阳斯达, 杨朦朦, 等. 基于双树复小波分解的云量时间序列模型预测[J]. 航天返回与遥感, 2019, 40(5): 106-117.

BAI Yunbo, OUYANG Sida, YANG Mengmeng, et al. Cloud Time Series Combination Model Prediction Based on Dual-tree Complex Wavelet Decomposition[J]. Spacecraft Recovery & Remote Sensing, 2019, 40(5): 106-117. [DOI: 10.3969/j.issn.1009- 8518.2019.05.011]

白云博，男，1994年生，中国地质大学（北京）地质工程硕士在读研究生，主要研究方向为遥感数据存储与挖掘，大数据分析。E-mail：jackbaiyun@126.com。

欧阳斯达，男，1986年生，2011年获中国测绘科学研究院地图制图学与地理信息工程专业硕士学位，工程师。主要研究方向为测绘卫星任务计划与调度、测绘卫星影像数据管理与应用等。E-mail：ouyangsd@sasmac.cn。

2019-07-19

陆地卫星测绘类产品生产技术与专题生产（2018YFB0504903）

（编辑：庞冰）