数形结合思想小学数学教学中的巧妙应用

王自豪 廖秀永 张伟

摘要： 在数学教学过程中，“数”与“形”是其中两个非常基本的概念，并且两者之间存在一定的联系。尤其是对于小学生而言，在数学课堂上利用数形结合思想可以将原本比较复杂的数学知识通过更简单的形式呈现出来，便于学生对数学知识进行更好的理解和掌握。

关键词：数形结合；小学数学；应用

数形结合是指通过数上构形或形中觅数来解决问题的一种思想方法。它既是一种重要的数学思想与方法，又是一种理解数学、学好数学的有效手段。我们在研究数的时候，往往要借助于形的直观来分析，使数更加清晰、透彻；在探讨形的时候，又往往离不开数的本质。因此，在小学数学教学中有机地渗透数形结合思想，通过寻找数与形之间的关系，能使疑惑概念、难解题目豁然开朗，迎刃而解。

一、观察——培养逻辑思维

1.观察数形目的明确。小学生喜欢观察，但不善于观察，盲目性较大。所以在观察前，他们明确观察目的，才会集中注意力，才能收到预期的教学效果。如在教学用割补法推导平行四边形面积计算方法时，演示教具前，教师应提醒学生观察：①平行四边形变成了什么图形 ？ ②底和高的长度变了没有 ？ ③平行四边形的高和长方形的宽，底和长方形的长有什么关系 ？ 通过演示和观察，学生会很容易理解平行四边形的面积计算公式。

2 观察数形本质特征。学生观察时，常常被一些非本质的表象吸引，教师要引导学生观察几何形体的特征，捕捉其本质属性。为加深学生对平行四边形特征的认识和比较平行四边形与长方形的异同，可以拉动长方形活动教具进行演示。拉动长方形的对角，让学生观察边和角的变化，经过演示和观察，学生可发现：拉动长方形的对角，长方形就变成了平行四边形，两组对边分别平行且相等，内角和是 360°，它和长方形的不同点在于四个角不是直角。再让学生观察日常所见铁拉门格子的实例，学生就易理解平行四边形的可变特性。

另外，教学时须提供各种变式，不断变化其非本质属性，保证其本质属性，帮助学生认识图形的基本特征。例如，“只有一组对边平行的四边形是梯形”。至于这组平行的对边的长短、位置，梯形的大小、形状等则是非本质的。因此，要出示不同的图形，让学生辨认，掌握其特征。

二、计算——助力智力发展

（一） 以形助数

所谓“以形助数”，是指老师在讲解某些数学知识的时候，仅靠数字讲解学生不太能理解。借助几何图形的特点，将所要讲的知识点更直观地展现在学生面前。从而将抽象化的问题转变为具体化的问题。

例1如：一辆汽车从甲地开往乙地，先是经过上坡路，然后是平地，最后是下坡路，汽车上坡速度是每小时20千米，在平地的速度是每小时30千米，而下坡的速度则是每小时40千米，汽车从甲地到乙地一共上坡花了6小时，平地花了2小时，下坡花了4小时。请问汽车从乙地到甲地需要多长时间？

在这道题中，既存在变量，又存在不变量。变量就是上坡路和下坡路随着汽车行驶的方向而发生改变，当汽车从乙地到甲地行驶时，原先的上坡路变成了下坡路，原先的斜坡路变成了上坡路。而不变量就是这两个路程汽车行驶的速度都是始终不变的。因此老师在帮助学生解决这道题的时候。可以采用图形的形式解决，具体如下图所示：

那么在解决问题的时候，就可以直观地展现出来。先算出汽车从乙地到甲地的上坡时间，即（40×4）÷20=8（小时），然后算出下坡所花费的时间，即（20×6）÷40=3（小时），而平地所花费的时间是不变的，所以汽车从乙地到甲地所花费的时间是8+3+2=13（小时）。在这道题中，运用图像将数学中的数量关系、运算都直观地展现出来。学生比較易于理解，这样的教学可以在很大程度上提高教学效率。

（二） 以数助形

为了能够让学生真正认识数学结合思想，教师应遵从“以数助形”教学原则，让学生能够透过图形掌握其内在数学信息，慢慢养成良好的数学问题解题思维。例如，在《解直角三角形及其应用》一课教学时，教师可采取“以数助形”教学方法，指导学生结合直角三角形角与线段之间、线段之间位置关系和数量关系，进行“形”到“数”的转换，准确计算出图形中的数量关系。再如，在《多边形及其内角和》一课教学时，教师也可指导学生透过多边形特殊性分析其中数量关系。

例2：已知有一块长与宽分别是am和bm的草坪，现在要在这块草坪上修筑一条小路，假设这条小路的宽是1m，余下草坪用m2表示。那么若想增加美感，把原有小路设计为一条宽为1m的弯曲小路，余下草坪面积是多少？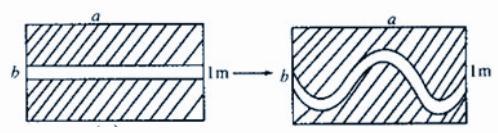

教师在带领学生解决这一道数学问题时，可先为学生出示相应的图示，带领学生透过图示分析题目本质，了解题目考察的重点内容是矩形面积问题，利用矩形面积=长×宽这个公式，快速求解出正确答案。在上述案例教学中，教师要带领学生先分析图示的特殊性，引导学生通过平移图示发现一个新的矩形，进而通过由“形”到“数”的转换，快速求出相应答案。

综上所述，通过对数形结合思想的有效运用，不但可以改变枯燥无聊的课堂氛围，同时在一定程度上还能不断带动学生对于数学课程学习的积极性，使学生在面对问题时可以很快地进行解决。因此，我们应积极地在数学教学中探索数形结合思想的渗透应用方法，从而全面提升教学效果。

参考文献

[1]季晶.数形渗透思维开花——浅谈小学数学教学中数形结合思想渗透策略[J].小学教学参考， 2014（3）

[2]李玉媛.数形结合思想在小学数学教材中的渗透[J].考试周刊，2013（58）