笼型转子无刷双馈发电机的间接功率控制
2019-11-04赵荣理张爱玲田慕琴闫珺马赟
赵荣理 张爱玲 田慕琴 闫珺 马赟


摘要关键词:无刷双馈电机;笼型转子无刷双馈发电机;间接功率控制;有功功率;无功功率
DOI:10.15938/j.emc.2019.09.001
中图分类号文献标志码:A文章编号:1007-449X(2019)09-0001-08
收稿日期基金项目作者简介:
通信作者:赵荣理Indirect power control strategy for brushless
doubly fed induction generator
ZHAO Rong li1,ZHANG Ai ling1,TIAN Mu qin1,YAN Jun2,MA Yun3
(1.College of Electrical and Power Engineering, Taiyuan University of Technology, Taiyuan 030024, China;
2.State grid Taiyuan Power Supply Company, Taiyuan 030012, China;
3.State grid Jinzhong Power Supply Company, Jinzhong 030600, China)
Abstract:An indirect power control strategy was proposed for the brushless doubly fed induction generator (BDFIG) to realize active and reactive power control separately after it was connected to the grid, to resolve the issue that output of BDFIG should be controlled in the variable speed constant frequency wind power generation system. The analytic relationship of active power with the dynamic phase increment and amplitude increment of the control wind flux linkage vector was derived in detail by using unified reference frame dq model of BDFIG. Active and reactive power controllers were designed based on theoretical analysis and then the structure diagram of control system was established. Experimental results of the prototype show the active power and reactive power are controlled. In this presented scheme, the system structure is simple without rotating coordinate transformation and less machine parameters are needed.
Keywords:brushless doubly fed machine; brushless doubly fed induction generator; indirect power control; active power; reactive power
0引言
和雙馈电机(doubly fed induction generator, DFIG)相比,无刷双馈电机(brushless doubly fed machine, BDFM)由于没有电刷和滑环,大大提高了工作可靠性,降低了维护工作量,所以在变速恒频风力发电系统具有广阔的应用前景。BDFM的结构特殊,定子上有两套相互独立的不同极数的三相对称绕组,即功率绕组和控制绕组,控制绕组由变频器供电,功率绕组与电网相连。两套定子绕组共用一个铁心,没有直接的电磁耦合,而是通过转子绕组的调制作用间接地进行能量的传递。常见的转子结构有两种,一种为磁阻转子,另一种为笼型转子,又叫做无刷双馈感应电机(brushless doubly fed induction machine, BDFIM)。本文的研究对象是笼型转子无刷双馈发电机(brushless doubly fed induction generator, BDFIG)。
近年来,无论是BDFM本体的优化设计还是其数学模型和控制策略,都取得了令人瞩目的研究成果。优化设计方面,在转子结构优化[1-4]、增强定转子耦合能力、减小谐波和温升、提高电机力能指标[5-7]方面取得了一系列突破和进展。数学模型方面,多回路模型[8]、两轴模型[9-10]、尤其是统一坐标系模型[11]的建立,为控制策略的研究提供了极大的方便。
由于BDFM结构和数学模型的特殊性,并不能将DFIG的控制方法拿来就用,必须另辟蹊径。近年来此电机的矢量控制技术[12-15]、直接转矩控制技术[16-17]、智能控制技术[18-19]及间接转矩控制技术[21-22]等取得了大量的研究成果,其中文献[12-13]提出了BDFIG功率绕组磁链定向的矢量控制技术,前者系统结构复杂,后者虽然系统结构简单,但是没有电流内环,系统缺乏限流保护功能,并在一定程度上影响了系统的动态性能。经过几年的发展,文献[14]中控制系统的结构在形式上和DFIG的矢量控制系统已十分相似,系统以功率绕组输出的有功功率和无功功率作为外环,控制绕组电流作为内环,取得了较为满意的动、静态性能,但是也需要旋转坐标变换和磁场定向。文献[21-22]提出了BDFIG的间接转矩控制方法,该方法将电机转速及无功功率作为系统的控制信号,取得了较好的控制效果。
现阶段变速恒频风电系统实现最大功率点跟踪控制有四种有效的方法[20]:最佳叶尖速比法,最优转矩法,功率反馈法和爬山法,其中功率反馈法根据厂家提供的风机输出功率与转速曲线,将风机输出的最大功率作为发电机的功率给定,以实现最大功率点跟踪控制。为了适应风电系统的应用需要,本文提出了一种BDFIG的间接功率控制方法,该方法将功率绕组输出的有功功率和无功功率作为控制信号,推导了有功功率和控制绕组磁链矢量动态相位增量和幅值增量之间的解析关系,在此基础上设计了有功功率和无功功率控制器,构建了无刷双馈发电机间接功率控制系统的结构框图。样机的实验结果证明了所提控制方法的可行性。
1无刷双馈电机控制绕组磁链的空间矢量图1是控制绕组磁链空间矢量ψ→c(t)的运动轨迹,如图所示,每经过一个采样周期,控制绕组磁链就前进一步,如由ψ→c(k-1)变为ψ→c(k)。分别用ks(k)和ΔXc(k)表示控制绕组磁链在一个采样周期的幅值和相位增量,其中ΔXc(k)由静态相位增量ΔXst(k)和动态相位增量ΔXd(k)组成,即
ΔXc(k)=ΔXst(k)+ΔXd(k)。(1)
1.1静态相位增量的计算
无刷双馈电机的转速表达式为
n=60(fp+fc)pp+pc。(2)
式中:n为转速;f为频率;p为极对数;下标p、c分别表示功率绕组和控制绕组变量,例如,fc为控制绕组频率,fc>0时为超同步运行状态,fc<0时为亚同步运行状态。
由式(2)可得控制绕组频率表达式为
fc=n(pp+pc)60-fp。(3)
则静态相位增量为
ΔXst=2πfcTpwm。(4)
式中TPWM表示采样周期。
1.2控制绕组磁链增量的计算
从图1可得,控制绕组磁链增量可表示为
Δψ→c(k)=ψ→c(k)-ψ→c(k-1)。(5)
用ks(k)和ΔXc(k)表示
Δψ→c(k)=[ejΔXc(k)(1+ks(k))-1]ψ→c(k-1)。(6)
利用欧拉公式,式(6)可写成
Δψ→c(k)=Δψαc(k)+jΔψβc(k)。(7)
式中:Δψαc和Δψβc分别为控制绕组磁链增量的α, β分量,表达式分别为[21]
Δψαc(k)=ψαc(k-1)[(1+ks(k))cosΔXc(k)-1]-
(1+ks(k))ψβc(k-1)sinΔXc(k),
Δψβc(k)=ψβc(k-1)[(1+ks(k))cosΔXc(k)-1]-
(1+ks(k))ψαc(k-1)sinΔXc(k)。(8)
由式(8)可知,由ks(k)和ΔXc(k)可以计算第k个采样周期控制绕组的磁链增量。
2BDFIM的数学模型
为了推导有功功率、无功功率与控制绕组磁链关系的表达式,本文采用了统一坐标系的控制绕组静止坐标系模型,其电压和磁链方程[11]如(9)~式(14)所示:
ψ→p=Lpi→p+Lhpi→r,(9)
ψ→c=Lci→c+Lhci→r,(10)
ψ→r=Lhpi→p+Lhci→c+Lri→r,(11)
u→p=Rpi→p+dψ→pdt-j(pp+pc)ωrψ→p,(12)
u→c=Rci→c+dψ→cdt,(13)
u→r=0=Rri→r+dψ→rdt-jpcωrψ→r。(14)
式(9)~式(14)中: i→,u→和ψ→为电流,电压和磁链矢量;下标r表示转子绕组的变量;R为电阻;Lhp,Lhc分别为功率绕组、控制绕组和转子之间的耦合电感;Lp,Lc和Lr为自感;ωr为转子机械角速度。
在控制绕组静止坐标系,功率绕组有功功率和无功功率可以表示为
Pp=32Re(u→pi→*p),(15)
Qp=32Im(u→pi→*p)。(16)
3BDFIM间接功率控制系统的结构框图3.1有功功率与无功功率控制器的设计
由式(9)~式(14),可得功率绕组电流为[22]
i→p=-LhcLhpψ→c+(LcLr-L2hc)ψ→pLcL2hp+LpL2hc-LcLpLr。(17)
式(12)中忽略电阻压降,可得
u→p≈dψ→pdt-j(pp+pc)ωrψ→p。(18)
將ωr=ωp+ωcpp+pc代入式(18),得:
ψ→p=1ωpu→pejπ2。(19)
式中:ωp为功率绕组角频率;ωc为控制绕组角频率。
将式(17),式(19)代入式(15), 则功率绕组的有功功率可表示为
pp=32Re(u→pi→*p)=
-32A1ReLhcLhpu→pψ→*c+A21ωpu→pe-jπ2u→*p。(20)
将式(20)离散后可得
Pp(k)=-32A1ReLhcLhpu→p(k)ψ→*c(k)+
A21ωpu→p(k)e-jπ2u→*p(k)。(21)
式中, A1=1LcL2hp+LpL2hc-LcLpLr,
A2=(LcLr-L2hc)。
参考式(6),式(21)中的ψ→*c(k)可以写成:
ψ→*c(k)=e-jΔXc(k)(1+ks(k))ψ→*c(k-1)。(22)
式(21)中的功率绕组电压也可写为
u→p(k)=ejΔXpc(k)u→p(k-1)。(23)
式中,ΔXpc(k)为功率绕组电压相位增量,且ΔXpc(k)=ΔXst(k)。
将式(22),式(23)代入式(21),且考虑到
u→p(k-1)ψ→*c(k-1)=|u→p(k-1)|
|ψ→c(k-1)|
ej(ΔXpc(k-1)-ΔXc(k-1))=
|u→p(k-1)|
|ψ→c(k-1)|e-jΔXd(k-1)。
则式(21)可化简为
Pp(k)=-32A1ReLhcLhp(1+ks(k))
u→p(k-1)ψ→*c(k-1)×
ej(ΔXpc(k)-ΔXd(k)-ΔXst(k))-
jA21ωp|u→p|2(k-1)=
-32A1[LhcLhp(1+ks(k))
|u→p(k-1)||ψ→c(k-1)|
cos(ΔXd(k-1)+ΔXd(k))]。(24)
因为式(24)中的ΔXd很小,所以式(24)可化简为:
Pp(k)=-32A1[LhcLhp|u→p(k-1)|
|ψ→c(k-1)|×
(cosΔXd(k-1)-
ΔXd(k)sinΔXd(k-1)+
ks(k)cosΔXd(k-1))]=
-C(cosΔXd(k-1)-
ΔXd(k)sinΔXd(k-1)+
ks(k)cosΔXd(k-1))。(25)
式中,C=32A1[LhcLhp|u→p(k-1)||ψ→c(k-1)|]。
同理,第k-1个采样周期有功功率表达式为
Pp(k-1)=-32A1Re[LhcLhpu→p(k-1)ψ→*c(k-1)+
A21ωpu→p(k-1)e-jπ2u→*p(k-1)=
-CcosΔXd(k-1)。(26)
考虑式(25)和式(26),则
Pp(k)=Pp(k-1)+ΔPp(k)=
Pp(k-1)+K1(k-1)ΔXd(k)+
K2(k-1)ks(k)。(27)
ΔPp(k)=K1(k-1)ΔXd(k)+K2(k-1)ks(k),
K1(k-1)=CsinΔXd(k-1),
K2(k-1)=-CcosΔXd(k-1)。(28)
式中:ΔPp(k)是第k个采样周期有功功率的增量。
按照相同的方法,可得第k个和第k-1个采样周期无功功率关系为
Qp(k)=Qp(k-1)+ΔQp(k)=Qp(k-1)-
K2(k-1)ΔXd(k)+K1(k-1)ks(k),
ΔQp(k)=-K2(k-1)ΔXd(k)+K1(k-1)ks(k)。(29)
式中:ΔQp(k)是第k个采样周期无功功率的增量。
式(27)~式(29)表明,通过对ΔXd(k)和ks(k)的控制可以实现BDFIG功率绕组输出有功及无功功率的控制。
3.2BDFIG间接功率控制系统的结构框图
式(27)~式(29)为BDFIG间接功率控制方法的基本方程式,基于这组方程式可以得到有功及无功功率控制的方框图如图2 所示。图中用到3个PI调节器,即有功、无功功率及磁链PI调节器。其中有功功率PI调节器的输出为控制绕组磁链的动态相位增量ΔXd,将其与静态相位增量ΔXst相加后为ΔXc。无功功率PI调节器的输出为控制绕组磁链幅值|ψ→c|*,磁链PI调节器的输出为控制绕组磁链的幅值增量ks[22]。
基于图2可以画出BDFIG间接功率控制系统框图如图3所示,图中,由ks和ΔXc可算出控制绕组磁链增量Δψαc和Δψβc(见式(8)),从而得到控制绕组电压分量uαc和uβc控制逆变器,如式(30)所示。
uαc=ΔψαcTpwm+Rciαc,
uβc=ΔψβcTpwm+Rciβc。(30)
3.3功率和磁链的观测
如图3所示,系统中需要观测BDFIG功率绕组的有功,无功功率和控制绕组磁链。
有功和无功功率的观测可通过功率绕组的电压和电流分量进行计算,在此不再赘述。实验中,采用改进的u-i模型—非线性正交反饋补偿方法[23]观测控制绕组的磁链,较好地解决了u-i模型积分漂移与低频运行时磁链观测不准确的问题。
4实验及结果分析
4.1实验平台简介
实验所用的BDFIG样机参数为:功率绕组极对数pp=3,控制绕组极对数pc=1,即同步速为750 r/min,转子为笼型。功率绕组额定功率PpN=3 kW,控制绕组额定功率PcN=1.5 kW,Rp=3.2 Ω,Rc=5.32 Ω,Rr=0.173 mΩ,Lp=292 mH,Lc=642 mH,Lr=0.048 mH,Lhp=2.16 mH,Lhc=4 mH,转动惯量为J=0.064 kg·m2。
图4是实验装置。BDFIG由一台额定功率为2.2 kW的异步电动机拖动,异步电动机由西门子MICROMASTER440系列的变频器进行控制。BDFIG的功率绕组接电网,控制绕组接双向变流器。其中控制绕组侧变流器以DSP芯片TMS320LF2407A为控制核心,其通讯接口CAN及PC机的USB接口通过USBCAN接口卡相连,实现DSP与PC机之间的数据交换。
4.2实验结果及分析
4.2.1变速恒频发电实验
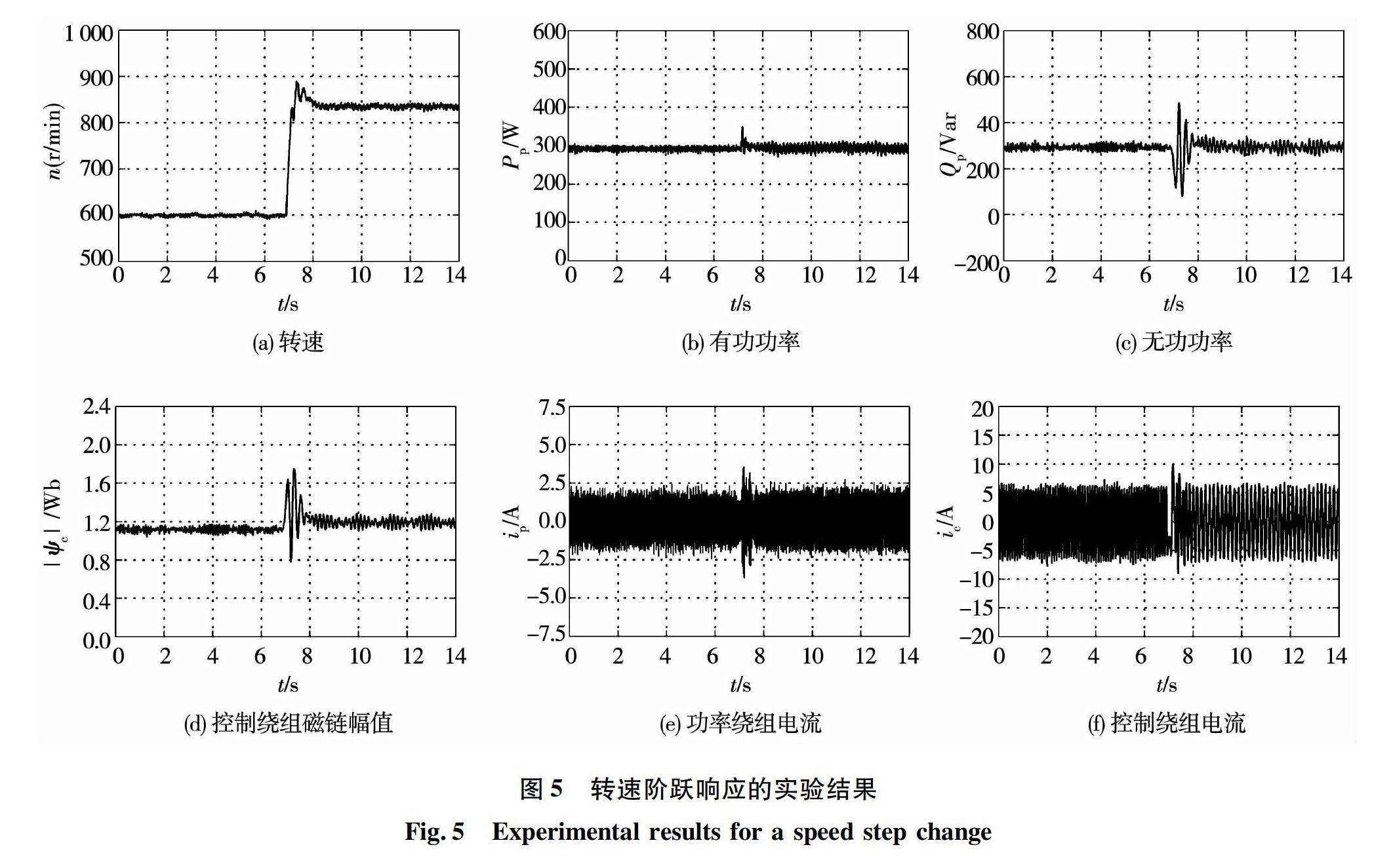
BDFIG发电并网后进行间接功率控制,保持有功功率给定值为300 W,无功功率给定值为300 var不变,用异步电动机将BDFIG由600 r/min(亚同步状态,fc=-10 Hz)阶跃变化至840 r/min(超同步状态,fc=6Hz)的实验结果如图5所示。
图5(a)为转速反馈波形,上升时间约1 s。图5(b)和5(c)为有功功率及无功功率反馈波形,在转速变化的动态过程中,二者都受到影响,但经过短暂的调节后均回到给定值附近,其中无功功率的调节时间略长,约1.2 s。图5(d)为控制绕组的磁链幅值,为了维持无功功率不变,控制绕组的磁链幅值经过调整后增加到1.2 Wb。图5(e)和5(f)分别为功率绕组和控制绕组电流波形,功率绕组电流频率保持50 Hz不变,而控制绕组电流频率随转速改变而改变,从10 Hz变至6 Hz。图5的实验结果表明,本文提出的BDFIG的间接功率控制方法可以实现变速恒频发电,且系统运行稳定。
4.2.2有功功率的斜坡响应
用异步电动机将BDFIG拖动到600 r/min(亚同步状态,fc=-10 Hz),保持无功功率给定值为0不变,将有功功率给定值从0斜坡变化到800 W,实验结果如图6所示。
图6(a)为有功功率反馈波形,紧跟给定值变化,上升时间约为2 s,无超调。图6(b)所示为无功功率反馈波形,动态过程受到影响,但是在无功PI调节器的调节下,很快又回到给定值0附近。转速最大动态降落为10%,经西门子变频器调节后重新回到600 r/min,如图6(c)所示。为了维持无功功率不变,控制绕组的磁链幅值由0.85 Wb增加到1.1 Wb。由于有功功率和磁链幅值的增加,功率绕组和控制绕组的电流幅值也随之增加,但频率都保持不变。如图6(e)~6(f)所示。图6的实验结果表明本文提出的控制方法能够实现无刷双馈发电机有功功率的动态调节和控制,且当有功功率变化时,无功功率的动态过程虽然受到影响,但是无功PI调节器有调节的能力。
4.2.3无功功率的阶跃响应
用异步电动机将BDFIG拖动到840 r/min(超同步状态,fc=6 Hz),保持有功功率给定值为200 W不变,将无功功率给定值从400 Var阶跃变化到-100 Var的实验结果如图7所示。
图7(a)为有功功率反馈波形,跟随给定保持不变。图7(b)所示为无功功率反馈波形,紧跟给定值变化,下降时间约为1 s,超调量为3%。图7(c)为转速波形,在动态过程中转速受到影响,达到稳态后又回到840 r/min。图7(d)为控制绕组的磁链幅值,当无功给定值从感性400 Var阶跃变化到容性100 Var时,控制绕组的磁链幅值由1.2 Wb减小到1.05 Wb。由于功率绕组有功功率保持不变,功率因数增加,因此其电流幅值减小,如图7(e)所示。控制绕组电流幅值也减小是由于无功功率从感性变为容性,如图7(f)所示。图7的实验结果表明在无功功率调节的动态过程中系统运行稳定。
5结论
本文提出了一种BDFIG的间接功率控制方法,该方法以功率绕组输出有功功率及无功功率作为控制变量。样机的实验结果表明该方法不仅能够实现有功功率与无功功率的闭环调节,并且能够实现变速恒频发电控制。
和矢量控制相比,该方法不需旋转坐标变换和磁链定向,系统结构简单,且用到的电机参数仅仅为控制绕组的电阻,系统的鲁棒性较强。
参 考 文 献:
[1]龚晟,杨向宇,纪梁洲.凸极转子无刷双馈电机的电感参数计算及转子设计[J]. 电机与控制学报, 2013, 17(2):78.
GONG Sheng,YANG Xiangyu,JI Liangzhou. Inductance calculation of reluctance rotor brushless doubly fed machine [J]. Electric Machines and Control,2013,17(2):78.
[2]XIONG F, WANG X F. Design of a low harmonic content wound rotor for the brushless doubly fed generator [J].IEEE Transactions on Energy Conversion,2014, 29(1):158.
[3]黃长喜, 阚超豪, 任泰安, 等.磁阻式无刷双馈电机的转子结构及性能分析[J].电工技术学报, 2017, 32(2):26.
HUANG Changxi, KAN Chaohao, REN Taian, et al. Performance analysis on brushless doubly fed motor with reluctance rotor [J]. Transactions of China Electrotechnical Society, 2017, 32(2):26.
[4]张凤阁, 王秀平, 贾广隆, 等.无刷双馈电机复合转子结构参数的优化设计[J].电工技术学报, 2014, 29(1):77.
ZHANG Fengge, WANG Xiuping, JIA Guanglong, et al. Optimum design for composite rotor structural parameters of brushless doubly fed machine [J]. Transactions of China Electrotechnical Society, 2014, 29(1):77.
[5]刘慧娟, XU L Y.一种径向叠片磁障式转子双馈无刷电机的设计与性能分析[J].电工技术学报, 2012, 27(7): 55.
LIU Huijuan, XU L Y. Design and performance analysis of a doubly excited brushless machine with radially laminated magnetic barrier rotor [J]. Transactions of China Electrotechnical Society, 2012, 27(7):55.
[6]张凤阁, 蒋晓东, 李应光.笼障转子无刷双馈电机水冷系统设计[J].电机与控制学报, 2018, 22(6): 70.
ZHANG Fengge, JIANG Xiaodong, LI Yingdong. Design of water cooling system of brushless doubly fed machine with cage barrier rotor [J]. Electric Machines and Control,2018,227(6):70.
[7]MCMAHON R A,ABDI E,MALLIBAND P,et al.Design and testing of a 250 kW medium speed brushless DFIG [C]// 6th IET International Conference on Power Electronics, Machines and Drives, 2012:1.
[8]WALLACE A K, SPEE R. Dynamic modeling of brushless doubly fed machine[C]//IEEE IAS Annual Meeting,San Diego,1989:329.
[9]LI R,WALLACE A K,SPEE R. Two axes model development of cage rotor brushless doubly fed machines [J]. IEEE Transactions on Energy Conversion,1991,6(3):444.
[10]BOGER M S,WALLACE A K.General pole number model of the brushless doubly fed machine[J].IEEE Transactions on Industry Application,1995,31(5):1022.
[11]POZA J, ROYE D, RODRIGUEZ M. Unified reference frame dq model of the brushless doubly fed machine [J]. IEE Proceedings Electric Power Application,2006,153(5):729.
[12]POZA J,OYARBIDE E,SARASOLA I,et al. Vector control design and experimental evaluation for the brushless doubly fed machine [J]. IET Electric Power Applications, 2009,3(4):249.
[13]SHAO S Y,ABDI E, BARATI F,et al. Stator flux oriented vector control for brushless doubly fed induction generator [J].IEEE Transactions on Industrial Electronics, 2009,56(10):4225.
[14]LONG T,SHAO S Y,MALLIBAND Paul,et al.Crowbarless fault ride through of the brushless doubly fed induction generator in a wind turbine under symmetrical voltage dips [J]. IEEE Transactions on Industrial Electronics,2013,60(7):2835.
[15]黃守道, 王耀南, 王毅, 等.无刷双馈电机有功和无功功率控制研究[J].中国电机工程学报, 2005, 25(4): 90.
HUANG Shoudao,WANG Yaonan,WANG Yi,et al.A study of active and reactive power control for brushless doubly fed machine [J]. Proceedings of the CSEE,2005,25(4):90.
[16]SARASOLA I,POZA J,RODRIGUEZ M A,et al. Direct torque control design and experimental evaluation for the brushless doubly fed machine [J]. Energy Conversion and Management, 2011, 52(2):1226.
[17]張爱玲,许永顺,王昕.直接转矩控制的无刷双馈感应电机的异步启动[J]. 电机与控制学报, 2012, 16(6):71.
ZHANG Ailing,XU Yongshun,WANG Xin. Asynchronous starting for BDFIM based on direct torque control strategy [J]. Electric Machines and Control,2012,16(6):71.
[18]张凤阁, 金石.无刷双馈风力发电系统的L2鲁棒控制[J]. 电机与控制学报, 2010, 14(8):70.
ZHANG Fengge,JIN Shi. L2 robust control for brushless double fed wind power generation system [J]. Electric Machines and Control,2010,14(8):70.
[19]陈亦哲, 杨俊华, 吴捷.无刷双馈风力发电系统模糊自抗扰最大风能捕获控制[J]. 电机与控制应用, 2010, 10(8):62-65,81.
CHEN Yizhe,YANG Junhua,WU Jie. Control of Maximum power point tracking of brushless doubly fed wind generator with fuzzy active disturbance rejection decoupling control [J]. Electric Machines & Control Application,2010,10(8):62-65,81.
[20]ABDULLAH M A,YATIM A H M,TAN C W,et al. A review of maximum power point tracking algorithms for wind energy systems [J]. Renewable and Sustainable Review,2012,16:3221.
[21]ZHANG A L,WANG X,JIA W X,et al. Indirect stator quantities control for the brushless doubly fed induction machine [J].IEEE Transactions on Power Electronics,2014,29(3):1394.
[22]ZHAO R L,ZHANG A L,MA Y,et al. The dynamic control of reactive power for the brushless doubly fed induction machine with indirect stator quantities control scheme [J].IEEE Transactions on Power Electronics,2015,9(30):5050.
[23]马赟, 许永顺, 王昕,等.无刷双馈感应电机直接转矩控制系统中的磁链观测方法[J].电机与控制应用, 2013, 40(8):31.
MA Yun,XU Yongshun,WANG Xin,et al. Flux estimating method for the brushless doubly fed induction motor based on direct torque control system [J]. Electric Machines & Control Application,2013,40(8):31.
