虹桥式木拱桥结构力学特性分析
2019-11-04孟雨泽宋郁民王思颖张泰源
孟雨泽, 宋郁民,王思颖,张泰源
(上海工程技术大学 城市轨道交通学院, 上海 201620)
木材具有取材容易,加工方便,重量轻,强度较高,抗震性能较好的优点,相较于石材,木材重量极轻,是建造桥梁最原始的材料之一[1-3]。其中,木拱桥在我国古代桥梁史占有极其重要的地位,它以独特的编木拱结构,利用两个纵桥向的拱肋系统相互交替有组织的编制在一起,再辅以若干横桥向的横木联结组成,形成拱形结构,实现了较大的跨度,且直木无需弯曲,节点处无需借助金属材料辅助连接,结构精巧,受力合理,施工简单[4-7]。然而,目前对虹桥式木拱桥的结构受力性能方面的研究较少,本文以一座虹桥式木拱桥为例,通过改变其拱肋的矢跨比、节间数和截面尺寸,分别建立与之相对应的有限元模型,并将有限元模型中的计算结果进行对比分析,研究上述三个因素的变化对于虹桥式木拱桥结构力学特性的影响。
1 工程背景
1.1 工程背景简介
该虹桥式木拱桥全长11.4 m,桥宽为2.1 m,桥面及栏杆向两侧路基延伸,全长21.6 m,主拱结构净跨径为9.584 m,净矢高为1.55 m,矢跨比为1/6.18,桥下正常水位-0.400 m。原桥型见图1。
该木拱桥的拱肋结构由两个系统相互交叉编织而成,并辅以横木,使两系统紧密结合,构成桥梁主拱结构的拱肋彼此之间用铆钉连接,既保证了一定的强度,也便于日后的维护修理,同时结构形式优美而流畅。原桥梁编木拱结构设计图见图2。
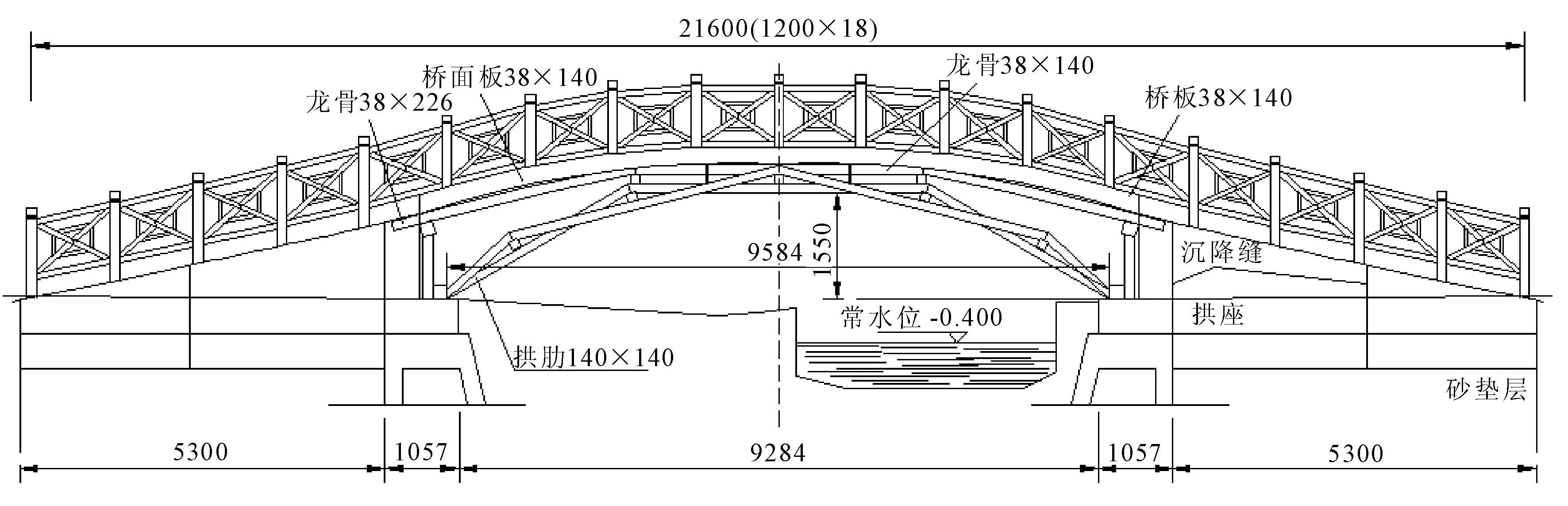
图1原桥型布置图(单位:mm)
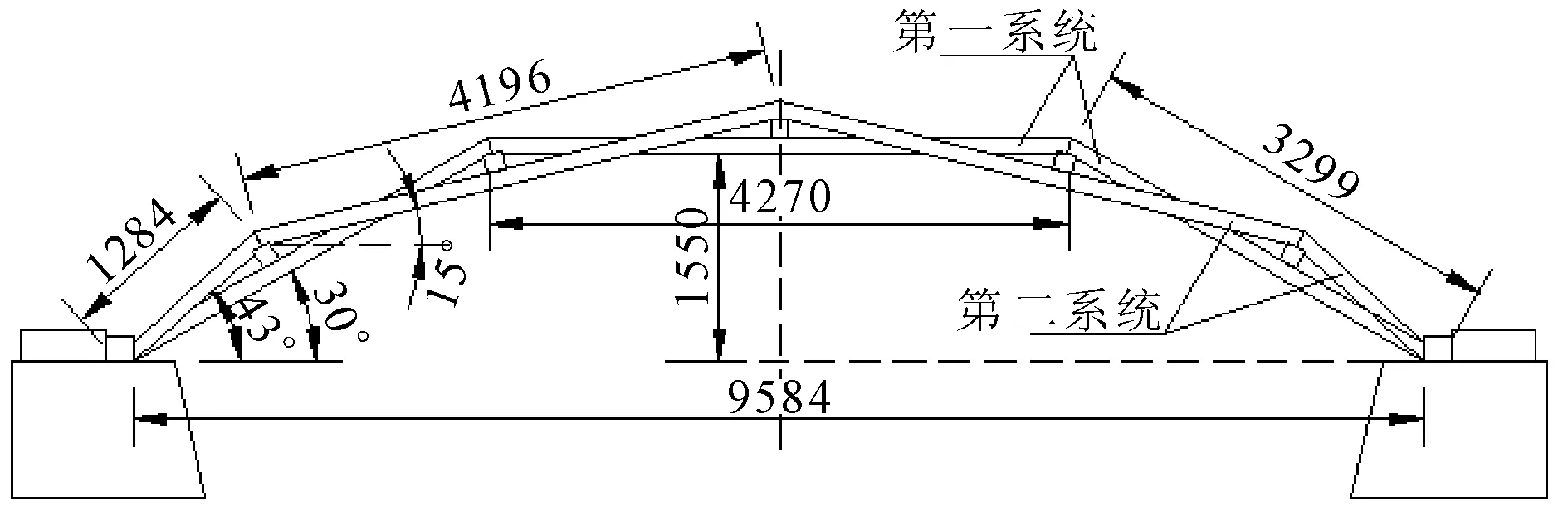
图2编木拱结构设计图(单位:mm)
本文以此木拱桥为原型,在原桥桥面板和栏杆等设施不变的情况,通过改变拱肋的矢跨比、节间数和截面尺寸,来研究编木拱结构最大应力和最大挠度的变化规律,以及在极限承载能力下,结构所能承受的最大荷载的变化规律。
1.2 材料特性和设计强度
木桥全桥均采用俄罗斯樟子松,根据《木结构设计规范》[8](GB 50005—2003),查得俄罗斯樟子松的木材强度等级属于TC13B,弹性模量E=9 000 MPa,顺纹抗压及承压极限为10 MPa,顺纹抗拉极限为8 MPa,抗弯强度设计值为13 MPa,泊松比取0.3,木材的质量密度取540 kg/m3。
2 力学特性分析
2.1 结构建模
拱肋结构采用MIDAS/Civil空间有限元程序进行建模验算,拱肋结构采用梁单元进行模拟。木材为各性异向材料,要精确模拟其材料的本构关系比较困难,此处我们只研究其纵向受力系统,因此用自定义各向同性材料来模拟俄罗斯防腐木材[1]。
拱脚用固定铰支座模拟,即约束三个线位移Dx、Dy、Dz,释放三个角位移Rx、Ry、Rz。拱肋与横梁之间采用铆钉连接,用弹性连接来进行模拟[1,9-10],弹簧刚度根据静载试验结果进行修正[1]。用较大的线刚度来约束y方向和z方向的线位移,用较小的线刚度来约束x方向的线位移;对拱肋与横梁x方向与z方向的转动刚度进行约束。因为不改变原桥的桥面板和栏杆等设施,所以将拱肋结构以上的结构自重(包括桥面板和护栏等附属设施)加上人群荷载以外荷载的形式作用在拱肋节点上。弹性连接具体取值见表1。

表1 拱肋与横梁弹性连接具体取值
(1) 矢跨比。根据工程背景,固定了虹桥式木拱桥拱肋结构跨度L=9.6 m,改变其矢跨比H/L,即改变拱肋结构的矢高H。本文分析研究四种不同矢跨比的模型,即矢跨比分别为1/6、1/5、1/4、1/3。因拱肋节点不随矢跨比的改变而发生变化,所以经计算不同矢跨比采用相同的节点荷载,即32.892 kN。各矢跨比参数见表2。
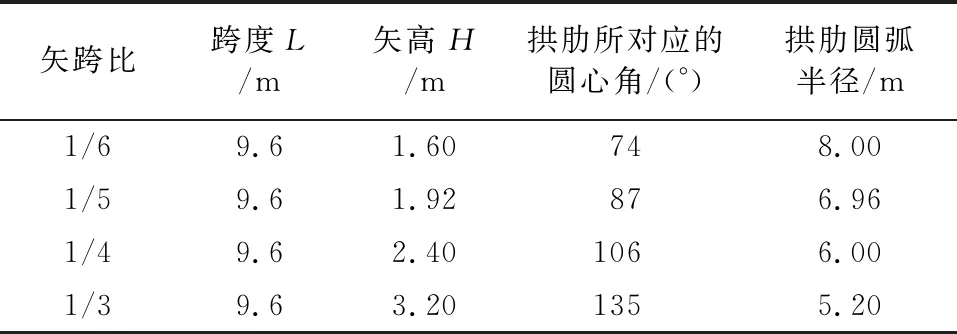
表2 不同矢跨比参数
(2) 节间数。为了增强不同节间数有限元模型的可比性与准确性,本文选用相同的矢跨比H/L=1/4,来讨论五种不同的节间数,即节间数分别为五节拱、六节拱、七节拱、八节拱和九节拱[11]。因节间数的改变,使得拱肋结构中的节点数也随之变化,有限元模型中对应的节点荷载也随之改变。不同节间数所受节点荷载见表3。

表3 不同节间数所受的节点荷载
(3) 拱肋截面。为了增强不同拱肋截面有限元模型的可比性与准确性,本文选用矢跨比H/L=1/4和七节拱来讨论四种不同的截面尺寸,各截面尺寸见表4。

表4 不同截面尺寸
(4) 荷载组合。采用承载能力极限组合:1.2(自重)+1.2(二期)+1.4(人群)
2.2 矢跨比分析
2.2.1 强度分析
在承载能力极限组合作用下,不同矢跨比所对应的拱肋最大应力值见表5。

表5 不同矢跨比所对应的拱肋最大应力值
不同矢跨比所对应的拱肋应力图如图3、图4、图5所示,不同矢跨比所对应的拱肋最大应力值的变化图如图6所示。
由上述计算结果比较,可以发现:随着拱肋结构矢跨比的增大,构件内最大应力值逐渐减小。
根据夹角与矢跨比的关系中可知:因为木拱桥结构由杆件相互搭接而成,在节点处的内力平衡需要满足杆件的几何关系,而内力主要有拱肋承担,那么拱肋与外力之间的夹角越大,拱肋内部产生的轴力也就越大[8],故随着矢跨比的增大,拱肋节点处的角度变小,拱肋内部所产生的最大压应力也随之变小。

图31/6矢跨比对应的拱肋应力图

图41/4矢跨比对应的拱肋应力图

图51/3矢跨比对应的拱肋应力图
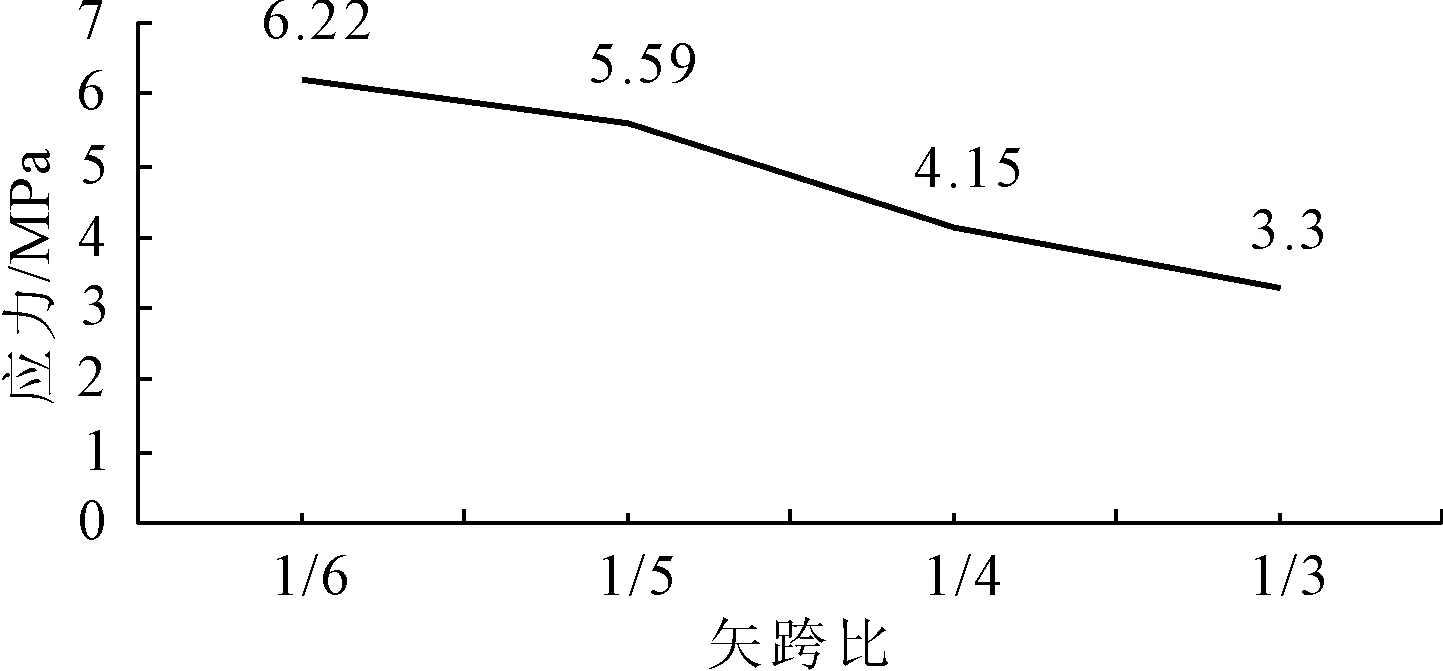
图6不同矢跨比对应的拱肋结构最大应力变化图
2.2.2 挠度分析
在承载能力极限组合作用下,不同矢跨比所对应的拱肋竖向挠度最大值见表6,表中竖向位移数值以竖直向下为正。

表6 不同矢跨比所对应的拱肋竖向挠度最大值
不同矢跨比所对应的拱肋竖向变形如图7、图8、图9所示,不同矢跨比所对应的拱肋竖向挠度最大值的变化图如图10所示。

图71/6矢跨比对应的拱肋竖向位移图
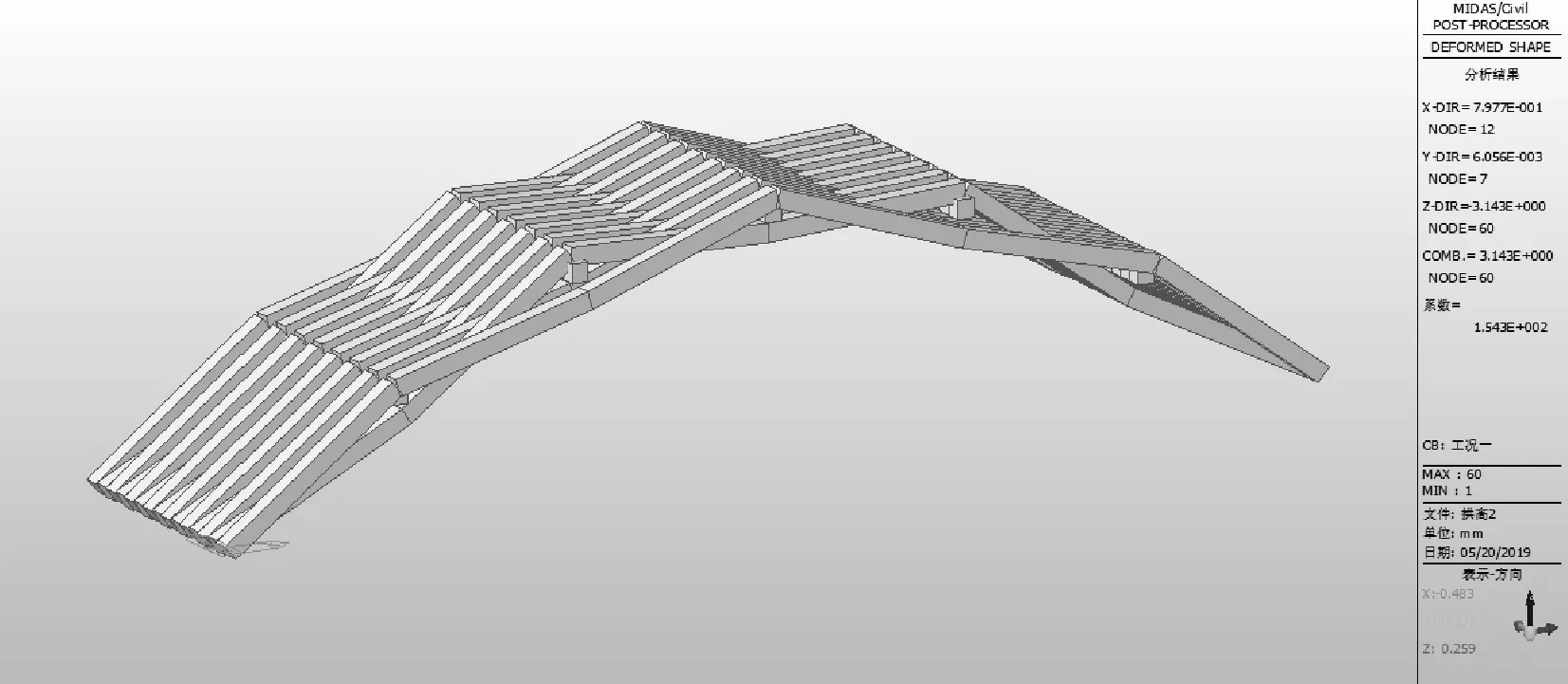
图81/4矢跨比对应的拱肋竖向位移图

图91/3矢跨比对应的拱肋竖向位移图
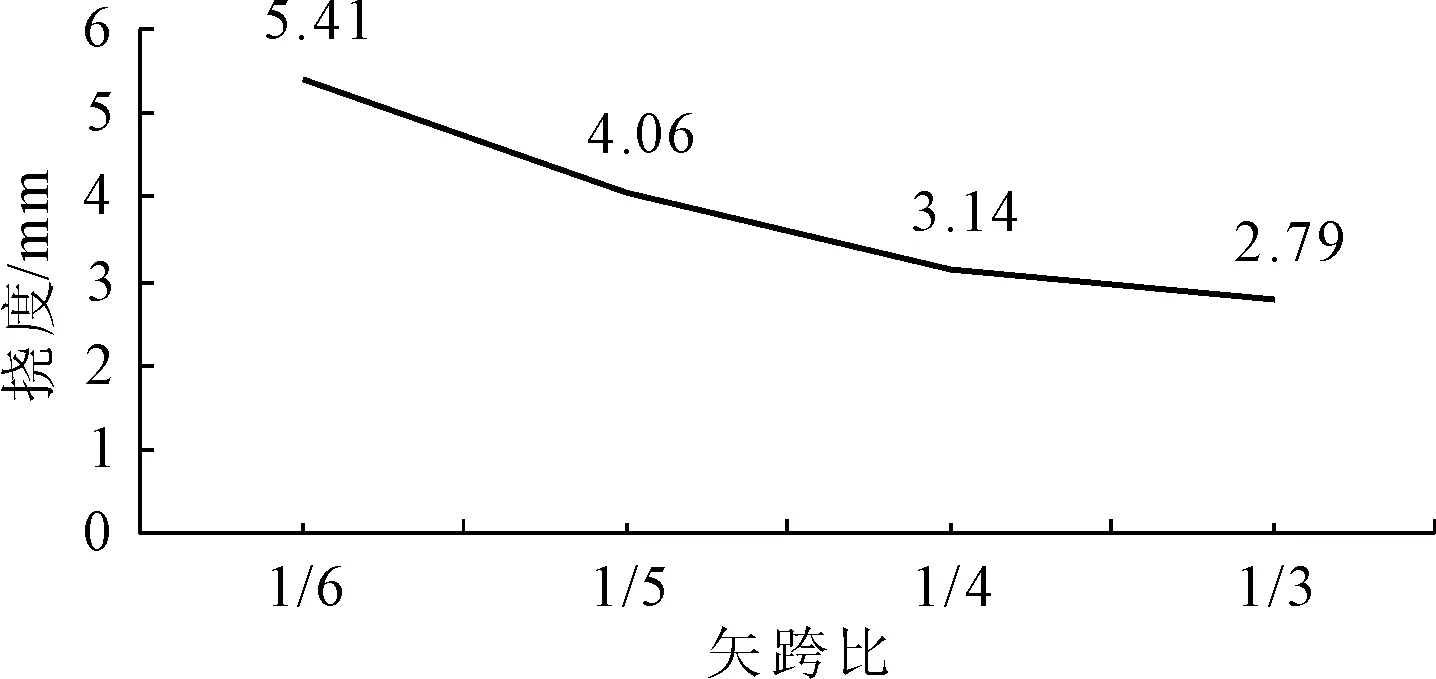
图10不同矢跨比对应的拱肋竖向挠度变化图
由上述计算结果比较,可以发现:随着拱肋结构矢跨比的增大,构件内最大挠度值逐渐降低。
由上文可知,随着矢跨比的增大,拱肋节点处的角度变小,拱肋内部所产生的最大压应力也变小,因压应力所产生的结构位移也随着变小。
2.2.3 极限承载能力分析
根据《城市人行天桥与人行地道技术规范》[12](CJJ 69—1995)中有关人行桥刚度应满足限制L/800=9 584 mm/800=11.98 mm的要求。拱肋结构达到极限承载能力状态时,拱肋最大应力、最大挠度及施加总荷载见表7。
从计算结果可以看出:当拱肋结构达到极限承载能力,随着拱肋结构矢跨比的增大,构件所能承受的总外荷载也不断增大。
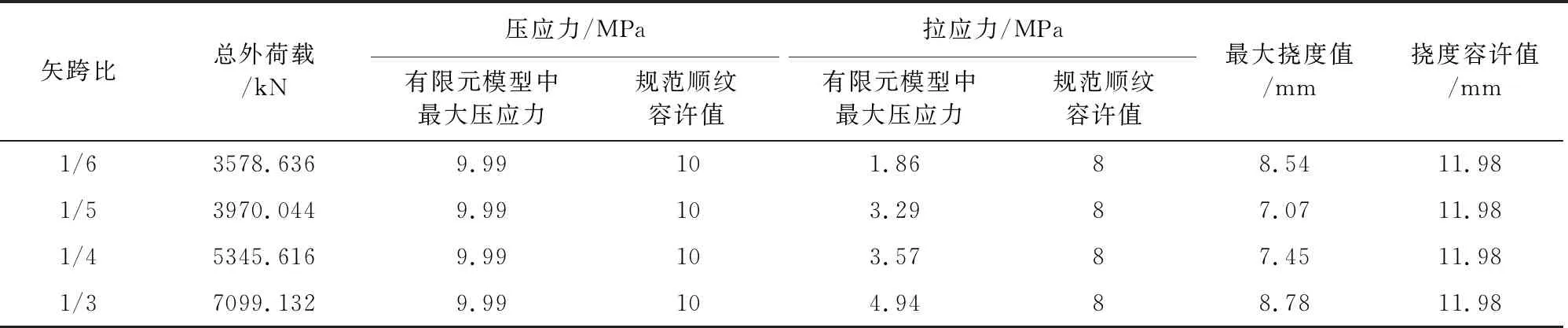
表7 极限承载能力状态下拱肋最大应力、挠度及外荷载
综合上述强度分析、挠度分析和极限承载能力分析可知:在承载能力极限组合作用下,随着拱肋结构矢跨比的增大,拱肋节点处的角度随之减小,拱肋最大应力值和最大挠度值均逐渐递减;当拱肋结构达到极限承载能力时,随着矢跨比的增大,拱肋结构所能承受的外荷载也随之增大。查阅桥涵设计规范,针对拱桥构造,矢跨比不宜大于1/4,故我们采用1/4矢跨比作为最优矢跨比。
2.3 节间数分析
2.3.1 强度分析
在承载能力极限组合作用下,不同节间数所对应的拱肋最大应力值见表8。
不同矢跨比所对应的拱肋应力图如图11、图12、图13所示,不同矢跨比所对应的拱肋最大应力值的变化图如图14所示。

表8 不同节间数所对应的拱肋最大应力值

图11 五节拱对应的拱肋应力图

图12七节拱对应的拱肋应力图

图13九节拱对应的拱肋应力图
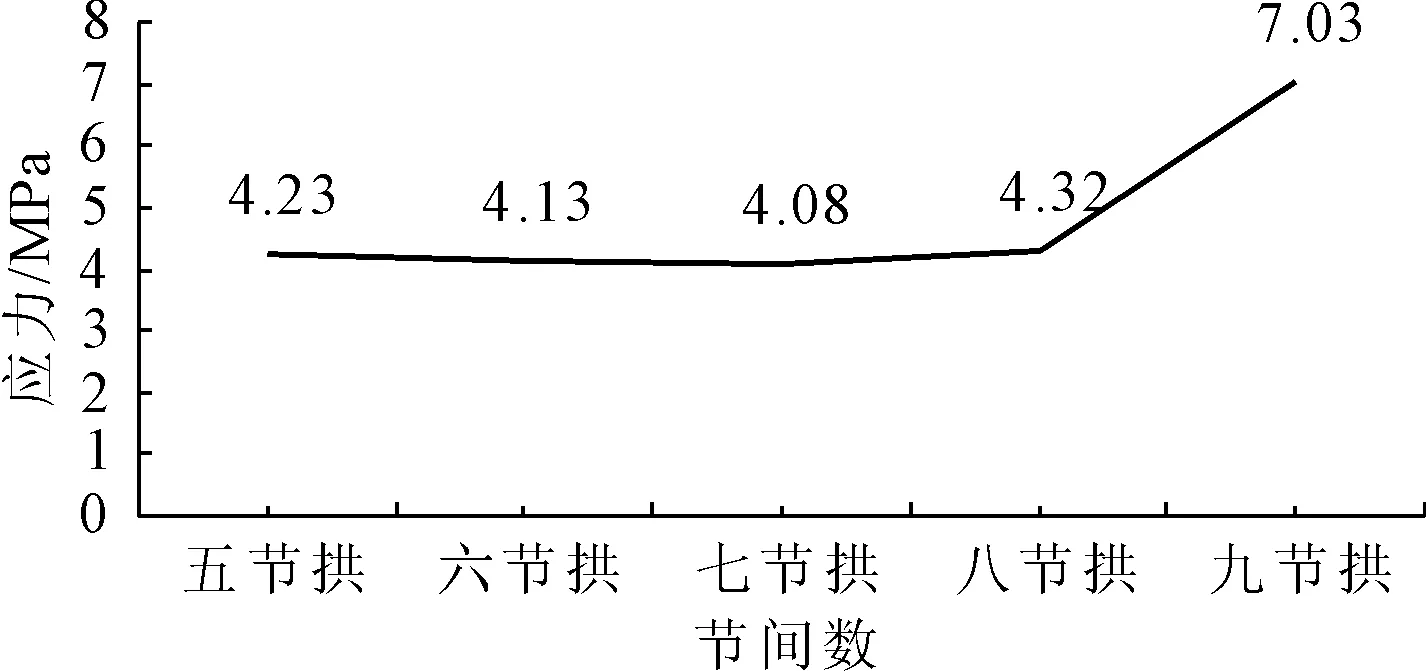
图14不同节间数对应的拱肋结构最大应力变化图
由上述计算结果,可以看出:随着节间数的增加,拱肋结构内最大应力先减小然后突然增大。
(1) 由于节点对整体结构的强度存在削弱作用[13],当结构为五节拱、六节拱或者七节拱时,结构节点数相对较少,节点数增加对于结构的削弱作用还不是很明显,并且,节间数的增加使结构渐渐趋近于真正的圆拱,其受力形式也与真正的拱形越来越相似,拱肋内最大压应力逐渐减小。
(2) 当结构为超过七节拱的拱形时,节点数相对较多,反而使得结构趋于复杂,且较多的节点对结构强度刚度有着明显的削弱,又由于结构已经十分接近真正的圆拱形,通过增加节间数使结构获得趋近于圆拱的受力形式已经不能抵消节点的消弱作用,反而会引起拱肋内最大压应力增大,结构受力不合理。
2.3.2 挠度分析
在承载能力极限组合作用下,不同节间数所对应的拱肋竖向挠度最大值见表9,表中竖向位移数值以竖直向下为正。
不同节间数所对应的拱肋竖向变形如图15、图16、图17所示,不同矢跨比所对应的拱肋竖向挠度最大值的变化图如图18所示。

表9 不同节间数所对应的拱肋竖向挠度最大值
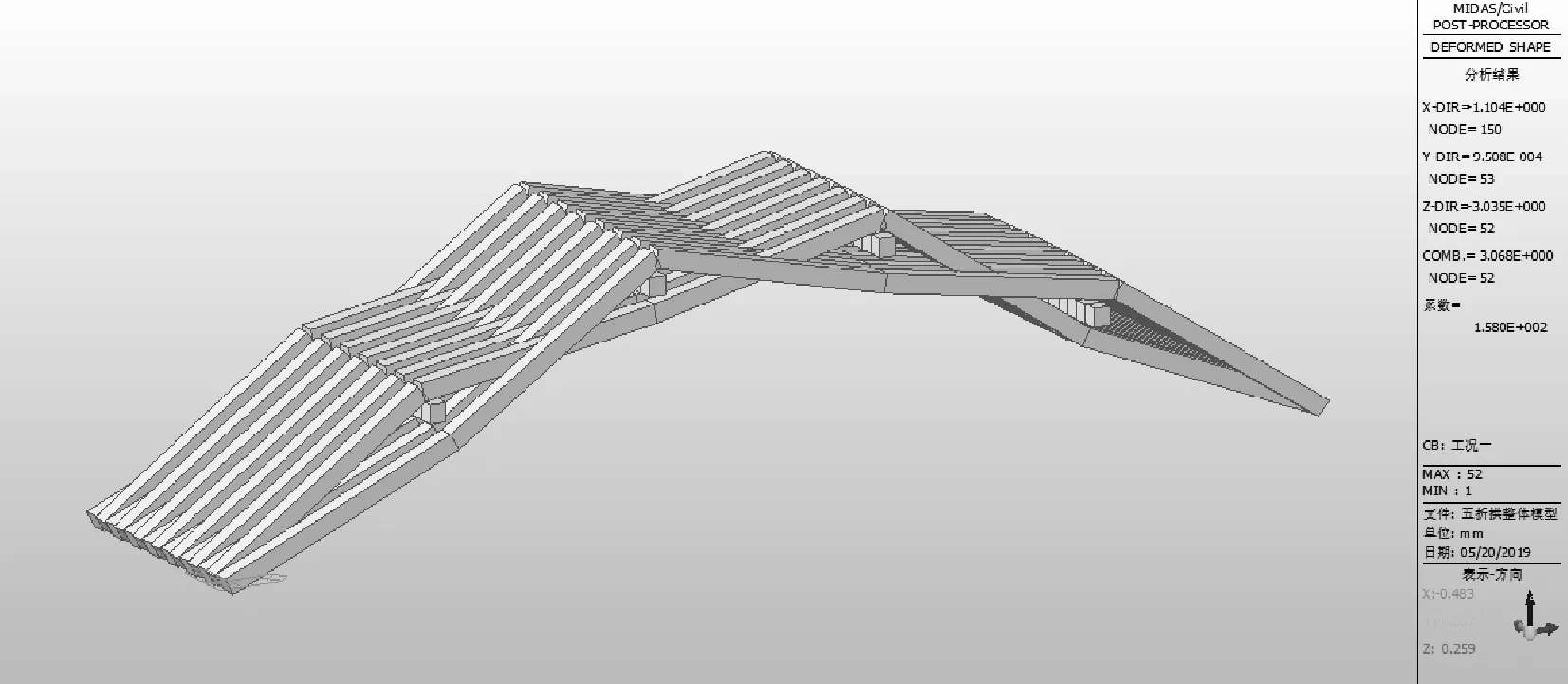
图15五节拱对应的拱肋竖向位移图

图16七节拱对应的拱肋竖向位移图

图17九节拱对应的拱肋竖向位移图
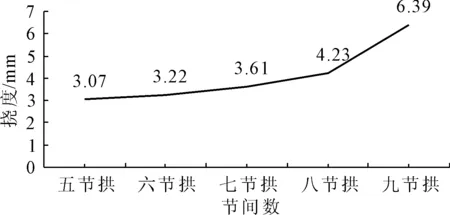
图18不同节间数对应的拱肋竖向挠度变化图
由上述计算结果,可以看出:随着节间数的增加,拱肋结构的最大挠度值一直增大。
由于节点对整体结构的刚度存在削弱作用,随着节间数的增加,结构节点也随之增多,结构的整体刚度也逐渐降低,虹桥拱肋的最大挠度也随之逐渐增大。当结构在五节拱至七节拱之间,挠度增加较为缓慢,彼此相差不大;当拱肋结构超过七节拱时,挠度增幅很大,可见结构的刚度会随节间数的增加不断减弱,也就是说,由于节点的增加,使得结构变“柔”[14]。
2.3.3 极限承载能力分析
当拱肋结构达到极限承载能力状态时,拱肋最大应力、最大挠度及施加总荷载见表10。

表10 极限承载能力状态下拱肋最大应力、挠度及外荷载
从计算结果可以看出:当拱肋结构达到极限承载能力时,随着拱肋结构节间数的增加,构件所能承受的总外荷载先增大后减小。
综合上述强度分析、挠度分析和极限承载能力分析可知:在承载能力极限组合作用下,当结构为七节拱时,拱肋内的最大压应力最小,而最大挠度与五节拱、六节拱的最大挠度相差较小;当拱肋结构达到极限承载能力时,拱肋为七节拱时,结构所能承受的外荷载最大,故七节拱是较优的结构形式。
2.4 拱肋截面分析
2.4.1 强度分析
在承载能力极限组合作用下,不同截面尺寸所对应的拱肋最大应力值见表11。

表11 不同节间数所对应的拱肋最大应力值
不同截面尺寸所对应的拱肋应力图如图19、图20、图21所示,不同截面尺寸所对应的拱肋最大应力值的变化图如图22所示。

图19截面1对应的拱肋应力图
由上述计算结果可以看出:随着截面尺寸的增加,拱肋结构内最大应力逐渐减小。
由于拱肋自重远小于节点处施加的外荷载,随着截面尺寸的增大,结构刚度也随之增大,拱肋自重增大对结构的影响远小于拱肋刚度增大对结构的影响[15]。因而在合理的截面尺寸范围内,随着拱肋截面尺寸的增大,拱肋结构越有利于受力。

图20截面3对应的拱肋应力图

图21截面4对应的拱肋应力图
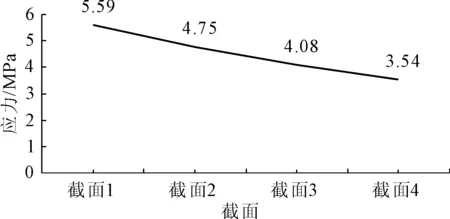
图22不同截面尺寸对应的拱肋结构最大应力变化图
2.4.2 挠度分析
在承载能力极限组合作用下,不同截面尺寸所对应的拱肋竖向挠度最大值见表12,表中竖向位移数值以竖直向下为正。
不同截面尺寸所对应的拱肋竖向变形如图23、图24、图25所示,不同截面尺寸所对应的拱肋竖向挠度最大值的变化图如图26所示。

表12 不同节间数所对应的拱肋竖向挠度最大值

图23截面1对应的拱肋竖向位移图
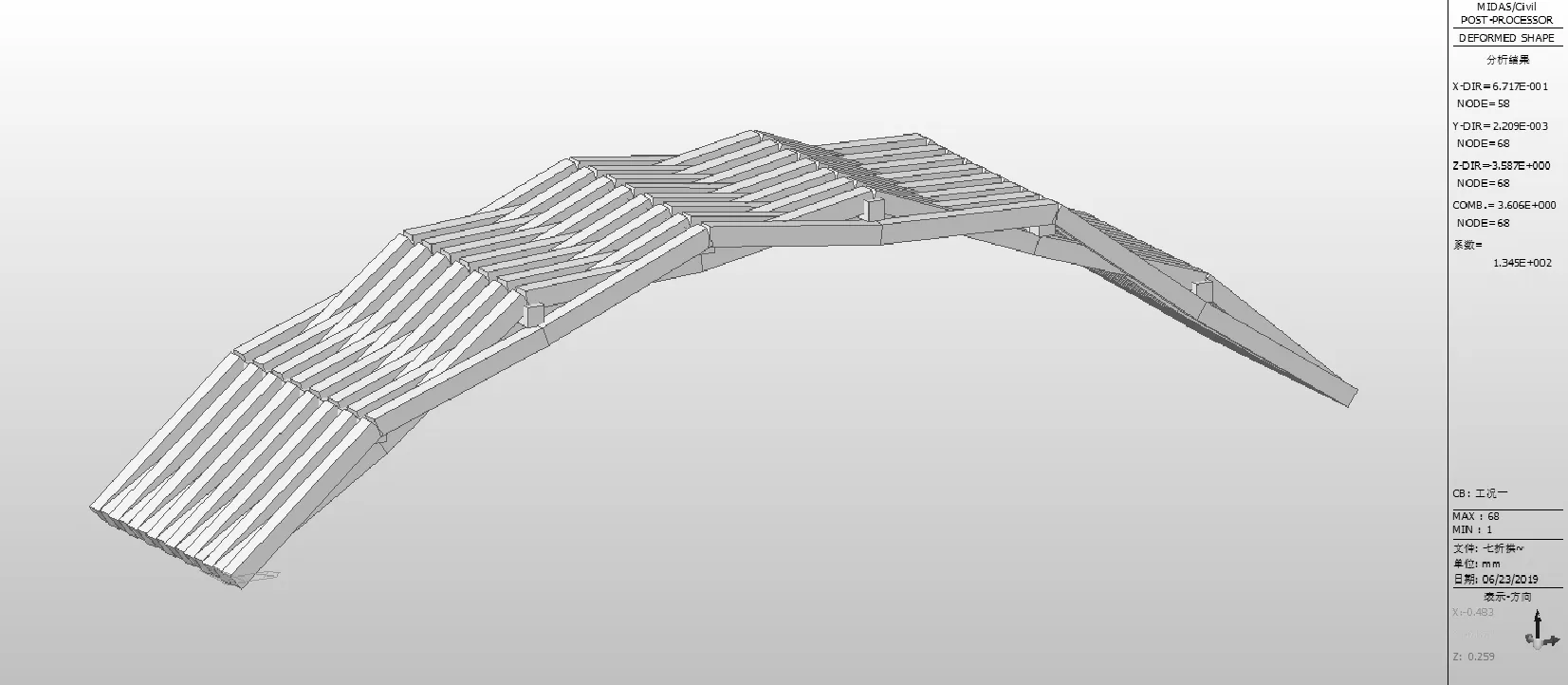
图24截面3对应的拱肋竖向位移图

图25截面4对应的拱肋竖向位移图
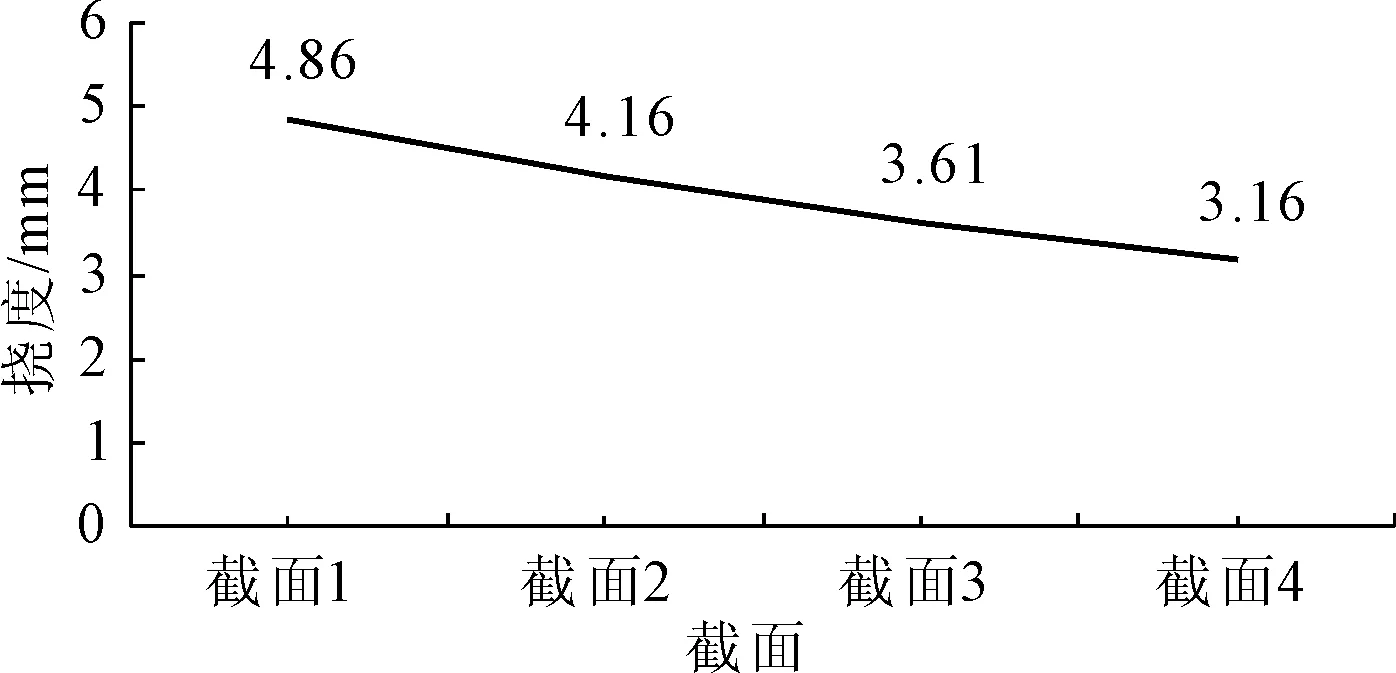
图26不同截面尺寸对应的拱肋竖向挠度变化图
由上述计算结果可以看出:随着截面尺寸的增加,拱肋结构的最大挠度随之减小。
由于拱肋自重远小于节点处施加的外荷载,随着截面尺寸的增大,结构刚度也随之增大,拱肋结构的最大竖向挠度也随之减小。
2.4.3 极限承载能力分析
当拱肋结构达到极限承载能力状态时,拱肋最大应力、最大挠度及施加总荷载见表13。
从计算结果可以看出:当拱肋结构达到极限承载能力时,随着拱肋结构截面尺寸的增加,构件刚度随之增大,结构所能承受的总外荷载也随之增大。
综合上述强度分析、挠度分析和极限承载能力分析可知:在承载能力极限组合作用下,随着拱肋截面尺寸的增大,拱肋最大应力和最大挠度逐渐减小;当拱肋结构达到极限承载能力时,随着拱肋截面尺寸的增大,拱肋所能承受的最大荷载随之增大。
3 结 论
(1) 通过上述分析可知:拱肋结构的矢跨比主要通过影响构件节点处的几何关系来影响结构的承载能力;而拱肋结构的节间数和拱肋截面尺寸主要通过影响构件的刚度来影响结构的承载能力的。
(2) 在承载能力极限组合作用下,随着矢跨比的增加,拱肋结构内的最大应力和最大挠度均随之减少:随着节间数的增加,拱肋内应力也逐渐减少,但当结构拱形超过七节拱时,随着节间数的增加,节点也随之增多,趋近于圆拱的受力形式已经不足以抵消大量节点带来对的结构的削弱作用了,使得拱肋内应力不减反增;随着拱肋截面的增大,拱肋结构内的最大应力和最大挠度均随之减少。
(3) 当拱肋结构达到极限承载能力时,随着矢跨比的增大,拱肋结构所能承受的外荷载也随之增大;随着拱肋结构节间数的增加,构件所能承受的总外荷载先增大后减小;随着拱肋截面尺寸的增大,拱肋所能承受的最大荷载随之增大。
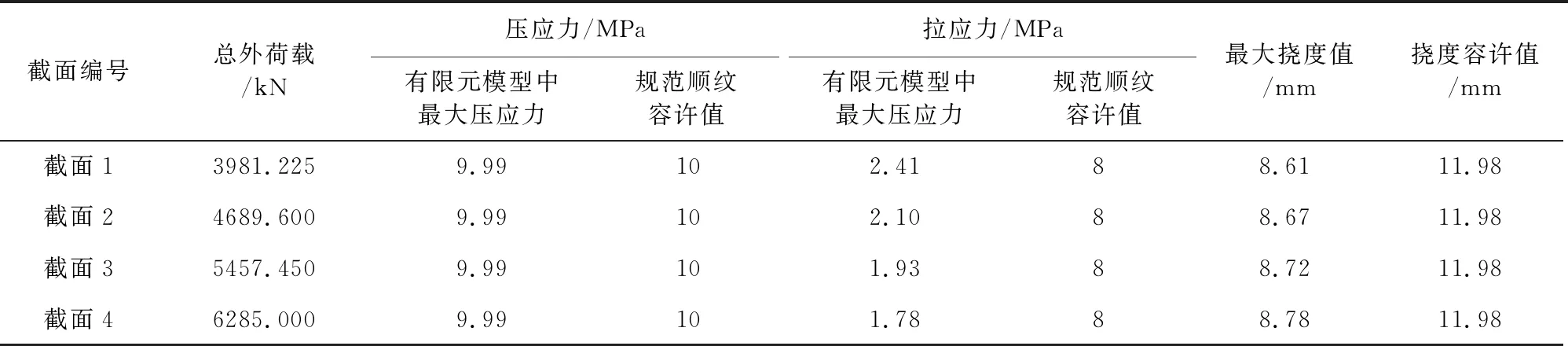
表13 极限承载能力状态下拱肋最大应力、挠度及外荷载
(4) 通过对改变拱肋结构矢跨比、节间数和拱肋截面尺寸的分析比较中发现,在设计类似木拱桥时,要根据现场实际情况充分考虑上述三个因素对编木拱结构的影响,以得到一个最为合理的矢跨比、节间数和拱肋截面尺寸。
