集值优化问题E-全局真有效解的非线性标量化定理
2019-11-04仇秋生潘铭敏
仇秋生, 潘铭敏
(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)
0 引 言
标量化方法就是将集值优化问题转化为数值优化问题,建立集值优化问题的解与数值优化问题最优解之间的联系.由于数值优化问题的理论与算法相对比较成熟,所以,通过标量化,集值优化问题的解可由求解数值优化问题得到.同时,标量化方法还是研究集值优化问题解集性质的有力工具.标量化方法主要有线性标量化和非线性标量化.而线性标量化通常借助凸集分离定理、择一性定理等得到各种解的标量刻画,对目标函数及可行集有一定的凸性要求.然而,在实际生活中,许多集值优化问题是非凸的,因此,非线性标量化方法日益成为研究的热点.文献[1]在凸锥内部非空的情况下,借助Minkowski泛函构造了非线性标量化函数,人们称之为Gerstewitz泛函,这一泛函也被称为最小严格单调函数.Gerstewitz泛函被广泛应用于可行集不是凸集的向量优化和向量均衡问题.随后,文献[2]在拓扑线性空间中运用非凸分离定理,对向量优化问题的弱有效解和真有效解进行标量刻画;文献[3]在赋范线性空间中利用连续的最小严格单调泛函,给出了Henig真有效点的非线性标量化定理;文献[4]在拓扑线性空间中引入了基于改进集的非线性标量泛函,讨论了向量优化问题的E-弱有效解和E-Benson真有效解的标量化定理;文献[5]将Gerstewitz泛函的主要性质从拓扑线性空间推广到一般的实线性空间,讨论了Gerstewitz泛函的正齐性和单调性等,并给出了向量均衡问题弱有效解的非线性标量化定理;文献[6]在一般的线性空间中建立了基于序锥的拟相对内部的非凸分离定理.
在不具备拓扑结构的线性空间中,对集值优化问题统一解的非线性标量刻画的研究比较少.因此,在文献[7-11]的基础上,本文在实线性空间中引入基于改进集的非线性标量泛函,利用集合代数内部和向量闭集的性质,得到了非凸分离定理,对集值优化问题的E-弱有效解和E-全局真有效解进行标量化刻画,去掉了目标函数及可行集的凸性要求.
1 预备知识
若无特别申明,以下总设X,Y是实序线性空间.0表示每个空间的零元.记R+=[0,+∞),R++=(0,+∞).设K是Y的非空子集,若∀k∈K,λ≥0,有λk∈K,则称K为锥;若锥K还是凸集,则称K为凸锥;若锥K满足K∩(-K)={0},则称K为点锥.锥K是非平凡的当且仅当K≠{0}且K≠Y.
以下均假设K为非平凡的凸锥.
定义1[11]设E是Y中的非空子集,若0∉E且E+K=E,则称E是关于锥K的改进集,简称E是改进集,记Y中所有改进集的集合为ζY.
定义2[12]若M是Y中的非空子集,则称
corM:={m∈M| ∀y∈Y,∃λ′>0,∀λ∈[0,λ′],m+λy∈M},
vclM:={m∈Y| ∃y∈Y,∀λ′>0,∃λ∈(0,λ′],m+λy∈M}
分别为M的代数内部和向量闭集.
引理1设K是Y中的凸锥且corK≠Ø,对∀q∈corK,有Y=qR++-K.
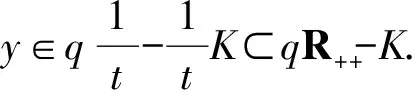
引理2[13]设K是Y中代数内部非空的凸锥,若E∈ζY,则corE=E+corK.
引理3[12]若M⊂Y是非空子集,K是代数内部非空的凸锥,则
1)cor(M+K)=cor(vcl(M+K));
2)cor(vcl(M+K))=M+corK.
命题1设K⊂Y是代数内部非空的凸锥,E⊂Y是关于锥K的改进集,则corE= vclE+corK.
证明 由于E+corK⊂vclE+corK,而corE=E+corK,所以
corE⊂vclE+corK.
另一方面,
vclE+corK⊂cor(vclE+K).
(1)
下证vclE+K⊂vcl(E+K). 对∀y∈vclE+K,∃e∈vclE,k∈K,使得y=e+k.由于e∈vclE,所以∃b∈Y,∀ε>0,∃t∈[0,ε],有e+tb∈E.因此,
y+tb=e+k+tb∈E+K.
由向量闭集定义知y∈vcl(E+K).所以,vclE+K⊂vcl(E+K).则由式(1)和引理3的1)知,
vclE+corK⊂cor(vcl(E+K)) =cor(E+K)=corE.
因此,vclE+corK⊂corE.综上,corE=vclE+corK.命题1证毕.
注1若E不是关于K的改进集,则命题1不一定成立.

设W⊂X是非空子集,F:W→2Y是集值映射,考虑如下集值优化问题:



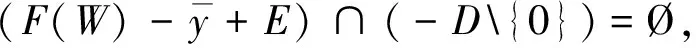

注2线性空间中基于改进集的全局真有效性是一个一般性的概念,它包括全局真有效性和近似全局真有效性等作为特殊情况.
2 实线性空间中基于改进集的非线性标量化泛函
Gerth等[2]在拓扑线性空间中提出了一类最小严格单调函数,也被称为Gerstewitz 泛函,在非凸优化问题中有着广泛的应用.
下面在实线性空间中引入基于改进集的非线性标量化泛函.
命题2设Y是线性空间,K⊂Y是代数内部非空的凸锥,E⊂Y是关于K的改进集,q∈corK,令Q(y)={t∈R|y∈tq-E},则集合Q(y)是下有界的.
证明 由于Q(y)={t∈R|y∈tq-E},因此,若t1∈Q(y),则t1∈R,且y∈t1q-E.当λ>t1时,
y-λq=y-t1q+(t1-λ)q∈-E-corK=-corE⊂-E,
这说明λ∈Q(y),即
若t1∈Q(y),λ>t1,则y∈λq-E.
(2)
下证Q(y)≠R.假设Q(y)=R,则对∀λ∈R,有y∈λq-E.对∀z∈Y,有-z∈Y.由引理1知,∃k′∈K和s>0,使得-z=sq-k′.因为Q(y)=R,所以-s∈Q(y),即y+sq∈-E.因此,
-z=sq-k′+y-y=(y+sq)-k′-y∈-E-K-y=-E-y.
由z的任意性知,-Y⊂-E-y,因此Y=E,与E是改进集矛盾.故假设不成立,从而Q(y)≠R.
由式(2)知,若t1∉Q(y),则当μ 定义5设K⊂Y是代数内部非空的凸锥,E⊂Y是关于K的改进集,q∈corK,定义如下的泛函: ξq,E(y)=inf{t∈R|y∈tq-E}, ∀y∈Y. 规定inf Ø=+∞. 注3ξq,E(y)关于序锥K是不减的,这是因为,对∀y1,y2∈Y,y2-y1∈K.若ξq,E(y2)=∞,则ξq,E(y1)≤ξq,E(y2).若ξq,E(y2)<∞,则对任意满足y2∈tq-E的t有 y1∈y2-K⊂tq-E-K=tq-E. 因此,ξq,E(y1)≤t,进而ξq,E(y1)≤ξq,E(y2).综上,ξq,E(y)关于K是不减的. 由向量闭集和集合代数内部的性质获得基于改进集的非线性标量化泛函的下列重要性质: 定理1设Y是实线性空间,E⊂Y是关于K的改进集,q∈corK,则 1){y∈Y|ξq,E(y)<λ}=λq-corE; 2){y∈Y|ξq,E(y)≤λ}=λq-vclE. 证明 1)首先证明{y∈Y|ξq,E(y)<λ}⊂λq-corE.∀y′∈{y∈Y|ξq,E(y)<λ},存在s<λ,使得y′∈sq-E.已知q∈corK,则 y′∈λq-((λ-s)q+E)⊂λq-((0,∞)q+E)⊂λq-(corK+E)=λq-corE, 即y′∈λq-corE.因此,{y∈Y|ξq,E(y)<λ}⊂λq-corE. 下证λq-corE⊂{y∈Y|ξq,E(y)<λ}.对∀z∈λq-corE,有λq-z∈corE.因为q∈corK⊂Y,所以-q∈Y.又因为λq-z∈corE,所以对于-q∈Y,存在α>0,使得λq-z-αq∈E,即z∈(λ-α)q-E.因此,ξq,E(z)≤λ-α<λ. 下证{y∈Y|ξq,E(y)≤λ}⊂λq-vclE.对∀u∈{y∈Y|ξq,E(y)≤λ},当ξq,E(u)<λ时,由定理1的1)可知, u∈λq-corE⊂λq-vclE. 结论显然成立. u∈tnq-E. (3) 下面分2种情况讨论: ①若存在n0,使得tn0=λ,则由式(3)知,u∈tn0q-E=λq-E⊂λq-vclE.结论得证. λq-u+αnq∈E. 所以,λq-u∈vclE,即u∈λq-vclE.因此,{y∈Y|ξq,E(y)≤λ}⊂λq-vclE.定理1证毕. 下面对集值优化问题基于改进集的弱有效解和全局真有效解进行标量刻画. 考虑由集值优化(VP)诱导的标量化问题: 其中:y∈Y;q∈corK;E∈ζY;ξq,E由定义5所定义. 下面讨论实线性空间中集值优化问题E-弱有效解和E-全局真有效解的非线性标量化定理. (4) 由定理1知,当λ=0时,{y∈Y|ξq,E(y)<0}=-corE.因此,由式(4)得 这表明 (5) ξq,E(0)=inf{t∈R|0∈tq-E}=inf{t∈R|tq∈E}≤inf{t∈R+|tq∈E}=ε, 所以 (6) 然而,存在y′=(-1,-1),使得 (7) ξq,E(0)≥0. (8) 假设ξq,E(0)<0,则存在t1<0,使得0∈t1q-E,即t1q∈E.由于q∈corK⊂K,所以-t1q∈K.因此, 0=t1q-t1q∈E+K=E. 这与E是改进集矛盾,故假设不成立.因此,ξq,E(0)≥0.从而 ξq,E(0)=inf{t∈R|tq∈E}=inf{t∈R+|tq∈E}=ε. (9) 注5对于ξq,E(0),我们无法得到ξq,E(0)>0这一结论,因为ξq,E(0)=0的情况仍有可能出现. 显然, (10) 与式(10)矛盾,因此假设不成立,即 (11) 由定理1知,当λ=0时,{y∈Y|ξq,E(y)<0}=-corE.因此,由式(11)得 这表明 (12) ξq,E(0)=inf{t∈R|tq∈E}≤inf{t∈R+|tq∈E}=ε. 因此, (13) 注6定理4的逆命题不一定成立. 又由于 为了对不具备拓扑结构的非凸集值优化问题进行标量刻画,引入了实线性空间中基于改进集和集合代数内部的非凸分离定理,克服了线性标量化定理中对集值优化问题目标函数和可行集的凸性要求.作为应用,给出了线性空间中集值优化问题E-全局真有效解和E-弱有效解的非线性标量化定理.由于集值优化问题的E-有效性具有统一性和一般性,因此,本文提出的基于改进集的非凸分离定理对精确和近似的真有效解都成立.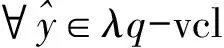

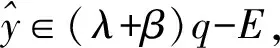
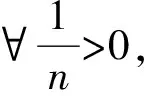

3 E-全局真有效解的非线性标量化定理

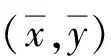
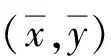
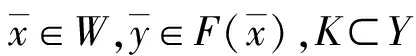
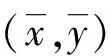
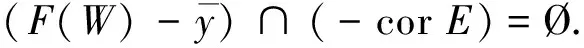

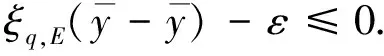
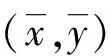
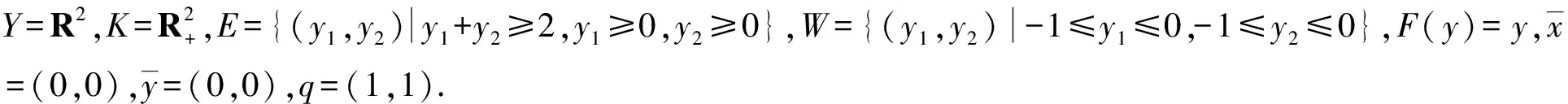
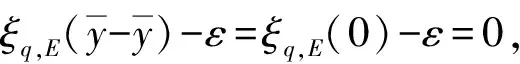
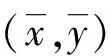
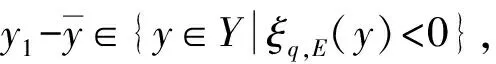

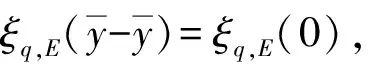
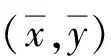
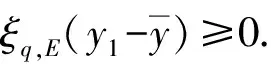
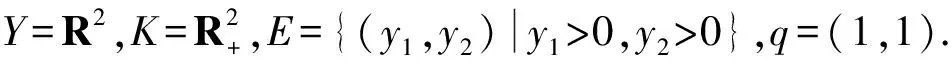

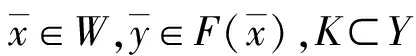
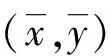

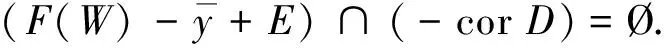
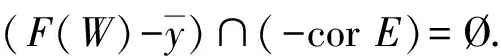
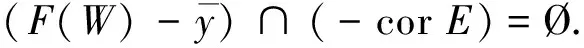

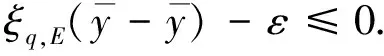
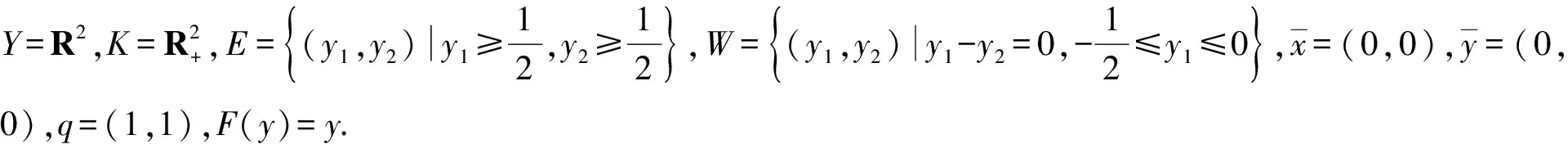

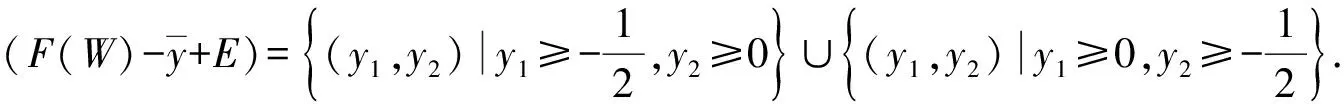
4 结 语
