基于深度自编码器的大型龙门加工中心热误差建模方法
2019-11-04杜柳青王承辉余永维
杜柳青 王承辉 余永维 徐 李
(重庆理工大学机械工程学院, 重庆 400054)
0 引言
热误差具有时变、非线性和耦合的特点,不同的工况会导致机床不同的温度分布模式和不同的热误差。传统方法如核主成分分析、多尺度变换法等只适合服从高斯分布和服从线性分布的特定数据集,且在提取特征时需依靠现场经验和专业知识,限制了特征集的表达;为提高模型的精确度,常在机床关键位置布置大量温度传感器,导致相邻测点的输出信号具有较大的多重相关性[3]。因此,热误差预测是一个高维、大样本问题。高维数据会产生维数灾难,会造成建模的拟合效果良好、而预测效果差的现象;同时传统方法建立的模型会因环境和季节的变化而表现出很强的阶段性效应,尤其是在样本量较少的情况下,难以满足热误差模型的鲁棒性要求,在一定程度上制约了热误差补偿技术的实施。
深度学习由于深度特征的挖掘能力而受到广泛关注。为解决模型的非线性、小样本和维数灾难等问题,本文将深度学习引入机床热误差建模,通过采集足够数量的样本,利用数据重构进行温度特征的提取。
1 热误差建模原理
热误差模型的原理如图1所示,首先将温度数值进行归一化处理,通过温度测点优化筛选出与主轴3个方向热误差相关性较大的测点。然后将关键温度测点的数值作为自变量输入到堆叠自编码器神经网络中,提取出温度的相应特征。最后将该温度特征作为自变量,相应的热误差作为因变量输入GA-BP神经网络训练并进行热误差预测。
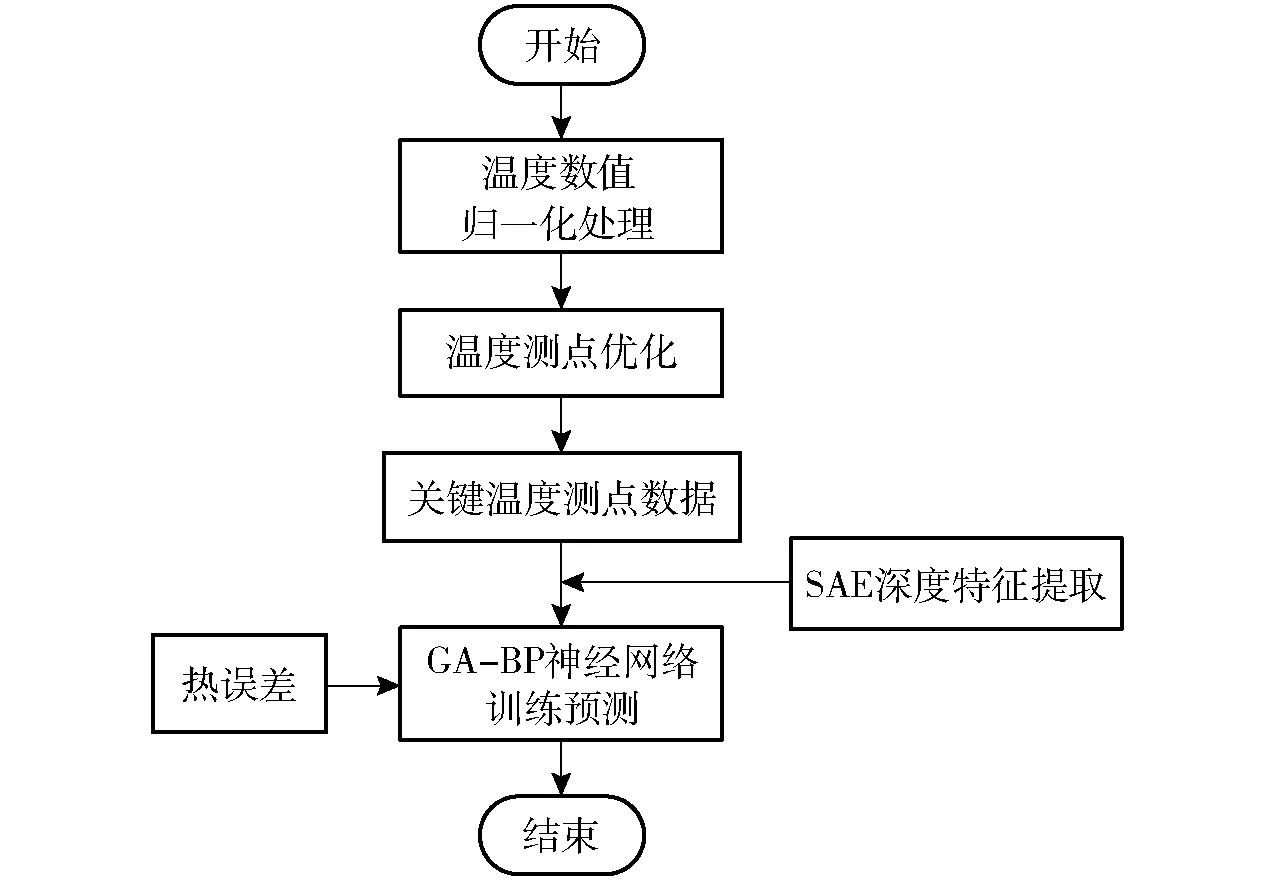
图1 热误差模型原理图Fig.1 Schematic of thermal error model
2 基于SAE的温度数据特征挖掘
2.1 自动编码器网络特征提取原理
自动编码器(Auto-encoder, AE)[10]是一种尽可能重构输入信号的3层无监督学习神经网络,利用贪婪逐层训练算法初始化网络权重,并使用BP反向传播算法微调网络参数,优化整体性能,其结构如图2所示。
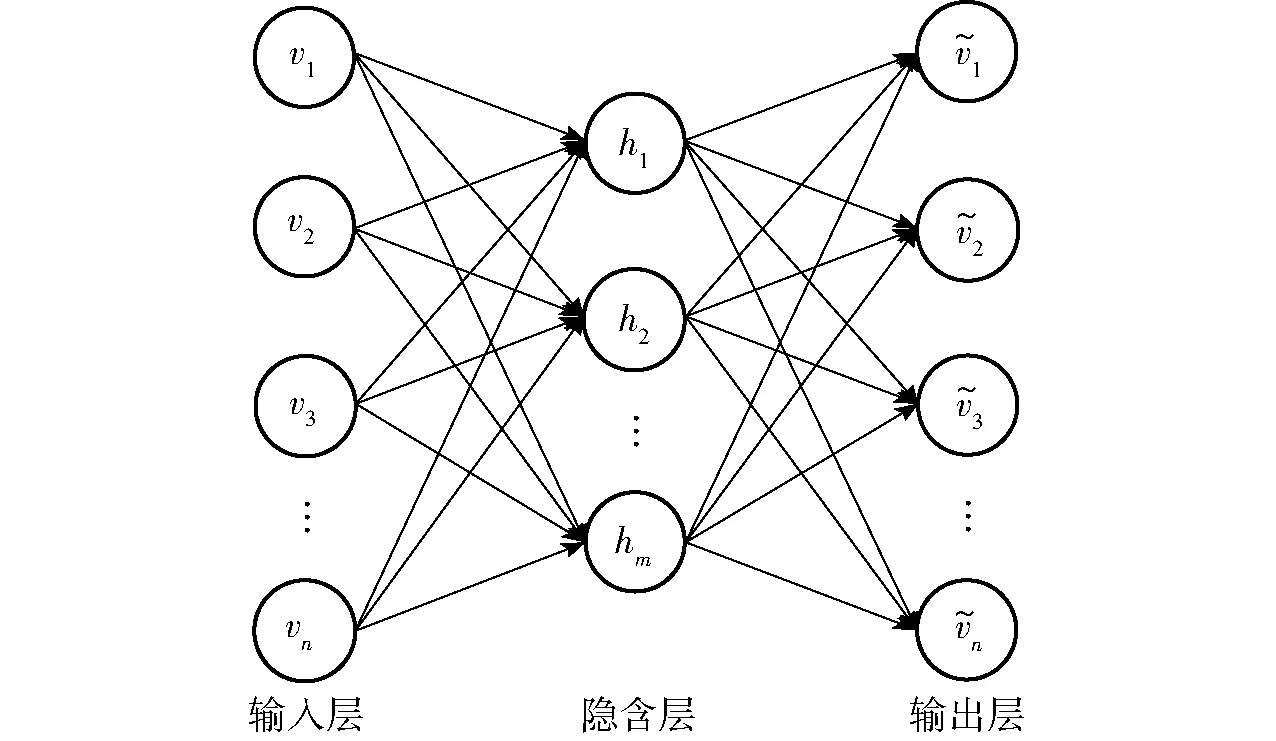
图2 自动编码器结构图Fig.2 Structure chart of auto-encoder
自动编码器的输入数据和输出目标相同,包含编码器和解码器两部分,有1个输入层、1个隐含层和1个输出层。由于输出层可对输入数据进行重构,因此编码矢量称为输入数据的一种特征表示[11]。
假设输入样本集v=(v1,v2,…,vn),编码器定义的编码函数为fθ,解码器定义的重构函数为gθ′。先使用编码函数fθ将每个训练样本vi转换为隐含层矢量,即
(2)状态2(t0~t1):在t0时刻,开通Sa3,由于Lr限制了Sa3发生开通动作时的电流上升速度,所以Sa3在开通时处于零电流软开通状态.在该状态中,电源电压Edc施加在Lr两端,iLr以恒定的速度增大,当iLr在t1时刻增大到阈值Ia时,本状态结束.
h=fθ(v)=s(Wv+b)
(1)
式中s——sigmoid激活函数
W——输入层到隐含层的权值矩阵
b——偏置系数
(2)
式中W′——隐含层到输出层的权值矩阵
b′——偏置系数
AE算法通过网络训练寻找最优的参数矩阵,最小化输出数据与输入数据的误差。因此,需要构建误差损失函数用于网络训练,误差损失函数为
(3)
式中i——样本序号
m——样本总数量
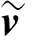
2.2 深度自编码器的网络构建及特征挖掘
深度自编码器是由多个浅层自编码器堆叠形成的深度神经网络,可以逐层地学习数据特征[12]。其网络层数越多,提取的特征也就越抽象[13]。在构建该网络模型中,SAE结构的隐含层数和节点数是自动编码器模型的重要参数。模型的输入层节点个数为4,对应的期望输出节点个数为4。分别设置不同过程的神经元隐含层节点个数和隐含层层数,比较重构误差,确定其网络结构。由表1可知,当SAE深度隐含层数增加到一定限度时,重构误差不再减小,反而增加。由表1可知,当选择节点为4-3-2-3-4的结构时,即将自编码器堆叠形成堆叠自编码器,此时数据的重构误差最小,表示输入数据已被很好地编码。
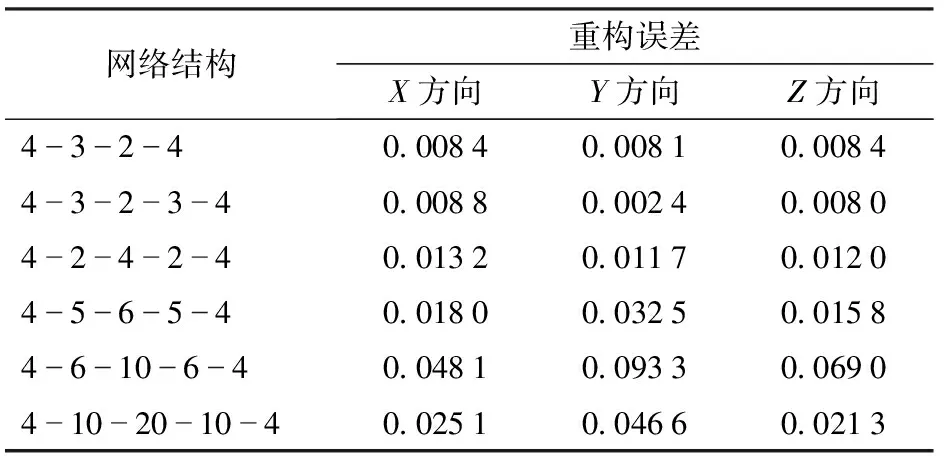
表1 不同网络结构的重构误差比较Tab.1 Comparison of reconfiguration errors for different network structures
2.3 深度自编码器网络训练及参数优化
深度学习一般包括逐层预训练和微调两个阶段。根据表1的结构,先选择所采集的数据进行预训练。在预训练阶段,每层作为一个自编码器进行训练,其目标是最小化重构误差。在每一层进行特征提取,提取的隐含层作为下一个隐含层的输入。当所有的层预训练完成时,神经网络进入微调阶段。在该阶段,对整个神经网络进行反向传播使得预测误差最小化,图3为具有4个隐含层的堆叠自编码器的结构图。其中,神经网络的学习参数设置如表2所示。堆叠自编码器的训练过程如图4所示。
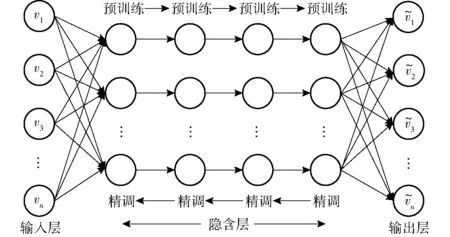
图3 具有4个隐含层的堆叠自编码器结构图Fig.3 Structure chart of stacked auto-encoders with four hidden layers

参数批量大小学习速率迭代次数稀疏标准动量值数值5029000.050.5
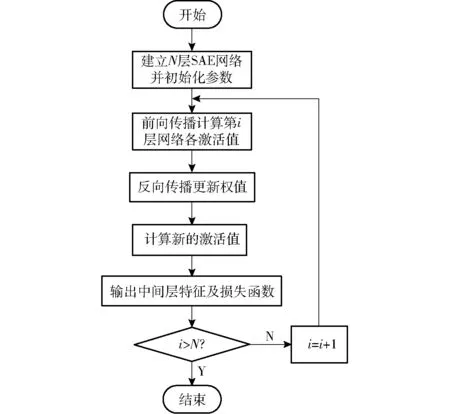
图4 堆叠自编码器网络的训练过程Fig.4 Training process of stacked auto-encoder network
3 基于GA的BP网络优化及热误差预测
BP网络是基于梯度的算法[14],存在收敛速度慢、容易陷入局部极值点和网络结构不易确定等缺点[15],而GA具有全局寻优、能自动获取搜索空间等优点[16-18],可利用GA的优点对BP网络的拓扑结构、权值、阈值和初始值进行优化,以加快 BP网络的收敛速度并提高预测精度。建模步骤如下:
(1)确定网络的输入与输出。将归一化处理后的关键点温度与主轴热误差分别作为网络的输入和输出。网络输入节点和输出节点分别设置为4和1。
(2)应用GA优化BP网络。优化BP网络的结构,确定采用3层BP神经网络作为预测模型。然后对种群的进化次数、规模、交叉概率、变异概率等进行初始化,对种群进行实数编码,并将预测输出与期望输出之间误差平方的倒数作为适应度函数;在进化搜索时,遗传算法将适应度函数作为依据,通过执行选择、交叉和变异操作计算搜索个体适应度,然后找出当前最优适应度的个体,反复迭代直至满足条件。
(3)GA-BP网络预测。当GA确定了BP网络的拓扑结构、初始值、阈值、权值后,利用样本数据对BP网络进行训练,得到最优预测模型,预测主轴热误差。通过分析结果的均方根误差和平均绝对百分比误差评价模型性能。
4 实验分析与建模
4.1 实验
主轴空运转下的热学特性(温升、热态几何精度等)是衡量机床质量的标准[19],同时为便于采集实验数据,在实验中机床处于空运转状态。实验时,机床从冷态开始运行。热机30 min后进行数据采集,并作为数据记录的时间零点,每隔5 min采集一次数据,中午暂停1 h,下午继续采集数据。实验共得到360组数据。

图5 大型龙门五面加工中心Fig.5 Large gantry five-sided machining center
如图5所示,温度和主轴热误差的采集平台为某国产龙门五面加工中心。采集所需硬件包括温度传感器、温度变送器、数据采集卡、便携式计算机和位移传感器等。其中,PT100型温度传感器具有精度高的优点,用于测量加工中心关键点的温度变化。温度通过温度传感器再经过温度变送器和数据采集卡输送到计算机中;位移传感器用于测量加工中心主轴各方向的热误差。
通过分析加工中心的热源,温度传感器布置如表3所示。
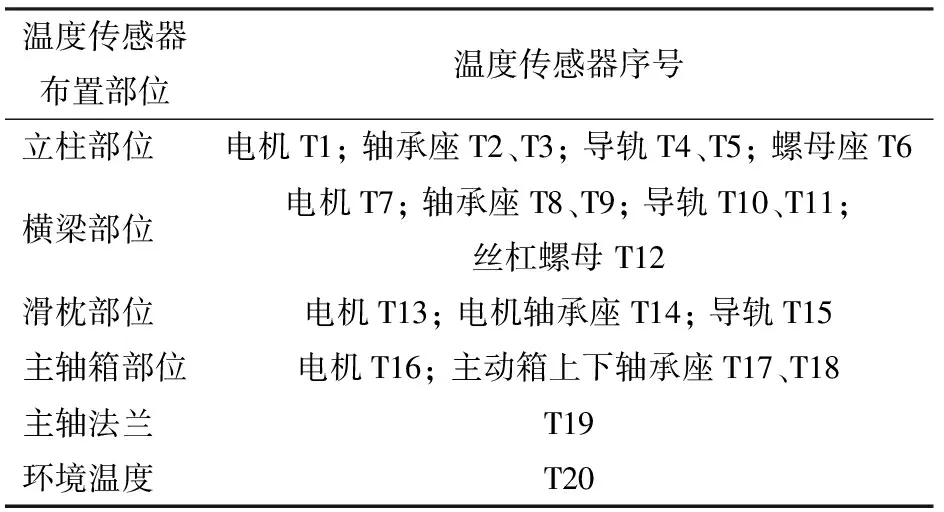
表3 加工中心温度传感器布置Tab.3 Temperature sensor arrangement of machining center
4.2 温度敏感点的选择
机床热误差由许多温度变量相互作用产生,合理地优化温度传感器测点是热误差建模中的一个重要问题,直接影响模型精度和鲁棒性。合理地选择温度测点,以最少的温度测点代替众多温度测点的同时又能较为准确地进行热误差建模是关键。通过对大型龙门五面加工中心的分析,采用模糊聚类分析[20]与灰色关联度[21]相结合的方法来选择温度关键测点,即先将各测点之间的温度数据通过聚类分析进行聚类,最后在各类测点中选取具有代表性的测点作为热误差建模所用变量。经计算,与主轴X方向具有较强相关度的温度传感器为T2、T11、T14和T18;与主轴Y方向具有较强相关度的温度传感器为T4、T5、T8和T15;与主轴Z方向具有较强相关度的温度传感器为T5、T6、T7和T12。
4.3 热误差建模
为便于建模,设计了热误差建模系统,并将本文提出的深度学习建模方法与传统的多元回归模型进行比较。模型预测结果界面如图6所示。
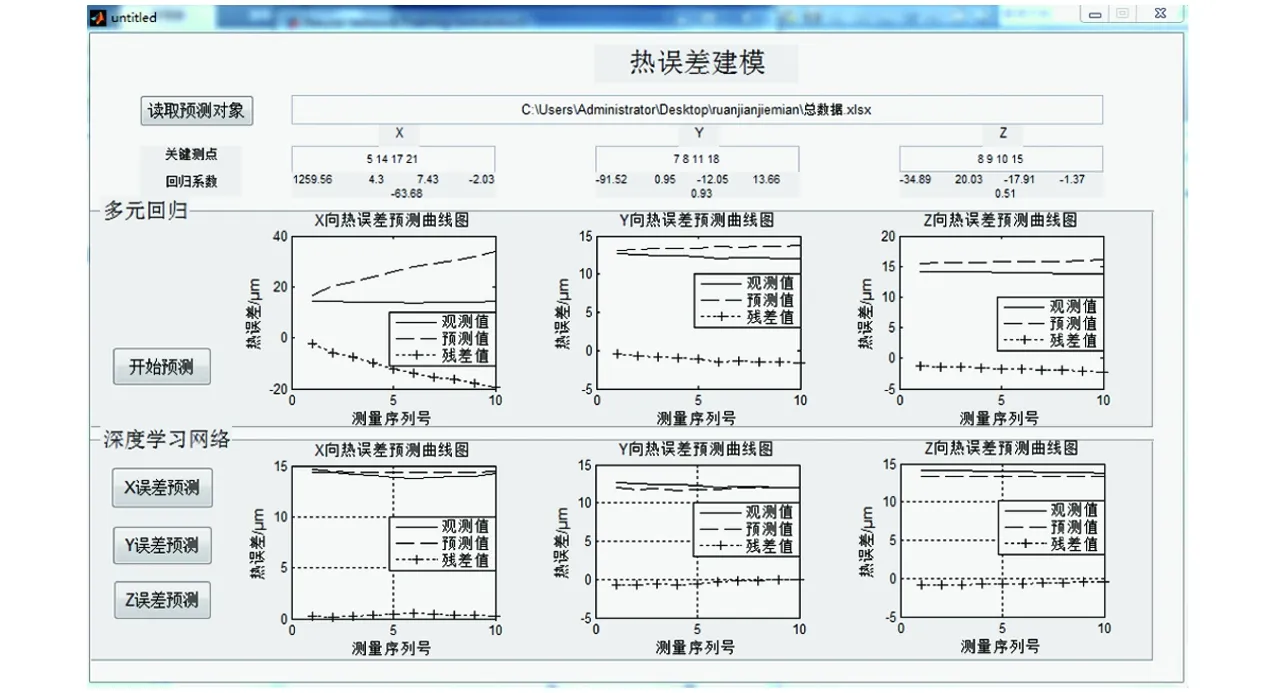
图6 热误差建模与预测界面Fig.6 Interface of thermal error modeling and prediction
首先读取预测文件,数据文件的前3列分别为X、Y、Z方向的热误差数据,从第4列起为所测得的温度,然后根据之前筛选得到的关键测点进行热误差预测。
4.4 模型精度分析
图7、8为两种模型分别在X、Y、Z3个方向上的预测曲线。实验结果表明,所提出的建模方法有较高的预测精度,优于传统多元回归模型等方法。实验时,多元回归模型的最大误差可达20 μm,深度学习模型的预测误差范围在1 μm以内。采用均方根误差(Root mean square error, RMSE)和平均绝对百分比误差(Mean absolute percentage error, MAPE)对模型的预测准确度进行评价,评价结果如表4所示。
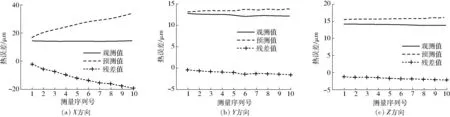
图7 多元回归模型的热误差预测曲线Fig.7 Thermal error prediction curves of multivariate regression model

图8 深度学习模型的热误差预测曲线Fig.8 Thermal error prediction curves of deep learning model
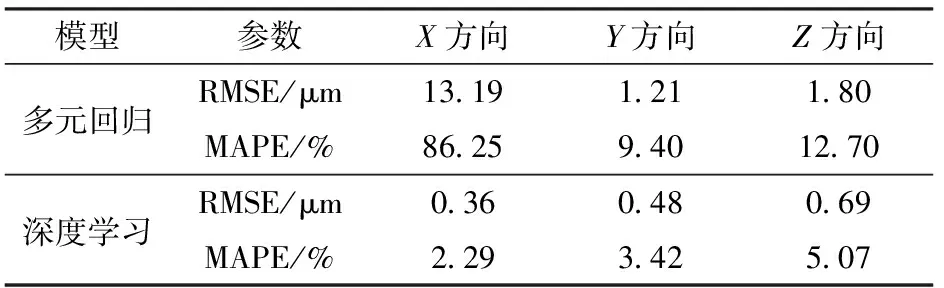
表4 预测结果评价Tab.4 Evaluation of prediction results
多元回归方法虽然计算量小,便于实现,但不能反映热误差的非线性特征,预测精度低。从图7、8及表4可看出,基于SAE-GA-BP的热误差模型与实际测得的热误差吻合情况较好,由此可见,该方法预测精度高,能够有效估计机床的热误差变化趋势。
综上所述,基于SAE-GA-BP的热误差模型的整体预测精度比传统的多元回归模型具有明显的优势,能有效弥补现有模型的局限性。
5 结论
(1)基于SAE-GA-BP的热误差建模方法可以应用于数控机床热误差建模和预测。
(2)通过对输入变量的特征提取和GA-BP神经网络算法选择最优参数后建立的模型对加工中心主轴热误差的预测值与实际值吻合程度较高,该方法预测精度高,与多元回归模型相比,更适合用于数控机床热误差建模。
