不同PDF模型在超燃冲压发动机数值模拟中的应用
2019-11-04丁海昕钟诚文
丁海昕,钟诚文
(1.西北工业大学 航空学院,西安 710072) (2.中国空气动力研究与发展中心,绵阳 621000)
0 引 言
超燃冲压发动机是未来吸气式高超声速飞行器主要动力之一,而超声速湍流燃烧,是超燃冲压发动机研究过程中的关键问题之一,也是一个突出的技术难点。燃料以各种方式喷射入燃烧室内,与超声速空气来流掺混、点火、燃烧,从而释放化学能。在此过程中,燃料在燃烧室内的驻留时间很短(一般在毫秒量级),往往伴有局部熄火等复杂的化学反应过程,给数值模拟研究带来了巨大的挑战[1]。
早期超声速燃烧的相关计算基本上只采用有限速率化学反应动力学机理,忽略了湍流与燃烧的相互作用[2]。而一些实验数据表明,在超声速燃烧室组分浓度和温度脉动可分别达到40%和20%,因此忽略这些脉动对平均反应速率的影响会导致对流场的错误描述,进而可能错误地预测流场中的主要组分分布,甚至湍流燃烧相互作用可能会影响一些设计参数,例如燃料的加注方式、火焰稳定、点火延迟、燃烧效率等,因此应该采用湍流燃烧模型来模拟超声速湍流燃烧。目前,应用于超声速湍流燃烧比较有代表性的湍流燃烧模型有概率密度函数(Probability Density Function,简称PDF)方法和火焰面模型(Flamelet Model)。
从低速流中发展起来的火焰面模型,在超声速燃烧中的存在性与适用性问题还有待进一步研究。而PDF方法是被认为解决有限反应速率和污染物生成等诸类湍流燃烧问题的最理想的方法,但概率密度函数求解的复杂性和计算量之大给其在工程中的广泛应用带来了很大的困难,因此通常采用计算量较小的简化PDF方法。
近年来,设定型PDF模型被用于超燃冲压发动机的计算中。R.A.Baurle等[3]用设定PDF模型对氢的超声速燃烧进行了模拟,结果显示基于有限速率反应的PDF模型能够较为准确描述湍流与反应之间的相互作用;M.Kindler等[4]用基于有限速率化学反应的多元设定型PDF模型计算了Hyshot超燃发动机,结果表明,考虑脉动的温度和组分PDF方法对Hyshot燃烧过程影响很大,设定型PDF模型的封闭模拟能够预测点火延迟;汪洪波等[5]采用设定型PDF模型与LES相结合以封闭亚格子湍流-燃烧相互作用,并将模型用于支板喷射超声速湍流燃烧流场的数值模拟;Pei Xinyan等[6]用PDF模型对固态燃料超燃冲压发动机进行了模拟,准确描述了凹槽结构燃烧室的激波与燃烧室相互作用;张宏达等[7]采用假定PDF模型和大涡模拟方法研究了值班预混射流火焰,假定反应变量满足β分布,能够较好的预测PPJB火焰的温度和组分质量分数的分布;赵国焱等[8]研究了基于不同PDF的混合分数概率密度函数对湍流扩散燃烧的影响,总体上混合分数β分布计算结果更好。上述研究表明,设定型PDF方法在复杂超声速燃烧流场的模拟中具有很好的应用前景,并且不同分布的预先假定PDF模型得到的结果差异较大,有必要进行深入研究。
为研究不同设定型PDF模型对超燃冲压发动机计算结果的影响,本文对NASA Langley公开发布的超燃直连式发动机模型(Hypersonic Internation Flight Research Experimentation Flight2,简称HF2)进行验证计算。
HF2采用的发动机模型来自美国空军研究实验室(AFRL),在NASA Langley研究中心的电弧加热风洞开展了直连式风洞试验。国内外已有一些学者对该模型发动机进了数值研究,分别采用CFD++、VULCAN和AHL3D等软件进行了计算[9-10],并取得了与实验相符较好的结果。然而这些数值研究要么采用RANS方法忽略湍流对化学反应的影响,要么采用涡耗散(EDC)模型来考虑湍流与化学反应的相互作用。在高雷诺数超声速燃烧中,湍流与燃烧存在强烈的相互作用,直接忽略湍流对燃烧的影响显然是不恰当的。本文采用的PDF方法用概率密度函数来考虑湍流效应,具有更广的适用性,因而在复杂超声速燃烧流场的模拟中具有很好的应用前景。
1 计算模型和方法
1.1 几何模型和网格
HF2的隔离段/燃烧室流道图如图1所示,包括一个等截面的隔离段、两个对称的开式凹槽、8个喷嘴(分别为P1和S1)和渐扩的燃烧室。几何模型在流线方向上的二维截面图如图2所示,几何模型关于z=0面和y=0面对称。燃料从P1和S1两列喷嘴中喷出,在燃烧室中采用火花塞进行点火。P1喷嘴和S1喷嘴在上下壁面各有4个,P1喷嘴直径为0.317 5 cm,位于燃烧室突扩段的上游,以15°角度斜喷入燃烧室;S1喷嘴直径为0.238 8 cm,位于燃烧室收缩段的下游,以90°垂直喷入燃烧室。隔离段横截面高为2.54 cm,宽为10.16 cm,总的长度为71.12 cm。
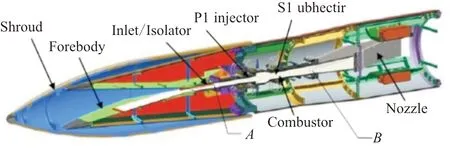
图1 HIFiRE模型示意图Fig.1 Schematic of HIFiRE model
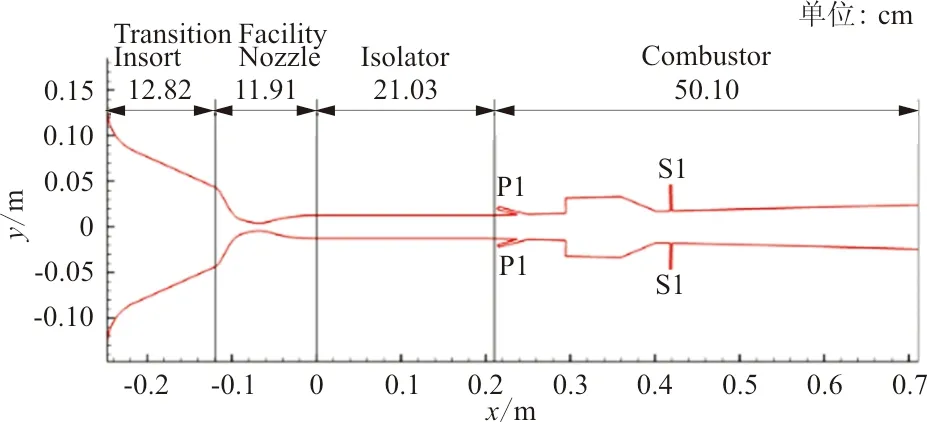
图2 HIFiRE直连式发动机对称面示意图Fig.2 Schematic of HIFiRE symmetry plane
由于发动机模型上下、左右对称,为节省计算量,根据Liu Jiwen等[11]的计算经验,采用1/4大小的模型进行计算,中间截面采用对称边界。计算网格分为56个块,网格数共计350万个。网格在壁面附近进行了指数加密,壁面第一层网格大约为0.05 mm,对应的第一层网格高度y+大约为20。
1.2 设定型PDF模型
设定型PDF模型是输运变量脉动的概率密度函数的具体形式,通过确定其中的一些待定参数来获得输运变量脉动的概率分布。输运变量脉动的概率密度函数通常采用双δ函数分布和β函数分布等形式。
(1) 双δ函数分布
(1)
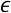
δ函数分布形式简单,待定参数容易确定,引入计算量小等性质,应用广泛。但在有些情况下,却不能给出合理的结果。
(2)β函数分布
(2)

β函数的分布形式会随参数而变化,适应性较好,但数值积分困难。
本文采用的PDF模型考虑温度脉动或组分脉动对湍流燃烧的影响,用这两个标量来描述燃烧系统的化学热力学状态参数,建立温度和组分的输运方程并假定它们脉动的概率密度函数,然后再通过概率积分确定湍流燃烧过程中所有标量的时均特性。温度和组分分数联合概率密度函数如下:
(3)
式中:P(T)为考虑温度脉动的PDF模型;P(fi)为组分脉动的PDF模型,其积分表达式为
(4)
遵循质量作用定律,积分后有:
(5)
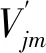
式中各项的求解方法为:
(6)
②温度的脉动T″由能量方差和输运方程的解得到,而泰勒展开中T″的高阶项由δ分布或β分布方法来计算得到。
当P(T)为δ分布时,如式(7)所示。
(7)
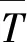
当P(T)为β分布时,要求变量范围必须介于0~1之间,因此需要将温度变量进行转换为新的变量φ,以此满足应用需求,P(T)函数表达式为
(8)
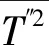
③平均正向组分生成率Ifi和逆向组分生成率Ibi由组分浓度的不同分布PDF函数进行封闭。
在湍流燃烧化学反应过程中,组分i的质量分数f和组分浓度C的关系为
(9)
式中:M为摩尔质量;ρ为密度。
式(9)也可以从化学反应进行的方向表达如下:
(10)
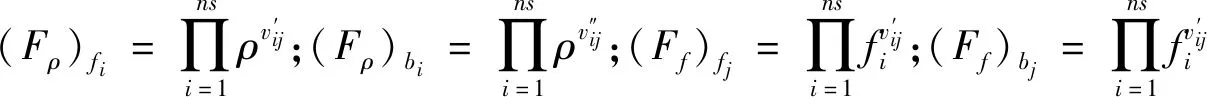
为了简化问题,从组分质量分数中去解耦密度,则关于组分概率密度函数可变为
PC(C1,C2,…Cns)=Pρ(ρ)Pf(f1,f2,…,fns)
(11)
通过假设密度的概率密度函数是一个δ函数,进一步简化问题:
(12)
按照S.S.Girimaji[12]提出了一种多元β-PDF模型计算湍流混合中的组分质量分数
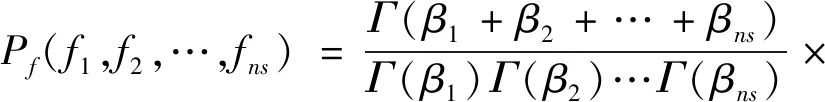
(13)
式中:
(14)
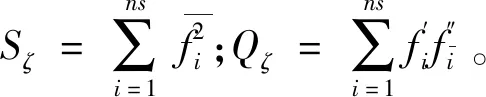
Qζ为组分方差的和,是个一类似于湍动能的湍流标量能量,其数学约束为Qζ≤1-Sζ。
式(14)保证了βi的值是非负。当只有一种组分的质量分数非零时,Sζ=1,这种约束具有物理修正限制。
1.3 数值方法
控制方程为多组分湍流N-S方程,时间推进采用对角化近似隐式格式,湍流模型为SST模型,加入了Wilcox的壁面函数,无黏通量的求解使用了低耗散的Edwards通量分裂格式,采用三阶MUSCL插值来提高计算精度,使用的化学反应机理为C.K.Westbrook等[13]提出的CH4和C2H4七组分四方程化学反应,二者的摩尔比例为64%和36%。
1.4 模拟工况
在A.M.Storch等[9]的报告中,模拟飞行马赫数为5.84的试验结果和计算结果最全面,因此本文主要针对这个状态开展计算,具体参数如下:模拟飞行马赫数为5.84;喷管出口马赫数为2.51;驻室总温为1 550 K,总压为1.48 MPa;P1喷嘴当量比为0.15,S1喷嘴当量比为0.5。
2 计算结果分析
CFD++、VULCAN与AHL3D计算的壁面压力模拟结果如图3所示,并与文献[11]所提供的实验结果进行了对比,其中x为隔离段/燃烧室流道长度。三者结果的曲线趋势基本一致,CFD++没有得到激波串结构,这可能是计算时没有连着前面的喷管一起计算造成的。但与试验结果相比,P1喷嘴到燃烧室位置两者压强有明显差别,都没能正确模拟P1喷嘴前的压强波动和压强爬升位置。
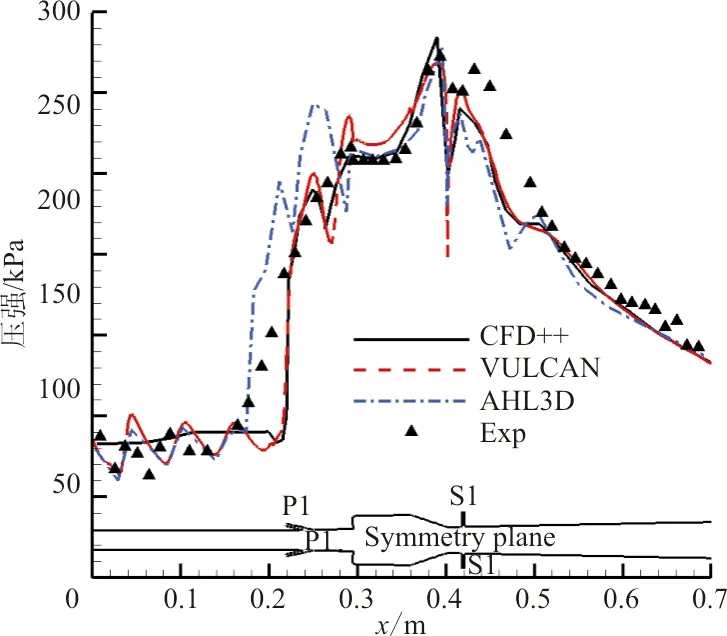
图3 CFD++、VULCAN和AHL3D的计算结果Fig.3 Computation results of CFD++, VULCAN and AHL3D
2.1 HF2直连式超燃冲压发动机计算验证
在开展燃烧流场计算验证之前,首先进行网格无关性验证。流向网格数保持不变,研究不同法向壁面网格数(ny)对壁面压强的影响。法向网格数分别取31、41、51和61四种分布,为减少计算量,此处仅对冷流流场进行验证。法向网格数对壁面压强分布的影响示意图如图4所示,可以看出:壁面压强分布基本一致,达到了网格无关性。
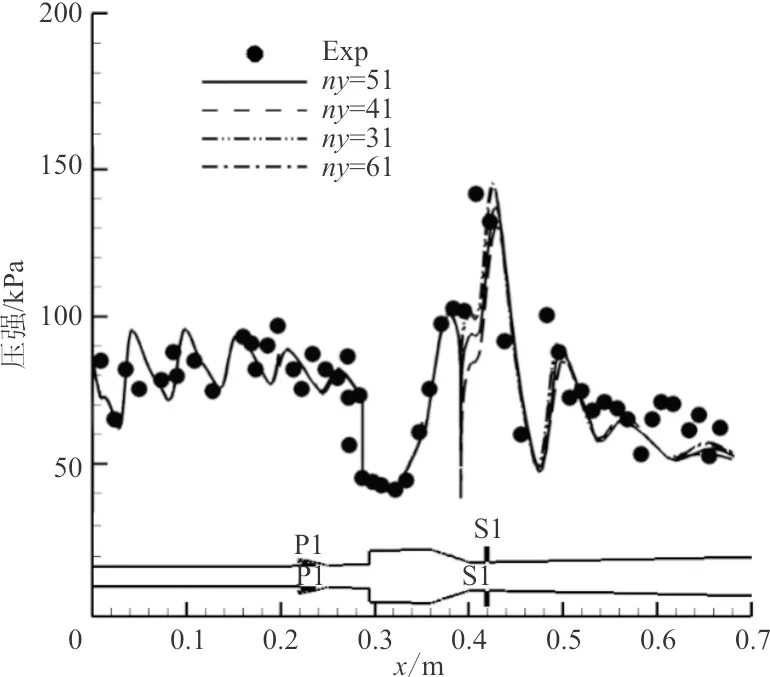
图4 法向网格数对壁面压强分布的影响Fig.4 Effect of normal direction grid number on wall pressure distribution
不用燃烧模型的有限速率化学反应壁面压力模拟结果如图5所示,并与文献[11]所提供的计算结果和实验结果进行了对比。从图中可以看出,在隔离段入口往后,壁面压强分布先是出现了明显的激波串结构,流动压力损失表现得非常明显,然后在P1喷嘴处出现了压强升高。随后压强逐渐上升,在凹槽位置出现了一个台阶,这是由于凹槽的长深比为3.8,是典型的开式凹槽流动。在凹槽后缘,由于后缘出现了压缩波,导致压强进一步上升,在凹槽后面由于流道扩张,导致压强下降。在S1喷嘴的位置,由于喷流的压强比较高,壁面压强分布出现了又一个峰值,在这以后压强分布逐渐下降。虽然压强曲线趋势正确,但与实验和文献结果相比,计算结果的整体压强偏低,在P1喷嘴和燃烧室位置尤为明显。
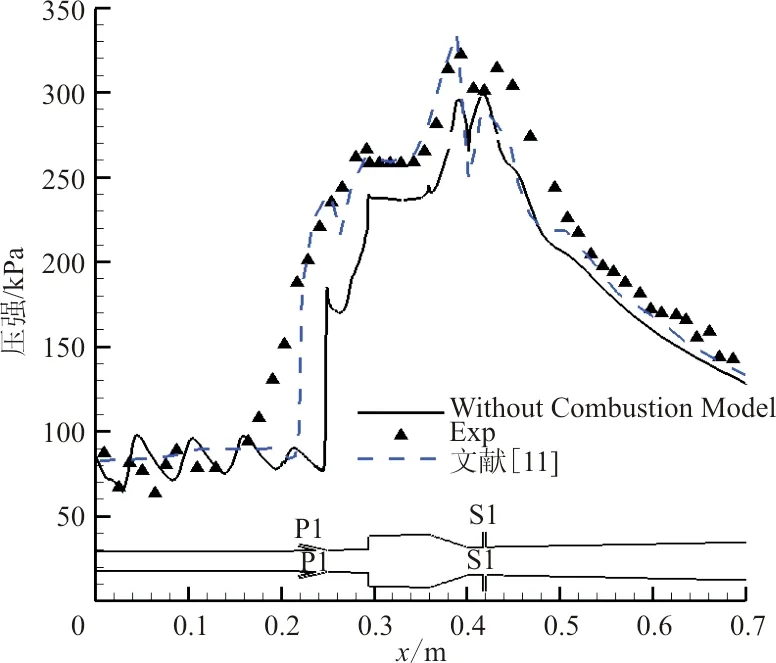
图5 RANS计算的结果Fig.5 Computation result of RANS method
2.2 PDF模型对化学反应的影响
采用不同的PDF模型对湍流燃烧进行影响而模拟的壁面压力模拟结果如图6所示,可以看出:在采用PDF模型后,P1喷嘴到燃烧室位置的压强曲线有明显升高,与实验结果吻合较好。这表明在所设定的计算条件下,采用设定型PDF模型能更好地模拟湍流对化学反应的影响,相应的化学反应也较为充分。
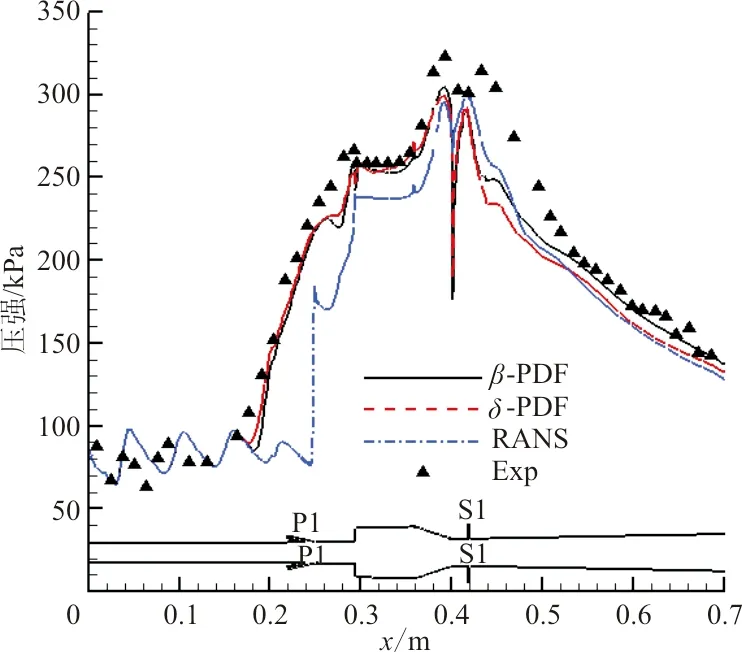
图6 PDF模型对壁面压强分布的影响Fig.6 Effect of PDF models on wall pressure distribution
两种PDF模型的压力结果比较接近,压升位置基本一致;从P1位置到0.4 m即燃烧室收缩段结束位置,β-PDF的壁面压力峰值高于δ-PDF模型,与实验结果吻合较好;在0.4 m位置处,两者压强都有明显的下降,但δ-PDF模型的下降梯度要远高于β-PDF模型;在0.5 m位置处,两种PDF模型压强曲线有一个平滑下降段。
隔离段流场云图如图7~图8所示,可以看出:在隔离段的流动中存在一组激波串,二者的激波串基本吻合。
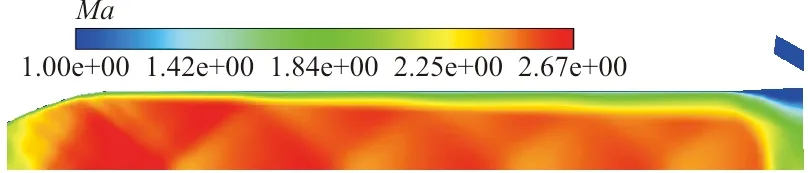
图7 β-PDF模型隔离段流场云图Fig.7 Flow field of isolator for β-PDF model
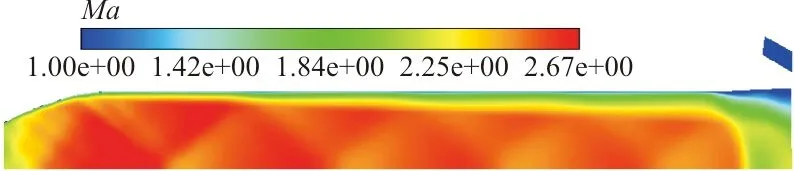
图8 δ-PDF模型隔离段流场云图Fig.8 Flow field of isolator for δ-PDF model
RANS和两种PDF模型在P1喷嘴处以及燃烧室的流场云图和CO2分布图如图9~图10所示。
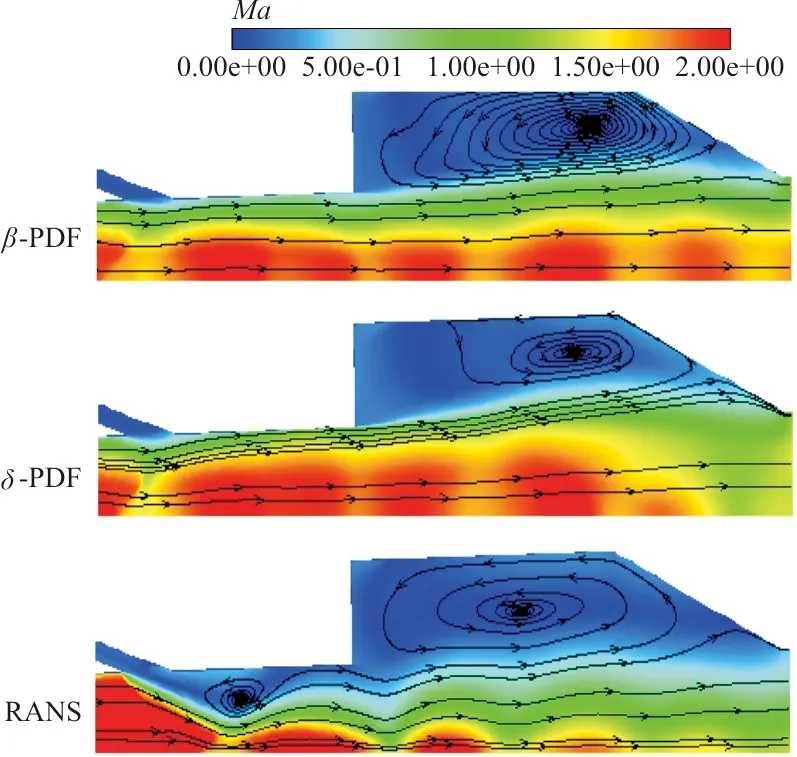
图9 三种模型P1喷嘴和燃烧室流场云图Fig.9 Flow field of P1 injet and combustor with three models
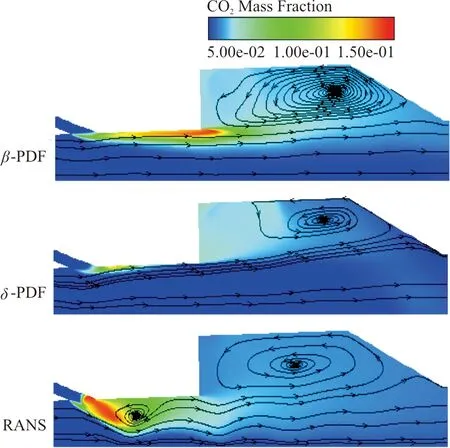
图10 三种模型P1喷嘴和燃烧室CO2分布Fig.10 CO2 distribution of P1 injet with three models and combustor
结合图6壁面压强分布对比可知,采用PDF模型的压升位置要提前于RANS,与实验结果吻合较好,原因是RANS模拟结果在P1燃料入口附近下游区域生成了一个旋涡,在这个旋涡前产生一道斜激波,因此P1附近压力有较大的变化。采用CFD++和VULCAN也有同样现象,激波更靠近P1喷嘴位置,但压升位置仍比实验和AHL3D的结果偏后,原因是由于燃烧产生的反压导致分离区前传的距离不够引起的,这与计算所采用的化学模型、湍流施密特数有关。而从图10可以看出,在燃烧室中也存在一个旋涡,该旋涡使燃料在燃烧腔内得到充分混合和燃烧,使得燃烧室压强迅速上升。整个燃烧室区域湍流脉动较为剧烈,它和燃烧相互作用加剧了反应,使得不考虑湍流燃烧相互作用的有限速率反应模型预测的燃烧剧烈程度偏小,而考虑化学平衡的PDF模型预测的燃烧主要在燃烧室里发生,在P1喷嘴附近预测的燃烧区域偏小,没有形成漩涡,这对全流场的预测与实验符合较好。
S1喷嘴处流场云图如图11~图12所示,燃料的垂直入射使得燃料得到更加充分的混合,使得燃烧化学反应更加迅速。这些现象都与实际产生的物理化学现象是一致的,也与图6的压强曲线一致。
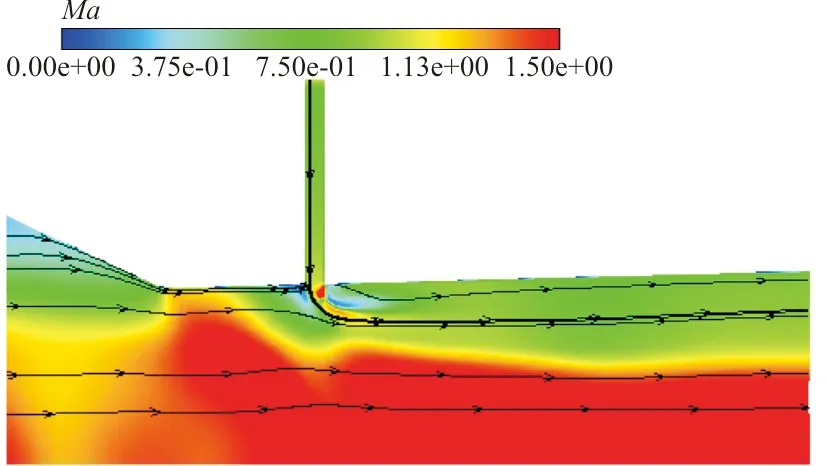
图12 δ-PDF模型S1喷嘴流场云图Fig.12 Flow field of S1 injector with δ-PDF model
总的来看,计算结果与实验和文献[11]结果大致相当,说明本文所采用湍流燃烧模型及数值方法可用来模拟HF2直连式超燃发动机燃烧流场。
两种PDF模型计算结果的一维质量加权平均马赫数如图13所示,在坐标x=0 m即拉瓦尔喷管的尾部,计算得到的马赫数为2.5,而实验设计的马赫数为2.51,二者基本吻合。在x=0.22 m即P1喷嘴位置处采用PDF模型的马赫数有阶跃现象,位置比RANS提前了。这说明采用PDF模型在P1处的燃烧更加充分,因此对P1前段的流场影响增大了。在P1喷嘴下游区域,马赫数有剧烈下降,这与该处的压强激波相对应。对称面和横截面的马赫数分布云图如图14所示,马赫数在主喷嘴P1前在2.5左右,随着燃烧的发展,马赫数逐渐下降,在凹槽处接近亚声速,在凹槽后由于流道扩张,马赫数逐渐增加到2左右。两种模型的燃烧在0.3~0.45 m的是亚声速区域,而A.M.Storch等[9]的模拟结果中亚声速区域为0.35~0.5 m,这说明在来流马赫数为5.84时,HF2发动机处于双模态形式。
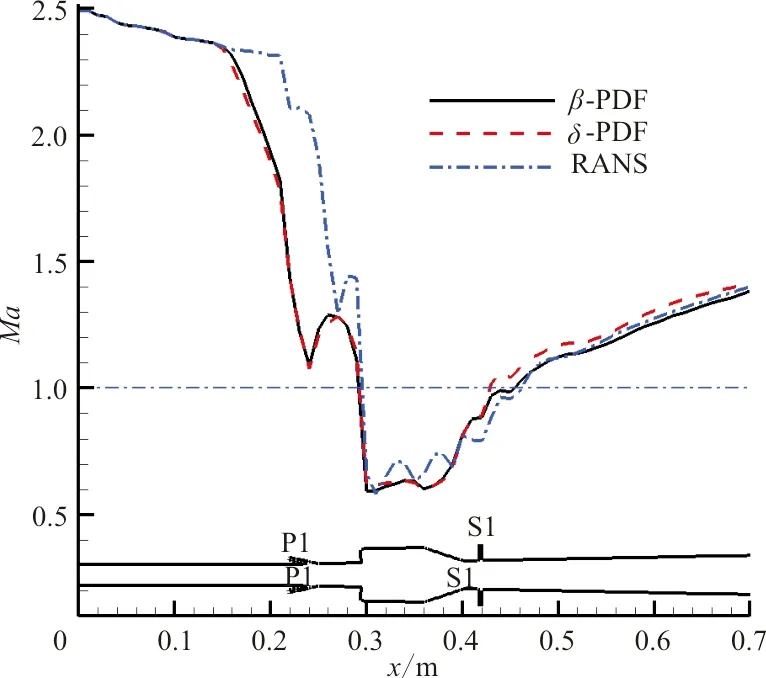
图13 一维质量加权平均马赫数分布Fig.13 One-dimensional mass weighted mean distribution of Mach number
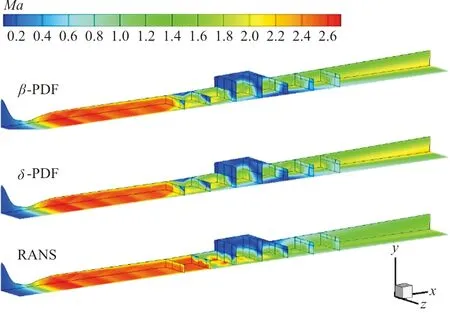
图14 对称面和横截面的马赫数分布Fig.14 Mach number distribution of symmetry plane and cross section
两种PDF模型计算结果流场总温的一维质量加权平均如图15所示,可以看出:在隔离段受壁面传热的影响,总温逐渐下降,于是总压也随之下降。在P1燃料喷嘴下游,总温迅速爬升,其原因是该处发生了燃烧反应,释放了大量热量使得总温上升。同样,在S1燃料喷嘴下游,总温也因为同样的原因而迅速爬升。这些现象都与实验现象相吻合。对称面和横截面的总温分布对比如图16所示,总温靠近z向壁面比较高,在z向对称面比较低,随着燃烧的发展,逐渐增加到3 000 K左右。可以看出,PDF模型计算得到的总温在燃烧室位置处比RANS的更高,表明采用PDF模型的化学反应速度快,燃烧释热多。
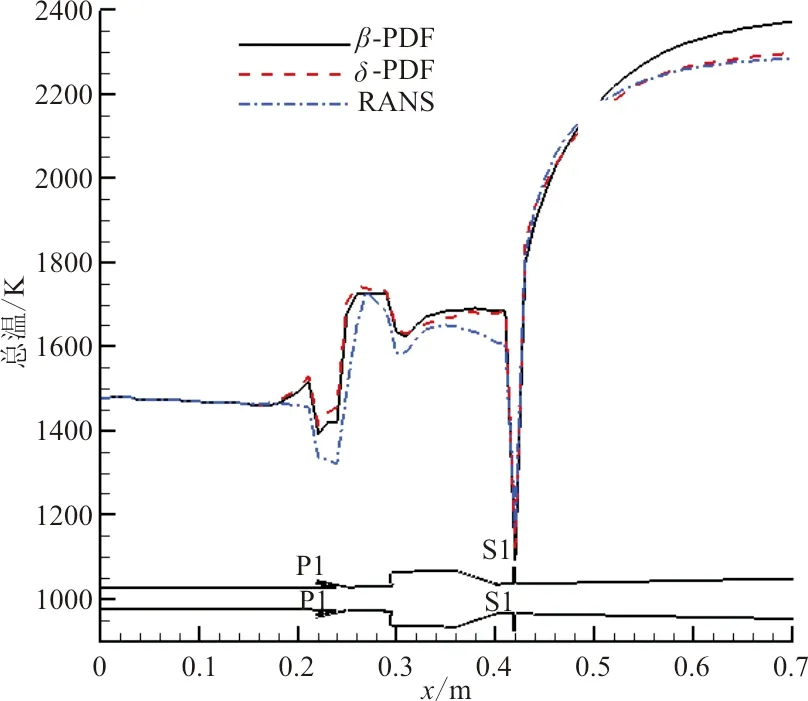
图15 总温一维质量加权平均分布Fig.15 One-dimensional mass weighted mean distribution of total temperature
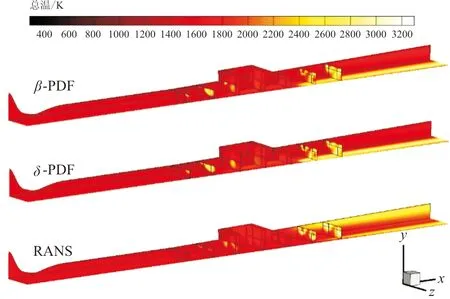
图16 对称面和横截面的总温分布Fig.16 Total temperature distribution of symmetry plane and cross section
2.3 PDF模型对燃烧效率的影响
对碳氢燃料燃烧效率的定义主要有两种,一种是根据燃料的消耗来定义,另一种是根据总温来定义。本文根据燃料的消耗来计算氢燃料的燃烧效率:
(15)
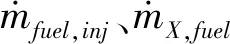
研究案例的燃烧性能结果如表1所示,其中η为燃烧效率,φ为油气比,可以看出:两种PDF模型都具有良好的燃烧效率。A.M.Storch[9]采用VULCAN和CFD++模拟的结果如表2所示,结果差异可能是因为不同的求解器采用不同机制来求解化学反应,导致燃烧效率的不同。
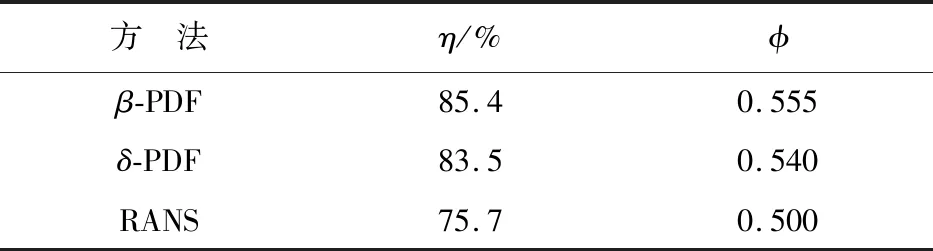
表1 燃烧效率Table 1 Combustion efficiency
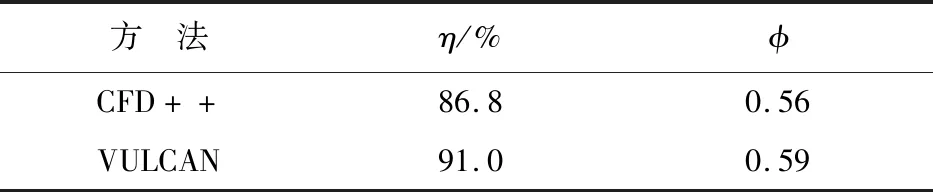
表2 VULCAN和CFD++燃烧效率Table 2 Combustion efficiency of VULCAN and CFD++
3 结 论
(1)在所设定的计算条件下,采用设定型PDF模型能更好地模拟湍流对化学反应影响,相应的化学反应也较为充分。
(2) 对于HF2直连式超燃发动机,采用δ和β分布设定型PDF模型对化学反应的影响会导致壁面压强、流场、一维质量加权马赫数、总温、燃烧效率等结果有所差别,但发展趋势一致,且对燃烧模态没有影响,β-PDF模型预测壁面压强分布与实验结果吻合更好,燃烧效率更高,更能够捕捉湍流对于化学反应的影响。
