基于Thomas 簇过程的异构蜂窝网能量效率分析

金明录，郭楠

（大连理工大学信息与通信工程学院，辽宁 大连 116024）

1 引言

近年来，人们对蜂窝数据的需求迅速增长，未来移动网络必将朝着异构的方向发展，即支持密集低功率小小区和低密度高功率基站共存。以用户为中心的小小区部署正在成为未来无线架构的重要组成部分[1]。随着世界经济的飞速发展，全球气候变暖和能源消耗不断加剧，节能减排绿色发展已经成为全球性的重要议题，通信基站节能是通信企业节能减排的重要前沿阵地。在异构蜂窝网（HCN,heterogeneous cellular network）基站部署阶段需要更多地考虑能量消耗的问题，因此为了减少功率消耗，最近的很多研究都基于泊松点过程（PPP,poisson point process）空间模型来设计基站休眠算法[2]和参数优化方法[3-4]。

常见的分析蜂窝网络的数学工具是随机几何理论，使用PPP 随机且独立地建模基站和用户设备的位置。文献[5]在PPP 模型下，结合偏置接收功率的小区扩展的关联策略，推导出下行信道的中断概率和平均吞吐量。文献[6]考虑超密集部署小基站，在最大平均接收功率的连接策略下，得出基站部署的各个参数与能量效率的关系。然而，上述方法假设基站和用户设备的位置是完全独立的，这并不十分准确。实际中，在住宅区、商务办公区、重大活动中心等位置，用户很容易出现聚簇，导致基站和用户之间有相关性。无线网络中，一些用户通常会聚集的特定区域被称为用户热点区域。针对移动用户的聚簇分布问题，可以使用泊松簇过程（PCP,poisson cluster process）来建模，这样更加接近真实通信场景。因为PCP 可以捕获邻近点之间的吸引力，所以也被扩展在很多其他的应用场景中，如毫米波通信[7]和D2D（device to device）通信[8]。文献[9]分别推导了用户服从Thomas 簇过程和Matern 簇过程的覆盖概率，但是没有考虑小区扩展可以给网络能量效率带来增益。不同于用户分布模型PCP[7,9]，文献[10-11]将小基站建模为 PCP，在一个三层HCN[10]中，建模每一层基站为Neyman-Scott 簇过程，基于最大瞬时信号干扰噪声比的小区选择机制得到中断概率的表达式。小基站服从Matern 簇过程，文献[11]得到中断概率及数据速率的表达式。

在近年的研究工作中，文献[12-14]受3GPP 启发，开发了PCP 和PPP 建模用户-基站的统一框架。与其相似，本文也给出了用户-基站耦合的模型框架，不同之处在于本文是基于最大平均偏置接收功率（max-BRP,max mean bias received signal power）的关联策略，而文献[12]考虑最大信号干扰比（SIR,signal to interference ratio）关联，文献[13]考虑最大功率关联。在max-SIR 关联中，不必考虑用户到服务基站的距离分布。本文提供了典型用户覆盖概率的易于计算的表达式和精确分析，即在覆盖概率的完整表达式上做出了贡献。文献[15]假设宏基站模型为PPP，小基站和用户根据不同的函数成簇分布。与文献[15]设置不同的是，本文认为未来5G 网络中，小基站的密集部署不仅是在人员密集的场所，在宏小区的边缘同样需要部署更多的小基站来提高小区的覆盖性能和边缘用户的通信质量，增加网络的容量。小基站具有灵活性，可在任意地方部署，因此，小基站的分布近似于均匀PPP，由此可知本文的设置是合理的，也是易于分析的。同时，本文的模型可以扩展到基于最近基站关联策略[14]的网络中，得到此时的关联概率和覆盖概率。本文给出了网络能量效率的定义，并在仿真分析部分与最近基站关联策略进行比较。从结果上看，max-BRP 关联策略在提高能量效率上有一定的优势。本文的创新点如下。

1)本文给出了以用户为中心的用户热点模型框架，利用Thomas 簇过程建模小基站内的用户位置，应用max-BRP 关联策略均衡宏基站和小基站的负载，该策略鼓励宏基站用户与负载较轻的小基站相关联，减少功率消耗，增加网络容量。

2)本文利用随机几何理论和概率论推导出典型用户的关联概率、覆盖概率和整个网络的能量效率。本文的数学推导具有一般性，可以扩展到基于最近基站的关联策略上。

3)本文给出了K层HCN 基于PCP 模型的详细数值分析。为了验证分析，将数值计算结果与蒙特卡洛仿真结果进行了比较，证明了本文分析是正确的。同时，比较了max-BRP 关联策略和最近基站关联策略下的能量效率，结果表明max-BRP 关联策略在提高能量效率上有一定的优势。

2 系统模型

考虑一个K层的下行HCN，每一层基站的分布都是独立同分布的PPP，第k层基站的部署依据密度为λk的均匀PPPΦk进行建模。假设用户以一个特定的小小区基站为中心成簇分布，用户的位置是该基站的一个子点过程，建模为Thomas 簇过程Φu，在第κ(κ=1,…,K)层网络中，假设每个小小区基站周围有n个用户，且服从方差为的高斯分布。用户位置用向量z表示，则向量z的概率密度函数（PDF，probability density function）为

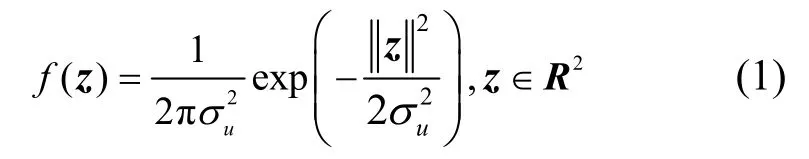
为了分析方便，假设典型用户处于原点，用户所在的小小区基站标记为第0 层，记K={0,1,…,K}，k∈K，平面上所有基站的集合表示为信号经历大尺度路径损耗和小尺度瑞利衰落信道，在典型用户的位置上，来自服务基站的接收功率为BkPkhk||x||-α。其中，Bk表示第k层偏置因子，偏置因子的设置影响着用户更愿意接入哪一层网络中，当Bk=1 时，当前网络无偏置，当Bk＞1 时，小区覆盖范围得到扩展；Pk为第k层基站的信号传输功率；hk为小尺度衰落系数；x为基站的坐标，||x||为典型用户与服务基站之间的欧氏距离；α(α＞2)为路径损耗指数。在瑞利衰落下，hk～ exp(1)。典型用户根据max-BRP来选择关联的基站，则服务基站的位置x*表示为

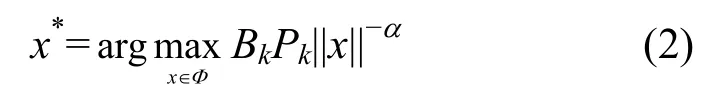
值得注意的是，在没有小尺度衰落的情况下，就欧几里得距离而言，在第k层网络中，候选服务基站将是最接近典型用户的基站。用户在平面上与基站的距离是通信的关键影响因素，假设典型用户与第k层候选服务基站之间的欧氏距离为rk。r0服从瑞利分布，其PDF 和互补累积分布函数（CCDF,complementary cumulative distribution function）分别为

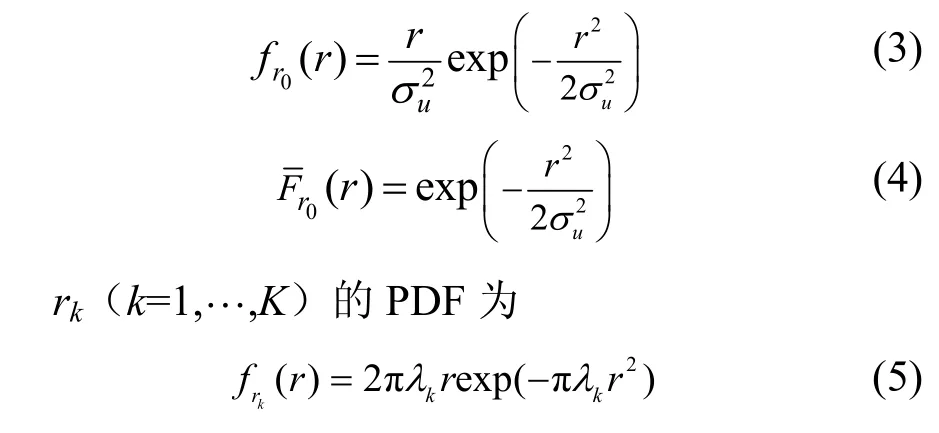
考虑干扰受限网络，忽略噪声影响。假设典型用户与服务基站的距离为Rk，则认为此变量是用户在关联到第k层的条件下的服务距离，典型用户接收到的第k层服务基站xk的SIR 为

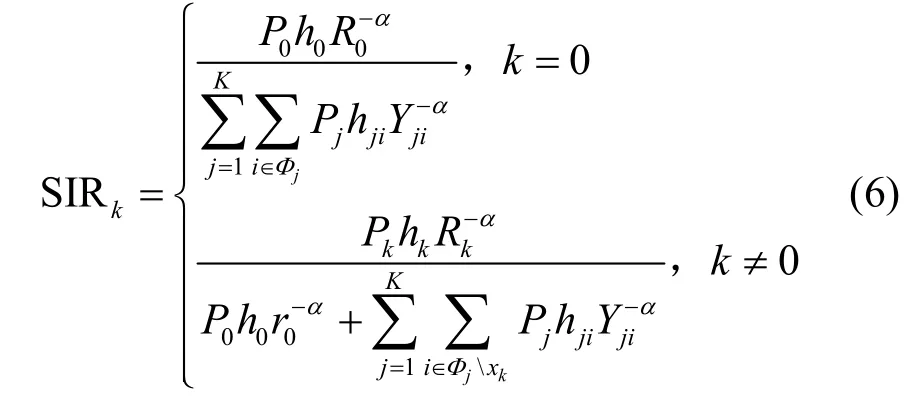
其中，j表示第j层网络，i表示第i个基站，Yji表示典型用户到第j层第i个基站的欧氏距离。

3 覆盖概率

本节重点关注网络异构拓扑下的覆盖概率。网络中覆盖概率的定义为用户成功解码基站下行信号的概率，数学上可表示为Pr(SIR＞β)，其中β为SIR 的阈值门限。覆盖概率是衡量网络性能的一个重要通信指标，对覆盖概率取对数可以得到平均数据速率，此时覆盖概率可以解释为平均数据速率γ(β)=lb(1+β)可达的概率。首先，推导典型用户被第k层基站服务的关联概率；然后，推导关联第k层的条件下，典型用户与服务基站之间距离的PDF；最后，得到选定关联层和此关联层基站成功解码用户数据的联合概率，定义网络总覆盖概率为所有层的联合概率之和，据此推导出覆盖概率的精确表达式。

定理1在K层HCN 用户热点地区中，第k层网络的关联概率为

分别考虑k=0 和k≠0 这2 种情况。当k=0 时，有

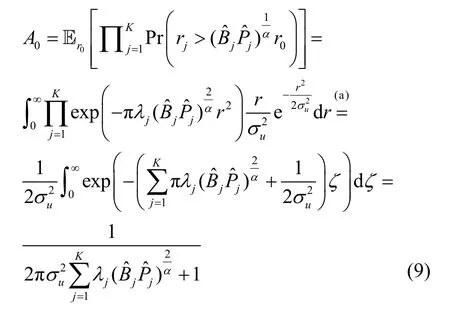
其中，步骤(a)进行变量代换，ζ=r2。

当k≠0 时，有

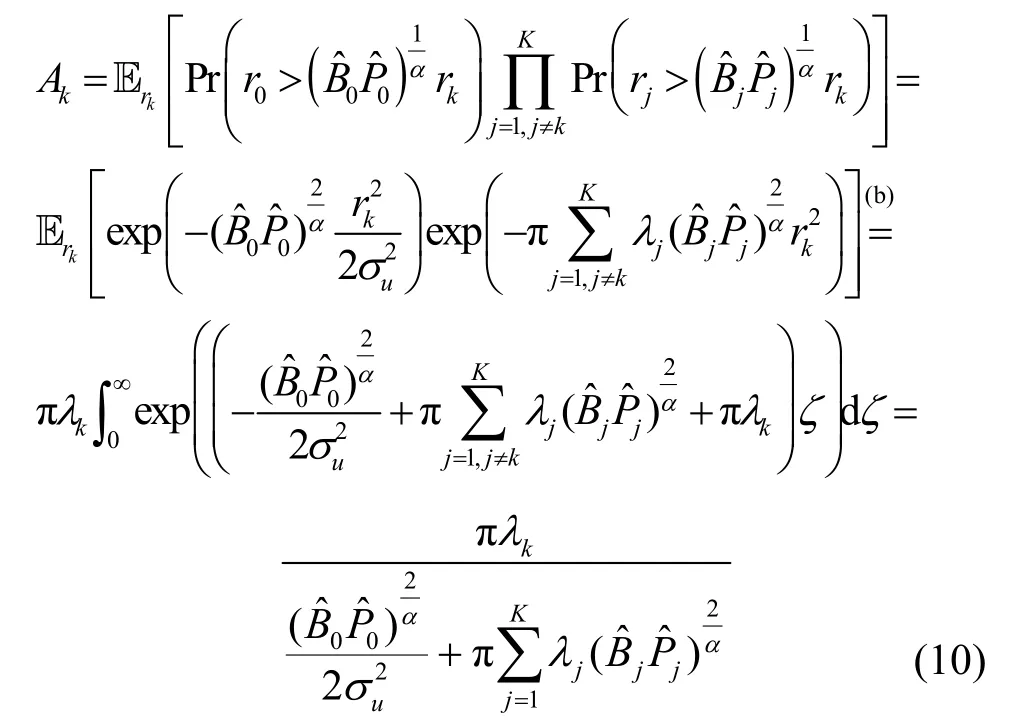
其中，步骤(b)同样进行了变量代换ζ=r2。

证毕。

从定理1 可以看出，用户选择的关联基站与其所处的平面拓扑结构强相关。用户分布方差、基站密度、信号发送功率、偏置因子和路径损耗程度都影响着用户的基站选择。

引理1典型用户与其服务基站之间距离Rk的PDF 为

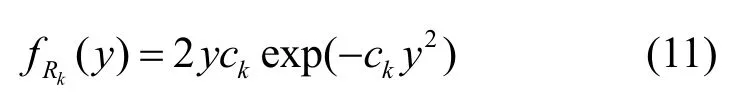
证明Rk被认为是用户在关联到第k层的条件下的服务距离，所以，Pr(Rk＞y)=Pr(rk＞y|{Ak})=，其中，{Ak}记为用户关联第k层的事件。联合概率为

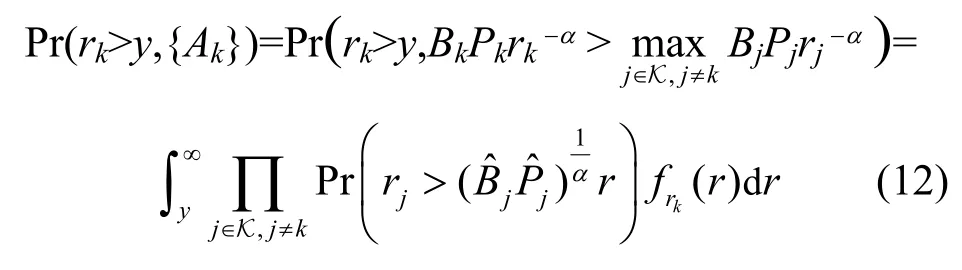
分别考虑k=0 和k≠0 这2 种情况。当k=0 时，有

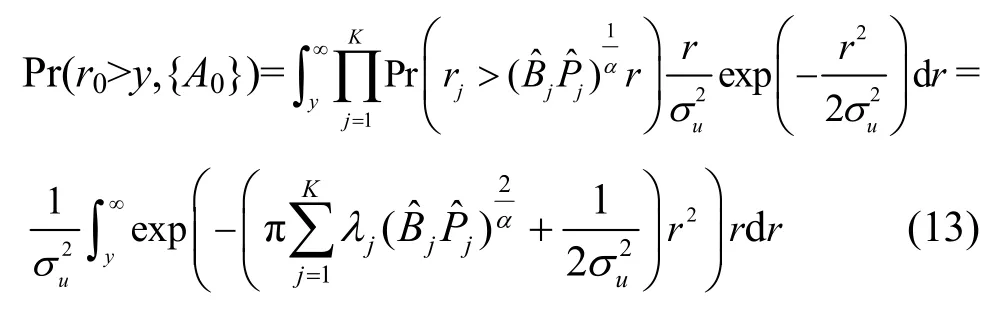
由式(13)和A0可以推导出R0的CCDF，对其求导得到的PDF 表达式为

当k≠0 时，有

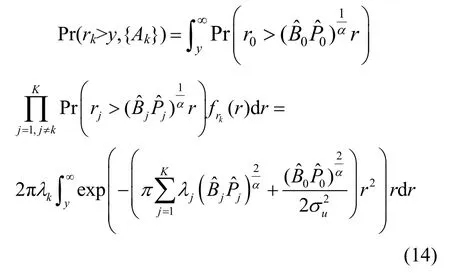
同理，可以得到Rk(k≠0)的 PDF 为

结合2 种情况，整理可得引理1。

证毕。

定理2在K层HCN 中，用户建模为小基站的子点过程，且用户与提供最大平均偏置接收功率的基站相关联，每层网络的覆盖概率和网络总覆盖概率Pcov(β)的精确表达式为

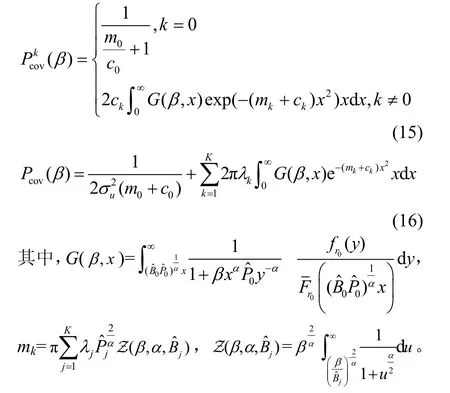
证明引入随机变量Ik表示第k层网络的干扰信号，则各层的覆盖概率为

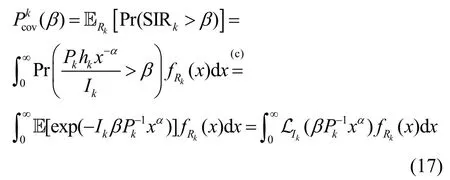
其中，步骤(c)的依据是hk服从均值为1的指数分布，LI(s)是在s处评估的随机变量I的拉普拉斯变换，定义式为LI(s)=E[e-sI]。当k=0 时，令，则有

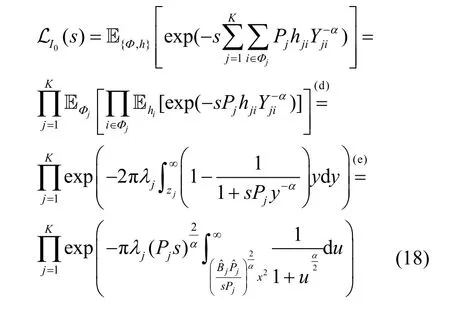
其中，步骤(d)是根据概率生成函数（PGFL,probability generating functional）得到的，第j层最近的干扰源的距离至少是；步骤(e)中进行了变量代换，干扰的拉普拉斯变换整理为

将式(19)和式(11)代入式(17)，得到一个简单的表达式。当k≠0 时，令，有

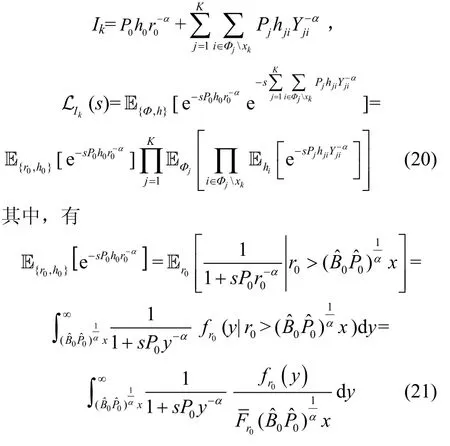
服务基站位于第k层，所以第0 层的基站变成了干扰源，干扰距离大于，结合式(3)和式(4)，有，其中，

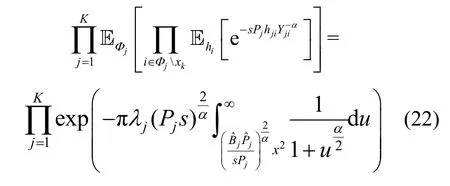
式(22)的推导过程与式(18)相同，进一步整理得到

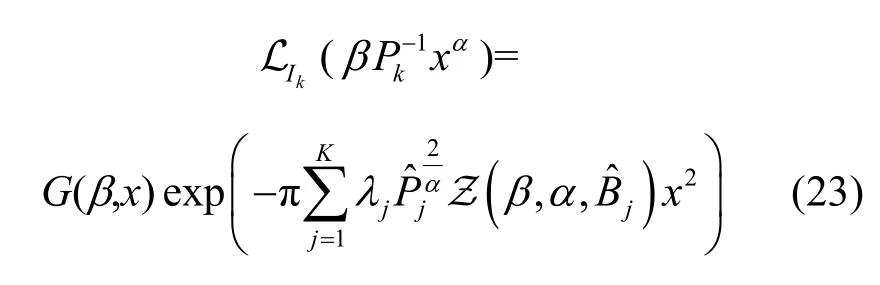
最后，将式(23)与式(11)代入式(17)，即可证得每层网络的覆盖概率。根据网络的总覆盖概率定义式，可以很容易地得到式(16)。

证毕。

4 能量效率

对于任何通信系统，信道容量都是非常重要的度量指标。本节将重点研究典型用户在K层HCN中可实现的遍历速率和覆盖下的平均数据速率，并通过信道容量得到能量效率这一衡量指标。

1)遍历速率（平均数据速率）

遍历速率表示所有信道状态的平均数据速率，具体用在快衰落信道中。本文假设使用了容量可实现编码，因此香农容量可达。香农公式为γk=lb(1+SIRk(xk))，单位为bit/(s·Hz)，记χ=SIRk(xk)为第k层服务基站提供的SIR，可以通过求期望得出遍历速率为

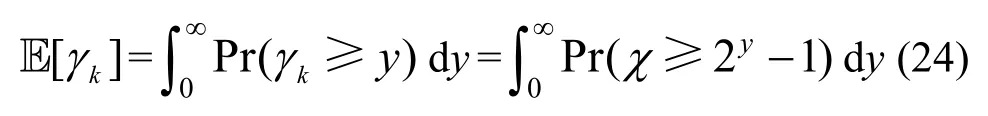
因此，求χ的CCDF 是推导遍历速率的关键。

2)覆盖下的平均数据速率

在已经获取覆盖或中断信息的前提下，运营商希望知道可以向覆盖范围内的用户提供的平均数据速率。根据香农公式，用户覆盖下的平均数据速率定义为单位为bit/(s·Hz)，其中，表示用户处于第k层覆盖范围内（用户可以成功解码下行数据）的事件。

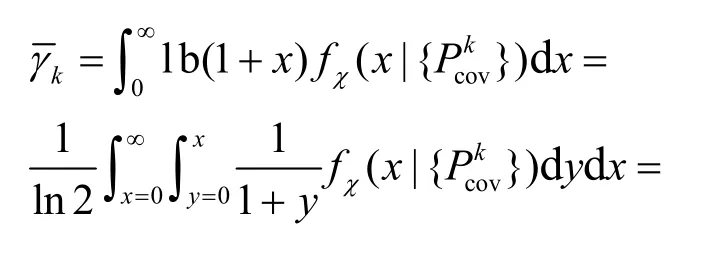
命题1在K层HCN 中，第k层遍历速率（平均数据速率）为

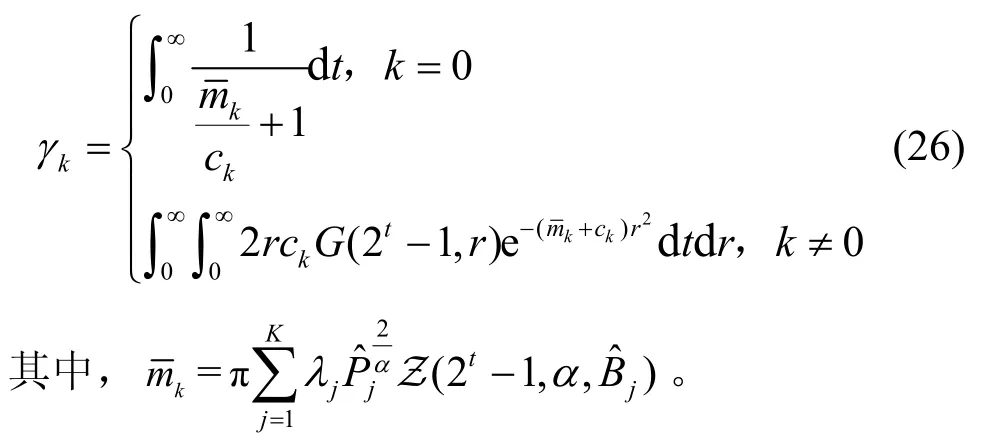
证明遍历速率是在已知与第k层网络关联的条件下求香农公式，所以有

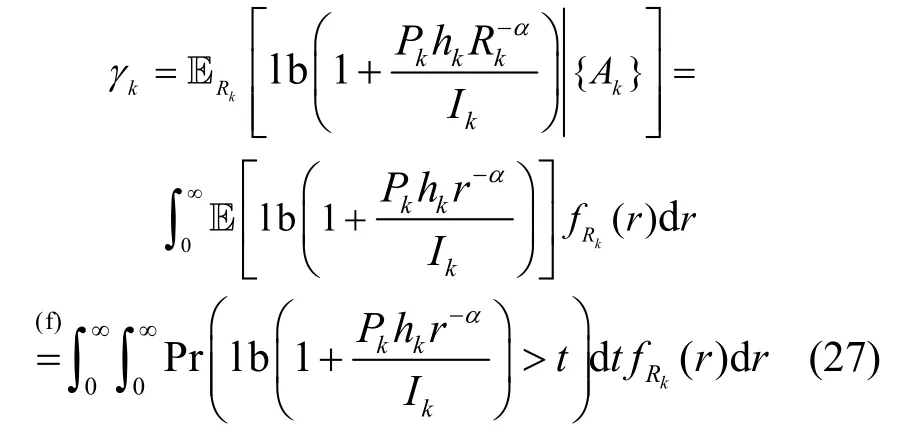
从式(28)可以看出，将式(17)中变量β替换为2t-1，根据类似的推导过程，可直接得到干扰的拉普拉斯变换为

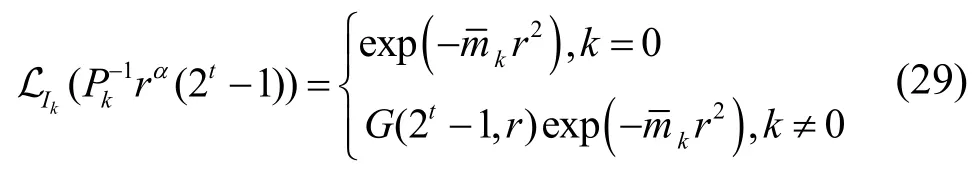
将式(29)代入式(27)即可证得命题1。

证毕。

命题2在K层HCN 中，已知用户处于第k层覆盖范围内，则平均数据速率为

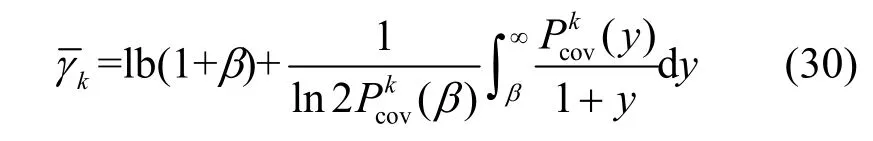
证明根据平均数据速率的定义式，有

对式(25)进行分段积分，即可得到式(30)。

证毕。

在异构蜂窝网络中，第k层基站的功率消耗模型由两部分组成，分别是静态功率消耗P0k和发射功率消耗Pk，其中，静态功率消耗包括基站的信号处理进程、电池备份和设备冷却等，发射功率消耗与静态功率消耗是互相独立的两部分。根据系统模型，每个基站的总功率消耗可以表示为Pk=P0k+ξkPk，其中，ξk代表与基站的流量负载正相关的功耗系数，所以有ξk=。全网平均网络吞吐量定义为，能量效率被定义为平均网络吞吐量与平均网络功耗之比，如式(32)所示，单位是bit/(J·Hz)。

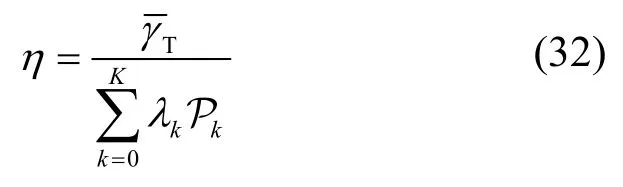
5 仿真分析

本节对系统模型及推导的表达式分别采用蒙特卡洛及数值积分的方法进行仿真分析，使用的仿真工具是Matlab。宏基站为第一层，其他层为微基站、微微基站和毫微微基站等小基站。仿真区域是半径为3 000 m 的圆形区域，蒙特卡洛次数为4 000 次。没有特殊说明时，仿真参数如下：小基站用户数n=10，路径损耗指数α=3，基站密度（单位为m-2）λ1=4×10-6m-2，λ0=λ2=5×10-5m-2，基站静态功率P00=P02=6 W，P01=130 W，各层偏置因子为1。

图1 为用户关联概率与用户分布标准差（代表簇的大小）的关系，仿真参数为K=κ=2，P1=226.4 W，P0=P2=12.22 W，仿真结果和数值结果的重合验证了推导的关联概率式是精确的。可以看出，随着簇越来越大，用户越来越分散，第0 层基站服务用户的概率越来越小，当σu大于75 时，关联概率变为最小。而第2 层基站服务用户的概率一直大于第1 层，这是因为小小区基站密集部署于用户周围，宏基站距离用户很远，小基站的信号经历的大尺度衰落远比宏基站的小，所以用户有更大的概率选择关联小基站。当σu→∞时，可以认为簇大小趋于无穷，在整个平面上呈现高斯分布（近似PPP 分布），相当于用户没有集群分布，此时关联概率趋于一个常数。

图1 用户分布标准差对各层关联概率的影响

图2 为不同簇大小对覆盖概率的影响，仿真参数为K=κ=2，P1=226.4 W，P0=P2=12.22 W，β=1。同样可以看出，仿真结果紧密地贴合数值结果，证明了覆盖概率式的正确性。图2 中第0 层的覆盖概率最大，其他层的覆盖概率理论曲线相重叠，说明了基站PPP 模型下的覆盖概率与k和基站密度无关。全网的覆盖概率Pcov在σu很小时趋向于第0层；当σu逐渐增大时，由于第0 层关联概率减小，全网覆盖概率趋向于非0 层；当σu→∞时，全网覆盖概率则与非0 层覆盖概率一致，该结论可参考文献[5]的推论2。

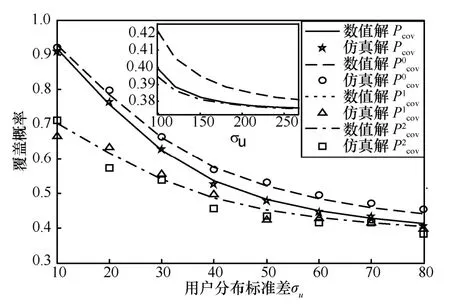
图2 用户分布标准差对覆盖概率的影响

图3 给出了不同α对网络关联概率和覆盖概率的影响。图 3(a)中的仿真参数为K=κ=3，，λ2=5λ1，λ0=λ3=10λ1，P1=200 W，P2=2 W，P0=P3=0.2 W，σu=50。第0 层的关联概率随着α的增大迅速提高，第2、3 层的关联概率也小幅度地相应增加，而第1 层关联概率快速减小。根据定理1 分析可知，具有最大发送功率的宏基站层随着α增大，关联概率会大幅度减小，而具有最小发送功率的第0 层和第K层的关联概率会随着α的增大而有所提高。图3(b)中的仿真参数为K=κ=2，σu=50，P1=226.4 W，P0=P2=12.22 W。首先，可以看出第0 层覆盖概率高于其他层，非0 层覆盖概率重叠在一起，原因是每一层基站都服从PPP 分布，随机用户有相同的SIR 分布。其次，图3(b)中比较了max-BRP 和最近基站2 种关联模型下的覆盖概率，可以看出当β＜10 dB 时，max-BRP 的全网覆盖概率更高，随着β变大，最近基站关联下的覆盖概率逼近本文所用模型下的覆盖概率。最后可以看出，网络的整体覆盖概率随着α的增大而增加，这是因为当大尺度衰落变大时，用户在平面中受到来自非服务基站的干扰会大幅减小，有用信号的损失小于干扰减小，所以在高楼林立、树木葱郁且地形复杂的城市中，热点地区的网络性能最终会得以提高。

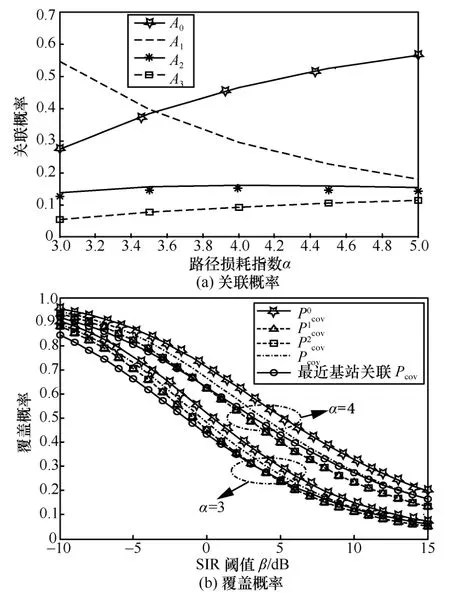
图3 不同α 对关联概率和覆盖概率的影响

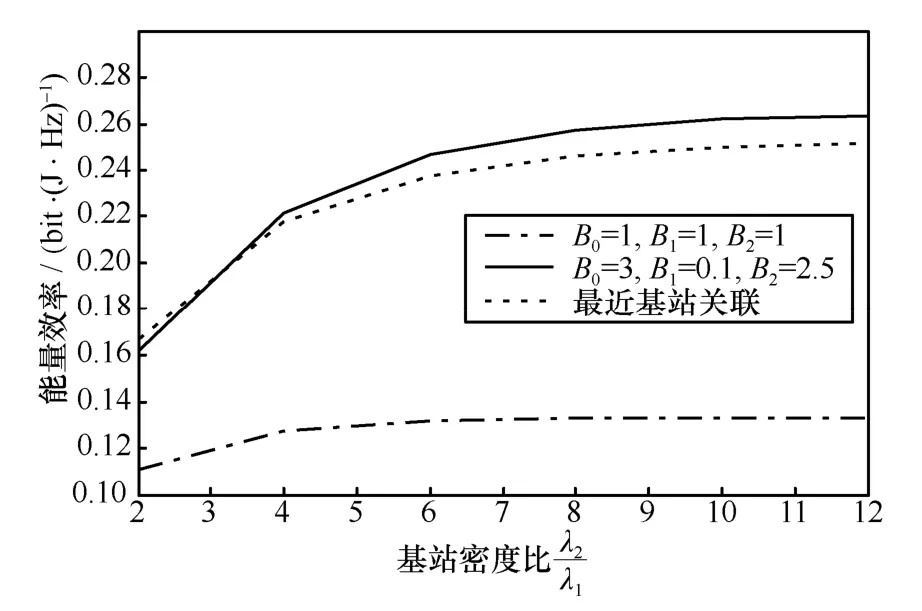
图4 对两层HCN 能量效率的影响

6 结束语

本文在以用户为中心的HCN 中，主要研究了热点地区的覆盖概率和能量效率。假设用户服从Thomas簇过程，随机选取一个用户，采用max-BRP 进行通信，推导出该用户的关联概率、覆盖概率，以及整个网络的能量效率表达式。然后通过数值仿真分析，验证了表达式的准确性，说明了本文的推导工作可以给未来的网络部署提供理论指导。最后仿真结果表明，与最近基站关联相比，设置合适的偏置因子，可以使用户更多地接入低功率小基站，提高无线资源利用率，进而大大提高网络的能量效率，达到绿色通信的目的。