基于复数支持向量回归机的盲均衡算法

杨凌，陈亮，赵膑，张国龙，李媛

（兰州大学信息科学与工程学院，甘肃 兰州 730000）

1 引言

自1975 年Sato[1]提出盲均衡的概念后，盲均衡理论和方法得到了学术界广泛的研究。其中，Bussgang 类盲均衡算法，如常模算法（CMA,constant modulus algorithm）[2]、多模算法（MMA,multi-modulus algorithm）[3-4]等，因其原理简单、易于实现、稳健性好、对不同系统的适用性强等优点而得到广泛应用[5]。近年来，统计学习理论广泛用于通信系统的数字信号处理，基于统计学习的方法被用来建立滤波器与输入数据之间的回归关系[6]。

支持向量机（SVM,support vector machine）[7]是建立在统计学习理论基础上的一种机器学习方法[8]，其已成为一种处理涉及非线性的分类和回归问题的流行工具[9]。Santamaría 等[10]首次提出将常模信号的误差函数代入支持向量机的框架，用迭代重加权二次规划（IRWQP,iterative reweighted quadratic programming）方法实现了线性信道下实数和复数信号以及非线性信道下实数信号的批量盲均衡。Lázaro 等[11]提出用迭代重加权最小二乘（IRWLS,iterative reweighted least square）方法求解线性信道下支持向量回归机盲均衡器的抽头系数，极大减少了计算复杂度。Sun[12]结合CMA 提出了基于支持向量回归机的MIMO 系统盲源分离与均衡方法，并在文献[13]中进一步引入 MMA 加以改进，能较好地实现MIMO 系统线性信道下高阶QAM 信号的盲恢复。Giacoumidis 等[14]将文献[11]的算法应用于相干正交频分复用光通信（CO-OFDM,coherent optical orthogonal frequency-division multiplexing）系统，实现了单通道16QAM 信号和多通道QPSK 信号的盲均衡。上述基于支持向量回归机（SVR,support vector regression）的盲均衡算法处理复数信号时，首先进行实数化处理，然后在实数域的希尔伯特空间内对代价函数进行解析，并用实数核建立输入与输出映射关系的模型。然而，文献[9]指出，这种处理方式丢失了信号在复数域存在的几何特征。

针对上述算法处理复数信号的不足，本文提出基于复数支持向量回归机（CSVR,complex support vector regression）的盲均衡算法，将MMA 的误差函数代入CSVR 的框架构造代价函数，并结合广泛线性估计[15]建立均衡器输出信号与均衡器输入信号映射的回归关系，利用Wirtinger 微积分[16]直接在复数再生核希尔伯特空间对复数信号进行解析，求解代价函数的鞍点。为降低计算代价，采用IRWLS 方法确定均衡器的抽头系数[17]。

2 盲均衡系统模型

等效基带盲均衡系统框图如图1 所示。其中，sn表示信号源发送的长度为N的独立同分布调制信号（n=1,2,…,N）。信道模型为有限长冲激响应滤波器，表示为，Lh为信道长度。令υn表示发送信号经过信道时引入的高斯白噪声，发送信号经过信道之后可表示为

其中，*表示卷积。

均衡器的作用是构建一个逆滤波器，使

其中，wn表示均衡器抽头系数，δn表示单位抽样序列。

图1 等效基带盲均衡系统框图

均衡器输出信号yn为

在不考虑噪声的理想情况下，yn可以表示为

经过决策器判决之后，理想的输出信号zn为发送信号sn经过d时间单位的延迟。

实际应用中，由于均衡器抽头系数的长度Lw有限，并且均衡器输入信号xn总会含有噪声，一般不能获得输出信号zn的准确值。所以，需用yn和sn计算误差en，并根据en自适应调节均衡器抽头系数。

在发送信号xn未知的情况下，常用xn的先验信息，如二阶或高阶统计量估计en，并结合盲均衡算法调节均衡器抽头系数，即得到盲均衡器。

3 复数支持向量回归机

支持向量机的优势在于仅用较少的数据样本即可获得良好的统计规律，从而实现预测[18]。复数支持向量机是支持向量机处理复数信号的推广，具体数学描述如下。

假设训练序列数据具有如下形式。

其中，ϒ=Cv表示输入向量空间，× 表示向量的叉乘。因为zn是复数，所以可以写成实部和虚部相加的形式，即。这里，r 和i 分别表示复数的实部和虚部，j 表示虚数单位。同理，。通过特征映射ΦC，将数据从输入空间ϒ变换到复希尔伯特空间H，此时训练数据表示为

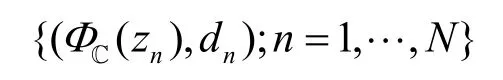
传统的复数线性回归函数为

其中，w∈H表示变量f的系数向量。

广泛线性估计函数为

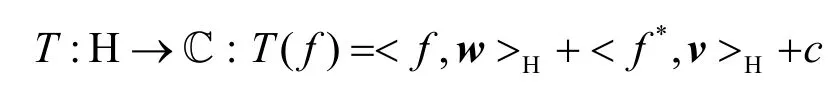
其中，w,v∈H，w和v分别表示变量f和变量f共轭的系数向量，c∈C。

不同于传统的复数线性回归函数，使用广泛线性估计函数对复数希尔伯特空间的数据进行回归，其优点是即使求解的回归函数T(f)在某一点的值与训练数据dn有ε大小的偏离，函数T(f)也会尽可能平滑[9]。

建立定义在输入空间ϒ的回归函数如式(5)所示。

类似支持向量回归机的结构，建立复数支持向量回归机框架如式(6)所示。

其中，C为惩罚因子，用于权衡经验风险和模型复杂度；ε为不敏感损失因子为非负松弛因子。

利用拉格朗日乘子法和KKT 条件将式(6)转化为如下的对偶问题。

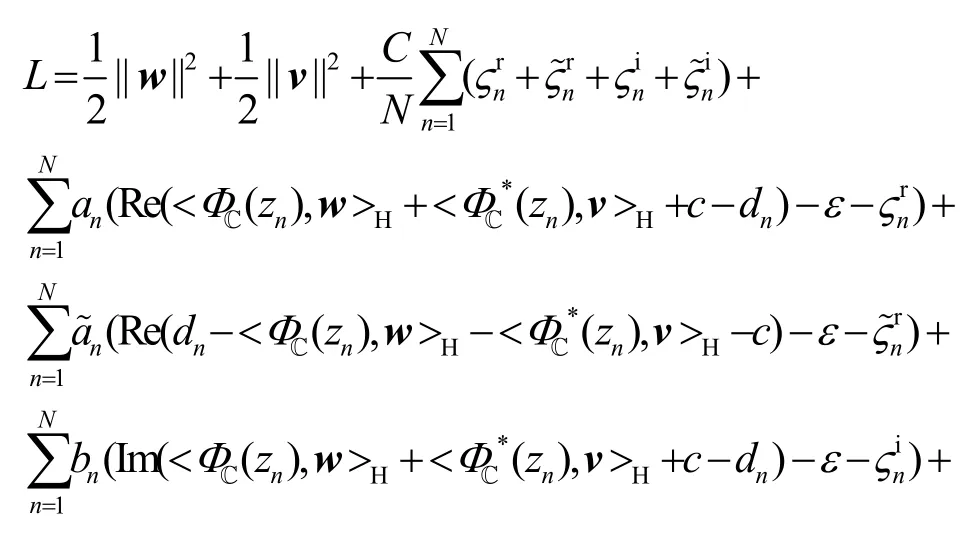
为利用鞍点条件，采用文献[16]的Wirtinger 微积分对复变量的共轭在复数希尔伯特空间内进行解析。

对于实变量，求解梯度的方法与传统方法一样。

在鞍点处，所有的梯度均应为零，故有

由式(10)可以看出，当诱导核选为实数核时，复数支持向量回归机可以等效为2 个支持向量回归机。用对偶因子(-an)表示的支持向量处理回归函数g(z)的实部，用对偶因子(-bn)表示的支持向量处理回归函数g(z)的虚部；当诱导核为复数核时，表示同时处理回归函数g(z)的实部和虚部。

当式(10)中的诱导核选为线性核时，g(z)建立的回归关系是线性的，对应的复数支持向量回归机的解为线性解；当诱导核选为非线性核时，g(z)表示的回归关系是非线性的，对应复数支持向量回归机的解为非线性解。通过不同诱导核的选择，可将线性解和非线性解统一在复数支持向量回归机的框架下。

复数支持向量回归机的求解过程与支持向量回归机的求解过程非常类似，不同之处在于，复数支持向量回归机采用广泛线性估计建立回归关系，求解鞍点时采用Wirtinger 微积分对复变量的共轭求导。此外，复数支持向量机用复数核的诱导核进行非线性映射。

4 算法描述

在支持向量回归机的框架下，对于线性信道的盲均衡，通过式(11)建立回归关系[10-14]。

其中，xn和yn分别表示均衡器的第n个输入信号和第n个输出信号；（n=1,2,…,N）；w表示均衡器的抽头系数向量。

处理非线性信道的盲均衡问题时，则需要采用核技巧[10]，通过式(12)建立回归关系。

其中，Φ(⋅)表示非线性映射函数。

由式(11)和式(12)可以看出，在支持向量回归机的框架下，解决线性信道和非线性信道的盲均衡问题需要分别建立不同的回归关系式。

而采用复数支持向量回归机处理盲均衡问题与支持向量回归机不同。在复数支持向量回归机的框架下，可通过广泛线性估计构造回归关系，如式(13)所示。

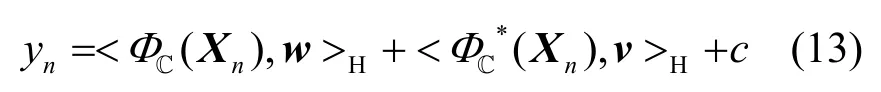
其中，w和v分别表示均衡器的2 个抽头系数向量，表示从均衡器输入信号向量空间Г到复数希尔伯特空间H 的特征映射。求解均衡器系数时，为避免优化过程中总是取得平凡解，取c=0。

为有效解决复数信号的盲均衡问题，构造代价函数如式(14)所示。

其中，ε-不敏感损失函数Lε定义如下。

将MMA 的误差函数代入式(15)，即令

其中，有

对式(14)的优化求解，可采用迭代重加权二次规划（IRWQP）方法[10]，考虑到IRWQP 的计算复杂度较高[11]，本文采用迭代重加权最小二乘（IRWLS）方法[17]求解，具体过程如下。

对式(14)做一阶泰勒展开，并取二次估计表示为

式(19)可以化简为

其中，有

CTE 是一个与变量无关的常数项。

式(20)是式(14)的二次估计式，在w=wk、v=vk处，且。因此，对代价函数J(w,v)定义一个下降方向，其中ws和vs是式(20)的最小二乘解（LS,least squares solution），并依该下降方向使用梯度下降搜索方法[17]求解式(14)的最小值，即

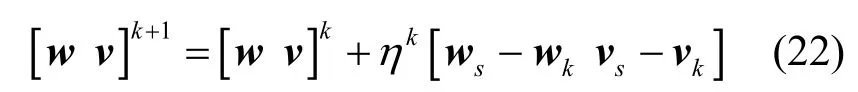
其中，ηk为步长，采用回溯搜索方法[19]迭代计算均衡器系数。

为求解ws和vs，应用Wirtinger 微积分，将式(20)分别对共轭变量w*和v*求解梯度向量。

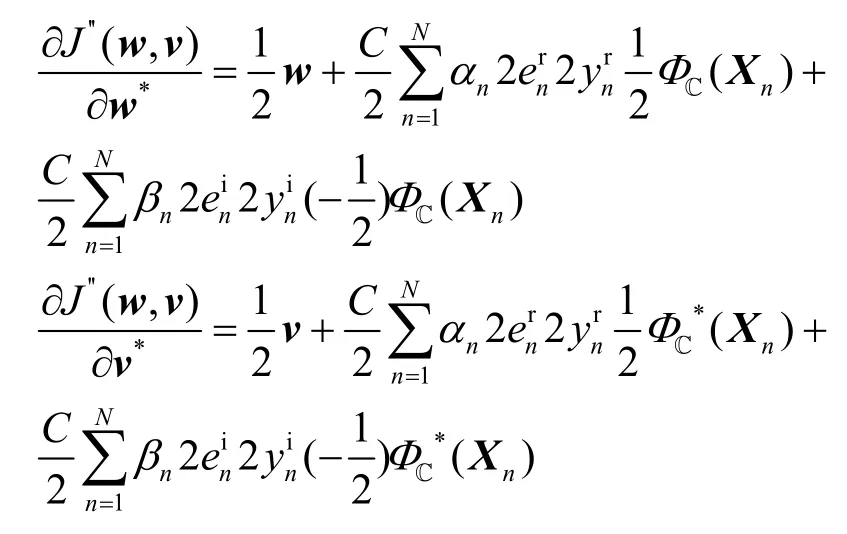
求得

将式(23)代入式(13)，得到式(24)。

将式(24)中复数希尔伯特空间内积用核函数进行替换，即令

得到均衡器第k个输出信号如式(26)所示。

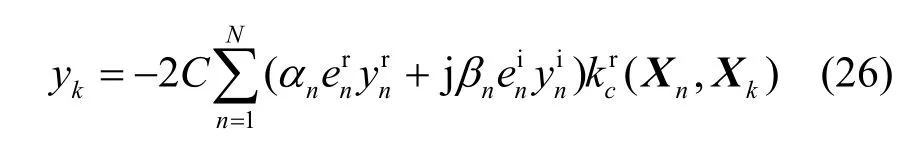
上述基于CSVR 框架，并采用迭代重加权最小二乘（IRWLS）法求解的盲均衡算法简称为CSVR-IRWLS，算法流程如下。

步骤1初始化w0，v0，选取核函数，用式(13)计算yn；用式(17)计算误差，式(21)计算系数αn、βn；令k=0，初始化ηk。

步骤2利用式(23)求解ws和vs。

步骤3利用式(22)更新wk+1、vk+1，如果J(wk+1,vk+1)＜J(wk,vk)，执行步骤5。

步骤4令ηk=ρηk,0＜ρ＜1，执行步骤3。

步骤5根据式(26)重新计算yn值，并重新计算误差及系数αn、βn，令k=k+1，返回步骤2，直到收敛。

由以上推导可知，本文提出的基于CSVR 的盲均衡算法采用式(13)建立统一的回归关系，并通过式(26)选择不同的线性或者非线性核函数，将线性信道和非线性信道的盲均衡问题统一在了一个框架下，均衡器的解形式相比支持向量回归机盲均衡算法更为简洁。

5 实验仿真分析

实验平台如下：CPU 为Intel(R)Core i7-7700 3.6 GHz，Windows10 64 bit，Matlab R2016a。

以输入QPSK 调制信号为例，添加零均值高斯白噪声。分别在线性信道和非线性信道下，仿真分析本文提出的CSVR-IRWLS 算法的性能，并与基于支持向量回归机的盲均衡算法进行性能比较。

CSVR-IRWLS 算法的收敛性能与CSVR 的惩罚因子C、不敏感损失因子ε，以及IRWLS 算法中的迭代步长η及其控制因子ρ的选取有着较强的关联性，上述参数的选取过程比较烦琐，一般可通过交叉验证方式[20]确定。表1 给出了CSVR-IRWLS 算法在不同输入序列长度时各参数的经验选取范围。

5.1 线性信道

在线性信道下，将CSVR-IRWLS 算法与文献[10]提出的基于IRWQP 的支持向量回归机算法（SVR-IRWQP）和文献[11,14]中基于IRWLS的支持向量回归机算法（SVR-IRWLS）进行对比分析。

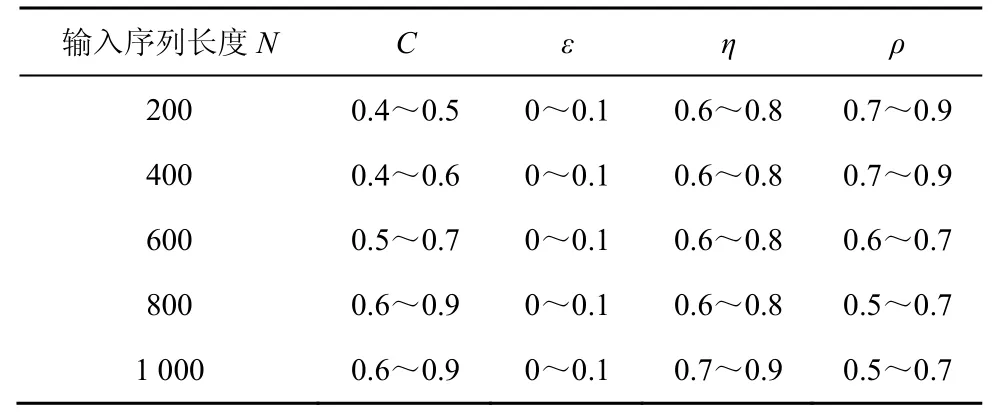
表1 CSVR-IRWLS 算法参数的选取

首先，考虑普通实数信道H1(z)=(0.4+z-1-0.7z-2+0.6z-3+0.3z-4-0.4z-5+0.1z-6)[10]，设置信噪比（SNR,signal noise ratio）SNR=25 dB，均衡器长度Lw=17，输入序列长度N=600。CSVR-IRWLS 算法中，初始化w0=Re(X0)，v0=Im(X0)，选取线性核函数（其中t=2），且取C=0.5、ε=0、ρ=0.7、η=0.6。SVR-IRWQP 算法参数的选取与文献[10]相同，SVR-IRWLS 算法参数的选取与文献[11,14]相同。为方便进行比较，以平均模值误差（AME,average modulus error）[10]来评价各算法的均衡性能，其计算式如式(27)所示。

图2 给出了H1(z)信道下3 种算法AME 值的收敛曲线。由图 2 可以看出，SVR-IRWQP 与SVR-IRWLS 算法在经过19 次迭代以后，AME 值收敛在-18 dB 左右。而本文提出的CSVR-IRWLS算法经过19 次迭代后的AME 值收敛在-27 dB 左右，相比SVR-IRWQP 与SVR-IRWLS 算法下降了大约9 dB。

其次，考虑普通复数信道，H2=[0.041 0+0.010 9j 0.049 5+0.012 3j 0.067 2+0.017 0j 0.091 9+0.023 5j 0.792 0+0.128 1j 0.396 0+0.087 1j 0.271 5+0.049 8j 0.229 1+0.041 4j 0.128 7+0.015 4j 0.103 2+0.011 9j]。CSVR-IRWLS 算法中，除取ρ=0.6 外，其他参数选取及初始化设置均与实数信道相同。SVR-IRWQP和SVR-IRWLS 算法参数的选取与实数信道相同，需要特别指出的是，此时的SVR-IRWQP 算法为实数化处理方式进行推导，详细过程可参阅文献[10]，此处不再赘述。

图2 实数信道H1(z)下3 种算法的AME 比较

图3 给出了H2(z)信道下3 种算法AME 值的收敛曲线。由图 3 可以看出，SVR-IRWLS 与SVR-IRWQP 算法在经过20 次迭代后，AME 值收敛在-28 dB 左右。而CSVR-IRWLS 算法经过25 次迭代以后，AME 值收敛在-42 dB 左右，相比SVR-IRWQP与SVR-IRWLS算法下降了大约13 dB。

图3 复数信道H2(z)下3 种算法的AME 比较

由图2 和图3 可以看出，在线性信道下，无论是实数信道，还是复数信道，由于SVR-IRWLS 与SVR-IRWQP 算法的初始化过程相同，因此初始的AME 值也相同。而本文提出的CSVR-IRWLS 算法初始化过程与以上2 种算法不同，AME 初始值略高。但是，随着迭代次数增加，CSVR-IRWLS 算法的AME 值迅速收敛，其最终收敛后的AME 值远远小于SVR-IRWLS 与SVR-IRWQP 算法，表现出更好的均衡性能。

为了客观地评价本文算法的性能，以获得一次输出所需的复乘次数作为计算代价的衡量标准[21]，表 2 给出了线性信道下，选用线性核函数的CSVR-IRWLS 算法与SVR-IRWQP 算法[10]以及SVR-IRWLS 算法[11,14]的计算复杂度。

表2 不同算法的复杂度比较

如表2 所示，由于实际均衡时输入序列长度N远大于均衡器长度Lw，因此，对于线性信道下复数信号的盲均衡，CSVR-IRWLS 算法的计算代价远低于文献[10]提出的SVR-IRWQP 算法的计算代价，但大于文献[11,14]提出的SVR-IRWLS 算法的计算代价，相比于支持向量回归机盲均衡算法，本文提出的基于复数支持向量回归机的盲均衡算法在较大程度提升均衡性能的同时，一定程度上增加了计算复杂度。

5.2 非线性信道

在非线性的三阶Volterra 信道模型[22]下进行CSVR-IRWLS 算法的仿真分析，并将其与采用核技巧[10]处理的文献[11,14]中的SVR-IRWLS 算法进行性能比较。均衡器抽头系数长度Lw=17。

5.2.1CSVR-IRWLS 算法核函数的选择

对于非线性信道的盲均衡，需选择合适的非线性核函数，如复高斯核，多项式核以及拉普拉斯核等。通常采用均方误差MSE 对算法的均衡性能进行评价，其计算式如式(28)所示。

设置信噪比SNR=25 dB，输入序列长度N=400，仿真分析CSVR-IRWLS 算法核函数的选择。实验中，分别选取复高斯核、多项式核以及拉普拉斯核并取C=0.5，ε=0，ρ=0.9，η=0.6 验证不同核函数对均衡性能的影响。

图4 给出了CSVR-IRWLS 算法选取3 种不同核函数时MSE 值的收敛曲线。由图4 可以看出，使用多项式核的CSVR-IRWLS 算法在经过大约25次迭代后收敛，收敛之后MSE 值在-12 dB 左右。使用复高斯核和拉普拉斯核的CSVR-IRWLS 算法收敛速度几乎相同，在经过大约18 次迭代后算法收敛，MSE 值稳定在-22 dB 左右。对比3 种不同核函数，基于复高斯核的CSVR-IRWLS 算法无论是收敛速度还是收敛后的均方误差值，其性能都是最好的。

图4 不同核函数对应MSE

图5 对比了基于复高斯核的CSVR-IRWLS 算法在不同SNR 下的误比特率（BER,bit error ratio）性能。由图5 可以看出，当N较小，如N=200 时，由于样本点较少，支持向量的数目不多，因此即使在SNR=30 dB 时，BER 值仍然高于0.01；当N增加到400 时，在SNR=25 dB 时的BER 值已低于0.001，在SNR=30 dB 的BER 值为0；观察N=600时的BER 曲线发现，当SNR 值低于10 dB 时，与N=400 时的BER 曲线没有明显区别，然而，当SNR值高于10 dB 以后，相同信噪比下，N=600 的BER值小于N=400 的BER 值。

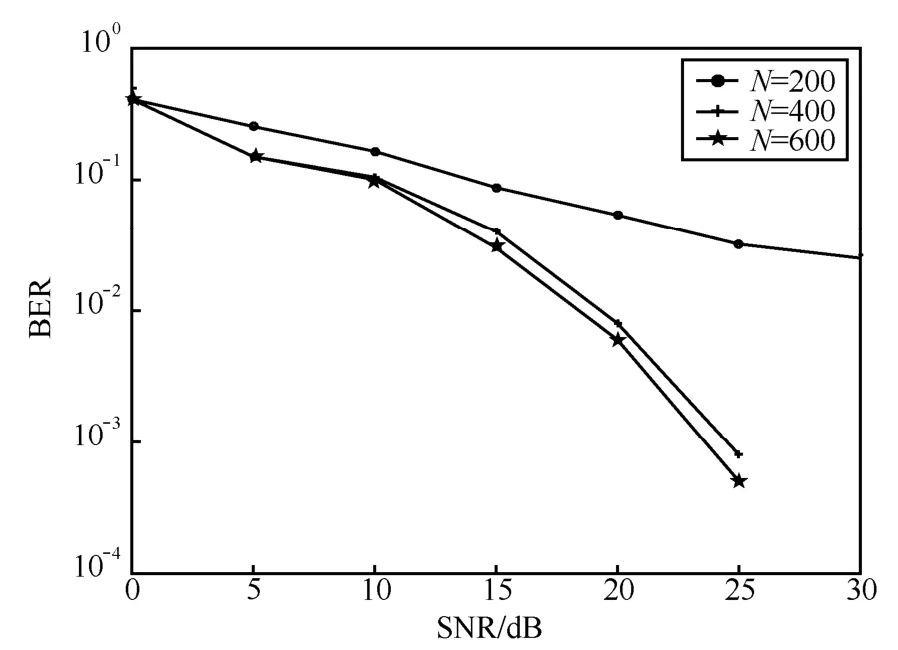
图5 不同样本点复高斯核BER

5.2.2CSVR-IRWLS 算法与SVR-IRWLS 算法的性能对比

本节通过实验对比分析了在非线性的三阶Volterra 信道模型下，CSVR-IRWLS 盲均衡算法与SVR-IRWLS 盲均衡算法的BER 性能。

取输入序列长度N=600。CSVR-IRWLS 算法中，选取复高斯核（核参数σ=2，t=1），C=0.5，ε=0，η=0.6，ρ=0.7。SVR-IRWLS 算法中，类似于文献[10]，选取高斯核（核参数σ=2）。2 种算法的BER 值随SNR 的变化曲线如图6 所示。

图6 非线性信道下不同算法的BER 性能

从图 6 可以看出，在相同信噪比下，CSVR-IRWLS 算法的BER 值总是低于SVR-IRWLS算法。当SNR=20 dB 时，CSVR-IRWLS 算法的BER值相比SVR-IRWLS 算法的BER 值减小了一个数量级；当SNR＞20 dB 时，CSVR-IRWLS 算法的BER值相比SVR-IRWLS 算法的BER 值的减小更为明显，如SNR=30 dB 时，SVR-IRWLS 算法的BER值为0.01，而CSVR-IRWLS 算法的BER 值已为0。由此可以得出结论，在非线性信道下，对于复数信号的盲均衡，本文提出的CSVR-IRWLS 算法表现出更低的误码率性能。

进一步比较本文提出的CSVR-IRWLS 算法（选取复高斯核）和文献[11,14]的SVR-IRWLS 算法（选取高斯核）的计算复杂度，结果如表4 所示。

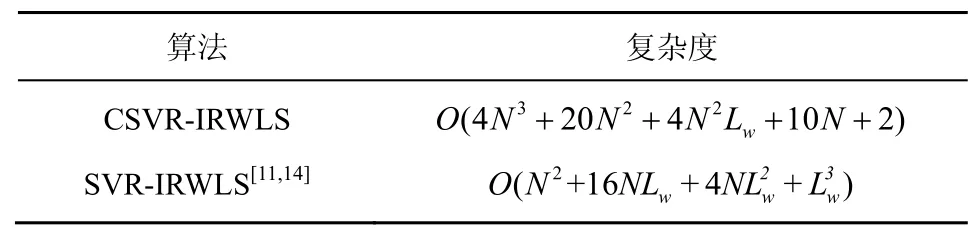
表4 CSVR-IRWLS（复高斯核）算法与SVR-IRWLS（高斯核）算法的复杂度比较

由表4 可知，对于非线性信道下的复数信号盲均衡，由于N＞＞Lw，CSVR-IRWLS 算法的计算代价大于文献[11,14]中的SVR-IRWLS 算法的计算代价，但在相同信噪比的情况下，其均衡的误码率相比SVR-IRWLS 算法可降低一个数量级以上。

6 结束语

本文提出了一种基于复数支持向量回归机的盲均衡算法CSVR-IRWLS，该算法将MMA 的误差函数代入CSVR 的惩罚项构造代价函数，利用Wirtinger 微积分求解鞍点，在复数希尔伯特空间直接对复数信号进行解析，以迭代重加权最小二乘方式寻找最优解，将线性信道和非线性信道的盲均衡问题统一在了一个框架下。针对QPSK 调制信号的仿真实验结果表明，无论是在线性信道还是非线性信道下，相比于基于支持向量回归机的盲均衡算法，本文算法的均衡性能均得到了明显提升。然而，由于采用带核函数的复数支持向量回归框架构造代价函数，并采用广泛线性估计建立回归关系，相比基于支持向量回归机的SVR-IRWLS 算法，本文算法的复杂度较高，接下来的工作需要进一步研究复数支持向量回归机框架下盲均衡器代价函数的快速优化求解方法。