基于能效的渐近式RZF 协作波束成形算法研究

张颖慧，张彪，逯效亭，刘洋

（内蒙古大学电子信息工程学院，内蒙古 呼和浩特 010021）

1 引言

多输入多输出（MIMO,multi-input multi-output）技术广泛应用于无线通信系统中，通过部署多个天线可以提高无线链路的可靠性并实现具有更高频谱效率的无线通信网络[1-2]。由于Massive MIMO 技术具有突出的理论优势，包含许多低功率天线的Massive MIMO 系统成为现代通信发展的未来趋势，引起学术界和工业界的极大关注[3]。Massive MIMO 系统配备数百根天线，理论上可以在无线信道上支持非常高的数据速率而不需要额外的带宽和传输功率。然而，在获得更好性能的同时，大量的天线在各种设计中也引入了更高的计算复杂度[4-5]，如波束成形设计、信号检测和信道估计。通过使用准确的信道状态信息（CSI,channel state information），波束成形算法可以显著提高Massive MIMO 系统性能[6-7]，但普遍存在复杂度过高而无法实际应用的问题。正则化迫零（RZF,regularized zero-forcing）[8-9]波束成形可以控制每个用户引入的干扰量并且在性能和复杂度之间做出良好的权衡，特别适合于Massive MIMO 系统。目前，在关于天线发射功率约束的研究中，天线发射功率约束值均为其上限，每根天线的功率约束值均相同且固定[10-11]。近些年，低复杂度非迭代的多流 RZF（Multiflow-RZF）波束成形的相关研究已经取得了相应的进展[12-15]。文献[12]研究了Multiflow-RZF波束成形算法，考虑了波束成形的正则化项中天线发射功率约束的影响。文献[13]介绍了基于Multiflow-RZF 波束成形的Max-SLNR 设计方案，所提方案表明 Multiflow-RZF 波束成形设计在Massive MIMO 系统中具有较低复杂度和近似最优性能。文献[14]研究了异构网能效优化问题，利用Multiflow-RZF 波束成形设计，将能效（EE,energy efficiency）优化问题转换为最优功率分配问题，具有复杂度低并且与天线数量无关的优点。文献[15]研究了基于Multiflow-RZF 波束成形设计不同部署场景下的异构小基站部署方案。上述文献在设计Multiflow-RZF 波束成形时，只是简单地将正则化项中的每根天线功率约束值均设为固定的上限值，而忽略了在实际部署环境中天线数量、用户数和服务质量（QoS,quality of service）等因素的影响，由此设计的Multiflow-RZF 波束成形并不是最佳波束成形。由于无线通信系统中每根天线都有自己的功率放大器，即每根天线均可以分配发射功率，因此对每根天线进行合理约束与EE 优化在实际部署环境中更有价值。在每根天线功率的约束下，利用凸优化等数值方法，例如半正定规划（SDP,semi-definite programming）、二阶锥规划（SOCP,second order cone programming）来获得最优解[11,16]。

Massive MIMO 技术在大幅提高无线链路容量的同时增加了用户之间的干扰，从而影响用户QoS和系统EE。为此，协作多点（CoMP,coordinated multipoint）传输技术应运而生[17-18]。在异构Massive MIMO 中，宏基站和小基站之间通过CoMP 传输技术可以有效抑制干扰并提高无线资源的利用率，对改善系统EE 起着重要作用。目前的相关研究主要集中在最大化EE 或频效（SE,spectrum efficiency）的传输功率优化上，而未考虑回程功耗的影响[19-20]。然而，在实际部署环境中，回程功耗不能忽略，特别是在多点协作的多用户Massive MIMO 场景中，回程功耗将会成为限制基站协作性能的重要影响因素。然而，CoMP 传输技术也会带来更高的复杂性和同步需求、更多的信道估计和开销等问题[21]，特别是回程功耗开销[22-23]。在实际部署环境中，CoMP的传输性能在很大程度上取决于回程网络的性能。CoMP 传输不可避免地要将每一个请求内容复制到每一个参与协作的基站中，这将导致回程链路的功率消耗剧增。最近，回程功耗对系统功耗的影响引起了极大关注[24-26]。此外，回程功耗对系统总功耗的影响与回程本身的拓扑结构[13]有关，并且不同的拓扑结构也会有不同类型的回程功耗模型[27]，回程拓扑结构将会对系统性能产生重要影响。文献[22,27-28]研究了异构网中不同回程拓扑结构下的系统SE 和EE 优化，研究表明选取合适的回程拓扑结构，有利于提高系统整体性能。本文考虑光纤和无线2 种回程拓扑结构，并将2 种回程结构进行结合，应用到异构Massive MIMO 系统中。

Massive MIMO 技术能够显著提高无线接入系统的信道容量、频谱效率、能量效率等，通过在大量天线上传输信号，Massive MIMO 技术可以实现非常高的性能增益。然而，天线数量的增加也带来了信道状态信息反馈规模大、波束成形设计复杂等问题。适合Massive MIMO 系统下波束成形的算法设计，是改善系统EE 性能的关键。本文研究了下行异构Massive MIMO 系统EE 优化问题，提出一种基于EE 的低复杂度渐近式RZF 协作波束成形（ARZF-CoBF,asymptotic regularized zero-forcing coordinated beamforming）算法。首先，构建了考虑回程功耗的系统模型，提高了算法的实用性。对比不同天线数和不同QoS 对系统功耗的影响，研究满足QoS 约束和天线发射功率约束下的功率优化问题。其次，研究了满足QoS 约束和天线功率约束，基于节能的蜂窝网络与小小区结合的功率分配优化问题。最后，将优化问题转换为采用渐近式联动优化Multiflow-RZF 波束成形设计的功率分配问题，通过凸优化的方法对天线功率约束集合做最优选择，渐近地获得最优波束成形设计以平衡用户间的干扰，实现异构Massive MIMO 系统协作EE 最优。

2 系统模型

考虑一个下行双层异构网中单小区模型，在第一层部署宏基站，且每个宏基站配备NBS根天线。第二层随机均匀部署S个小基站，每一个小基站均配备NS根天线。宏基站和小基站具有不同的最大天线发射功率，分别为q0和qs，q0＞qs，qs表示发射功率约束值。K个用户随机均匀部署在异构网中，用户数不小于宏小区内基站个数，每个小小区内至少有一个用户。则第k个用户接收到的信号为

其中，C表示参与协作的小基站数；hj,k表示第j个基站到第k个用户的信道，，,j∈{1,2,…,S}表示小基站的索引值，而j=0则表示宏基站的索引值，且假设信道服从均值为0、方差为1 的复高斯分布；Pj,k表示第j个基站对第k个用户的传输功率；宏基站以及第j个小基站发送给第k个用户的信号分别表示为s0,k和sj,k，且满足均值为0，方差为1，均为单位归一化向量，分别表示来自宏基站和小基站发送信号的波束成形方向向量；为高斯白噪声。

基站之间进行协作波束成形，每一个用户可以被多个基站服务，这意味着用户可以同时接收到来自宏基站与小基站发送的信号，即用户将收到多流信号。则第k个用户的信干噪比（SINR,signal to interference plus noise ratio）可以表示为

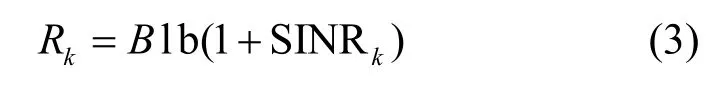
其中，B表示带宽。

如图1 所示，在双层异构网中，部署一个宏基站和S个小基站，并随机均匀部署K个单天线用户。

图1 双层回程异构网

将系统的功耗定义为传输功耗Pt与基站固有消耗Pc之和[29]，即Ptotal=Pt+Pc。Pc正比于天线数目[12]，可以表示为

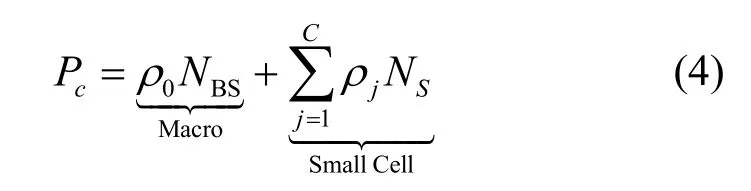
传输功耗为

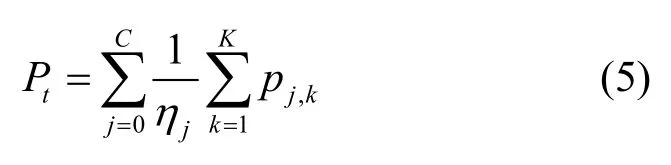
其中，η0和ηj分别表示宏基站和第j个小基站的功率放大器效率，Pj,k表示第j个基站对第k个用户的传输功率。文献[30]给出了异构网中不同基站类型的功耗模型，但没有考虑回程功耗。由于所有的CoMP 用户的协作信息都需要在参与协作的基站之间共享[31]，导致严重的回程功率损耗。因此，异构网中CoMP 场景考虑EE 是非常必要的。本文将考虑回程功耗对异构网部署的影响[26]，对已有模型进行借鉴并优化。在考虑回程功耗的情况下，系统功耗模型可以重新定义为

其中，PBH表示回程功耗。

本文考虑了2 种回程部署方式，分别为光纤回程和无线回程，并将这2 种回程部署方式结合在一起。宏基站通过光纤回程连接到核心网络，而小基站则通过无线回程连接到核心网络，如图1 所示。回程功耗可以表示为

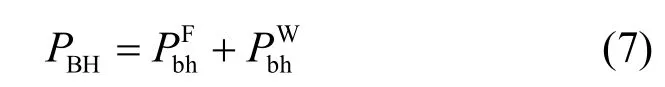
其中，maxdl表示汇聚节点交换机（sink switch）允许的最大下行链路接口数目，表示基于光纤的汇聚交换机产生的最大功耗，Nul表示聚合交换机处收集的流量与上行链路接口最大传输速率Umax的比值，即

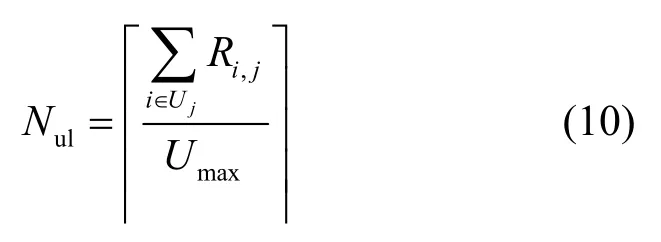
其中，Uj表示由第j个基站服务的用户合集，Uj⊂{1,2,3,…,K}；i∈Uj表示第j个基站已知第i个用户的数据信息并且向该用户传输此信息，在异构网中，部分用户可以由多个基站联合服务，也可由单个基站服务；Ri,j表示基站j对用户i提供的数据传输速率，即

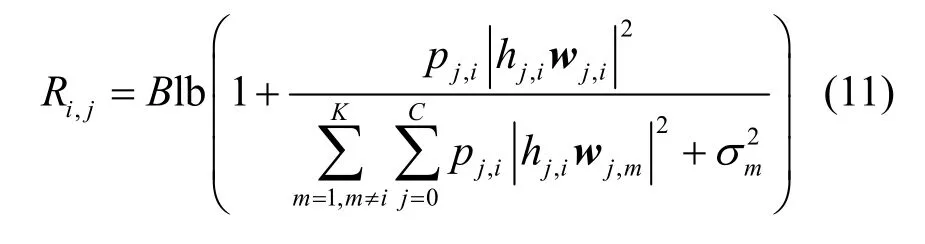
无线回程功耗可以表示为

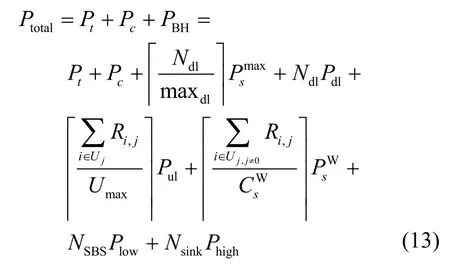
本文将EE 定义为单位时间内吞吐量（单位为bit/s）与系统总功率消耗（单位为W）的比值。为使仿真结果更加准确，小区内用户位置以及信道均随机生成，并对算法进行多次实验最终得到统计平均值，使仿真结果更接近实际情况。

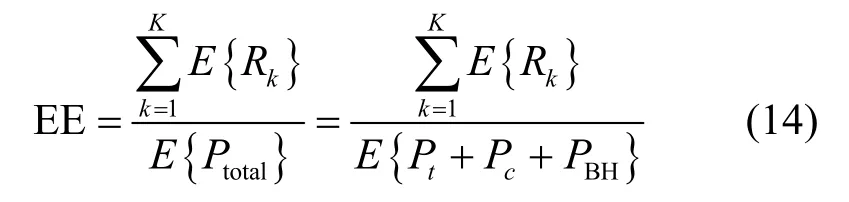
3 渐近式RZF 协作波束成形算法

本文关注异构Massive MIMO 系统中的功率约束合理设置方案。与目标函数是最小化总功率的传统功率分配方案不同，本文考虑在满足QoS 约束和天线功率约束条件下的系统EE 优化问题。本文将QoS 定义为信息率，单位为bit·(s·Hz)-1，QoS 约束条件为SINRk≥γk,∀k，其中，γk为目标SINR 阈值，满足。因此，本文将异构网的EE最优化问题表示为满足基站天线功率和用户SI NR大于最低目标SINR 阈值的约束条件时的最小化总功耗，即

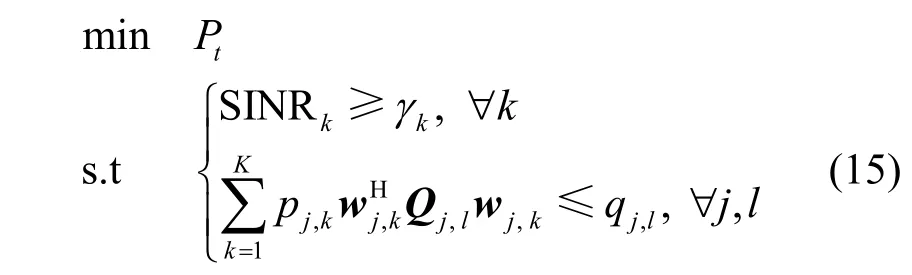
其中，γk表示第k个用户的目标SINR；Qj,l表示权重矩阵，,j=1,…,S；表示第l根天线对第k个用户的传输功率；qj,l表示第j个基站中的第l根天线的最大发射功率。进行优化时，基站每根天线传输功率不超过其最大发射功率，每个服务用户最低信息率为Blb(1+γk)，实现系统EE 优化。

本文将EE 最优波束成形设计问题转换为功率分配最优问题，使用Multiflow-RZF 波束成形将优化式(15)转换为式(16)，优化变量pj,k与天线的数量无关。

其中，pj,k表示异构网中第j个基站对第k个用户分配的功率，qj,l表示第j个基站中的第l根的天线功率约束。文献[12]研究了一种低复杂度的非迭代的Multiflow-RZF 波束成形算法，Multiflow-RZF 波束成形的正则化项中考虑了天线发射功率约束的影响。研究表明 Multiflow-RZF 波束成形设计在 Massive MIMO 系统中具有较低复杂度和近似最优性能[12]。Multiflow-RZF 波束成形矩阵表示为

当系统中既存在加性白噪声又存在其他干扰时，可以通过调节α来平衡噪声与干扰。正则化项中qj集合中的任意一个qj,l(qj,l∈qj)值均相同，每根天线的功率约束值qj,l均为其允许的最大天线发射功率qmax(qj,l≤qmax)。qj,l用来构造Multiflow-RZF 波束成形并在式(16)中作为天线发射功率的固定的约束值条件。本文对所有基站的天线功率约束集合q(qj,l∈qj⊂q)进行改进，动态适应天线数、用户数、服务质量等因素的变化，通过最优化集合q选择优化波束成形。本文通过在α中对功率约束集合q乘以修正系数集合β，，其中βj,l∈β j⊂β，0＜βj,l≤ 1，则表示第j个基站中的第l根天线的发射功率约束修正值，βj,l qj,l取值范围为(0,qmax]。修正后Multiflow-RZF 波束成形矩阵为

通过对集合q乘以修正系数集合β，基站的每一根天线获得最佳功率约束，在优化功率分配的同时，联动优化Multiflow-RZF 波束成形，渐进地获得最优波束成形设计，最终实现系统EE 最优。式(16)可以进一步优化为式(19)。式(19)在满足功率非负性条件、QoS 约束条件、天线功率约束条件和最佳天线功率约束修正系数条件的情况下，使系统功耗最小。

根据以上分析，在给定目标用户的SINR 和天线最大传输功率约束值的条件下，优化式(19)可由ARZF-CoBF 算法求解。该算法使用了CVX 凸优化工具包求解最优功率分配P*。在此优化算法下，基站各天线的传输功率不超过其最佳发射功率约束q*，并且可以保证每一个用户获得一个最低基站服务质量的同时最小化系统总功耗。在传统异构Massive MIMO 系统能效研究中，采用经典的松弛凸半正定规划波束成形算法[12]，可以在多项式时间内找到最优解，但在Massive MIMO 系统中，其复杂度也随着天线数的增加而急剧增大。松弛凸半正定规划波束成形算法复杂度为O(N2)，N为天线数，在Massive MIMO 系统中可以达到上百根，算法不适用于Massive MIMO 系统。本文提出的ARZF-CoBF 算法具有较低的复杂度，其复杂度只与系统中的基站数和用户数有关而与天线数无关，算法可以在优化功率的同时保持相对较低的复杂度，其复杂度为O(K t Kr)，Kt为基站数，Kr为用户数。与经典的松弛半正定规划波束成形算法相比，ARZF-CoBF 在Massive MIMO 系统中具有较低的复杂度，可实现近似最优性能。ARZF-CoBF算法如算法1 所示。

算法1ARZF-CoBF 算法

步骤1初始化修正系数β（βj,l=1,∀j,l）、天线功率约束集合q、信道H，初始化系统总功耗Ptotal=0 。

步骤 2计算当前天线功率约束集合q下Multiflow-RZF 波束成形矩阵W。

步骤3由步骤2)得到的W和H，利用CVX凸优化工具计算优化式(19)，优化满足当前约束条件下的分配功率P*和优化后的β，并计算当前总功耗，得到优化后的天线功率约束集合qtmp=qβ。

步骤4更新天线功率约束集合q=qtmp。重复步骤2 和步骤3，得到更新q后的当前总功耗Ptmp，并判断Ptmp是否小于上一步得到的总功耗Ptotal，不满足条件时重复步骤2 和步骤3，直到Ptmp为最小值，得到最佳天线功率约束q*限定下系统总功耗Ptotal=Ptmp、最佳功率分配p*、W和H。

步骤5根据步骤1～步骤4 得到的q*、p*、W和H，计算系统吞吐量和EE。

4 仿真结果及分析

本文构建了异构Massive MIMO 系统模型，参照LTE-A 标准，设置仿真参数。考虑回程功耗、基站天线数、协作基站数、QoS 和用户数因素对系统EE 的影响，对ARZF-CoBF 算法进行仿真。

4.1 仿真场景

仿真场景为一个双层异构正六边形单小区，NSBS个家庭基站在距离小区中心350 m 处，按角度划分，均匀部署在小区内，小基站之间最小间距为40 m。协作小基站数NCBS∈{0,2,4}，其中，NCBS=0表示异构网内只有宏基站且没有协作小基站。小区内随机部署K个用户，则小区内的用户存在以下3种情况。

2)用户只由第j个小基站服务（如并且

如图2 所示，系统中的用户可以被单基站服务也可以被多基站联合服务。当宏基站在不超过其天线功率约束的情况下，不能为边缘用户提供最低QoS 时，宏基站可联合小基站共同服务该用户，或者该用户只由与其距离较近的小基站独立提供服务以平衡宏基站负载。

图2 协作方案

本文假设信道为瑞利衰落模型，路径损耗模型为非视距（NLoS,non-line of sight）模型，仿真参数如表1 所示。

表1 仿真参数

4.2 仿真结果

部署宏基站和NCBS个小基站组成下行双层异构网。系统共部署K个用户，随机均匀分布在异构网内。在异构网CoMP 场景中，本文将系统功耗定义为传输功耗、电路功耗和回程功耗之和，考虑同时满足QoS 约束和功率约束的双层异构网的EE 问题。基于快速收敛、低复杂度的Multiflow-RZF 波束成形算法，对功率约束q集合做最优选择，渐进地获得最优波束成形设计以优化功率分配，提出性能更好的 ARZF-CoBF 算法，进一步提高异构Massive MIMO 系统的EE。

图3 给出了不同宏基站天线数和协作小基站个数的系统功耗，并比较了有回程和无回程2 种系统功耗场景。在无回程功耗场景中，当宏基站天线数较小时，系统功耗较高，随着天线数的增加，基站之间做协作波束成形，系统功耗将呈现减小的趋势。由于系统电路功耗与天线数成正比[33]，更多的天线数会带来更多的电路功耗，随着天线数的大大增加，电路功耗将与传输功耗相当甚至会占据主导地位。因此，系统功耗将会随着天线数的增加而呈现先减小后增加的趋势。有回程功耗的场景与之类似。同时，基站通过CoMP 传输技术服务用户的方式和增加协作小基站个数，可以进一步降低系统功耗，但回程功耗也会随着协作小基站数的增加而增加。此外，在给定用户数和QoS 的情况下，2 种场景下的功耗之间的差距趋于稳定。

图4 给出了不同QoS 和协作小基站个数的系统功耗，并比较了有回程功耗和无回程功耗的2 种系统功耗场景。从图4 可以看出，随着QoS 的增加，系统将需要分配更多的资源（如传输功耗）以服务用户，系统总功耗将会随着QoS 的增加而快速上升。在给定天线数的情况下，电路功耗变化将趋于稳定，而传输功耗随QoS 的增加变化明显。增加协作基站数有利于降低系统总功耗，但更多协作基站也意味着需要更大的回程开销，回程功耗也会逐渐增大。此外，在用户数以及天线数固定的情况下，随着QoS 的增加，系统总功耗中传输功耗将占据主导地位，2 种场景下的功耗之间的差距逐渐减小。

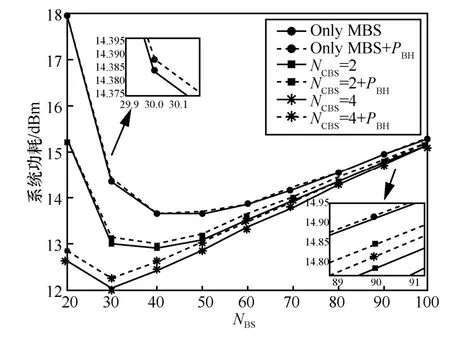
图3 考虑回程功耗时不同天线数下的系统功耗（NCBS∈{0,2,4}，NBS∈{20,30,…,100}，QoS=1 bit·(s·Hz)-1，N S=2）

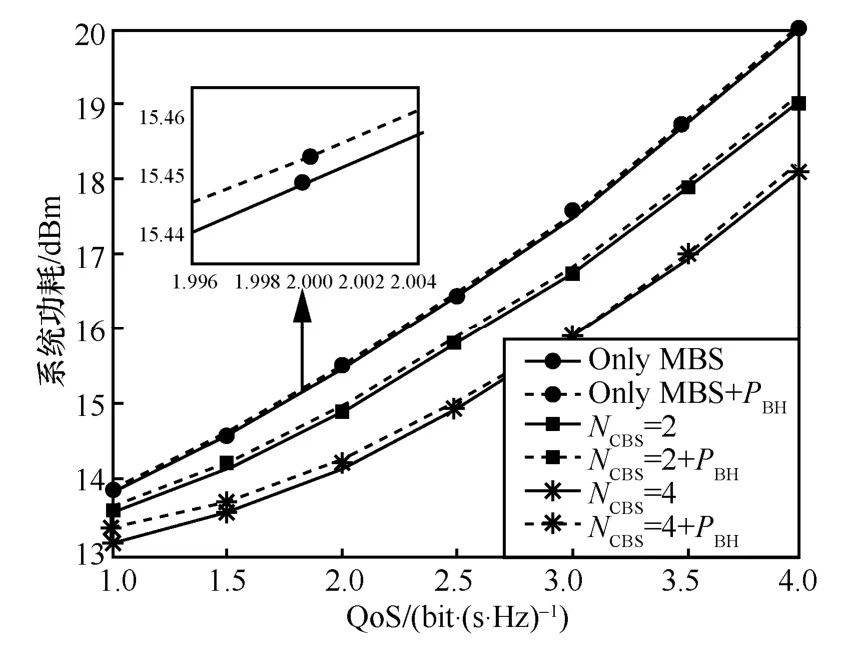
图4 考虑回程功耗时不同QoS 下的系统功耗（NCBS∈{0,2,4}，NBS=64，N S=2）

CoMP 和异构网是在未来无线蜂窝网络中实现高EE 和改善覆盖率的2 个有效的概念。为了满足移动数据业务几乎呈指数性的增长需求，需要部署大量低功率小基站以及诸如无线远端射频单元（RRH,remote radio head）的远程天线元件，因此，可以推断出用于回程链路上的开销将大大增加，不可忽视。由图3 和图4 可知，在异构Massive MIMO 场景中利用CoMP 传输技术来提高系统EE 时，回程功耗是限制基站协作性能的重要因素之一，设计系统EE 优化时必须考虑这一因素。

图5 比较了不同协作基站数和不同天线数下基于Multiflow-RZF 和基于ARZF-CoBF 这2 种算法的EE。由图5 可以看出，由于电路功耗限制的影响，系统EE 曲线呈现先增加后减小的趋势。在天线数较低时，与 Multiflow-RZF 算法相比，ARZF-CoBF 算法的系统EE 大幅提高。图5(a)中，当NBS=30，NCBS=4 时，ARZF-CoBF 算法EE值比Multiflow-RZF 算法EE 值提高了36.8%。同时，随着协作基站数的增加，ARZF-CoBF 算法EE 提高幅度也在增加。当天线数较高时，ARZF-CoBF 算法EE 高于Multiflow-RZF 算法。因此，ARZF-CoBF 算法EE 比Multiflow-RZF 算法更接近最优值。与图5(a)相比，图5(b)通过增加小基站天线个数，ARZF-CoBF 算法的系统EE得到进一步的提高。

图5 不同宏基站天线数下的系统能效（NCBS∈{0,2,4},NBS∈{20,30,…,100},QoS=1bit ⋅ (s ⋅Hz)-1）

在不同QoS 约束下，当NS=2，NCBS∈{0,2,4}和NBS∈{64,128}时的系统EE 如图6 所示。仿真结果表明，随着QoS 的增加，系统EE 呈现先增加后减小的趋势，即在给定天线数的情况下，系统可以为用户提供一个最佳的服务质量同时保证系统EE 最高。与此同时，ARZF-CoBF 算法EE值相对于Multiflow-RZF 算法EE 值的提高幅度也随着 QoS 的增加而增加。当 QoS 较低时，ARZF-CoBF 算法EE 与Multiflow-RZF 算法接近，但仍高于Multiflow-RZF 算法。如图6(a)所示，当QoS=1、NCBS=4 时，ARZF-CoBF 算法EE 比Multiflow-RZF 算法提高了1.7%；当QoS=2.5、NCBS=4时，ARZF-CoBF 算法EE 比Multiflow-RZF 算法提高了1.9%。同时，增加协作基站数也可以进一步提高ARZF-CoBF 算法性能。从图6(b)可以看出，在系统EE 相同情况下，更多的天线数可以为用户提供更高的服务质量，同时天线数较多时，ARZF-CoBF 算法EE 和Multiflow-RZF算法接近。

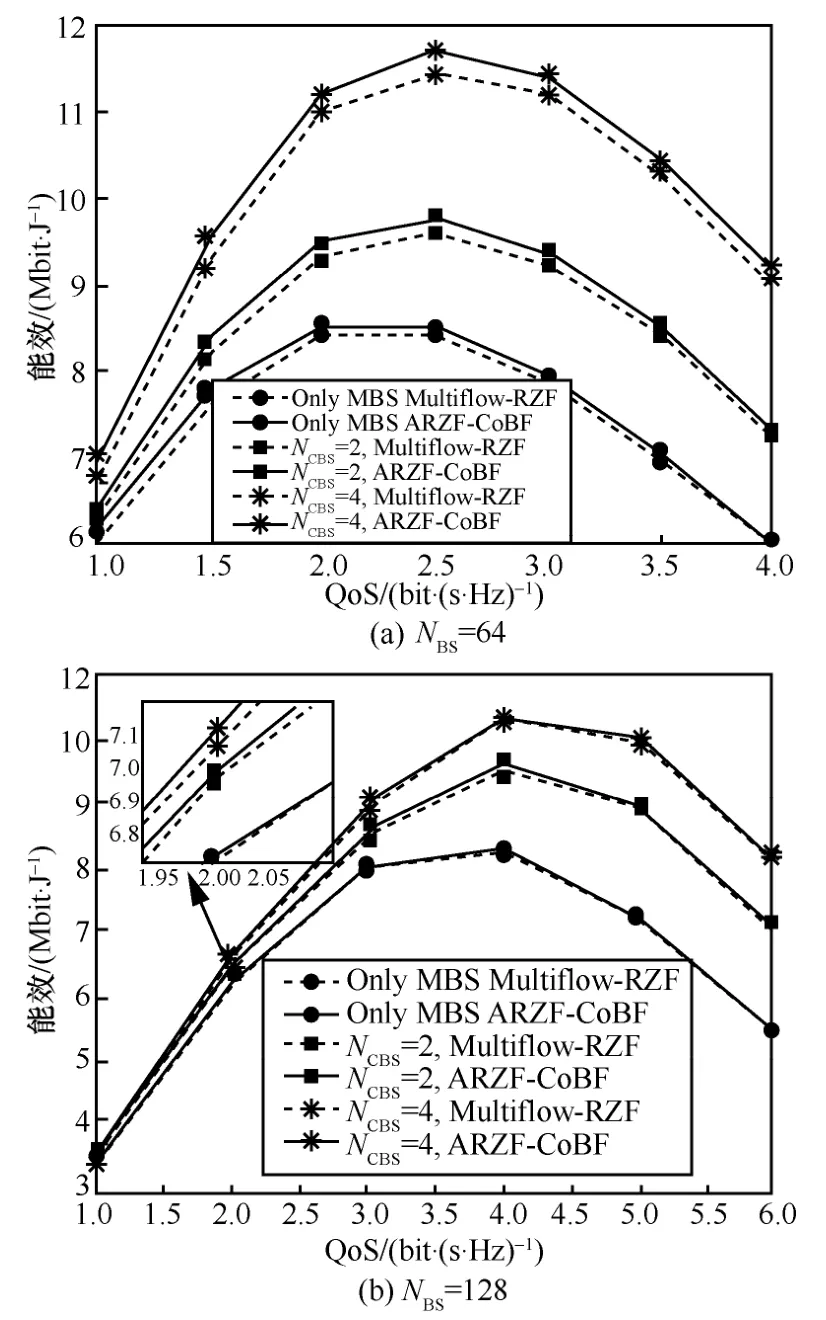
图6 不同QoS 下的系统能效（NCBS∈{0,2,4},NS=2）

图7 给出了用户数和协作基站数这2 种因素对系统EE 的影响。从图7 可以看出，在基站天线数一定的情况下，系统可以服务的用户数量存在一个临界值，即存在一个最佳服务用户数量，在该用户数下，系统可以保证每一用户的最低服务质量要求。同时还发现，在相同用户数和宏基站天线数的情况下，通过增加部署小基站个数、基站协作的方式也可以提高系统的EE。从图7(a)中可以看出，在天线数和QoS 一定的情况下，ARZF-CoBF 的EE与Multiflow-RZF 的EE 随用户数量的增加而算法性能下降。随着用户数增多时，ARZF-CoBF 算法EE 和Multiflow-RZF 算法性能下降。从图7(b)中可以看出，在相同用户数和协作小基站数的情况下，通过增加宏基站天线个数，可以实现更高的系统EE。

图7 不同用户数量下的系统能效（NCBS∈{0,2,4},QoS=1 bit·(s·Hz)-1）

5 结束语

本文充分考虑异构网CoMP 场景中的回程功耗影响，考虑更符合Massive MIMO 实际应用的回程功耗系统模型，提出了一种基于EE 的低复杂度渐近式RZF 协作波束成形算法。本文提出的算法解决了多流正则化迫零波束成形算法将正则化项中的每根天线功率约束值均设为固定的上限值，设计的Multiflow-RZF 波束成形并不能获得最佳EE的问题。本文提出的算法还重点研究了满足QoS约束和最优天线功率约束的蜂窝网与小小区结合的节能优化，解决了现有相关研究忽略在实际部署环境中天线数量、用户数和QoS 等因素影响的弊端，比较了不同协作基站数量、天线数量、用户数和QoS 下的协作EE，提出了基于EE 的ARZF-CoBF 新算法。本文结论可以根据不同的系统情况和服务要求，选择适当的基站协作方案及参数，以获得EE 最优的系统设计方案。因此，本文内容对异构Massive MIMO 系统设计具有重要的指导意义。