非均相复合驱非连续相渗流特征及提高驱油效率机制

2019-11-02吴德君曹绪龙郭兰磊

中国石油大学学报（自然科学版） 2019年5期

侯健, 吴德君, 韦贝, 周康, 巩亮, 曹绪龙, 郭兰磊

(1.非常规油气开发教育部重点实验室(中国石油大学(华东)),山东青岛 266580; 2.中国石油大学(华东)石油工程学院,山东青岛 266580; 3.中国石油大学(华东)新能源学院,山东青岛 266580; 4.中国石化胜利油田分公司,山东东营 257015; 5.中国石化胜利油田分公司勘探开发研究院,山东东营 257015)

聚合物驱后油藏仍有约一半或以上的原油滞留在地下未被采出,须进一步探索新的提高采收率方法[1]。与水驱相比,聚合物驱后油藏开发面临着更大的难题:一是储层非均质更严重,注入流体易窜流;二是可动剩余油更分散,原油采出困难,现有驱油体系难以采出。针对以上问题,在驱油介质中引入可变形运移的“软固体”凝胶颗粒,与聚合物和表面活性剂溶液互配加大调驱力度,构建起非均相复合驱油体系,达到大幅度提高聚合物驱后油藏采收率的效果[2]。目前,非均相复合驱技术已在胜利油田得到推广应用[3-4],在孤岛、孤东及胜坨等特高含水主力油田共推广单元17个,提高采收率8.3%,增油降水效果显著。由于凝胶颗粒的加入,非均相复合驱过程表现为非连续相流动。驱油体系中由于聚合物和表面活性剂的存在,渗流还具有非牛顿流体流动、油水界面张力降低、润湿性改变等特性。笔者采用微流控及双管岩心流动实验揭示非均相复合驱非连续相渗流特征,综合考虑凝胶颗粒、聚合物及表面活性剂等特性,建立非均相复合驱微观渗流格子玻尔兹曼模拟方法,阐释非均相复合驱提高驱油效率机制,为非均相复合驱大幅度提高采收率提供理论支持。

1 非连续相渗流特征

非均相复合驱油体系中包含连续相(含水、聚合物、表面活性剂等组分)和非连续相(凝胶颗粒)。凝胶颗粒吸水膨胀后成为可变形的“软固体”,在渗流过程中运移至孔隙喉道可产生堵塞,随着喉道两端压差增大,颗粒能变形通过喉道,继续向深部运移。凝胶颗粒运移、滞留堵塞、变形通过、再运移的渗流现象,使非均相复合驱流动表现出非连续相渗流特征。

1.1 微流控实验

建立凝胶颗粒悬浮液微观渗流实验系统,其中微流体进样系统通过外接钢瓶洁净气体作为压力输出源,依次经过精密调压阀、气压控制泵、储液瓶以及精度流量控制阀,最后连接芯片传感器以控制驱替压力。实验可施加压力为0～0.7 MPa,微通道喉道长度为300 μm,宽度为24 μm, 如图1所示。

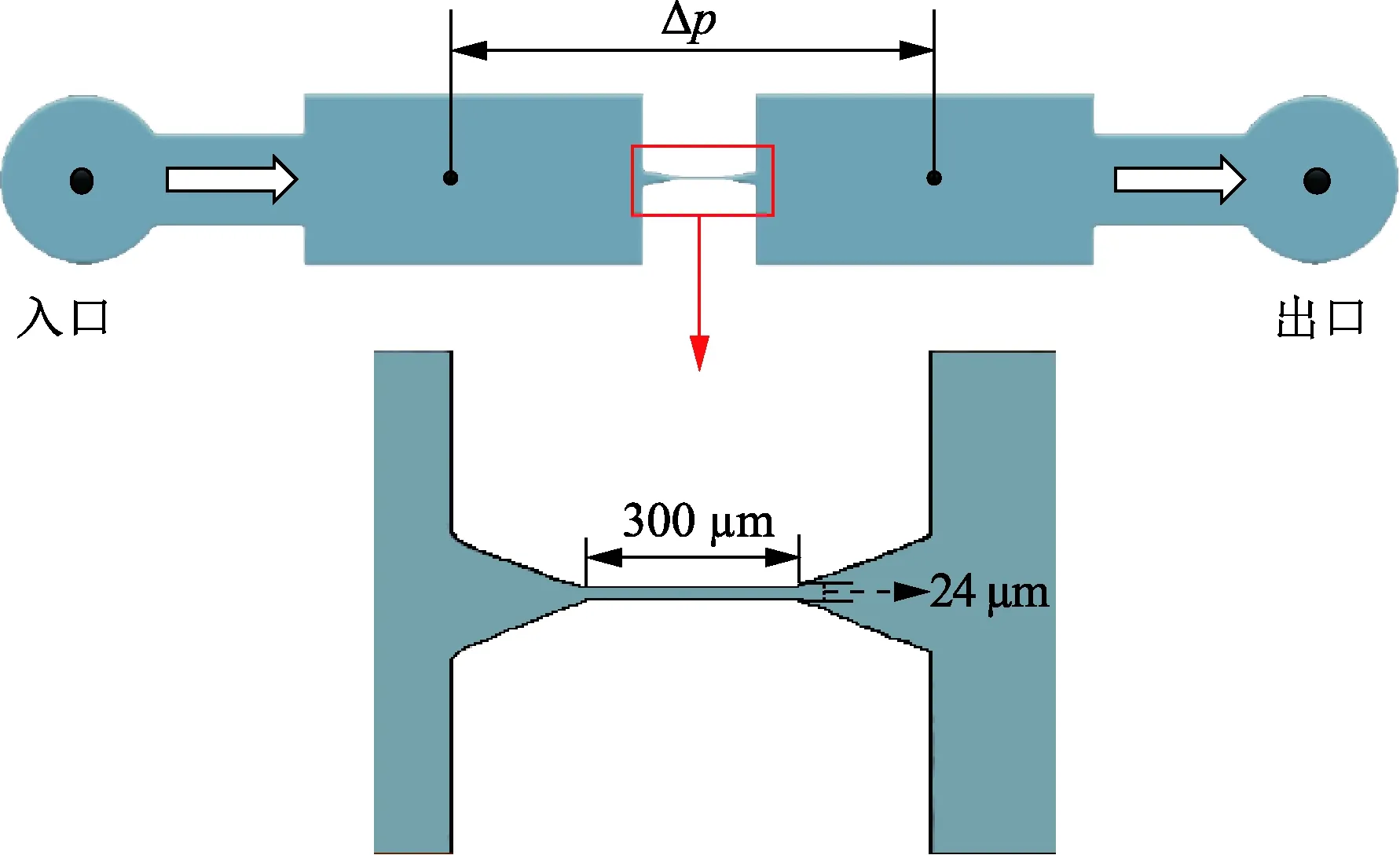
图1 微通道模型示意图Fig.1 Sketch map of microchannel model

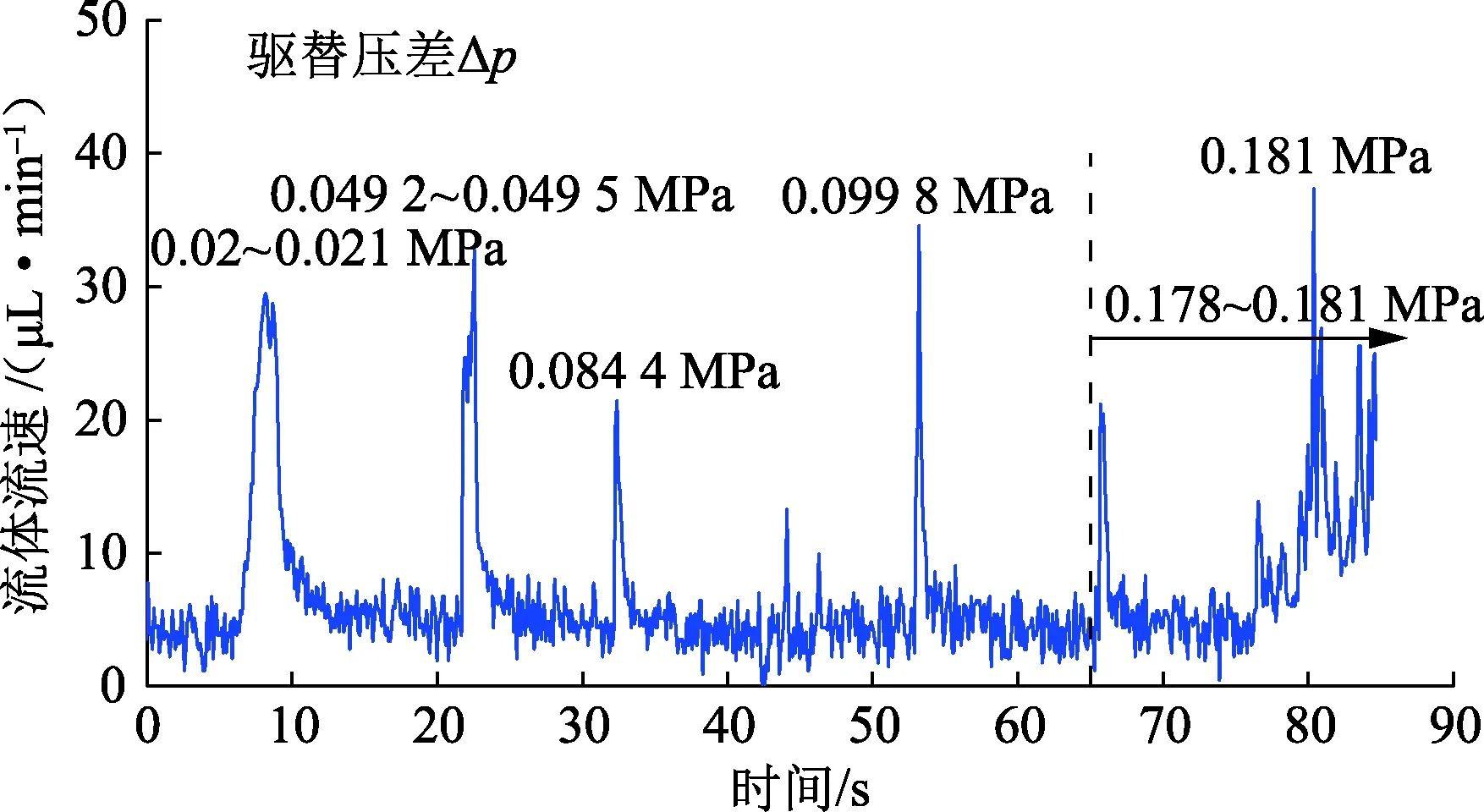
图2 微通道流速变化曲线Fig.2 Flow rate curve in microchannel model

凝胶颗粒流动处于周期性的堵塞和变形通过状态,导致流体流速持续大幅度波动变化,图2为微通道流速变化曲线。流动开始阶段,凝胶颗粒进入微通道发生堵塞;随着微通道两端压差增加至0.02～0.021 MPa,颗粒变形通过微通道,流速大幅上升;后续颗粒进入微通道后再次发生堵塞,流速迅速下降到较低水平;继续增加微通道两端压差到0.049 2～0.049 5 MPa时,颗粒又可变形通过,流速上升。如此往复,整个过程中流速不断波动,表现出非连续相流动特征。当微通道两端压差达到约0.181 MPa时,通道流速逐渐上升,说明颗粒可连续通过。

1.2 双管岩心流动实验

双管岩心流动实验装置包括注入系统、温度、压力测量控制系统和采集系统[5]。模型渗透率级差为6,实验温度为70 ℃,注入速度为1 mL/min。实验过程中,依次注入1VP(VP为孔隙体积)水、0.6VP质量浓度为2 000 mg/L的化学剂溶液、1.4VP的后续水,记录双管分流量变化。

两种化学剂溶液注入双管前后分流量变化曲线如图3所示。图3(a)表明:聚合物溶液注入前,高低渗管分流量比例稳定在约9∶1;聚合物溶液开始注入后,高渗管分流量有一定程度下降,低渗管分流量上升;聚合物溶液注入结束后,分流量恢复到初始水平。图3(b)表明:凝胶颗粒溶液注入前高低渗管分流量稳定在87∶13;凝胶颗粒溶液注入时高渗管的分流量迅速下降,低渗管的分流量迅速上升,并且两管的分流量交替波动;凝胶溶液注入结束后,高低渗管的分流量仍保持交替波动。与聚合物溶液注入相比,凝胶颗粒的不断堵塞和运移引起高低渗管分流量更大幅度的波动变化,且在后续注水过程中仍持续波动,表现出非连续相流动特征。

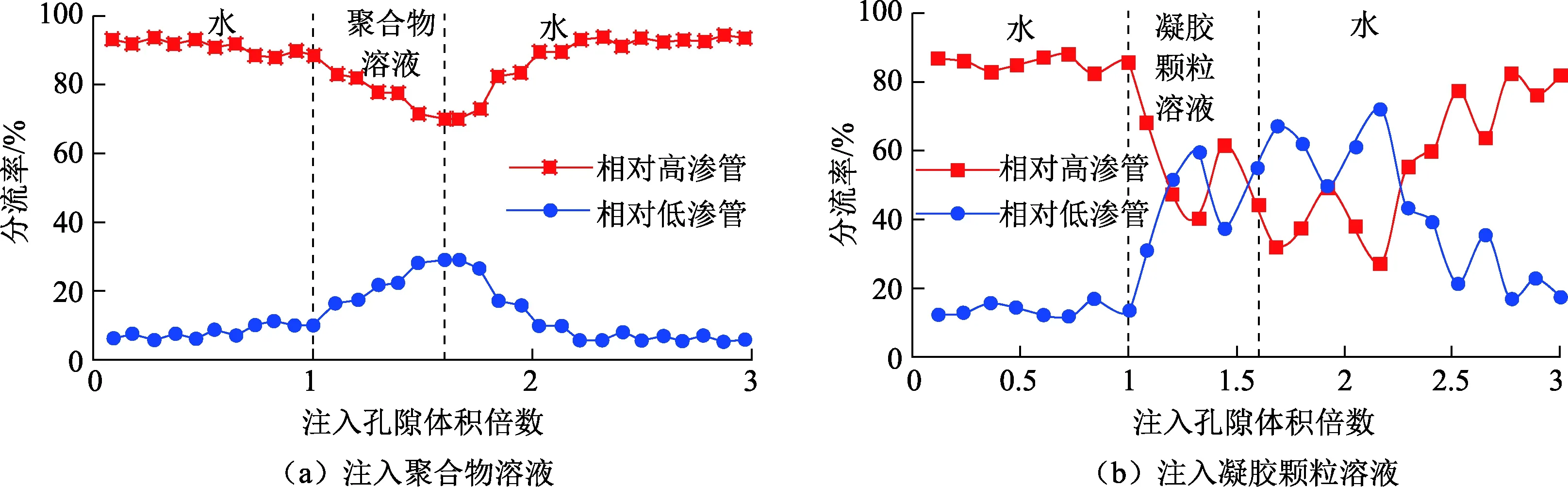
图3 双管岩心中分流量变化曲线Fig.3 Fractional flow curves in two rock cores

2 微观渗流模拟方法

非均相复合驱微观渗流特性应考虑凝胶颗粒、聚合物及表面活性剂特性。凝胶颗粒的流动除具有刚性颗粒流特征[6]外,还具有弹性变形特征[7];聚合物具有流体增黏、非牛顿流体流动等特征;表面活性剂具有油水界面张力降低、岩石润湿性改变等特征。选用格子玻尔兹曼方法(LBM)开展非均相复合驱微观渗流模拟,该方法在微观渗流模拟方面优势明显,其多相流模拟过程无需额外追踪油水界面,且可利用反弹格式简洁处理流体与壁面的作用[8]。模型采用Shan-Chen多相流LBM模型模拟油水流动[9],主要化学剂机制表征方法如图4所示,另外利用主动溶质法模拟表面活性剂传质扩散过程[10],通过调节松弛时间模拟聚合物增黏作用。

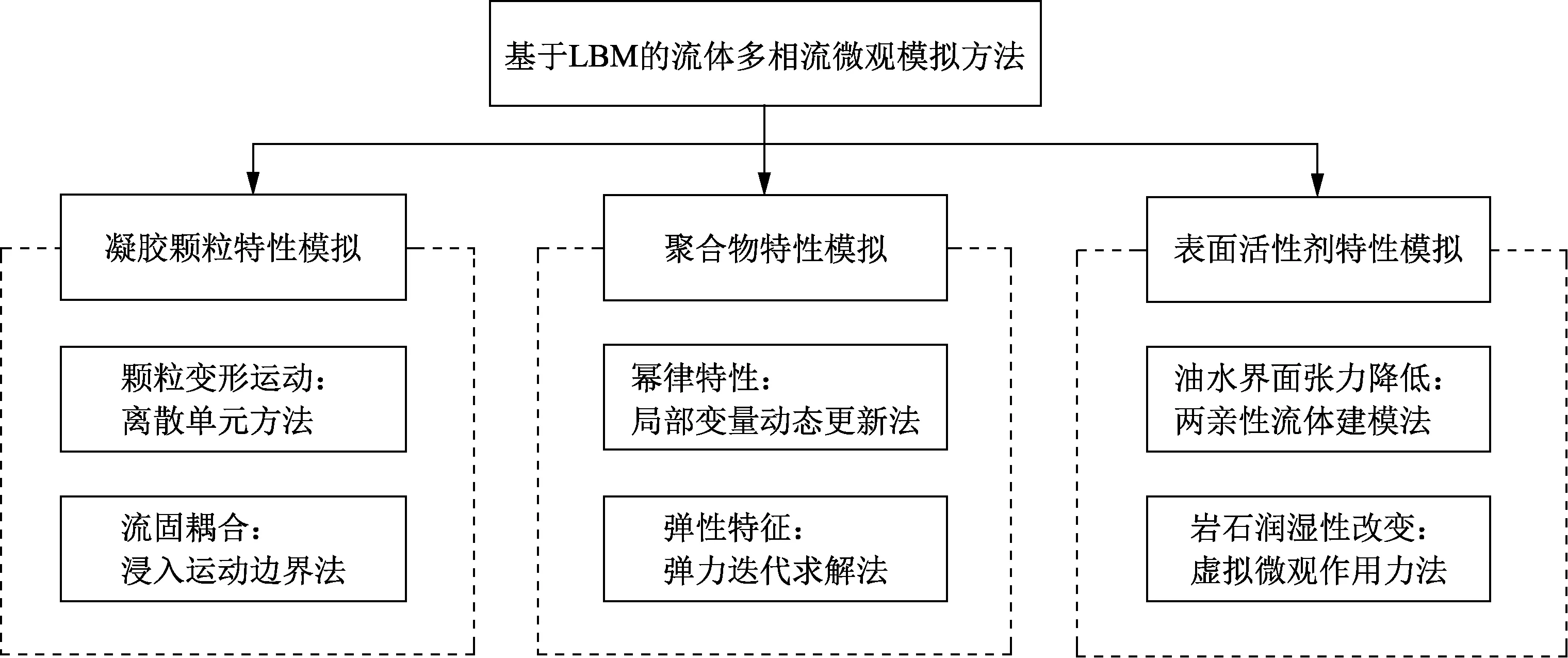
图4 非均相复合驱微观渗流模拟化学剂机制表征方法Fig.4 Mechanism characterization of chemical agents in microscopic seepage simulation of heterogeneous composite flooding

2.1 凝胶颗粒特性模拟

借鉴浸入边界法[11]的基本思想,将固体边界离散为一系列虚拟边界点,则凝胶颗粒原始曲线边界即可通过各边界离散点相连围成的多边形近似表示。凝胶颗粒变形及运移的模拟相当于各边界离散点相对位置变化和运移的模拟,如图5所示。

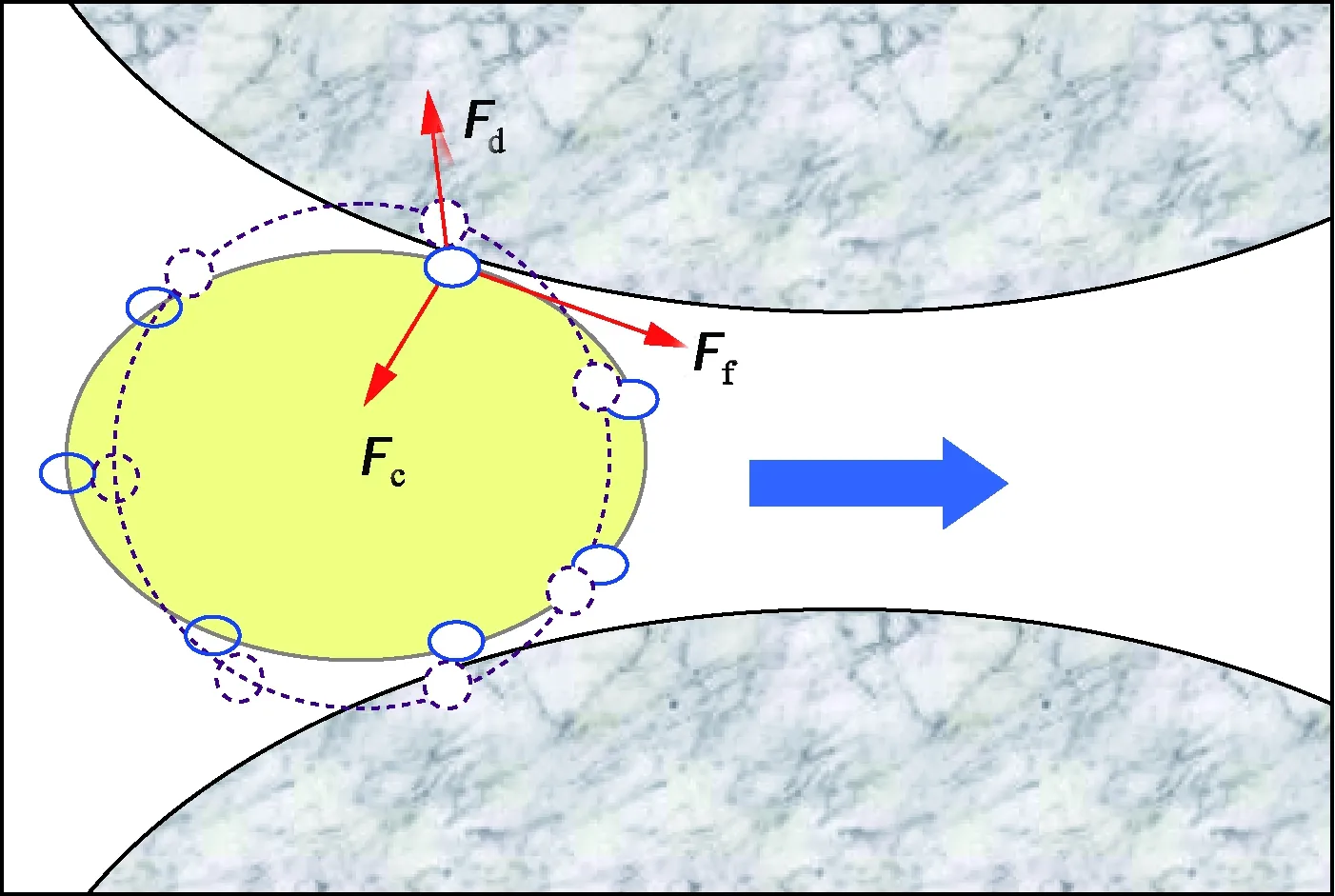
图5 凝胶颗粒弹性变形模拟方法示意图Fig.5 Schematic diagram of gel particle elastic deformation

根据牛顿第二定律,考虑各边界离散点受到的流固作用力Ff、固固接触作用力Fc和形变恢复力Fd,即可更新各边界离散点的速度和位置,其表达式为

ma=Ff+Fc+Fd,

(1)

v=vold+aΔt,x=xold+vΔt.

(2)

式中,m为边界离散点的质量,其值为凝胶颗粒质量与边界离散点个数的比值,kg;a为边界离散点的加速度,m/s2;Δt为时间步长,s;vold和v分别为边界离散点更新前后的速度,m/s;xold和x分别为边界离散点更新前后的位置。

流固作用力Ff采用考虑附加碰撞项的格子玻尔兹曼方法(LBM)[12]根据动量定理进行模拟计算,其表达式为

(3)

(4)

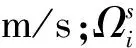
固固接触作用力Fc采用软球模型离散单元法(DEM)[13]进行模拟计算,其表达式为

Fc=Fnn+Ftt,

(5)

(6)

式中,Fn和Ft分别为颗粒间的法向作用力和切向作用力, N;n和t分别为单位法向向量和单位切向向量;kn和kt分别为法向和切向接触刚度,N/m;cn和ct分别为法向和切向阻尼系数,N/(m·s-1);δn和δt分别为法向重叠量和切向位移,m。

形变恢复力Fd反映凝胶颗粒弹性变形后促使其恢复至初始形状的作用力[14],其表达式为

Fd=Fbn+Fst,

(7)

Fb=Eb(β-β0),Fs=Es(lab-lab0).

(8)

式中,Fb和Fs分别为凝胶颗粒变形后离散边界点受到的弯曲形变恢复力和拉伸形变恢复力,N;β和β0分别表示凝胶颗粒变形前后相邻3个边界离散点之间的向量夹角, (°);lab和lab0分别表示凝胶颗粒变形前后相邻两个边界离散点之间的距离,m;Eb和Es分别为凝胶颗粒边界弯曲刚度和拉伸刚度。

2.2 表面活性剂特性模拟

表面活性剂是两亲性分子,在油水界面中极性的亲水基易与水相结合,非极性的亲油基易与油相结合,表现出在界面聚集的现象,进而降低了界面张力。参考两亲性流体建模方法[15],在LBM中将表面活性剂分子团抽象等价为具有一定浓度的偶极子,同时引进一个方向矢量演化偶极子平均排列方向,如图6所示。

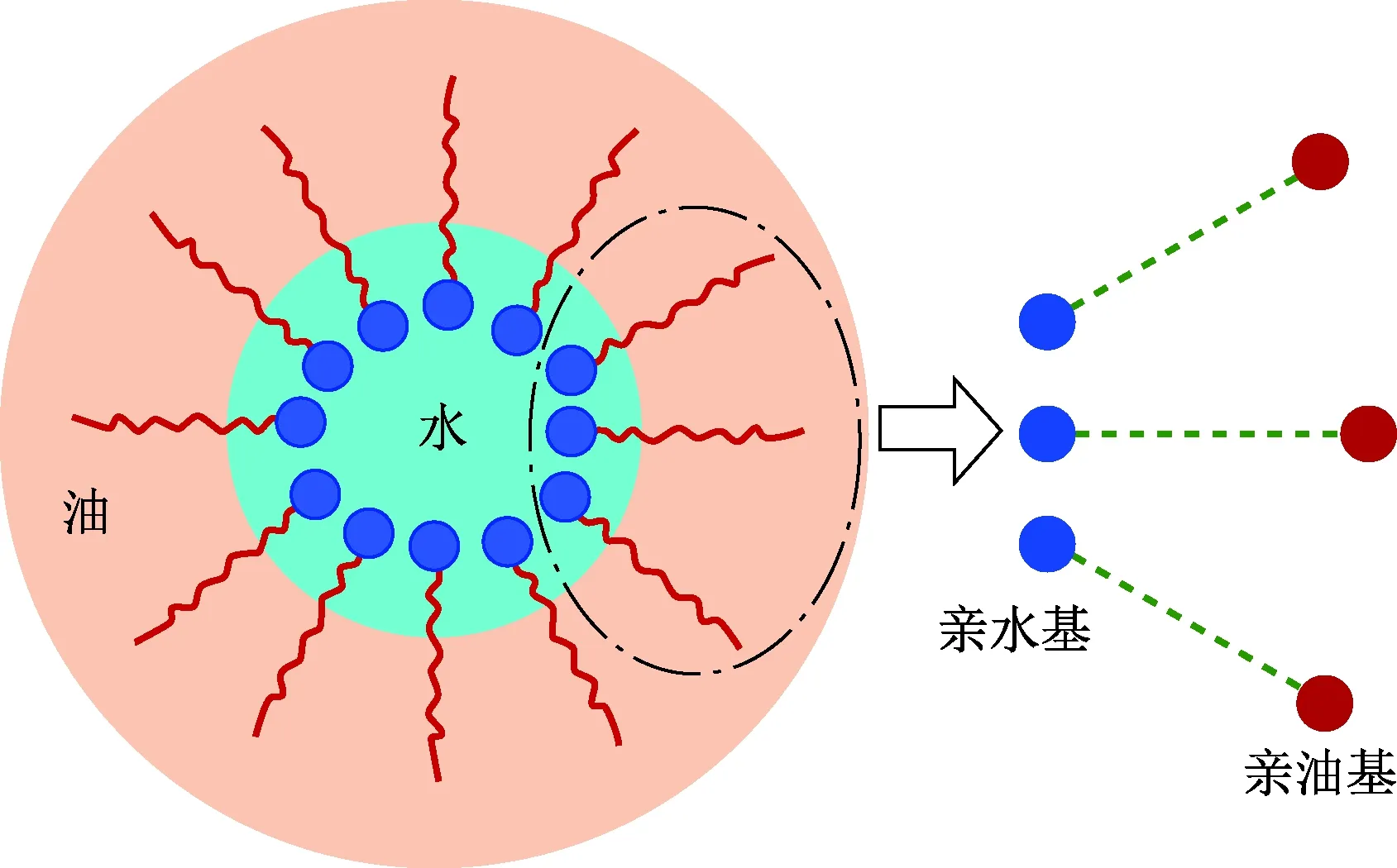
图6 偶极子等价模型Fig.6 Dipole equivalent model

偶极子两端电性不同,分别代表了亲水基及亲油基,其可与油水间产生吸引力或排斥力,力的作用通过牛顿第二定律体现。t时刻处于位置x处,油或水所受表面活性剂分子的作用力Fσs为

(9)

其中

式中,Gc,σs为油或水与表面活性剂间的作用强度;ρσ为油或水的密度,kg/m3;ρs为表面活性剂密度,kg/m3;d为偶极子排列方向;wi为权重系数;I为单位张量;D为格子维数。

表面活性剂受油水作用力Fsσ为

(10)

表面活性剂间的作用力Fss为

(11)

式中,Gc,ss为表面活性剂组分间的作用力强度;c为格子速度,m/s;“:”为双点积运算符,双点积的出现是由于相邻格点表面活性剂均为具有矢量方向的偶极子,需要利用张量运算将力场分配到不同方向。

表面活性剂在壁面的吸附浓度与壁面吸附强度有关,为此引入一个表面活性剂与壁面的微观作用力Fads,s以控制表面活性剂在壁面的吸附[16]:

(12)

式中,Gads,s为表面活性剂与固壁的作用强度;s为表示是否为固壁的指示函数。

表面活性剂会在岩石表面上吸附并影响岩石的润湿性,由于表面活性剂的吸附浓度与表面活性剂-固壁作用强度Gads,s成正比,且水-固的界面张力与水-固壁作用强度Gads,w成正比,可通过建立Gads,w与Gads,s的关系等价改变流固作用力实现润湿性改变[17],

Gads,w=Gads,w0+k1Cswallln(1+k2Gads,s).

(13)

式中,Gads,w0为初始的水与壁面的作用强度系数;Cswall为壁面表活剂质量浓度,g/L;k1和k2为系数,可用来调节润湿性改变幅度。

2.3 聚合物特性模拟

LBM中的流体黏度主要与松弛时间有关,考虑幂律流体特性时需要令松弛时间随局部剪切速率变化[18],进行局部动态参数更新,松弛时间τ可表示为

(14)

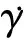
考虑黏弹性流体的弹性时可先根据流体本构方程及速度场计算出弹力,然后耦合到LBM模型中,通过改变速度场反映弹力的影响。速度场改变后又可重新计算弹力,如此反复迭代求解。以线性Maxwell黏弹流体为例,弹力Fel由应力张量的散度计算[19],表达式为

(15)

其中

τel=η/E.

式中,T为应力张量,N;η为聚合物表观黏度,mPa·s;u为流体速度,m/s;τel为记忆时间,s;E为弹性模量,Pa;t′为时间积分变量,s。

3 提高驱油效率机制

从扩大微观波及系数和提高微观洗油效率两个方面,基于微观渗流模拟方法揭示非均相复合驱油体系提高驱油效率机制。一方面,非均相复合驱油体系中可变形运移的“软固体”凝胶颗粒可引起流动增阻,迫使后续驱替液体转变流动方向,同时聚合物使驱替液黏度增加有效抑制黏性指进,从而达到扩大微观波及系数的作用;另一方面,表面活性剂的加入降低了油水界面张力,增加了分散油滴形变能力,同时改变了岩石壁面润湿性,导致油滴在壁面上的黏附功大大降低,从而提高了微观洗油效率。

3.1 颗粒暂堵升压后变形运移

为研究凝胶颗粒在孔喉中的变形运移过程,建立多喉道模拟模型,如图7所示。模拟区域长为1 300 μm,最宽处为200 μm,最窄处为40 μm。模拟过程中实时统计模型两端的驱替压差变化。

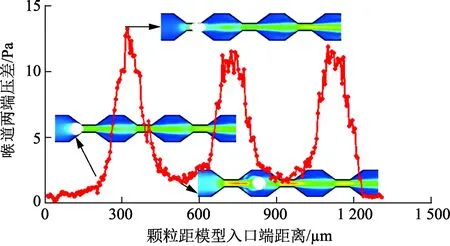
图7 凝胶颗粒通过孔喉时的压差变化Fig.7 Pressure difference variation when gel particles pass through throats

可以看出,当凝胶颗粒在水流携带作用下运移至喉道入口处时,由于压差较小,凝胶颗粒将暂时滞留堵塞,从而导致模型两端驱替压差升高;随着驱替压差的不断升高并达到凝胶颗粒变形通过所需的临界值后,凝胶颗粒开始变形并逐步向喉道内部运移;在壁面摩擦和颗粒变形作用的影响下,颗粒在喉道运移过程中,模型两端的驱替压差维持在较高水平;而当凝胶颗粒进一步运移通过喉道出口端时,模型两端驱替压差开始下降,凝胶颗粒也将逐渐恢复至其原始形状,并在流体携带作用下继续向前运移,直至到达下一喉道时再次重复这一过程[20]。因此,凝胶颗粒在多喉道模型中具有颗粒暂堵、升压后变形运移的微观渗流机制。

3.2 固液增阻导致液流转向

为研究凝胶颗粒变形运移对流体流动的影响,建立多孔介质模型,如图8所示。模拟区域长度为340 μm,宽度为100 μm。模拟并统计凝胶颗粒溶液流动过程中多孔介质两端的压差变化,并将其与纯流体流动时的压差比值定义为无因次流动增阻倍数[21]。

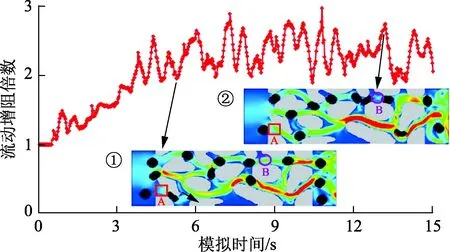
图8 多孔介质中凝胶颗粒溶液运移模拟结果Fig.8 Simulation results of gel particle dispersion system migrating in porous media

可以看出,随着凝胶颗粒溶液的注入,流动增阻倍数逐渐增加,直至达到一相对较高值后呈现持续波动状态。图8中①表明,由于凝胶颗粒滞留堵塞及变形运移引起的阻碍作用,A通道流体流量较小,而B通道由于没有凝胶颗粒影响,成为主要的液流方向之一。图8中②表明,由于A通道中凝胶颗粒已变形通过,颗粒阻碍作用消失,因此A通道成为主要液流方向,而此时B通道由于入口处颗粒堆积堵塞,流体难以流动通过,不再是主要液流方向。

由于凝胶颗粒在多孔介质中不断滞留堵塞、变形运移,导致各喉道流动阻交替变化,进而引起不同通道内流体流速交替变化,即固液增阻导致液流转向的微观渗流机制。

3.3 驱替液增黏抑制黏性指进

在毛细管数一定的条件下,一维均质多孔介质模型驱替过程黏性指进模拟结果如图9所示,其中无量纲界面长度为驱替前缘界面长度与多孔介质宽度之比。随着油水黏度比的增加,分形维数及无量纲界面长度增加,即黏性指进的自相似性提高,指状形状更细长,指进更明显,驱替突破时间更早。

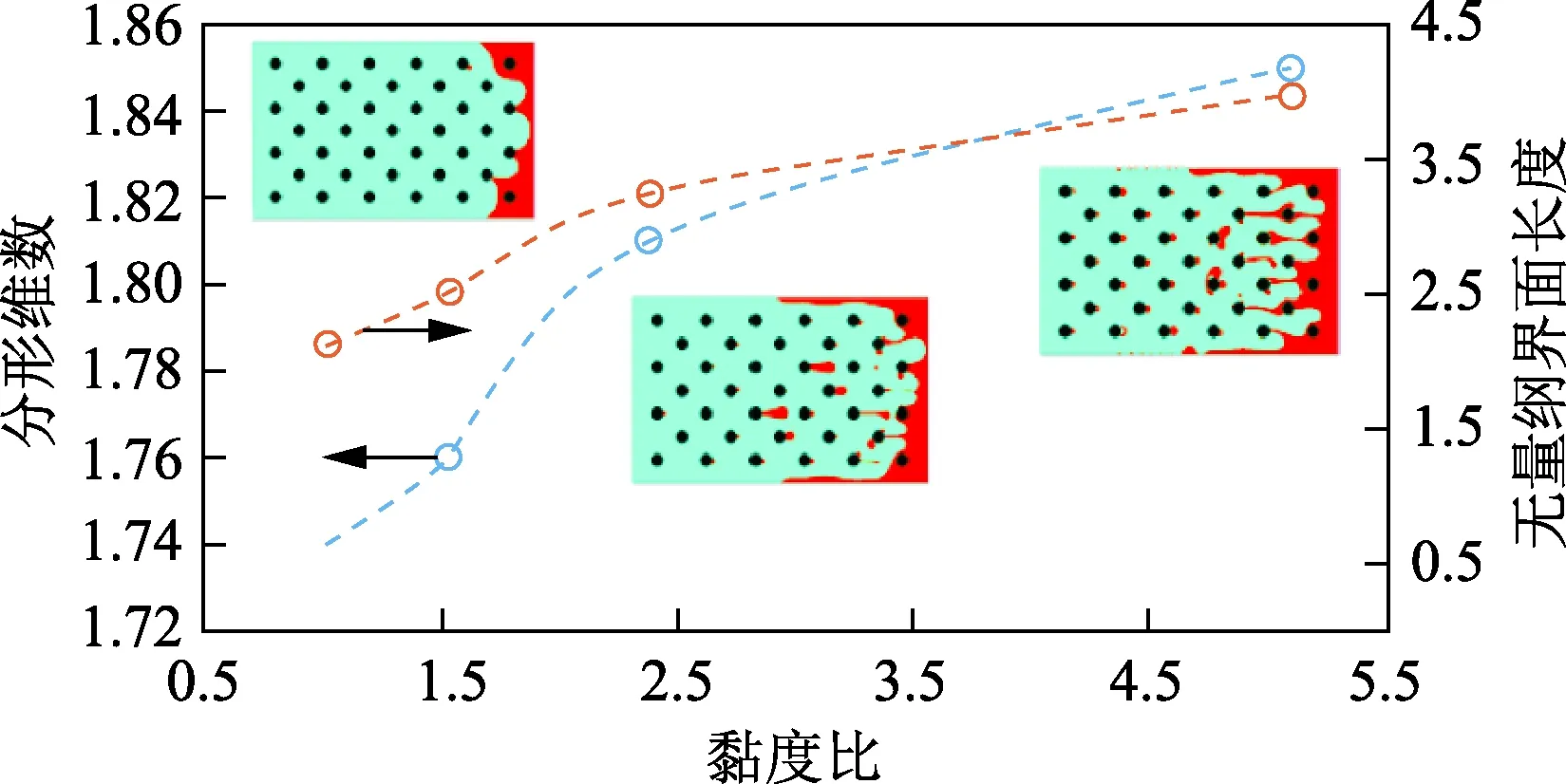
图9 油水黏度比对黏性指进的影响Fig.9 Effect of viscosity ratio on viscous fingering in porous media

在驱替压差一定的条件下,二维随机多孔介质模型(模型尺寸为2 mm×2 mm)中水驱、聚合物驱及非均相复合驱黏性指进现象对比如图10所示。

图10 水驱、聚合物驱及非均相复合驱二维驱替前缘对比Fig.10 Comparison of oil-water interface of two-dimensional displacement

在水驱过程中驱替前缘不均匀前进,指进现象明显,突破时刻模型角隅处及主流线中心残存大量剩余油;聚合物驱时驱替前缘推进更均匀一些,突破时驱替液波及范围更大;非均相复合驱时主流线中心的绝大部分油都能被驱替出来,角隅处的油得到有效动用,驱替前缘较其他方案最均匀,波及面积最大,驱替效果最佳。

非均相复合体系中由于聚合物加入增加了水相黏度,降低了油水黏度比,同时黏弹性颗粒起到了液流转向作用,因此可有效抑制复合驱黏性指进并扩大微观波及系数。

3.4 强化启动微观剩余油

水驱或聚合物驱后微观剩余油主要包括孔内分散型、壁面吸附型和角隅型剩余油等类型[22]。主要以赋存量较大的孔内分散剩余油及壁面吸附型剩余油为研究对象,讨论了非均相复合驱强化启动微观剩余油的作用。

图11为相同剪切作用强度下孔内分散油滴在不同表面活性剂质量分数下的最终形态。初始油滴形状为圆形,剪切流开始后,液滴在表面活性剂的影响下开始旋转、变形,逐渐从圆形变为椭圆或长条状,如图11(a)、(b)所示。如果最大形变状态时剪切作用不足以“卡断”液滴,则液滴在马兰戈尼力及毛管力下开始回缩,直到剪切力与马兰戈尼力、毛管力达到平衡。如果最大形变达到破裂界限,则油滴会进一步分散为子液滴,如图11(c)所示。总体上随着表面活性剂质量分数的增加,油滴更易变形甚至破裂,这主要是由于油水界面张力降低导致了毛细管数增大,大变形及小液滴形态也使油滴能更容易通过孔喉。

图11 剪切流中含不同表面活性剂质量分数的油滴形状Fig.11 Droplet shapes in shear flow with different surfactant mass fraction

设置岩石壁面原始状态为水湿,进行定压力梯度驱动模拟。模拟过程中微观数据模型中的表面活性剂质量分数与实际表面活性剂质量分数存在转换关系，可根据油水界面张力降低程度确定。不同表面活性剂质量分数下壁面附着剩余油的启动模拟结果如图12所示,其中无量纲启动压力梯度为剩余油启动压力梯度与界面张力之比[16]。随着表面活性剂质量分数的增加,界面张力降低,使原来不能从壁面剥离的油滴逐渐脱离下来,且表面活性剂质量分数越高,剥离程度越高;同时由于吸附导致了润湿性改变,吸附浓度越大,润湿性改变效果越好,油滴启动压力梯度降低,剥离程度大幅度增加。水湿情况下壁面附着剩余油所需要的启动压力梯度小,油滴可以完全剥离,而油湿情况下油滴的启动压力梯度大,且会有油膜吸附在壁面上而不能完全剥离。总体上非均相复合体系中表面活性剂降低了油水界面张力,改变了岩石壁面润湿性,使油滴在壁面上的黏附功大大降低,在低界面张力及润湿反转的双重作用下可使壁面剩余油启动压力降低90%以上,从而有效促进壁面吸附型剩余油的动用。

非均相复合驱过程中表面活性剂可增大孔内分散油滴的形变,促进油滴破裂,使油滴更容易通过孔喉,从而有效减小贾敏效应;同时可大幅度降低油滴在壁面的黏附功,降低壁面吸附型剩余油启动压力,最终有效提高微观洗油效率。