可视,可操作,可推理 让学生体验研究性学习
——《梯形的面积公式推导》教学实践探索
2019-11-01俞旭华韩伟珍
俞旭华 韩伟珍
梯形的面积公式推导是平面规则图形面积计算系列中,最后一种直边图形的面积公式推导。比较人教版、浙教版、青教版、西师大版、北师大版、苏教版等六个版本教材发现,所有教材都较为重视用多种方法推导梯形的面积计算公式,每个教材都基本提供三种教学思路。
综合各个版本的教材,我们进行梳理发现,梯形面积公式的推导方法大致有以下九种。

六个版本的教材中,有四个版本未提供数据,只有图片显示切割转化方法,没有梯形面积公式的推导过程;其余两个版本提供了梯形的数据,并有梯形面积公式的推导过程。
根据梯形面积公式推导的呈现方式,我们把学生的探究水平分成三个层次:

images/BZ_29_237_2449_363_2539.png平类别 达到的要求直观的探究水平 通过割、补、割补把梯形转化成已知图形,转化过程只要能画出直观图形即可。具体的探究水平 不仅会转化图形,而且通过测量或寻找合适的数据,还能计算出梯形的面积。形式化的探究水平 不仅能够画出转化的图形,还能计算出面积,最后推导出梯形的面积计算公式。
然而在教学实践中,笔者发现,一般梯形面积公式的推导都要教师予以暗示和启发:先引导学生复习推导三角形面积的转化方式,或者把平行四边形分割成两个完全一样的梯形,用这样的方式引导学生发现两个完全一样的梯形可以拼成一个平行四边形,由此推导梯形的面积公式。为什么要做这些铺垫和复习呢?因为很多情况下,能“独立自主”探究梯形面积公式的学生人数极少,所谓的探究,更多的是学生在教师的“指令”下机械性地“操作”。于是,我们进行思考:提供怎样的学习材料更有利于学生发现梯形的面积公式?如果提供了合适的材料,那在九种推导方法里,学生会发现哪几种?哪种方法出现的频率比较高?自主探究后,怎样进行反馈交流?
我们发现,以上六种版本中没有利用网格帮助学生推导梯形面积公式的方法。事实上,运用网格可以让图形的数据更明显,研究更可视化,因为推导平行四边形面积时,网格虽然仅用于数格子法,但不可否认,有了网格线做平行四边形的背景,学生对沿高剪下一个三角形补到平行四边形的另一端形成长方形,有更精准的认识。所以我们进行假设,在推导梯形的面积公式时,如果提供网格背景材料,可能会让学生的探究和发现更加主动、深刻,且推导梯形面积公式的方法更丰富,为此我们做了前测调查分析和报告。
研究主题:学生推导面积计算公式时需要用网格吗?——网格对学生推导梯形面积公式作用的调查计划与分析
一、调查目的
学生学习梯形面积公式前的认知起点调查与分析,主要调查学生在独立思考推导梯形的面积公式时有哪些不同的方法。
二、调查假设
提供网格背景对学生推导梯形面积公式的方法多样化和深刻性方面具有较大的影响。
三、变量控制
同年级平行班调查,(尽量控制平行班之间认知差异较小、教学进度一样)学生独立做题,控制时间为10 分钟,测查教师不干预学生思考。
四、变量差异
调查三个班的变量差异。
班1:只提供梯形图。
班2:提供网格背景的梯形图,且梯形的上底、下底、高的端点正好在格点上。

班3:提供网格背景的梯形图,且梯形的上底、下底、高和中位线的端点都在格点上。

五、调查样本选择
在笔者所在学校选择了五年级三个班的学生。(未对这三个班的学生教学过梯形的面积计算公式,但他们已经学习了三角形等面积计算公式的推导)
六、调查结果初步分析
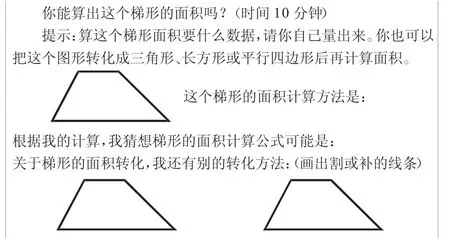
研究要求:请你算出这个梯形的面积。

研究结果统计表

0 0 0 0 0 0 0 0 0 4 3 0 3 3 0 3 3 0其他 0 1 1 0 1 1 1 1 1合计 11 11 1 18 19 10 23 21 15images/BZ_30_1299_385_1431_454.pngimages/BZ_30_1295_308_1440_373.png
1.只提供梯形图。(班1:34 人)
学生自己寻找数据或转化成其他图形后,算出梯形面积的学生占测试总数的32%,有68%的学生完全错误,其中有近10%的学生完全空白。在计算出梯形面积的学生中,把梯形分割成一个平行四边形和一个三角形的有3 人,分割成两个三角形的有2 人,分割成两个三角形和一个长方形的有2 人,补成平行四边形的有3 人。
2.提供网格背景的梯形图。(班2:36 人)
能正确算出梯形面积的学生占测试总数的53%,有28%的学生对梯形的面积公式进行了猜测,且推理正确。在计算出梯形面积的学生中,九种图形转化方法出现了七种,其中倍拼法、分割成两个三角形、分割成一个平行四边形和一个三角形的方法,学生能在格点背景图的帮助下算出面积后,更顺畅地推测出面积计算公式。
3.提供网格背景的梯形图。(班3:32 人)
能正确算出梯形面积的学生占测试总数的66%,有47%的学生对梯形的面积公式进行了猜测,而且推理正确。在出现的所有方法中,图形转化频率最高的方法是分割成两个三角形和一个长方形。在算出梯形面积的学生中,九种图形转化方法出现了八种,公式推导最顺畅的方法是倍拼法、分割成两个三角形和沿中位线对折剪开把两个梯形拼成平行四边形这三种。
综上所述,根据前测调查,学生对于梯形面积计算公式的推导,利用网格做背景,且上底、下底、高和中位线的端点都在格点上,更具可视性,学生更易操作、更能理解、推理、推导出梯形的面积公式,并能进行多样化理解,使思维更加具有灵活性和深刻性。
【教学过程】
一、抛出问题,引导转化
师:这个梯形的面积指哪部分?
师:你有办法算出这个梯形有多大吗?(学生口答分成两个三角形或分成平行四边形和三角形等)
师:是的,变成三角形、变成平行四边形就好算了,因为这几种图形我们已经会算了,这种方法极好,我们称之为“转化”。(板书“转化”)
师:刚才已经有同学说到把梯形分成两个三角形,这样的转化方法可以简称“分”;(板书“分”)像推导三角形面积的时候,我们把两个完全一样的三角形拼成一个平行四边形,这样的转化方法叫“合”,(板书“合”)在推导平行四边形面积的时候,用到“移”和“补”。(板书“移”“补”)
师:这节课,我们就要运用以前学过的知识,通过“分”“合”“移”“补”,把梯形转化成我们学过的图形,算出它的面积,并探索梯形的面积计算公式。
【设计意图:化归思想是教学平面图形面积系列的方法基础,从教材编者的角度看,化归思想在平行四边形面积推导时是“有指导的探究”,在三角形面积推导阶段是“有指导的应用”,在梯形面积推导阶段应该是“自主应用”化归思想,所以设计中,以解决问题导入,让学生在方法的探索中,从无意识走向有意识,对化归思想方法有更明确的认识,才有自主应用。】
二、分合移补,自主建构
1.学生使用《探究作业单》完成探究任务。(提供带网格的梯形图,且相应边的端点在格点上)
任务一:算出梯形的面积。
任务二:对比新图形与梯形的面积关系以及新图形的边与梯形边的对应和关系。
任务三:根据计算梯形面积的算式,猜测梯形面积的公式。
(学生探究,教师进行指导,特别关注学困生,及时给予指导。教师在巡视中,也要关注学生自主探究时出现频率更高的方法)
2.反馈交流。
(1)四人小组交流。
师:说一说,你是怎么算出梯形的面积的?说一说,梯形与新图形的面积以及边的对应关系。说一说,梯形的面积公式可能会是怎样的?为什么?
师:相互交流后,把你们认为最好的转化方法,画在大图上,准备全班交流。
(2)全班交流。
师:每个小组把你们认为最合适的方法转化图贴在大屏幕上,请小组派两人合作汇报和板书。如果有方法类似的小组,请听后进行补充。
课堂中形成有侧重的几种梯形面积公式的推导:
●推导一:梯形的面积=平行四边形的面积
(2+8)×(4÷2)=20cm2
面积=(上底+下底)×(高÷2)
●推导二:梯形的面积=平行四边形的面积
(2+8)÷2×4=20cm2
取长补短,平行四边形的底是梯形
上底下底和的一半
面积=(上底+下底)÷2×高
●推导三:梯形的面积=平行四边形面积的一半
(2+8)×4÷2=20cm2
面积=(上底+下底)×高÷2
●推导四:梯形的面积=两个三角形的面积之和
2×4÷2+8×4÷2=20cm2
面积=上底×高÷2+下底×高÷2

推导一

推导二

推导三

推导四
(3)举一反三,代数思维。
生:同一个梯形,我们用不同的转化方式推导出了这么多的公式,那么梯形的面积公式到底是什么呢?它们之间有什么联系呢?
师:其实这几个面积公式是一样的,我们通过整理可以发现,它们都可以变成“(上底+下底)×高÷2”的形式。用字母表示是S=(a+b)×h÷2。
(4)课件呈现所有的转化方法。
师:(课件呈现所有的转化方法)如果把这九种转化方法按照分、合、移、补分类,各是哪几种?
(3、5、6 为分,2 为合,9 为补,1、4、7、8 为移。课件归并展示分类)
【设计意图:这节课,我们希望学生经历用分、合、移、补等方法探索梯形面积计算方法的过程,培养空间观念;经历方法的交流诠释、转化沟通、抽象概括过程,掌握梯形的面积计算公式,培养代数思维能力。因而课堂重点在开放探究和归纳沟通,所以这两个环节应给予学生充分的时间思考、计算、交流、沟通。特别在反馈阶段,由于涉及方法太多,切忌平均使用力量,所以在开放探究和小组交流的基础上沟通归纳,对各类方法有所侧重,而学生最容易想到的分的方法,可以作为计算组合图形面积的思路。】
采用带网格的梯形进行教学,杜绝了教师指引下的“操作木偶”,让学生带着想解决的问题对梯形进行“分”“合”“移”“补”,转化成学过的图形,自主性强。转化后的图形与原梯形面积、对应边之间的关系一目了然,使研究具有可视性。由于研究材料的更新,促使图形转化的难度降低,学生不但轻松理解转化思想的优越性,而且使研究更加深入,对梯形面积公式的归纳、发现和推导更充裕。可视、可操作、可推理,学生经历了把新图形转化成已知图形、从具体数据计算到推导梯形面积公式,最后代数化思维得到梯形面积字母公式,这样的过程让学习真实发生,让学生体验探究性学习的乐趣,这正是本课研究价值所在。
