基于PCA-AHP-IE的多指标评价模型研究与应用

(浙江工业大学 计算机科学与技术学院，浙江 杭州 310023)

高校专业评价是指多个高校在某一专业上优劣比较结果，为全面、准确地表示评价结果，在高校专业评价的过程中需要以多个指标为准则[1-3]，由于高校专业评价指标涉及面广、数据间差异大，因此解决该问题的评价方法需要在考虑以上因素的同时兼顾传统观念因素。目前被广泛应用到多指标评价分析的方法主要有主成分分析法[4-5]、模糊综合评判法、TOPSIS评价法、灰色关联度分析法和熵权法等。文献[6-10]将层次分析法(AHP)运用到威胁评估、质量评价等问题上，虽然可以快速、简便地得出评价结果，但是评价过程过于依赖专家知识体系，获得的指标权重和评价结果缺乏客观依据。文献[11-12]通过对熵权法进行改进并应用于实际评价问题中，虽然一定程度上改善了指标权重精确度，但是仍然会因为数据极端多寡导致评价结果失真。文献[13-19]将多种评价方法结合建立多指标评价决策模型，各模型都一定程度地降低了对人为因素的依赖、增加评价结果的稳定性，但在主、客观权重融合及评价结果的精确度上还有待提升。

笔者提出一种多组合赋权评价模型，通过主成分分析法提取原始样本主成分，实现对复杂样本数据的降维处理，在层次分析法执行中引入多专家打分及熵值概念，并与熵权法获取指标权重综合加权求得综合权重，既大幅度减轻了指标权重对专家经验的依赖，又避免数据极端多寡导致的指标权重失调，最后采用二次加权的方式获取更准确的评价结果，并将这种多指标评价模型应用到高校专业评价问题中。

1 高校专业评价指标体系构建

以各高校在计算机专业中排名问题为例，为该多指标评价问题构建指标体系，基于指标选取的契合性、针对性、系统性和科学性原则，参照层次分析法的关系模型，根据该问题的支配关系形成指标体系层次结构，如表1所示。表1中：新生质量、就业竞争力、科研力量和学校实力为一级指标体系；二级指标体系由计算机专业在该校的录取分数线、录取最低名次、该校计算机专业学生总数、该校计算机专业学生的就业率、升学率、专业就业对口度、就业后的满意度、雇主满意度、平均薪酬、计算机专业教师学生发表论文单篇引用数、H指数、发表论文数、计算机专业老师数、教授的比例、高校批次及高校办学地的城市等级16 个指标组成。在前期的研究中，发现科研力量及学校实力等多项指标均成线性相关，解释的信息有重叠，因此基于对信息的高效性与简洁可操作性原则，科研力量主要从论文产出来做解释。

表1 高校专业排名指标体系Table 1 University professional ranking index system

2 PCA-AHP-IE评价模型

在高校专业评价原始指标体系中二级指标变量较多，且多指标数据之间通常具有一定的相关性，得到的评价结果往往效果较差。用层次分析法(AHP)求多指标权重时，重要性判断过于依赖专家的知识体系和经验，评价结果很大程度受到主观因素的影响。高校专业评价问题受多个指标的影响，精度要求较高，对于多指标的子层指标体系评价准则往往偏差较大；熵权法(IE)求指标权重的结果完全取决于客观的样本数据，因此原始数据的差异性决定了权重的大小，而实际应用中往往存在许多特殊数据导致获取的权重与人们的常识相差过多。笔者通过改进、结合3 种多指标评价算法，来得到更加客观、稳定的权重。利用PCA的降维思想结合样本数据的差异性来选择综合排名指标，实现对不同量纲单位数据的归一化处理，从而构造性质较好的样本数据，更准确地映射评价结果。表1中高校专业评价指标体系一级指标属于对高校专业评价领域相对抽象的主观认知，二级指标为样本数据的客观映射，首先通过引入多专家打分机制和熵值概念改进层次分析法，分别获得一级指标和对应的二级指标的权重，从而消除传统层次分析法中1～9标度对多指标间重要差异性难区分的问题，同时很大程度上避免权重计算因过于依赖人的主观意识致使评价结果有失客观性及准确度的问题；然后采用熵权法对下层指标体系求权重，将层次分析和熵权法得到的指标体系权重进行一系列的综合加权处理获得综合指标权重，最后对综合指标权重采用二次加权的方法求评价结果，从而兼顾所有评价指标的影响，避免指标权重失调引起评价结果的失真。具体步骤如下。

2.1 指标体系降维处理

假设高校排名实例样本数据中有n个样本，指标评价体系中有k个一级指标，m个二级指标项，则可构成由样本和指标项数据组合的原始矩阵Y=(yij)n×m，其中yij表示第i个高校对象在第j个排名指标上的值。

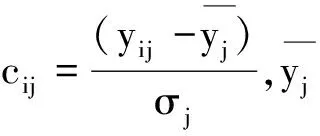
(1)

2) 依据标准化矩阵均值为0，方差为1的规则，计算标准化矩阵C的相关系数矩阵R为

(2)

(3)

4) 通过选取在主成分中载荷量较大的r个指标来作为新指标体系的二级指标，代替原有的样本指标项来表示所有的样本信息，构成综合指标体系。

2.2 改进层次分析法求指标权重

对上述综合指标体系中的一级指标及对应的二级指标求解权重，以k个一级指标求解为例，为指标重要性设置100 分制评分表，如表2所示。采用v个专家分别对各指标重要性打分，再结合1～9 标度法(表3)对指标重要性分值进行两两比较建立v个判断矩阵，第q个判断矩阵为

Pq=(pqij)k×k

式中pqij为第q个专家比较矩阵中第i个指标比第j个指标的重要度，则第q个专家判断矩阵对应的权重集合记为wq，且wqi表示根据第q个专家指标评分得到的第i个指标权重，其计算式为

(4)

式中zi为中间变量，表示第q个专家指标评分中第i个指标的相对权重，通过对k各指标的相对权重进行归一化处理，得到第q个专家指标评分得到的第i个指标权重wqi。对第q个专家判断矩阵进行一致性检验，其计算式为

(5)

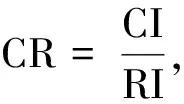
(6)

将一级指标权重向量记为B={β1,β2,…,βk}，同理求出一级指标对应的二级指标权重向量记为Φ={φ1,φ2,…,φr}。

表2 指标重要度评分表Table 2 Index importance score

表3 1～9标度法规则表Table 3 Levels scale method

表4 平均随机一致性指标Table 4 RI index

2.3 IE求二级指标权重

1) 根据主成分分析法确定的n个高校样本及r个综合排名二级指标项组成原始矩阵T为

T=(tij)n×r

对T进行标准化处理，包括对去除排名指标单位不同造成的影响而进行的无量纲化处理和为减少指标数据极端值对排名结构的影响而进行的归一化处理，得到标准化矩阵为A=(aij)n×r，aij可表示为

(7)

式中：tmax，tmin分别为原始数据中最优值与最差值。

2) 根据数学上熵值的定义可得出第j个评价指标的熵值为

(8)

式中：sij为第j个指标在第i个样本下的比重；熵值Ej取值为0～1。

3) 根据得到的熵值，定义熵权法权重向量为Ψ={ψ1,ψ2,…,ψr}。熵值与熵权呈现反比关系，熵权越大，熵值越小，说明该指标在评价体系中作用越重要，熵权为

(9)

2.4 综合权重加权求评价结果

1) 将改进层次分析法得到的二级权重Φ={φ1,φ2,…,φr}，结合熵权法得到指标权重Ψ={ψ1,ψ2,…,ψr}，计算二级指标综合权重为T={t1,t2,…,tr}，其计算式为

(10)

2) 按照主成分分析得到的k个一级指标与r个二级指标的对应关系，对综合指标权重T重新定义为T={t11，t12，…，t1n1，…，tk1，tk2，…，tknk}，其中tini即第i个一级指标对应的第ni个二级指标权重，ni表示第i个一级指标对应的二级指标数。分别对第i个一级指标对应的二级指标综合指标进行归一化处理，结果记为Ω={ω11,ω12,…,ω1n1,…,ωk1,ωk2,…,ωknk}，其中ωij为

(11)

3) 将一级指标权重向量B与综合二级指标权重向量Ω进行2 次加权，得出高校专业评价模型为

(12)

式中xikl为第l个高校专业在第i个一级指标对应的第k个二级指标项对应的样本数据，这种2 次加权模型很好地将主、客观权重组合到一起，保证了评价模型的科学性、稳定性及准确性。

3 实例应用

实例选取116 个高校的计算机科学与技术专业的16 个评价指标在2016 年各项数据作为实验样本数据，即样本n=116，指标项m=16。

1) 将上述116 个样本，16 个排名指标项数据作为原始矩阵，对原始样本矩阵进行同一量纲下的标准化处理，计算出关系矩阵R，利用SPSS工具计算相关矩阵R的累积贡献率等，如表5所示。

表5 样本总方差分解表Table 5 Total varlance explained

由表5可知：前4 个主成分的累积贡献率为82.5%，超过80%，基本代表了原始样本的所有信息量。根据载荷矩阵规则得出：第1个主成分主要由C7(就业满意度)，C8(雇主满意度)，C9(平均薪酬)，C15(高校批次)决定；第2 个主成分主要由C10(单篇引用数决定)，C11(H指数)，C14(教授占比)决定；第3 个主成分主要由C1(录取分数线)，C2(录取最低名次)决定；第4 个主成分主要由C16(办学地城市等级)决定。上述10 个排名指标分别在4 个主成分中载荷较大，可代替原有的16 个指标，大大减少了需要分析的变量数。

2) 从上述116 个样本中选取80 个样本数据比较完整的高校结合主成分分析得出的10 个主成分排名指标组成的新矩阵进行相关性检验，考察指标间的联系和区别及指标的交叉影响，实现对指标体系的优化。从检验结果(篇幅有限，此处不赘述)得出多项指标存在相关性关系，考虑同一量纲下对于样本中缺失项数据的两种处理方法为(1) 替代转化：由样本数据结论可知，雇主满意度和就业满意度存在可替代关系，利用线性回归系数加以处理，可以较为合理地解决满意度数据，因此可将这两项整合为一个综合指标；(2) 相关性均值填充：因为数据显示，多项指标的数值浮动较大，故不适合用全体均值来填充缺项，但发现各项指标间的相关性存在显著，如若A校缺少P指标，P指标与Q指标显著线性相关，高校按照Q指标排名，取A校临近4 个高校P指标均值进行填充。

依据以上规则，结合主成分分析法得到综合指标体系的二级指标集合为S={录取分数线，录取最低名次，就业满意度，平均薪酬，单篇引用数决定，H指数，教授占比，高校批次，办学地城市等级}，对116 个样本中的缺失项数据进行补全后得到矩阵T，表示为

T=(tij)n×ri=1,…,n;j=1,…r;n=116;r=9

3) 高校专业评价综合指标体系一级指标集合Z={新生质量，就业竞争力，科研力量，高校实力}，利用改进层次分析法求综合指标体系权重。参考3 位专家对综合指标体系的评分意见，可构成一级指标打分矩阵A为

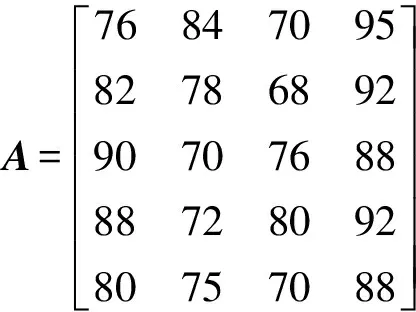
以一级指标求权重为例，根据每个专家的评分情况，结合1～9 标度法构成5 个判断矩阵，对第i个矩阵通过式(4)求出第i个专家评分对应的指标权重向量Wi，并通过一致性检验获取满足一致性要求的指标权重向量。即W1={0.226，0.293，0.165，0.316}，W2={0.257，0.231，0.103，0.409}，W3={0.308，0.199，0.207，0.286}，W4={0.297，0.145，0.239，0.319}，W5={0.273，0.233，0.177，0.317}。将得到的3 个一级指标权重向量组合成权重矩阵W。

对权重矩阵W利用熵值概念，通过式(6)求出指标相对客观权重向量B={0.293，0.203，0.113，0.391}，同理利用改进的层次分析法分别求出一级指标对应的二级指标向量Φ={0.761，0.239，0.376，0.624，0.733，0.267，0.275，0.479，0.246}，如表6所示。

表6 改进层次分析法求指标权重

Table 6 Improved analytic hierarchy process to obtain index weight

总体目标评价准则评价指标高校专业评价A新生质量(0.293)录取分数线(0.761)录取最低名次(0.239)就业竞争力(0.203)就业满意度(0.376)平均薪酬(0.624)科研力量(0.113)论文单篇引用数(0.733)论文产出H-指数(0.267)高校实力(0.391)教授占比(0.275)高校批次(0.479)办学地城市等级(0.246)

4) 熵权法求综合指标体系二级指标权重，参照式(7)对主成分分析法得到的矩阵T进行标准化处理，得到矩阵A作为熵权法的标准化矩阵，指标项集合为S，得到的权重集合为φ={0.053，0.242，0.138，0.116，0.211，0.105，0.034，0.066，0.035}。然后，参照公式(10)，将熵权法获得的二级指标权重φ，结合改进层次分析法得到的二级权重Φ求得综合二级指标权重集合T={0.089，0.127，0.114，0.159，0.34，0.062，0.02，0.07，0.019}。参照式(11)对综合二级指标权重进行归一化处理得当标准化综合二级指标权重Ω={0.412，0.588，0.418，0.582，0.846，0.154，0.184，0.642，0.174}。

最后利用加权评价模型式(12)对改进层次分析法得到的一级权重B及综合二级指标权重Ω进行二次加权求解，求得高校专业评价结果。表7为笔者评价模型及层次分析法得到的部分高校在计算机专业上排名结果，根据层次分析得到的结果中武汉大学排名明显高过北京邮电大学，因为层次分析法专家经验给出的录取分数线权重较高，而武汉大学在录取分数线高于北京邮电大学，而其他大部分指标数据较为劣势的情况下得到较高的排名，这与传统观念相差甚远。经验证，笔者提出的评价模型获得的评价结果具有较高的准确度和稳定性，该评价模型合理、可行且易操作。

表7 计算机专业高校排名Table 7 University rankings in computer science

4 结 论

笔者通过改良高校专业评价的指标设计体系，提出了基于PCA-AHP-IE的多指标评价模型，很好地避免了评价结果过于依赖主观经验或客观数据，也避免了因数据极端多寡或专家知识库结构不同而导致评价结果与人们的正常认知或实际情况不符的情景，既符合样本数据的内在规律，又能满足专家及大众的普遍认知。该评价模型可以有效、合理地应用到高校专业评价这类多指标评价研究中，但是算法仍存在一些不足之处，指标体系仍受限于数据的不完善，希望在以后的研究中继续改进。