On the friction effects on rigid-body penetration in concrete and aluminium-alloy targets

C.G.Chi ,A.G.Pi ,Q.M.Li ,F.L.Hung

a Institute of Chemical Materials,China Academy of Engineering Physics,Mianyang,Sichuan,621900,China

b State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing,100081,China

c School of Mechanical,Aerospace and Civil Engineering,University of Manchester,Manchester,M13 9PL,UK

Keywords:Penetration Friction Concrete Aluminium

A B S T R A C T The friction on the projectile shank is usually excluded in the penetration analysis due to the difficulties to measure the pressure and frictional coefficient.In this article,the frictional force on projectile shank is discussed indirectly through the comparison between experimental data and empirical/analytical formulas of the penetration depth for both concrete and aluminium-alloy targets.It is found that the effect of the frictional force along the projectile shank can be further discussed by the afore comparison and discussion and cannot be ignored because of the relatively large effecting area,especially for deep penetration of concrete and aluminium-alloy targets,where the friction will account for more proportion of penetration resistance.

1. Introduction

The frictional force on the projectile shank is usually excluded in the penetration analysis due to the difficulties to measure the pressure and frictional coefficient between the projectile shank and target under such extreme conditions.There are limited researches on this issue.Rosenberg and Forrestal[1]conducted a series of perforation tests on 6061-T651 target plate using normal and reduced-shank projectiles with conical head shape.It indicated that about 10%reduction of the ballistic limit can be caused when a reduced-shank projectile was used. Ref. [2] used normal and reduced-shank projectiles with ogival head shape in the penetration into concrete target, and the penetration depth for the reduced-shank projectile increased more than 10%when compared with the penetration depth of normal projectile.However,in a study of deep penetration into 6061-T651 target by normal and reduced-shank projectiles with hemi-spherical head shape in Ref.[3],it was found that the frictional force on the projectile shank has very small influence on the penetration depth.

Furthermore,a general analytical solution of the penetration depth was derived in Ref.[4]based on non-dimensional impact factor I0(defined later in Eq.(13)),i.e.P/d=2I0/π,where P is the penetration depth,d is the diameter of the projectile.Meanwhile,an empirical equation, P/d= I0/2, was also proposed, which agreed better with wide range of experimental data for deep penetration than the afore analytical equation.However,the reasons why the empirical equation was better than the analytical equation was not explained in Ref.[4].

In this article,the frictional force on the projectile shank is included in the penetration resistance and the analytical solution for the penetration depth under such situation is obtained,based on which,the analytical predictions of the penetration depth for both concrete and aluminium-alloy targets are compared with a range of experimental data as well as the analytical and empirical equations.

2. Rigid-body penetration with considering friction on projectile shank

The normal stress σnon the projectile head perpendicular to projectile surface is commonly given by Ref.[5].

where Y and ρtare the yield stress and density of target material,respectively;A and B are non-dimensional material constants,related to the effects of strength and inertia of target material;vnis the material particle velocity normal to the surface of the projectile head which can be determined by the penetrating velocity v of a projectile according to vn=vcosθ;The tangential stress on the head is presumably determined by the friction on the interface,σt=μσn,where μ is the sliding friction coefficient on the projectile-target interface.

When the projectile shank enters into the tunnel which has been opened by the projectile head,the pressure of expansion Bρtv2nin Eq.(1)would decrease to 0,because there is no further expansion and the expanding velocity v on the projectile shank changes to 0.Then the pressure on the shank can be derived as psh=AY,as suggested in Ref.[6].This is valid when cavitation does not occur if the impact speed is not sufficiently high[7].

Taking the frictional force on the projectile head and shank into account,and using the same derivation procedure as that in Ref.[4],the axial resistance on the projectile can be expressed as

where N1and N2are integral constants according to projectile shape,shown in Eq.(4)-Eq.(7);ρtis target material density;v is penetrating velocity;L0and h are overall lengths of projectile and height of projectile head,as shown in Fig.1.

For deep penetration where the effect of the entrance stage can be neglected,the final penetration depth considering projectile shank friction can be integrated from Newton's second law of motion as

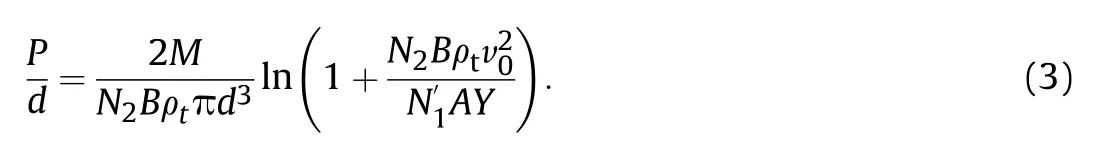
where

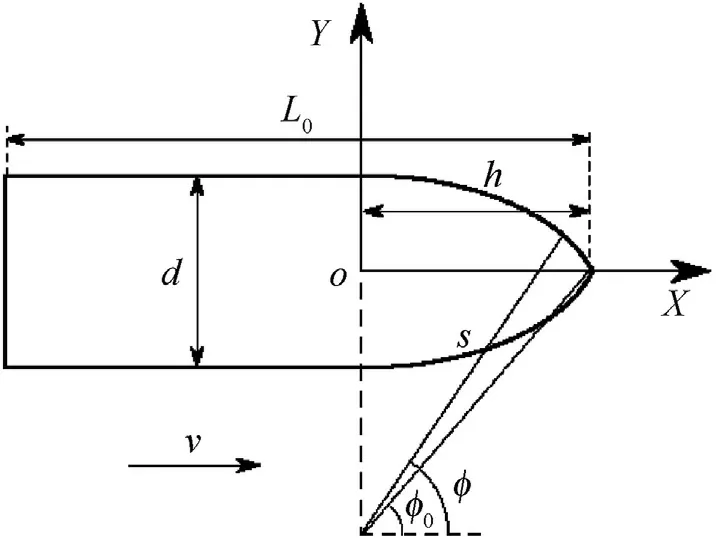
Fig.1.Schematic of a projectile.

where caliber-radius-head(CRH)，v0is the initial impact velocity of projectile.

Taking

while I*＜1,Taylor series expression of Eq.(3)gives

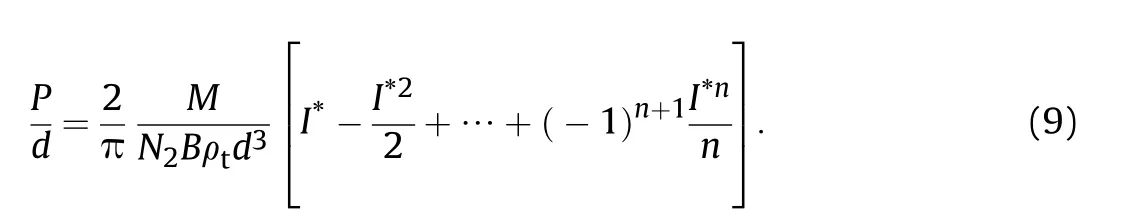
Let

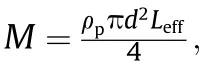
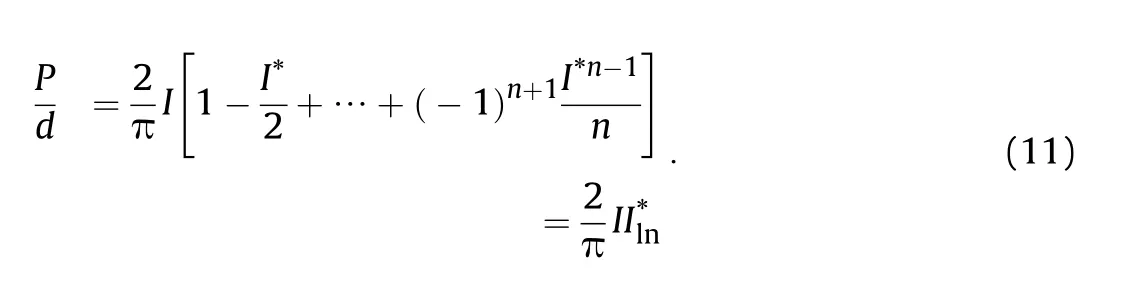
Then,the 1st-order approximation of Taylor series expression of Eq.(3)is Although Eq.(12)has the same appearance as the corresponding Eq.(20)in Ref.[4],in Eq.(4)contains an extra term of friction contribution from the projectile shank in comparison with N1in Eq.(8)in Ref.[4].

For the penetration of concrete target,where the unconfined compressive strengthis measured in MPa.For the penetration of aluminium-alloy target,as suggested in Ref.[8],where E and Y are the elastic modulus and yield stress of aluminium-alloy target,respectively.

According to Eq.(11),the 1st-order approximation of Taylor series expression of Eq.(3),where μ=0,is

It was shown in Ref.[4]that empirical formula

has better agreement with deep penetration testing data than Eq[14].

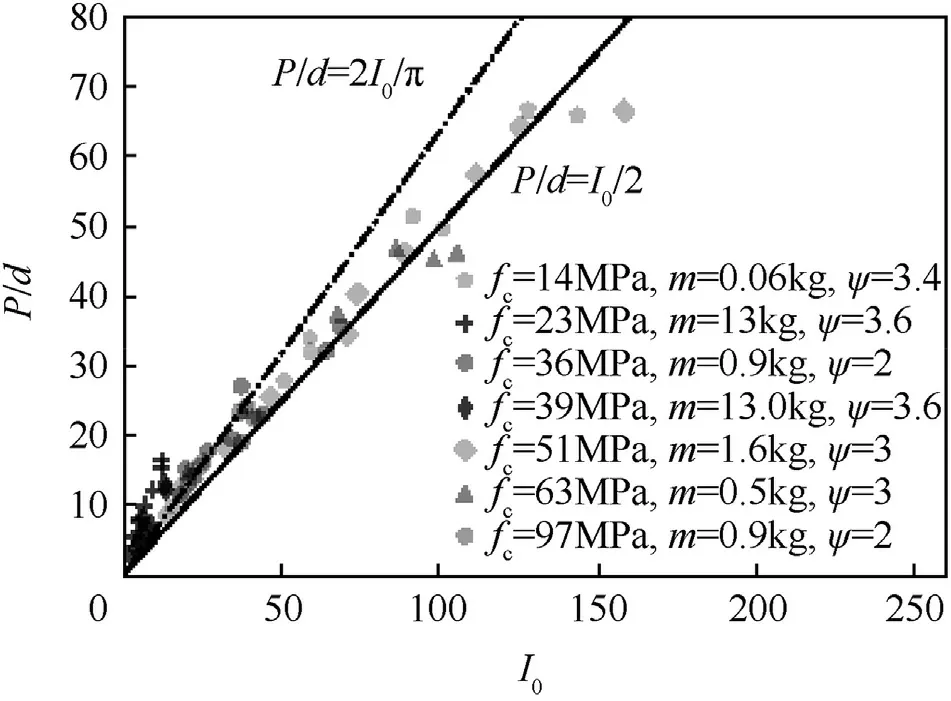
Fig.2.The comparison between non-dimensional penetration depth P/d of experiments and formulas of P/d=2I0/π and P/d=I0/2[5,9,10]

3. Rigid-body penetration of concrete

The comparison of Eq.(14)and Eq.(15)with experimental data of penetration of concrete target is shown in Fig.2.It is shown that empirical formula P/d=I0/2 fits much better than the analytical formula P/d=2I0/π in full-range experimental data, and the deeper the penetration is,the better the empirical formula is.In order to measure the predictability of Eq.(14)and Eq.(15),the difference ratio between experimental penetration depth Pexpand that from predicting formula Ppreis defined as

Fig.3 shows the dependence of R on I0for Eq.(14)and Eq.(15).Fig.3(a)shows the variation of the difference ratio R with I0for the analytical formula P/d=2I0/π.Fig.3(b)shows the variation of the difference ratio R with I0for the empirical formula P/d=I0/2.When I0≥30,it is evident that the difference ratio for P/d=2I0/π has different trend from that for P/d=I0/2.The former increases with I0while the latter decreases with I0,reflecting the importance of frictional force on the projectile shank increases with the increase of penetration depth.When I0＜30,which corresponds to P ＜15d,the entrance effects become important,which is not the focus of this study.

Taking friction into account,would no longer equal to unity,and Eq.(12)can be transformed into

The complexity of friction makes the calculation of frictional coefficient from first principles impractical and necessitates the use of empirical methods. Lim et al. analysed a large number of experimental data on the variations of frictional coefficient in sliding of steel on steel in a wide range of sliding conditions and presented the results of the analysis in the form of a friction regime map,and showed that at very high loads and velocities,a layer of molten metal forms between the sliding surfaces,reducing frictional coefficient to very low values[11].Balakin took frictional coefficient as the product of pressure and sliding velocity and showed that the frictional coefficient would decrease with the increase of this product.It is shown that frictional coefficient would decrease to lower than 0.02 when the product of pressure and sliding velocity was higher than 7GPa·m⋅s-1,and a declining trend was shown with the increase of this product[12],though being out of the experimental data limits,where the penetrating pressure and velocity can up to GPa and hundreds of meters per second,respectively.To the best of our knowledge,the precise frictional coefficient under high velocity penetration was not found,considering all the afore facts,an approximative coefficient lower than 0.02 was preferred in this article.

Fig. 3.Difference ratio of experimental and predicting penetration depths from formulas.

Fig.4.Schematics of friction experimental projectiles.

In order to investigate the effects of friction on projectile shank,Ref.[2]conducted a series of penetration experiments with normal ogival head and normal shank and ogival head but reduced-shank projectiles.All projectiles have the same mass and head geometry,with a caliber-radius-head(CRH)of 3 and head radius s of 45 mm.Projectiles are shown in Fig.4.Concrete targets are 550 mm in diameter while the compressive strength is 45 MPa using 150 mm cubic samples.Experimental results are shown in Table 1.

It is shown that the experimental penetration depths of normal shank projectile are consistently between 630 and 640 mm,which implies that experimental results are reliable.On the other hand,the penetration depths of reduced-shank projectiles are larger than those for normal shank projectiles. The penetration depth of reduced-shank projectiles under normal penetration should be larger than the experimental results since the trajectory deviation occurred in experiments,which increased the penetration resistance due to the unsymmetrical pressure distribution.Since their head geometries are same,it was suggested that the increase of the penetration depth was due to the disappearance of the friction resistance on the projectile shank.The ratio of the penetration depth increase,compared with normal shank projectiles,were 7.1%and 14.3%,respectively,with an average value of 10.7%.This increase was caused only by the elimination of shank friction while the head friction was still effective,and was in accordance with the simulation research,which stated that ignoring friction of projectile shank for deep penetration into concrete target would deduce at least an error of 10%[13].

In fact,this results from experiments can further supported from some evaluations about Eq. (9). The meaning ofis comprehensive and complex,for it consists of penetrator head shape ψ,friction,nominal penetrator length L0,initial impact velocity v0,etc.For most concerned velocities(v0＜1200m⋅s-1)and penetrator head shapes(0.5 ＜CRH ＜6),I*can be calculated in advance and only ranges from 0 to 1 and the corresponding

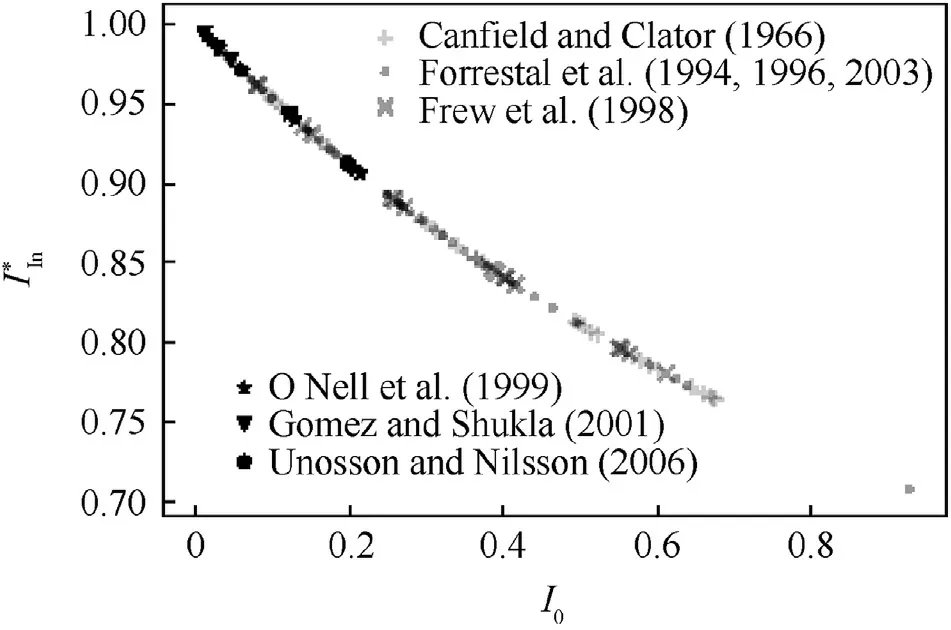
Fig.5.The relations between and I*within concerned velocities and penetrator shapes.

ranges from 1 to 0.7,as shown in Fig.5.If the median is taken rashly as 0.85 to represent the concernedvalues(0.95—0.75),the error rate would be just around 10%.In other words,even simply taking a certain value to represent all the concernedvalues,the largest error rate is around 10%,which would be immersed in the engineering experimental error and is acceptable in engineering.Together with the friction resistance contribution,the implicit effects of parameters included inand friction would account for a resistance portion as much as 0.235=1-0.9×0.85,and this portion is just around the resistance difference between penetration resistance considering and not considering friction(≈0.215)(The comprehensive effects ofwas crossed out by the division,depicted by coefficients 2/π and 1/2 in Eq.(14)and Eq.(15)).Even though the detailed distribution of dynamic frictional coefficient is unclear,it is more likely that the overall friction resistance accounts for a proportion of around 10%in total penetration resistance,and the detail needs further supports from experimental or theoretical study.

4. Rigid body penetration of aluminium target

Forrestal et al.[14]proposed a formula to predict the penetration depth of aluminium-alloy target,i.e.,

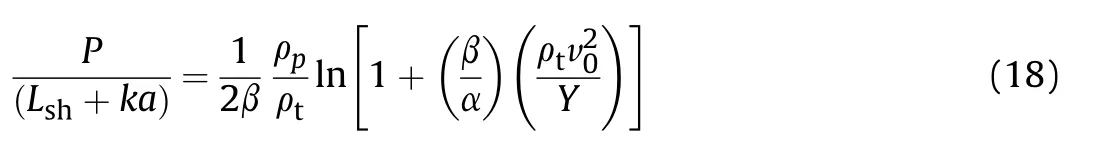
where

Table 1 Penetration results with and without shank friction.The experiments labeled with asterisk*deviated from initial projectile axis with a‘J’shaped trajectory in the end part.Their penetration depths were measured alongside the curved trajectories.

According to Eq.(19),Lsh+ka is the effective length of projectile Leff,and Eq.(18)is actually the same as Eq.[3].when shank friction is ignored.The shank friction was neglected due to the experimental observation of a 5—15μm melting layer normal to the tunnel surface[3,15].The penetration depth into aluminium-alloy target without and with considering friction can be determined by Eq.(14).and Eq.(15)[4].

A series of penetration experiments on aluminium-alloy targets,6061-T651 and 7075-T651,using projectiles with CRH of 0.5 and 3 and materials of C300,T200,VAR4340,AerMet100 were reported[3,14,16—18].Fig.6 shows the variations of P/d with I0,where experimental data with excessive head erosion(more than 10%)was ignored.It is shown that the higher the strength of projectile is,the better the prediction of P/d=I0/2 will be.This is because high strength projectile can meet rigid-body projectile assumption.It is shown that the relations between P/d and I0for various projectile head geometries and materials are still in good agreement with P/d=I0/2,even though they are different remarkably in head geometry,diameter and mass.It is worth noting that experimental data fits better with P/d=I0/2 than P/d=2I0/π,which indicates that the friction on projectile shank cannot be ignored.However,P/d=I0/2 slightly underpredicts the experimental results,especially at higher impact speeds.Since P/d=I0/2 is derived empirically with an overall shank friction coefficient assumption of μ=0.01,this suggests that the friction coefficient on the interface of steel projectile and aluminium alloy is less than 0.01 for high speed penetration.Even this frictional coefficient is relatively small,the friction is not negligible because of the relative large effecting area on the shank,which would account for more obvious proportion of penetration resistance in deep penetration cases.Since the shank pressure distributes unevenly,this coefficient decrease is more likely caused by the melting layer in the former part of the shank.

According to the model for metal perforation without plug formation proposed by Recht and Ipson[19]that all kinetic energy loss is through plastic deformation of the target Wt:

Fig.6.Variations of non-dimensional penetration depth with I0 according to experimental data and analytical and empirical formulas of P/d=2I0/π and P/d=I0/2 for aluminium-alloy targets.

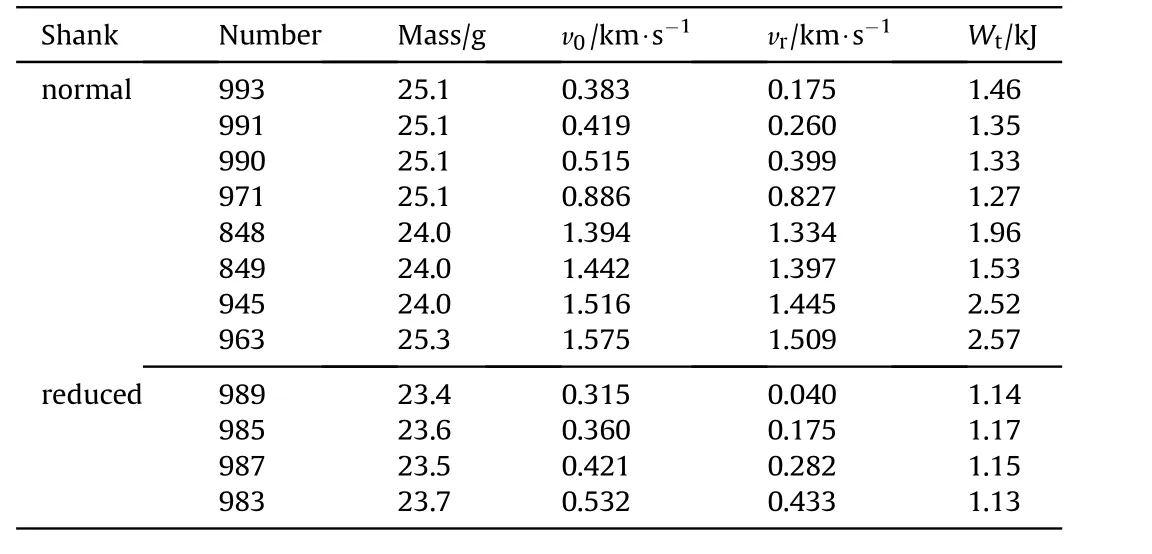
Table 2 Perforation data summary of 25.4 mm thick 6061-T6 aluminium plates for projectiles with normal and reduced shanks.

where vris the residual velocity of projectile.

A series of perforation experiments of aluminium-alloy target using conical head projectiles with normal shank and reduced shank projectiles were reported in Ref.[1],where the reducedshank projectiles were introduced to avoid shank drag.The results are shown in Table 2,in which shot numbers 849 and 945 with T-200 projectiles showed blunting of the conical head tips according to post-perforation shadowgraphs;whereas,shot number 848,with a slightly lower impact velocity,and shot number 963 with a C-300 maraging steel projectile showed no permanent head tip deformation.

As shown in Table 2, in the same velocity range(v0＜0.886km⋅s-1), where v0＜0.886km⋅s-1for normal shank projectiles and v0＜0.532km⋅s-1for reduced shank projectiles,the plastic deformation energy Wtof projectiles with reduced shanks are less than those with normal shanks in the same perforation process,which is obviously caused by the elimination of shank friction.This again supports the conclusion that the shank friction influence should be considered in the penetration and perforation analysis.

Furthermore,Wtdecreases slightly with the increase of impact velocities for normal-shank and reduced-shank projectiles,respectively.This phenomenon is attributed to the reduction of frictional coefficient on projectile caused by the melting layer on the interface,proposed by Forreastal et al.[3],and the little varying effect of inertia term in resistance when the velocity under a threshold,proposed by Rosenberg and Dekel[8].However,as shown in Table 2,when the impact velocity is greater than the threshold,the effect of inertia term or blunting would become obvious.

5. Conclusions

This article studies the friction effect on rigid-body penetration.Based on the penetration resistance considering shank friction and available experimental results,the friction effect on rigid-body penetration into concrete and aluminium-alloy targets are discussed.Main conclusions are.

1.For deep penetration of concrete target,the friction on the shank cannot be ignored,and the overall friction resistance accounts for a proportion of around 10%in total penetration resistance.The experimental fitting of empirical formula P/d=I0/2 is better than the 1st-order approximation of analytical formula,P/d=2I0/π,shown in Ref.[4],is clarified by the inclusion of shank friction and the effects of comprehensive quantity I*lnin the former formula.

2.For penetration of aluminium-alloy target,the friction on the shank has a similar effect as that for penetration in concrete,and cannot be ignored either.The difference between penetration in concrete and aluminium-alloy targets is that with the increase of penetration depth or impact velocity,the friction coefficient on the projectile into aluminium-alloy target would decrease because of the formation of melting layer on the interface between the projectile and aluminium-alloy target. In other words,the penetration friction resistance would decrease with the increase of penetration depth or impact velocity for aluminium-alloy targets.

Acknowledgments

The first author would like to acknowledge the scholarship granted by the China Scholarship Council and the support from the Institute of Chemical Materials,CAEP.