一种新型的半导体SMA缺陷识别方法
2019-10-30胡佳美吴锡生
胡佳美 吴锡生
(江南大学物联网工程学院,无锡,214122)
引 言
半导体电子器件在家电、电表、照明、安防和充电桩等多个领域都有着广泛的应用,对元器件封装起着安装、固定、密封和保护元器件电气性能等方面的作用。电子元器件封装体若出现缺陷,将影响到元器件的性能,因此在生产过程中对其封装体进行缺陷检测就变得十分必要。表面贴装工程(Surface mount assembly,SMA)是封装技术中的一种,相比其他封装技术有高密度、低成本、小体积和生产自动化等特点,研究SMA封装元器件的缺陷检测方法,是生产高质量元器件产品的迫切需要。随着计算机技术和图像识别技术的发展,机器视觉被应用于封装技术缺陷检测中,这不仅可以降低劳动力强度,还能排除主观因素的干扰,提高检测精度。
传统机器视觉的缺陷检测手段,主要是通过对检测目标进行分割,然后通过人工进行缺陷特征的选取和描述,最后通过数字图像处理(二值化、边缘检测和模板匹配等)的方法对图像进行检测。如Wang等[1]提出了一种多图像减法检测发光二极管屏像素缺陷的方法。董先飞等[2]通过边缘检测算法提取塑封边缘,结合差影法和模板匹配法检测表面质量缺陷。以上数字图像处理方法的效果,往往依赖于研究人员长期积累的经验,模板匹配法还受限于所选取的模板图片,泛化性能较低。随后,人工神经网络开始广泛运用到缺陷检测中。如沈凌云等[3]提出主成分分析法(Principal component analysis,PCA)和径向基神经网络相结合电池缺陷检测方法。高向东等[4]提出了主成分分析-误差反向传播神经网络(PCA-back propagation,PCA-BP)分类模型识别焊件表面缺陷的方法。熊忠阳等[5]提出将粒子群优化算法和BP神经网络结合并应用在变压器故障检测中。周宣汝[6]提出一种基于HOG特征和支持向量机(Support vector machine,SVM)的交通信号灯实时识别算法。SVM和人工神经网络等方法相对于传统图像处理方法有一定的自适应性,但仍需要依赖大量先验知识,人工干预多,当检测目标改变或者检测内容复杂度提高时,将会面临更大挑战,而且使用PCA对图像进行提取会破坏图像的二维结构而导致精度下降。近年来,随着大数据和云计算的发展,深度学习成为人们研究的热点,开始被尝试应用于各个行业。如Allam等[7]采用循环神经网络(Recurrent neural network,RNN)和前馈神经网络相结合建立糖尿病患者葡萄糖调节预测控制模型。文献[8]运用深度置信网络(Deep belief network,DBN)对涡轮风扇发动机引擎组件进行故障诊断。这些深度学习算法虽取得了不错的识别效果,但网络的泛化性能较低,也不能满足缺陷多样的二极管表面缺陷的检测精度。
为此本文提出将双向二维主成分分析法(Bilateral two-dimensional principal component analysis,Bi-2DPCA)和改进的AlexNet网络相结合的二极管表面SMA封装缺陷识别方法。先用Bi-2DPCA提取的主要特征作为网络的输入,然后使用正态随机池化(Normal-Stochastic Pooling)对卷积产生的特征数据进行下采样操作,最后在全连接层引入DropConnect来提高泛化性能,实验结果表明改进模型能很好地提高产品缺陷的识别率,并有较好的泛化性能。
1 相关理论及AlexNet模型
1.12DPCA算法
二维主成分分析法(Two-dimensional principal component analysis,2DPCA)是 Yang等[9]提出来的一种直接图像投影技术。相比与PCA算法,2DPCA不需要将图像矩阵展开成一维向量,图像的协方差矩阵可以通过二维图像矩阵直接构造出来,从而保留图像的二维信息。假设样本集中有N个m×n的图像S={S1,S2,S3,…,SN},X为n维列向量,

通过式(1)将S投影到X上得到投影向量Y,2DPCA最终目的为求得一组坐标轴使得投影样本的全局散度最大,即使得J(X)最大为

式中:GX表示训练样本图像的散度矩阵,tr(GX)为散度矩阵GX的迹。所以有

式中:G=E[(S-ES)T(S-ES)]=表示第i类中第j个图像矩阵表示第Ti类样本的平均样本。获取J(X)极大值的前d(d<n)个最大特征值λι,可以用累计特征贡献率式(4)循环求解获得。

式中:λ1≥λ2≥…≥λn是G的n个特征值,α表示特征累计贡献率,d表示前d个最大特征值对应的特征矩阵记为X=(X1,X2,…,Xd)。
1.2 Bi-2DPCA算法
2DPCA中的变换只提取了数据矩阵行内的特征,而Bi-2D PCA算法则在2DPCA算法基础上增加对列内进行特征变换,以此达到对二维图像在两个维度上同时对图像长宽进行压缩和特征提取的目的。对列特征变换过程与2DPCA类似,对应的对式(1)中的Y进行行内2DPCA变换,得到一组基Z,则图像进行Bi-2DPCA变换可表示为

式中:R表示经过行列双向投影的特征矩阵。列变换中投影维度数由式(4)同理求出。
1.3 正态分布原理
正态分布又叫高斯分布,对于随机变量X,其概率密度函数满足式(6),其中μ表示数学期望,σ2表示方差。随机变量的信息熵指随机变量不确定的程度,在数学期望和方差一定的条件下,高斯分布随机变量具有最大信息熵[10]。

1.4 AlexNet模型结构
AlexNet模型[11]是Krizhevsky和Hinton小组在ISVRC2012大赛中使用的卷积神经网络[12]模型,与传统神经网络相比,它不需要人工提取图像特征。AlexNet模型一共包含5个卷积层和3个全连接层。其中,每个卷积层后都紧接着将卷积得到的特征矩输入到激活函数Relu中,第1层和第2层卷积层中对从激活函数输出的特征进行局部响应归一化(Local response normalization,LRN)处理,在第1层、第2层和第5层卷积层中对特征矩阵做下采样处理,第1层和第2层全连接层中采用Dropout,本文训练样本与原AlexNet训练样本的维度有所不同,根据实验效果,对网络模型配置同比修改,修改后的AlexNet网络模型配置如图1所示。
AlexNet网络模型中使用了LRN,即图1中的Norm层,LRN是受生物学上活跃的神经元对周边神经元的侧抑制现象的启发,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,从而增强模型的泛化能力,其计算为
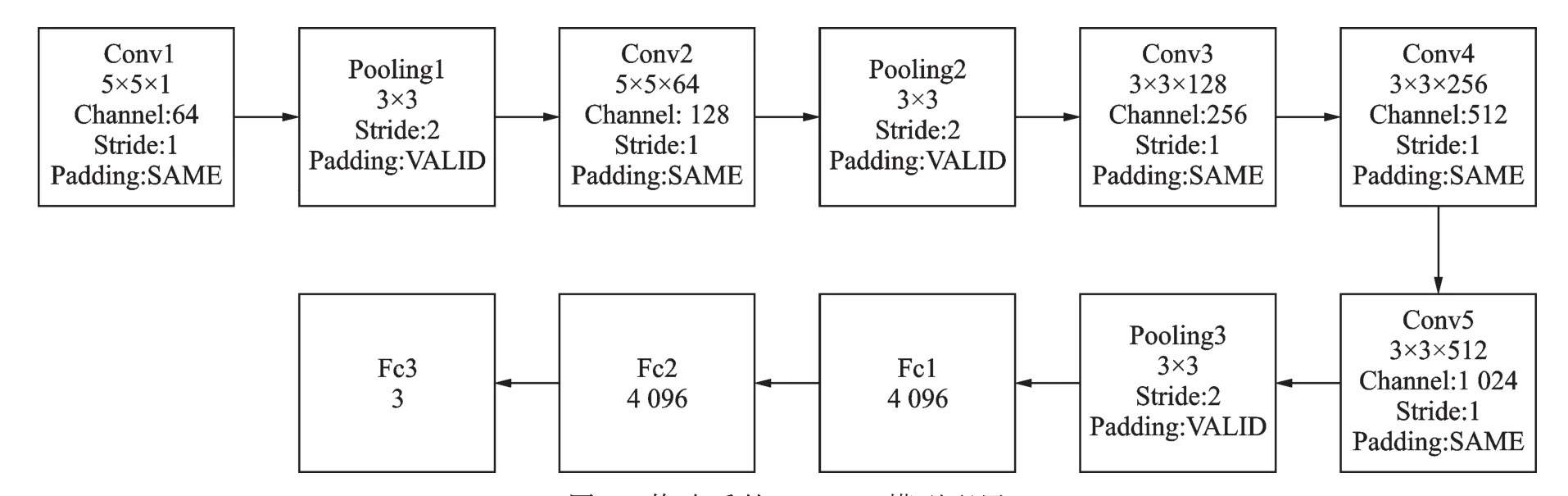
图1 修改后的AlexNet模型配置Fig.1 Modified AlexNet model configuration

池化层(Pooling Layer)的存在主要是为了降低特征的维度并保留主要信息,一定程度上避免过拟合,保持模型旋转、平移和伸缩不变形。池化过程也称为下采样,跟卷积过程有点类似,用一个采样核在输入的特征矩上从左上角开始滑动,运用某种规则在采样核范围内求超参数,然后将结果输入到网络的下一层,整个采样过程不涉及到参数的训练。常用的池化方法有均值池化(Mean pooling)和最大值池化(Max pooling)。
2 基于Bi-2DPCA和AlexNet的二极管塑封缺陷检测方法
二极管塑封表面缺陷形态具有多样性和不可预测性,本文算法除了提高缺陷识别精度外,还着重提高检测模型的泛化性能。一般来说,模型在测试集上的测试精度越接近训练集上的精度,就认为该模型具有比较好的泛化性。本文算法首先由训练样本生成虚拟样本,再将生成的样本用Bi-2DPCA算法对做降维处理,然后输入到改进的AlexNet模型中进行训练,建立缺陷识别模型,测试集先通过降维变换矩阵进行降维再输入模型进行缺陷识别分类,输出识别结果,流程如图2所示。

图2 算法流程Fig.2 Algorithm flow
2.1 样本数据扩充
训练样本分布不均衡或者训练集方差小容易使训练出来的卷积神经网络模型欠拟合或者过拟合,从而导致模型在测试集甚至是在训练集上识别效果欠佳。本文收集到的无材料图像尤为不足,为了克服样本分布不均衡的问题,本文算法在所收集图像基础上进行水平和垂直反射变换、灰度变换操作等生成虚拟样本。数据样本扩充处理如图3所示,其中a组是二极管SMA封装体良品图像,b组是槽体中无材料图像,c组是材料崩角的缺陷图像,d组是表面印字不清缺陷图像,每组图的第1张为原图,后面3张分别是由水平反射变换、垂直反射变换和灰度变换处理而来。生产过程中可能会遇到材料槽中无材料的情况,这种情况下需要识别出来作特殊处理,所以将没有材料的情况也当作一类缺陷进行识别。

图3 样本数据图像扩充Fig.3 Image expansion of sample data
2.2 样本数据的Bi-2DPCA降维处理
对输入数据的特征提取是AlexNet模型进行识别的关键,也是难点部分。本文使用图像的规格为256×128,维度为 32768,若直接从原图像进行特征提取维度会很高,使得整个网络的计算复杂度高,冗余的特征也会带来一些噪声,降低网络识别性能,因而考虑在正式训练网络前,对数据样本先进行降维操作。使用PCA降维步骤:(1)每张训练图像Si转化为一维列向量列向量组成矩阵;(2)计算矩阵协方差矩阵,求其特征值和特征向量;(3)根据所给的特征贡献占比确定特征维度,组成特征转换矩阵;(4)用特征转换矩阵对图像进行重构,最后将重构图像输入AlexNet网络。由于使用PCA将图像展开成一维,破坏了图像二维结构,影响图像特征表征能力,且针对所有样本组成的庞大的协方差矩阵求特征值和特征矩阵计算量大、耗时,所以本文使用Bi2DPCA进行降维,Bi2DPCA进行降维步骤:(1)每张训练图像Si根据式(3)求出行方向协方差矩阵;(2)求出特征值、特征向量,根据式(4)迭代求出维度数,重构图像;(3)将重构后图像根据式(5)求出列方向协方差矩阵;(4)求出特征转换矩阵重构出图像输入AlexNet网络进一步提取特征。
2.3 正态随机下采样
针对原AlexNet网络模型中使用最大值池化(Max pooling)只能保留最强信号易忽略有效特征的不足,提出正态随机池化(Normal-stochastic pooling)。正态分布是随机分布中信息熵最大的分布,将原随机下采样中的均匀分布概率采样改进为正态分布概率采样,这样可以表示一种多模态激活,除了让最大值的激活元素被取到外,同时也有可能取到其他某些非最大激活,这样可以增强原随机采样的信息熵,提高其随机性,从而增强模型适应性。而原Max-Pooling只能捕捉到网络中最强的激活,所以其泛化性能相对较弱。本文算法具体做法是设池化窗口大小为3×3,在池化窗口内将上一层的特征Map内每个元素值除以和,得到每个元素占比,再通过正态分布产生权值系数,与每个元素的占比相乘,得到一个新的取值概率,其计算如式(8)所示,示意如图4所示。

式中:Pij表示取采样区域元素的概率;Vij表示采样区域元素值;sij表示正态分布随机系数;m,n代表采样区域的行和列。
2.4 采用Dropconnect的全连接层
在AlexNet模型的全连接层部分,其前两层中加入Dropout操作,如图 5(a)所示,Dropout通过随机丢弃某些神经元节点,使对应的神经元失效停止工作,当网络进行反向传播更新权值时,就不再更新与该节点相连的权值。图5中V1,V2,V3,V4代表连接层输入,m(.)代表一个由0和1一定概率的行向量。

图4 正态随机池化过程Fig.4 Normal-stochastic pooling process

图5 Dropout与 Dropconnect处理Fig.5 Dropout and Dropconnect process
本文在AlexNet的全连接层中使用Dropconnect[13]来对特征进行稀疏化。Dropconnect和Dropout都是对全连接层进行稀疏化,但与Dropout不同的是,Dropconnect不是随机将激活函数节点的输出设为0,而是将节点中每个与其相连的输入权值以1-p的概率置为0,如图5(b)所示,计算公式为

式中:v为n×1维的连接层输入;W为d×n维的权重矩阵;M为1×d的行向量;a(x)为激励函数,*表示对应元素相乘。从图5(a)可以看出,Dropout每断开一个节点,就意味着把与该节点相连的所有输入权值全部影响价值都舍弃。这样做虽然在一定程度上对特征进行了稀疏,但是由于网络输入前已经作了Bi2DPCA主成分提取,输入网络的特征都是比较关键的特征,因而采用Dropout容易使得某一些关键特征被整个舍弃,导致识别效果不佳。而Dropconnect则是在权值层进行稀疏,不会使某个特征的权值整个都取零,这样既能够保留所有的主要特征,又能对每个特征进行稀疏,从而能够在提高识别率的同时有较好的泛化性。
3 实验结果与分析
3.1 实验平台与数据
实验在Window10操作系统(Intel i5-7600 CPU、8 GB内存)上运行,基于Pycharm平台使用Python3.6语言,在谷歌的TensorFlow1.7.0框架下对二极管封装体表面缺陷进行识别分类。
实验所使用的数据集是从扬州某科技股份有限公司生产线上得到的二极管SMA图片。相机是日本Sentech公司型号为STC-MB232PCL的CCD工业相机,TAMROM的1A1HB镜头,光源使用SAKAZUME的LED光源。CCD工业相机快门时间非常短,图像畸变小、灵敏度高且噪声低,而且其输出的是裸数据,比较适合进行高质量的图像处理算法,如机器学习等。实验将样本数据分为良品、缺陷品和无材料3种进行识别。经数据扩充后,共有10128张良品数据、2000张缺陷数据和550张无材料数据,在3类数据中随机各取30%作为测试集,10%作为验证集,剩余样本参与模型训练,相同的实验做10次,并将实验精度在各迭代周期上取平均值作为最终结果,以此避免偶然因素的影响,更好地展现实验结果的普遍性。另外,为了检测本文算法的泛化性能,实验在Mnist数据集和Cifar10数据集上作识别对比。Mnist数据集和Cifar10数据集部分样本图像如图6所示。
3.2 实验步骤及参数
本文算法主要分为4个步骤:建立数据集、构建网络模型、训练模型参数和测试数据。实验分别对训练集和测试集数据进行主成分提取,然后用训练集训练模型,将训练好的模型对测试集进行测试。经过多次试验调整参数,为提高收敛速度,最终确定模型所涉及到的超参数如表1所示。

图6 实验所用数据集Fig.6 Data set of experiment

表1 实验超参数Tab.1 Experimental super parameters
为了寻找最佳迭代次数,实验每迭代200次就测试识别精度,结果如图7所示,从图7中可以看出,迭代到3800次左右模型基本收敛。

图7 迭代次数与精度关系Fig.7 Relation between iteration number and accuracy
为了考察特征维度与识别精度的关系,找到最佳特征维度,实验先对图像列方向进行2DPCA特征维度改变与识别率关系,确定行方向最佳特征维度后,再对图像列方向上改变特征投影维度,考察模型的识别效果,实验结果如表2所示。
从表2的行方向识别率可以看出,当仅在行方向做2DPCA时,特征维度较少时,识别率随着维度增加提高的速度较快,但维度增加到35后,识别率变化很小,所以实验确定行方向上投影维度为35。再在列方向上作2DPCA(即Bi-2DPCA)改变列方向上维度,从表2列方向识别率可以看出列特征维度较少时,识别率同样随着维度增加提高较快,但列维度较低时,模型作Bi-2DPCA降维处理的识别率低于只对样本作行方向2DPCA处理的识别率,当维度数为45时,识别率基本保持稳定。综上所述,行方向上投影维度数为35,列方向上投影维度数45左右最为合适。
3.3 实验结果及分析
本文算法与其他相关算法在扩充后的数据集上实验结果统计如表3所示。从表3中可以看到,本文算法识别精度最高,在3个深度神经网络中,训练时间5.4 h相对来说时间较短,由于本文算法对AlexNet模型在池化层和全连接层进行稀疏化改进,所以本文算法在收敛速度上慢于Bi-2DPCA+AlexNet算法。但测试时间是4个算法中最短的,SVM的训练时间明显少于其他3个深度神经网络,但是测试时间比其他算法要长。考虑到在生产线上进行实时检测对算法的测试时间要求较高,而训练时间要求并不是太苛刻,因此,从实用性角度来看,本文算法更加适合二极管塑封表面流水线的质量检测。

表2 特征空间维度与识别率关系Tab.2 Relation between characteristic dimension and precision

表3 本文算法与其他算法对比Tab.3 Comparisons between the proposed algorithm and other algorithms
为了验证本文算法在泛化性能上较原算法有所提升,实验使用PCA+AlexNet算法、2DPCA+AlexNet算法和本文所提算法应用在Mnist手写数据集以及Cifar10数据集上进行识别实验,并通过算法在测试集与训练集上的错误率的差值即方差来对上述3种算法的泛化性能进行对比。从图8中可以看出,在Mnist数据集上,2DPCA+AlexNet算法的方差最小,即在测试集上的识别率最接近训练集,本文算法在Mnist数据集方差略高,泛化性能比2DPCA+AlexNet算法稍差一点。图9是在Cifar10数据集上的实验结果,结果显示本文算法方差为0.81%,在3个算法中最低。从上述实验结果分析,可能是因为Mnist数据每张图片是简单的黑白二值化图像,进行过度的降维特征提取,会导致有用的特征丢失影响识别结果,模型不需要有太强的泛化性就可以达到比较好的识别效果。相比之下,Cifar10中的图像场景更加复杂,所以泛化性强的模型在Cifar10测试集上的优势更能显现。
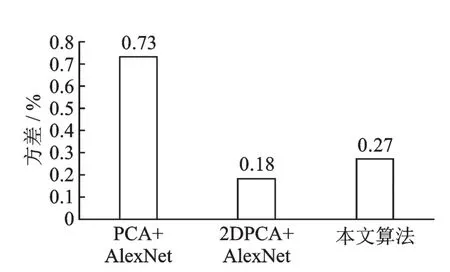
图8 Mnist数据集泛化性能对比Fig.8 Generalization performance comparison of Mnist data set
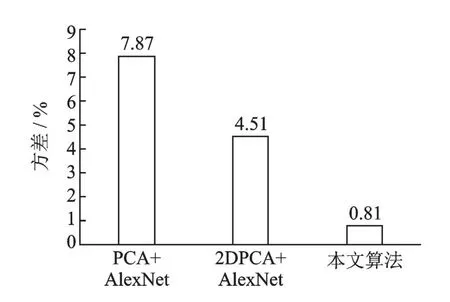
图9 Cifar10数据集泛化性能对比Fig.9 Generalization performance comparison of Cifar10 data set
最后,将上述3种方法应用在扩充后的二极管塑封表面图像集上,进行泛化性能对比。结果如图10所示,本文提出的算法方差为2%,在测试集上识别率最接近训练集。可见,本文提出的算法在二极管塑封表面图像集上可以有效提高模型的泛化性,有更好的适应性,并且在复杂特征的图像集上有很好的鲁棒性。
4 结束语
本文提出了一种新型的半导体SMA缺陷识别方法,可以对二极管封装表面缺陷图像进行很好的识别,使用Bi-2DPCA降维既可以保持图像二维结构提取主成分,又可以降低计算复杂度,缩短计算时间。在AlexNet结构基础上,提出正态随机池化方法进行下采样并引入Dropconnect稀疏,实验在SMA封装表面数据集、Mnist数据集和Cifar10数据集都上有很好的泛化性能,并且在SMA封装表面数据集有很好的识别率,这对于提高二极管制造过程中的良品率有十分重要的意义。后续的研究主要是考虑如何进一步提高识别精度以及优化模型结构以提高训练的收敛速度,使得本文算法可以更好地应用到半导体行业的其他元器件识别生产过程中。

图10 二极管塑封表面数据集泛化性能对比Fig.10 Generalization performance comparison of plastic sealing surface of diode data set
