一种抵抗零中频接收机正交失配特性的FM解调算法
2019-10-30刘宁
刘 宁
(中国西南电子技术研究所,成都,610036)
引 言
过去30年,无线通信得到了快速的发展与不断的演进。无论是在军事通信领域,还是在民用领域,无线通信都有了长足的进步,在各频段上都发展出了新的模式,给人们的生活带来了越来越多的便利[1]。无线通信系统在功能、模式等方面正逐渐朝着多样化的方向发展,更有效地满足不同层次的通信需求。特别是在硬件体系结构上,取得了重大的富有成效的进展。
零中频接收机最早出现在20世纪30年代,替代已广泛应用的超外差接收机。零中频接收机又称直接变频接收机,其典型结构如图1所示。与超外差结构相比,零中频接收机结构只需一次混频,直接将射频信号的中心频率下变频至零中频。信号从射频直接搬移到了零中频,省去了中频变换这一级,这样接收机中的器件数量减少,系统的体积相应变小,成本下降,目前零中频结构已成为宽窄带通信中射频前端一个广泛应用的解决方案[2]。
零中频结构采用正交下变频方式,本振需产生相位相差90°且增益一致的两路正交本振信号。而在实际硬件电路中,由于器件的物理特性、电路板传输特性及工作环境的影响,零中频接收机会产生正交失配的现象,即两路正交本振信号无法做到相位完全正交、增益完全相同。正交失配会在基带产生关于零频对称的有用信号和镜像信号的叠加,引起接收基带信号失真,最终影响解调后信号质量[3,4]。
为了有效抵抗模拟域正交失配的影响,一般有以下两种方法进行补偿或校准[5-7]:(1)离线测试、在线校正法。即在实验室,利用信号源灌入射频接收输入端,在数字域先计算出幅度的不一致和相位不正交的具体数值,然后在实际工作中,利用离线测试的结果进行校正。(2)闭环自适应校正法。即在发射通路与接收通路中存在一个射频开关,能够将发射信号直接灌入接收端,由于完全获得发射端发射的信号,则可以在接收端利用发射信号与接收信号进行延迟匹配后进行建模,并解算出相应参数进行正交失配的补偿。
以上两种方法,从目前的实践来说,本质上是都是建模,训练,算法较为复杂。方法(1)完全不具备实时跟踪特性。每套硬件的正交失配特性不完全相同,同时随着工作环境的变化,正交失配的特性会随之缓慢变化,导致离线测试的结果与实际工作的状态不一致,性能恶化。方法(2)需要额外附加新的硬件电路,每次测算,都需要更改硬件开关状态,直接将发射端接连到接收端,严重干扰正常通信,并且开关状态的不同同样会引起射频电路匹配性能的不同,导致建模不准确。
FM作为角度调制的典型方法,由于其优秀的抗干扰能力,广泛应用于长距离、高质量的通信系统中,如空间卫星通信、超短波电台和调频立体声广播等[8]。随着射频零中频接收机结构的成熟,在FM广泛应用的超外差结构也逐步向零中频结构转换,正交失配成了FM调制通信系统中不可忽略的问题。
本文提出的鉴频算法即是利用FM调制信号的特点,在FM鉴频过程中实现对射频正交失配的抵消,鉴频后信号质量完全不受正交失配特性的影响。其算法简单易行,不需要复杂的建模及模型参数解算,不需要训练过程,且具备完全实施跟踪特性。
1 鉴频算法设计
理想调频信号在射频域的表示为

式中:wc为载波频率,θ(t)=2πk∫m(t)dt,m(t)为被调信号,k为频率敏感度。
显然其理想的基带的表示为

当然也可将Q(t)表示为Q(t)=-sin(θ(t))进行推导,两者都不失一般性。
式(2,3)导数可表示为

当射频电路正交下混频存在正交失配的情况下,失真的基带调频信号可表示为

式中:A表示由于正交失配带来的I、Q两路幅度不一致性,φ表示由于正交失配带来的I、Q两路正交相位的偏差。由式(2,3)代入式(6,7),则可得到

对于理想信号的反正切解调

不考虑信号的线性变化,则被调信号m(t)=θ(t)',当考虑硬件的正交失配情况下的反正切解调时,将失真的基带信号,即式(8,9)代入式(10)可得

由式(11),正交失配的相位不正交和幅度不一致使得反正切解调信号产生了失真,并且失真并不是单纯的线性放大或缩小。假定一信号p(t),令p(t)=Iˆ(t)Qˆ(t)'-Qˆ(t)Iˆ(t)',将式(8,9)代入p(t)的表达式,则

显然,通过移项,能得到关于被调信号m(t)的表达式为

A表示由于正交失配带来的I,Q两路幅度不一致性,φ表示由于正交失配带来的I、Q两路相位正交性的不一致。对于解调后的信号m(t),A与φ在式中只起线性作用,且实际工作过程中,正交失配程度较小且是一个缓变化过程,所以上式可表示为
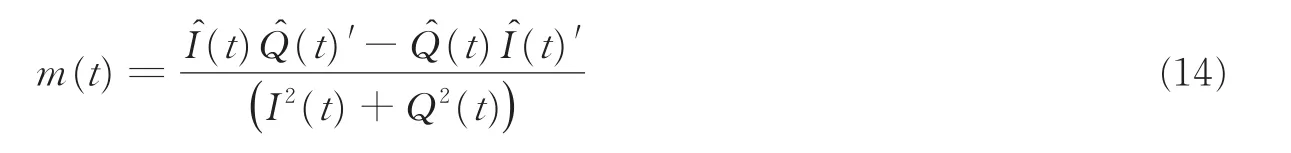
更多地,调频信号在基带是一个恒包络信号,即(I2(t)+Q2(t))=E,E为常数,式(14)可以表达为

式(15)中理想恒包络E=I2(t)+Q2(t)与实际正交适配基带信号包络Eˆ=Iˆ2(t)+Qˆ2(t)的区别在于,由于Eˆ引入了非理想正交变频带来的幅度和相位不一致性,使得其包络在恒包络基础上叠加了高频成分,可将Eˆ通过低通滤波器滤除高频成分得到E,即式(15)可表示为

对应数字域处理,则式(16)可表示为
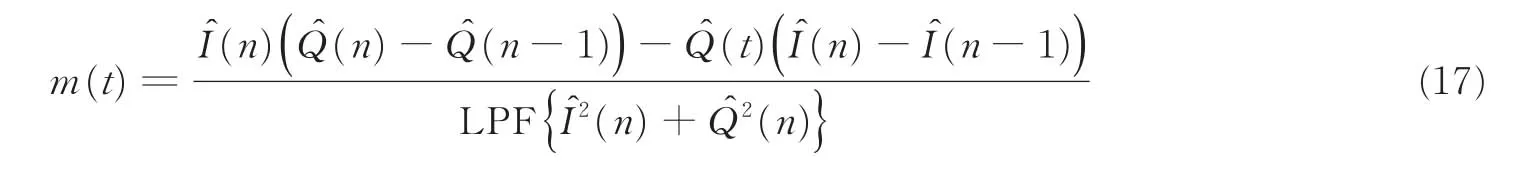
式(17)即是本文提出的抗正交失配特性鉴频算法,其中Iˆ(n)和Qˆ(n)是数字域基带失真信号,包含了射频域正交失配带来的幅度不一致和相位不正交特性带来的影响。式(17)算法虽然利用失真基带信号进行解调,但完全规避了正交失配带来的影响,使得解调后信号没有叠加任何由于正交失配带来的失真。实际工程应用中,若要考虑衰落信道,低通滤波的带宽应大于衰落信道引起的包络起伏的最大可能频率,目的是分母也保留信道衰落对包络影响,从而分子、分母相除抵消衰落信道包络起伏对解调的影响。
2 算法性能验证
2.1 仿真验证方法
计算机仿真验证框图如图2所示。仿真实验中被调信号为频率为500 Hz的单频信号,采样率120 kHz,信噪比为60 dB。
2.2 理想正交下变频仿真验证
设置如图2中正交下变频为理想正交下变频,即两路正交本振信号相位正交不一致性为0°,幅度大小不一致性为0 dB。图3、4即分别为反正切解调和本文提出的算法解调后的信号时域波形图。

图2 仿真验证Fig.2 Block diagram of simulation verification
由图3和图4可见,对于理想的正交下变频,无论反正切解调还是本文提出的算法解调波形都没有失真。具体地,由表1可见,两种方法解调性能一致。
2.3 非理想正交下变频仿真验证
设置如图2中正交下变频为非理想正交下变频,两路正交本振信号相位正交不一致性为5°,幅度大小不一致性为2 dB。图5、6即分别为反正切解调和本文提出的算法解调后的信号时域波形图。

表1 理想零中频结构下两种算法解调性能Tab.1 Demodulation performance of the two algorithms with ideal Zero-IF Structure
由图5和图6可见,对于相位正交不一致性为5°,幅度大小不一致性为2 dB的正交下变频情况下,反正切解调波形已经出现明显失真,而本文提出算法的解调波形仍然没有失真。具体地,由表2所示的SINAD指标可见,反正切解调性能在此种条件下已严重恶化,而本文提出的算法解调性能未受影响。

图3 理想零中频结构下反正切解调波形Fig.3 Demodulated signal wave of arc-tan discriminator with ideal Zero-IF Structure
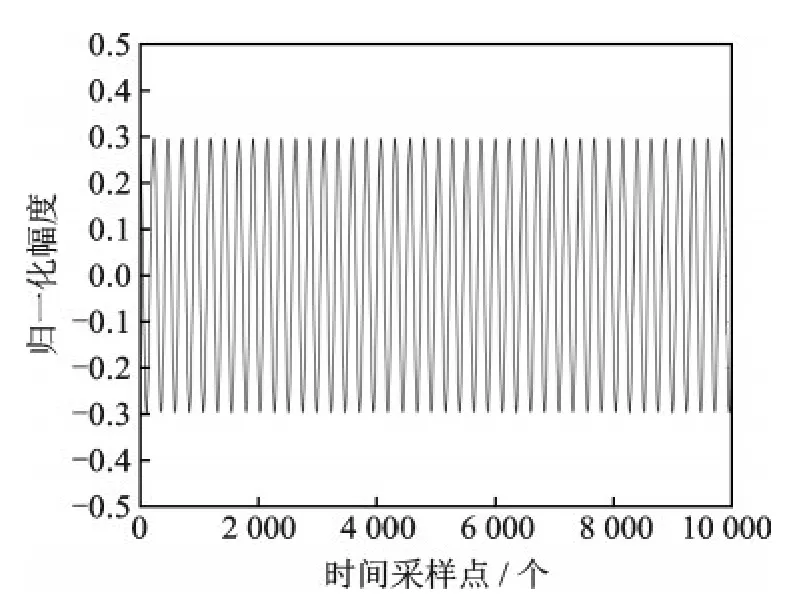
图4 理想零中频结构下本文提出的算法解调波形Fig.4 Demodulated signal wave of proposed algorithm with ideal Zero-IF Structure
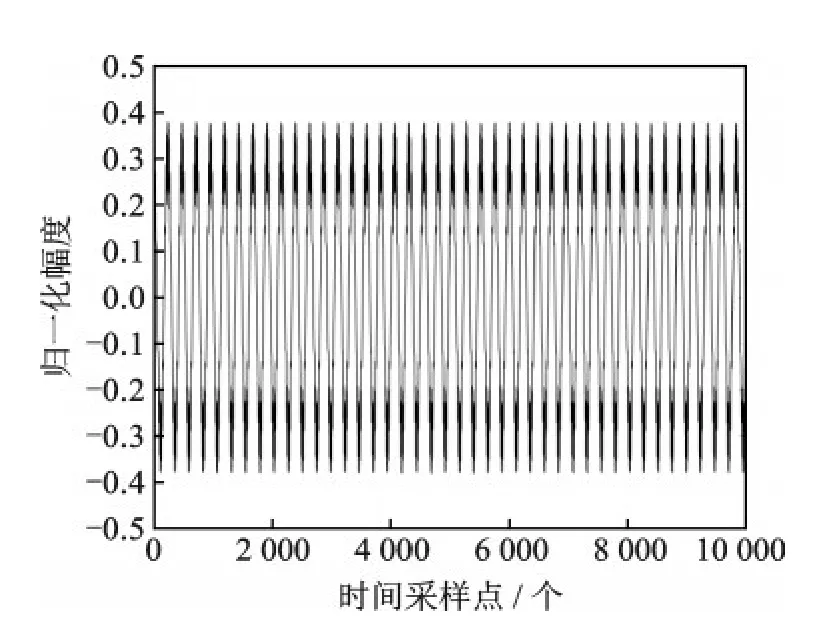
图5 实际零中频结构下反正切解调波形Fig.5 Demodulated signal wave of arc-tan discriminator with actual Zero-IF Structure

图6 实际零中频结构下本文提出的算法解调波形Fig.6 Demodulated signal wave of proposed algorithm with actual Zero-IF Structure
2.4 仿真验证解调性能
本小节,针对正交下变频不同的相位不一致性和幅度不一致性,对反正切解调算法和本文提出的抗正交失配算法进行横向全面的性能对比,结果见表3。从表3的仿真结果,可以得到以下结论:

表2 实际零中频结构下两种算法解调性能(5°,2 dB)Tab.2 Demodulation performance of the two algorithms with actual Zero-IF Structure(5°,2 dB)
(1)理想情况,即射频接收前端没有正交失配情况下,反正切解调算法和本文提出的抗正交失配算法的解调性能基本相同。
(2)随着射频前端正交失配特性的恶化,即两路正交本振的相位不一致性和幅度不一致性的加剧,反正切解调算法性能持续恶化。

表3 解调性能对比Tab.3 Comparison on demodulation performance
(3)随着射频前端正交失配特性的恶化,即两路正交本振的相位不一致性和幅度不一致性的加剧,本文提出的抗正交失配解调算法完全不受影响,性能良好,且与理想情况保持一致。
2.5 工程验证
在如图7所示的硬件平台验证了本文提出的算法的有效性及可靠性。由信号源产生调频信号,被调信号为500 Hz单音信号,调制最大频偏为5 kHz,载波频率为400 MHz。射频小信号板接收信号后正交下变频至基带,由于射频域正交下变频固有的正交失配特性,基带信号产生失真,之后经A/D采样后进入数字域处理,A/D采样率为120 kHz。在DSP内部分别进行反正切解调和本文所提出的抗正交失配解调算法解调出被调信号,送D/A输出到音频分析仪进行SINAD指标测试。由表4的测试结果可见,与反正切解调算法相比,本文提出的算法没有受到正交失配的影响,并且在重复性实验中,性能保持稳定。
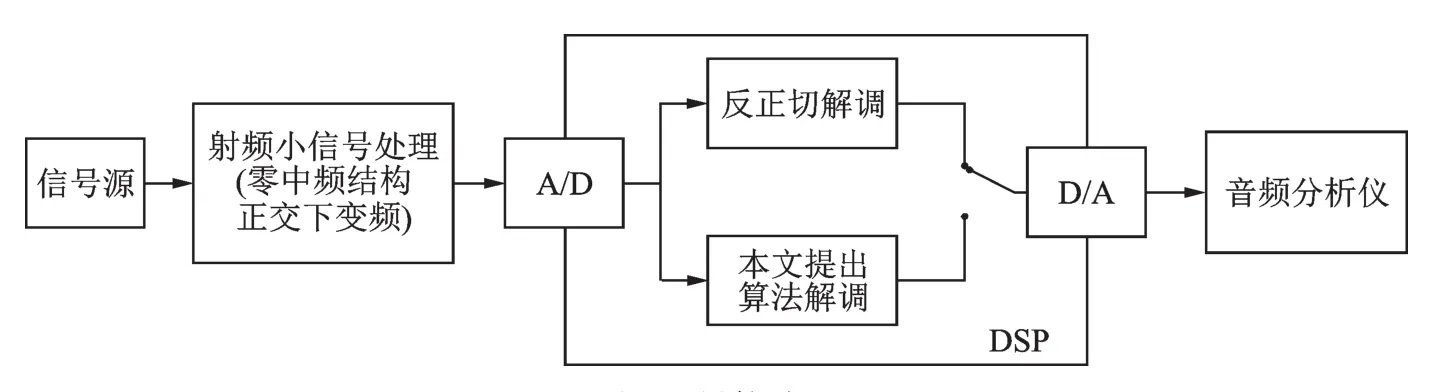
图7 硬件验证Fig.7 Block diagram of the hardware verification
2.6 算法适应性对比
在实际工程应用中,由于射频硬件固有的非理想特性,会影响包括调频体制在内的通信信号的传输,本节将针对功放非线性、本振泄漏、频偏3个典型的非理想特性对调频体制的补偿方法做出简要介绍,并给出本文提出的算法和传统反正切算法在适应性上的对比仿真结论。

表4 硬件验证解调性能Tab.4 Demodulation performance of the hardware verification
功放有着固有的非线性特性,在提高效率的前提下使功放工作在非线性区,不仅会造成带外失真即频谱的扩展,干扰临近信道,还会引入带内失真[9]。功放还具有记忆效应,即当前的输出不仅跟当前的输入有关,还跟其他时刻的输入有关。调频信号是典型的恒包络调制信号,在实际工程中,其峰均比极低,功放非线性不会造成调频信号的交叉调制从而引入带内、带外失真。调频信号也是典型的窄带信号,在实际工程中,其带宽一般在千赫兹量级,功放的记忆效应对调频体制几乎没有任何影响。
本振泄漏直接的影响是在对零中频基带接收信号中叠加直流成分,任何解调方法都会将直流误认为是有效信号进行解调,从而导致失真。在数字域可采用训练信号的自适应学习,解算出负相位的抵消信号。
由于发射机与接收机时钟源的相对独立以及晶振固有的频率偏差,频偏始终存在于通信信息系统。对于调频信号来讲,直接导致解调后的信号叠加一直流成分,利用此直流与频偏的正比例对应关系,逆向调节接收本振频率,最终使得直流成分消失,即频偏纠正完毕。
如图8所示即为调频信号考虑正交适配在内的4种非理想特性的算法仿真验证方案。其中功放采用记忆多项式模型阶数为5,记忆深度为2,本振泄漏大小为-40 dBc,频偏为400 Hz。仿真结果见表5。

图8 对比验证框图Fig.8 Block diagram of comparison verification

表5 多非理想条件下解调性能对比Tab.5 Comparison on demodulation performance with multi non-ideal conditions
通过表5与表3的性能对比,可以看出本文提出的解调算法与反正切算法在功放非线性及本振泄漏、频偏条件下的适应性能力一致,且解调性能如2.3节所述完全优于反正切解调。
3 结束语
本文针对零中频接收机结构中两路正交本振固有的相位不完全正交性和幅度不完全一致性,利用FM信号自身特点,提出了一种抗正交失配特性的FM解调算法。此算法不需要额外的训练、数学建模和模型参数解算等复杂过程,也不需要额外的硬件开销,简单易行。仿真及工程验证结果表明,本文所提出的算法具备天然的抗正交失配特性,具备完全跟踪特性。在各种正交失配情况下,都与理想正交下变频时具备良好且一致的解调性能,且对于实际通信硬件系统的典型非理想特性即非线性、本振泄漏、频偏,本文所提出的算法与传统反正切算法具有相同的适应能力。
