基于跳周期变换的多跳信号特征盲提取方法
2019-10-30卓欣然郭海召窦修全
卓欣然,郭海召,窦修全
(1.电子科技大学,四川 成都 611731;2.中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
跳频通信独特的低截获概率、强抗干扰能力、高保密性等优点对跳频通信链路天基侦察提出了极其严峻的考验[1-2]。尤其针对多跳频信号的参数盲估计,仍然是当前军事通信领域研究的热点与难点。通常跳频信号的跳周期、跳时和频率集等是跳频通信侦察系统重点估计的特征参数,目前针对参数估计、自相关技术、时频变换以及小波、图像处理等方法是目前主要采用的算法。
例如Chung C D,Polydoros A通过采取多跳自相关技术实现了跳速的估计[3-4],但该理论需要预先知晓跳频信号精确功率与大致跳速取值范围。文献[5]在文献[4]的基础上,提出了一种迭代方法适用于同时估计跳周期和信号幅值信息。该算法虽然不需对信号功率预先知晓,但是计算负担大大提高了。时频变换是分析跳频等非平稳信号的有效工具,文献[6-7]中给出了较为详尽的分析,例如短时傅立叶变换(Short-Time Fourier Transform,STFT)时域精度与频域精度存在矛盾,威格纳分布(Wigner-Vile Distribution,WVD)和伪威格纳分布(Pseudo Wigner-Vile Distribution,PWVD)虽然时频聚焦性能良好,但代价是不仅计算量较大,而且存在较为严重的交叉项干扰,平滑伪威格纳分布(Smooth Pseudo Wigner-Vile Distribution,SPWVD)则以相对更大的计算负担消除了多个信号的交叉项干扰。文献[8]则利用STFT作为跳频信号时频域映射的分析工具,在此基础上,为了提高跳周期的估计精度,采用了小波变换与时频谱分析方法。文献[9]在原始STFT的基础上提出了滑变窗长自适应选择的方法,一定程度上缓解了STFT的固有缺点,但同时引入了更大的计算负担。
文献[10]将截获到的跳频电台信号作谱图映射变换,采用图像处理领域中的经典算法对变换结果作初步优化,在提取谱图图样的时频脊线之后,利用多次差分的方法即可在峰值处提取跳变时刻,结合所有的跳频信息进一步完成后续跳速、频率等参数测量。该算法步骤流程较为复杂,且受信噪比影响较大。文献[11]将时频映射的方法与小波变换相结合,按照跳周期、跳时、跳频频率的估计顺序,在SNR>0 dB时,取得了接近克拉美-罗下界(Cramer-rao Lower Bound,CRLB)的效果,但是当SNR<0 dB时,估计性能迅速下降。
现有的参数估计方法多是针对单跳频信号,多跳频信号的参数估计问题研究相对较少。文献[12]通过盲源分离的方法实现了对宽带跳频信号的参数估计,但该方法只适用于正交组网信号;文献[13]基于空间极化时频分布在欠定条件下完成多跳频宽带信号的DOA和极化状态联合估计,能够适应不同的组网信息,但须提前预知信号的频率集,且运算量较大
基于上述问题,在谱图变换与非相干积累的基础上,提出一种基于跳周期变换的方法提取多跳频信号特征参数。首先采用二维恒虚警检测与矩形窗搜索算法实现二维峰值位置的准确提取,将其时间维信息多次进行跳周期变换,通过计算自适应门限检测变换域谱线峰值,并采用序列检索的方式实现跳周期、跳时、跳频频率集等的参数估计。该方法实现了多跳信号的特征参数盲估计,在恶劣噪声环境及丢跳情形下取得优良实践效果。
1 跳频信号建模
假设接收设备的带宽足够宽,跳频信号所有载频都可以截获的条件下,那么在0~t的观测时长,接收到的跳频信号共有K跳,每跳对应频率fi,i=1,2,...,K,跳周期用TH表示,第一跳作为跳时,用Tinit表示,最后一跳持续时间用TK表示,则跳频信号的时频信息如图1所示。

图1 跳频信号时频特征图
跳频信号可以看作多个定频信号移位累加的MFSK调制[14-15],同时要求定频信号的载频按某种规则依次变化,由此可知跳频信号s(t)的数学表达式为:
(1)
(2)
式中,a(t)为信号复包络,φ(t)代表跳频信号相位变化,φi,i=1,2,...,K是其初相。当多个跳频信号均出现在有限的侦察时长内,则进一步得到:
(3)
2 多跳信号特征提取理论
2.1 二维峰值提取
由于谱图变换不会引入新的交叉项且具备优良的聚焦性能[16-17],选用谱图变换与非相干积累作为时频映射工具。当环境信噪比SNR=0 dB时,采用恒虚警检测技术[18]得到二维峰值检测结果如图2所示。直接提取二维峰值得到的峰值较多且混乱,跳频信息混叠严重,可以看到,噪声环境较为恶劣,并不能在每一时刻均能提取到峰值,而是呈现“断码”的情况,甚至会出现完全丢失某一跳的信息。解决这一问题的办法就是对提取得到的二维峰值进行修正,即采用矩形搜索窗搜索整个时频平面。矩形窗的宽度常常取一个频域分辨率,考虑噪声的影响,仿真实验中取2。
在搜索到峰值的矩形搜索窗内,对所有峰值位置取均值,得到二维峰值新的位置。即:
(4)
处理之后的时频峰值如图3所示,最终得到了较为干净的二维峰值矩阵,在每一载频的驻留时间段内只保留了一个时频点,并将这个时频点对应的横坐标称之为中心时刻,用hcti,i=1,2,...,N表示,其中N为跳频频率总个数。

图2 二维时频峰值检测
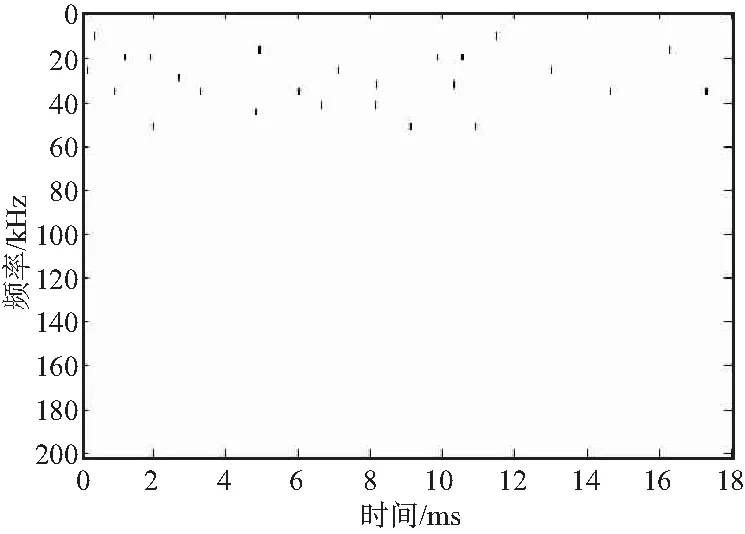
图3 修正后的时频检测峰值
2.2 跳周期变换算法
2.2.1 算法原理
基于二维峰值的时间维信息,跳周期估计的思路则是对交错的多跳频信号的中心时刻进行跳周期变换,形成跳周期谱线,然后设置自适应门限,提取超过门限的谱峰对应的时刻即可作为多个跳周期的估计值。
设定提取到的多跳频信号中心时刻用tn,n=1,2,...,N表示,N为提取到的跳频信号中心时刻数量,用公式可表示为:
(5)
则基于跳频中心时刻变换的跳周期估计方法可由下式给出:

(6)
式中,g(t)为提取到的中心时刻;D(τ)为跳周期变换谱线。通常会由于丢跳等原因使得D(τ)在跳周期的整倍数位置出现峰值,将这种出现的波峰称为子谐波,跳周期变换法通过引入相位因子exp(j2πt/τ),j=sqrt(-1)来达到抑制子谐波的目的。
为了便于分析,采用跳周期变换的离散形式。假设[τmin,τmax]是要分析的跳周期范围,将这个范围划分成K个小区间,这K个区间的宽度相等,区间的宽度为b=(τmax-τmin)/K,则第k个区间的中心为:τk=(k-1/2)b+τmin,k=1,2,...,K。跳周期变换法的离散形式可表示为:
(7)
若b→0,则Dk/b→D(τ),可用|Dk|来表示跳周期的谱线。通过变换,在真实的跳周期上会出现峰值,通过峰值位置即可确定跳周期的估计值。
在提取到的跳频中心时刻没有抖动的情况下,传统的跳周期变换法对子谐波的抑制有着不错的效果。但实际情况中,往往由于噪声等影响,跳频中心时刻通常存在一定的抖动甚至丢跳现象发生,那么随着中心时刻远离时间起点,跳周期变换的相位因子的相位误差就会增大。同时由于抖动,本应该在同一个区间的跳频驻留时间分布在相邻的几个区间内。为解决上述问题,这里通过使用可变的时间起点以及交叠的区间划分对跳周期变换法进行修正[19-20]。
(1) 可变的时间起点
在没有丢跳的情况下,跳频中心时刻对(tm,tn)中的tm和原始起始时间相同。但是实际条件下抖动及丢跳现象经常存在,为了减小相位误差,下面设定了需要改变时间起点的条件。
首先计算初始相位η0=(tn-Ok)/τk,Ok为第k个区间的原始时间起点,用τk来代替tn-tm以减小中心时刻抖动的影响。进一步分解相位η0=υ(1+ζ),υ为整数,ζ为一实数,且有-1/2<ζ<1/2。那么依据下面条件判断是否需要转换时间起点:
当υ=0时,时间起点不变;
当υ=1时,如果tm=Ok,则用tn作为新的时间起点;
当υ≥2时,如果|ζ|≤ζ0,则用tn作为新的时间起点。
经过上述步骤,时间起点的改变并不会积累相位因子误差,较大地减弱了相位因子积累误差带来的影响。
(2) 交叠的跳周期区间
为了避免因跳频中心时刻抖动造成跳周期谱峰值减小,这里采用交叠的跳周期区间。假设ε是中心时刻抖动的上限,K是划分的跳周期区间个数,则每个跳周期区间的宽度改变为bk=2ετk,若bk 其实中台化背后的核心理念还是平台化和生态化。它跟整个互联网20年来发展的脉络基本是一致的。当阿里在用平台化、生态化的方法推动整个电子商务生态健康发展时,最核心的是提供了各种各样的基础服务。但是要真正对外提供平台化的服务,企业就会发现面临一个重大挑战:内部的所有技术怎么变成服务? 2.2.2 门限设定 为了检测到真实跳周期,这里根据观察时间原则,消除子谐波原则以及消除噪声的原则来设定检测跳周期的门限,具体推导见文献[20]。设置门限如下,即: (8) 式中,α,β,γ可调,可根据实际情况加以调整,通常取γ≥3;T为整个观测时间;ρ为跳频中心时刻密度。 设有2个跳频电台,跳周期分别为TH1=1.0 ms,TH2=1.6 ms,设定检测到的跳频中心时刻抖动百分比为1%,采用本文提到的跳周期变换法得到的谱线以及门限检测效果如图4所示。 图4 跳周期变换法检测效果 过门限的谱线峰值位置即可作为估计得到的跳周期的值,图4中,2组峰值位置分别在1,1.6 ms附近,取均值分别为1.01,1.62 ms。初步论证,本文所提方法能够较为准确地检测到正确跳周期的位置。 2.2.3 算法流程 图5 跳周期变换法完整流程 综上所述,多跳频信号参数盲估计可以分为时频映射、二维峰值提取以及特征参数生成3个部分。本小节给出多跳频信号特征参数的提取流程,如图6所示。 图6 多跳信号特征参数提取流程 跳周期估计的过程中伴随着对应跳频中心时刻的序列检索,即将属于不同电台信号的中心时刻序列与对应的跳周期参数均保存在缓存空间,再以此为数据输入,进一步估计得到跳时等特征参数。 本小节将对本文算法在不同信噪比下的性能进行分析,表1列出了仿真实验所需条件。 表1 多跳频信号参数估计仿真条件 项目描述信号时长/msT=24采样率/kHZfs=200窗长L=64平滑因子ΔM=8跳周期/msTH1=1.0,TH2=1.6跳时/msTinit1=0.6,Tinit2=1.0跳频频率在0~0.5(归一化频率)中取值,相邻频率间隔大于频域分辨率(fs/L) 在每个信噪比下均作100次Monte-Carlo仿真,得到跳周期、跳时以及跳频频率的估计性能曲线图分别如图7、图8和图9所示。 图7 多跳信号跳周期估计方差 随着噪声环境的改善,跳周期估计方差在逐渐改善,同时,由于基于跳频中心时刻变换的跳周期估计算法对丢跳发生时较强的适应能力,使得信噪比在-4 dB时,跳周期参数的估计方差仍然在10-8量级。 图8 多跳信号跳时估计方差 图9 载频归一化估计方差 跳时与跳周期的估计方差曲线类似,跳频频率由于在频率轴取值,相对于跳周期及跳时估计,受信噪比影响较小。 考虑跳频信号跳丢失的情况,进一步检验所提算法的鲁棒性能。采用表1的仿真参数,设定丢跳率从5%~25%变化,选择跳频中心时刻抖动误差百分比为1%。这里将本文算法与文献[21]中的逐次差分直方图法进行比较。图10展示了2种算法的对比效果,图中虚线表示无丢跳时的跳周期估计方差。 (a)跳频电台一 (b)跳频电台二图10 不同丢跳率下跳周期估计性能对比 将跳频信号无丢失数据时估计得到的跳周期估计方差作为基准,本文所提的算法基本可以看出是围绕基准线的波动,而差分直方图法却是随着丢跳数的增加,估计性能逐渐变差。可以得到,本文所提算法的鲁棒性能更加优越。 本文将基于跳周期变换的方法应用于跳频信号特征参数的提取过程,采用序列检索与多次跳周期变换实现多跳频信号参数集的准确提取。主研算法在适应恶劣噪声环境和丢跳方面表现优良,在多跳频信号盲估计领域内提供了较为新颖的思路,为跳频通信链路侦察的工程实用化及天基装备系统的完善提供了较为有效地理论支撑。

2.3 处理流程
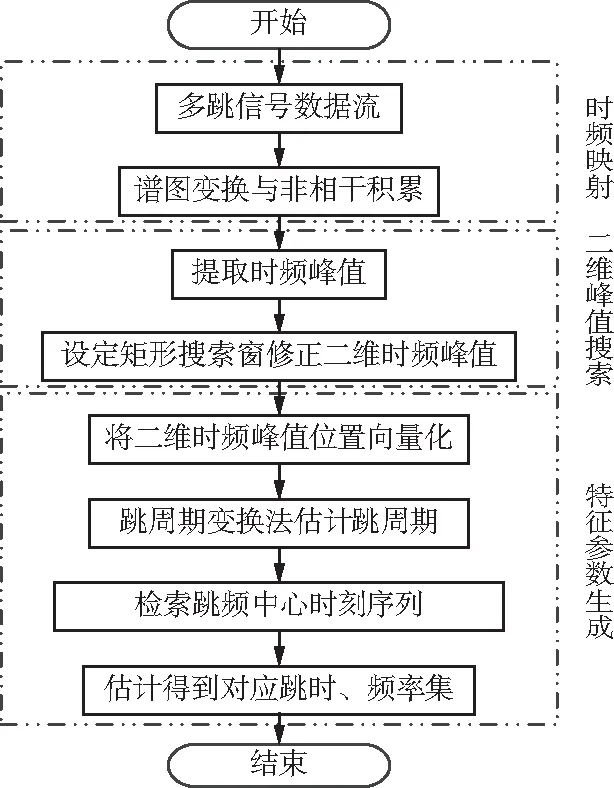
3 性能分析
3.1 估计性能验证



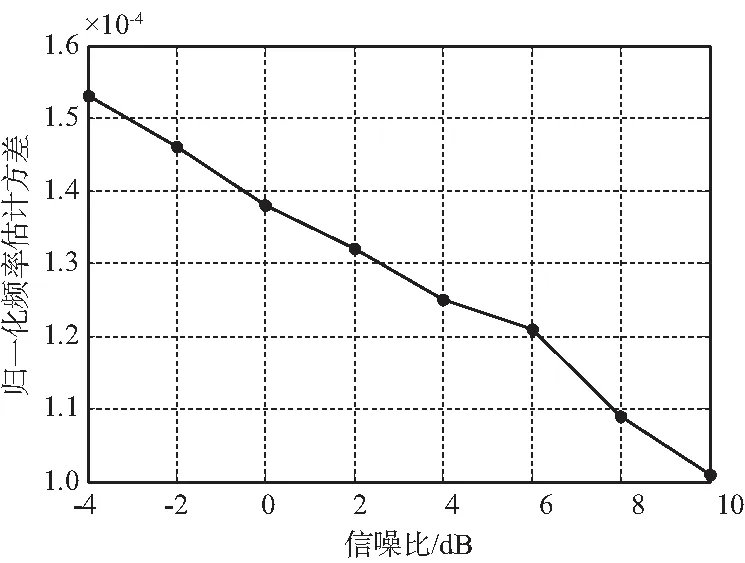
3.2 丢跳适应性能验证


4 结束语
