基于AdaGrad的GNSS-R镜面反射点自适应预测算法
2019-10-30盛志超杜璞玉
盛志超,周 勃,杜璞玉,秦 瑾,王 路
(1.上海航天电子技术研究所,上海 201109;2.东南大学,江苏 南京 211189)
0 引言
GNSS-R技术是一种新型遥感技术,能够实现对海面高度、海面风速和土壤湿度等多种环境要素的探测[1-2]。相比于传统微波遥感载荷,GNSS-R载荷具有宽刈幅、高时空分辨率、低功耗和低成本等优点[3-5]。
GNSS-R遥感的探测区域是以镜面反射点为中心的闪耀区——反射信号功率最集中的位置[6-7]。对镜面反射点几何位置的精确预测有2个作用:① 建立对GNSS-R遥感探测的坐标基准;② 实现对反射信号的实时开环跟踪。镜面反射点预测的精确与否,对GNSS-R遥感探测的建模与反演有直接影响。因此,如何快速有效地计算出镜面反射点的位置,是GNSS-R技术的首要问题。
现有的镜面反射点预测算法主要有Gleason算法[8]、S.C.Wu算法[9]和线段二分法[10]。Gleason算法的精度高但收敛速度慢;S.C.Wu算法的收敛速度快且稳定,但因其采用地球圆模型进行建模,需要加入复杂的校正;线段二分法是S.C.Wu算法的改进,其收敛速度快并且精度高,但存在不可避免的径向和法向不统一问题。
镜面反射点的预测过程本质上和深度学习中的“学习”过程是一致的,因此,一些统计学习理论可以用于镜面反射点预测的优化。本文提出了一种基于AdaGrad优化的GNSS-R镜面反射点自适应预测算法,能够对学习效率进行自动调整,从而实现对镜面反射点更高效、更精确的搜索。
1 镜面反射点
GNSS-R几何位置关系示意图如1所示。图1(a)中GNSS卫星发射GNSS信号,该信号到达地球表面时,在镜面反射点所在的闪耀区发生散射和反射,反射信号由GNSS-R接收机接收[11-12]。在理想情况下,镜面反射点满足以下条件:① 镜面反射点在地球表面;② 发射机—镜面反射点—接收机是所有反射路径中的最短路径;③ 满足斯涅耳定律——入射角等于反射角[13]。
图1(b)中,R表示接收机,T表示发射机,S表示地球表面上的某点,O表示地心,M表示OC所在直线与RT所在直线的交点,U表示R关于OM的对称点,C表示M关于RU的对称点,αt,αr分别表示信号的入射角和反射角。
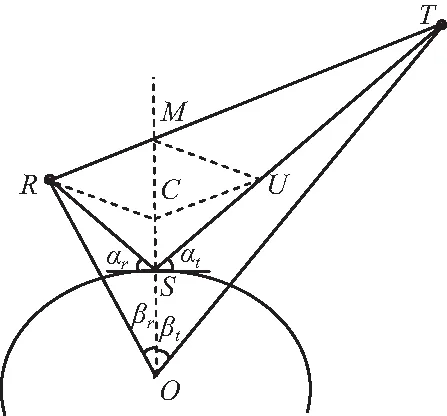
(b)二维视图
在理想条件下,利用镜面反射点满足的3个条件,对镜面反射点的预测问题等价于非线性约束条件下的非线性优化问题,其数学模型可以表示为:
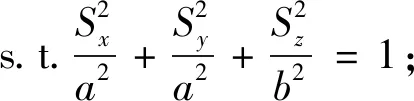
(1)
式中,f(S)的最小化函数是镜面反射点预测的目标函数;R表示接收机;T表示发射机;S表示地球表面上的某点;Sx,Sy,Sz分别为S在地心坐标系下对应的三轴坐标;αt,αr分别表示信号的入射角和反射角。
2 镜面反射点的估算
传统镜面反射点预测算法都是以入射角等于反射角为终止条件进行搜索的,得到的反射路径长度不一定最短,不符合镜面反射点的定义。本文提出的算法将直接从式(1)中的目标函数出发,在地球表面寻找使反射路径长度最短的点,即镜面反射点。下面会证明本文提出的算法所预测得到的镜面反射点同时也满足入射角等于反射角这一条件。
针对带非线性约束条件的非线性优化问题,镜面反射点初始值的设置会对算法的收敛速度以及结果的准确度产生重要影响。因此,本文提出的算法将通过以下2个步骤实现对镜面反射点的预测:
① 利用发射机、地球、接收机的几何关系,实现镜面反射点的粗略估计;
② 利用AdaGrad优化算法求解最短路径,实现镜面反射点的精确估计。
2.1 镜面反射点粗估
图1(b)中存在如下数学关系:
|RM|=|MU|=|UC|
|RM|/|RT|=|RM|/(|RM|+|MT|)=
|CU|/(|CU|+|MT|)=
|SR|/(|SR|+|ST|)≈
|OR|/(|OR|+|OT|)。
(2)
由此可以得到,M的粗略估计值为:
M=R+RM≈R+[|OR|/(|OR|+|OT|)]×RT。
(3)
而镜面反射点S1为M的星下点,则镜面反射点的粗略估计值为:
S1=(OM/|OM|)×Re,
(4)
式中,Re为WGS-84坐标下M点对应星下点的半径。
2.2 镜面反射点精估
2.2.1 AdaGrad优化算法
深度学习使用数据对其构筑中的参数进行更新以达成训练目的,该过程被称为“学习”,“学习”的常见方法有梯度下降法及其变体,一些统计学习上的理论被应用在学习过程的优化上[14]。
针对反射路径长度f(S)=|S-T|+|R-S|的最小化问题求解,同样也可以通过梯度下降的方法实现对解的优化更新,其更新表达式为Sn+1=Sn-K·f(Sn)[15]。其中,K表示学习率,f(Sn)表示f(S)的梯度,即每一次迭代过程中的更新增量,其可以表示为:
(5)
梯度下降法在每一次迭代过程中,对解的更新都采用固定的学习率。学习率决定了参数移动到最优值的速度快慢。如果学习率太小,优化效率可能过低,算法收敛速度太慢;如果学习率太大,参数的收敛过程会产生震荡,甚至无法收敛[16]。
本文采用深度学习中的AdaGrad优化算法。该算法是梯度下降法的一种变体,能够在每一次迭代过程中对学习率进行调整,当离目标函数最优解较远时,学习率较大,朝最优解移动得越多[17]。随着迭代次数的增加,学习率逐渐减小。
基于AdaGrad计算镜面反射点的算法具体如下:
① 对参数进行初始化:
设置全局学习率ε为1,镜面反射点的初值为上节镜面反射点的粗估值S1,常数δ为10-7,梯度累积变量τ为0。
f(Sn)n=N(Sn)×f(Sn)×N(Sn),
(6)
式中,N(S)表示S的单位法向量。
监管点设立后珠海局多措并举,严密监控监管点周边水域的渡口,渡船以及桥梁的安全,发扬“敬业、工匠、团队”的精神,每天安排执法人员前往“海趸1556”值守,重点开展电子巡航和对赤粉水道、荷麻溪水道、泥湾门水道、虎跳门水道、磨刀门水道进行巡航检查:“海趸1556”监管点设立以来,共检查船舶1716艘次,检查渡口541次,桥梁水域巡查1141次,开展夜巡56次。随着“海趸1556”监管点的投入使用,珠海局依托该监管点进一步提高了现场监管效率,加大了违章、违法行为的打击力度,强化了辖区渡口、桥梁、岔河口等重点水域的监管力度,周边水域通航秩序大有改观,未发生重大事故,极大地助力了“平安西江”建设。
③ 计算累积梯度平方和τ:
τ=τ+f(Sn)2。
(7)
④ 计算更新增量ΔS:
(8)
⑤ 利用ΔS,对Sn进行更新:
S′=Sn+ΔS。
(9)
⑥ 将S′映射到地球表面,得到相应的镜面反射点的下一个解Sn+1:
Sn+1=(OS′/|OS′|)×Re(S′)。
(10)
⑦ 计算更新幅度:
COR=|Sn+1-Sn|。
(11)
如果更新幅度COR大于设定的阈值则继续进行下一次迭代,否则结束迭代,输出镜面反射点的最优解。
2.2.2 预处理
预处理实现将WGS椭球面通过坐标变换映射成单位圆[18]。其坐标变换的矩阵F为:
(12)
式中,a=6 378 137 m是赤道半径长度;b=6 356 800 m为经线半径长度。
坐标系映射的示意如图2所示,其中,R表示接收机,T表示发射机,SWGS-84表示WGS-84椭球面上的镜面发射点,q表示f(S)在点SWGS-84处的梯度,n表示点SWGS-84处的法向量,Spro表示单位圆上的镜面反射点,q′表示f(S)在点Spro处的梯度,n′表示点Spro处的法向量。
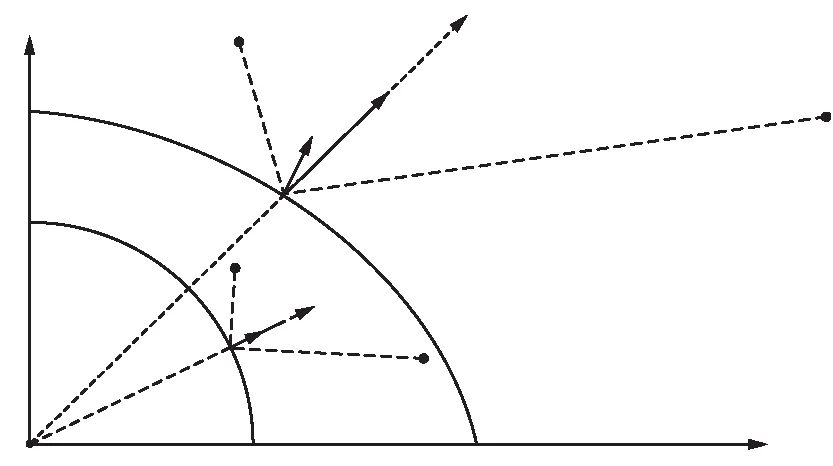
图2 坐标映射示意
将WGS-84椭球面通过坐标变换映射成单位圆,具有以下2个作用:
① 实现了地球尺度和收敛因子数量级的统一。通过坐标变换,将赤道半径a=6 378 137 m,经线半径b=6 356 800 m的WGS84椭球面映射成单位圆,使地球尺度和收敛因子在同一数量级上,以便在镜面反射点的最优解求解过程中能够快速获得有效解。
② 实现镜面反射点的径向和法向的统一。如图2所示,点SWGS-84处的目标函数下降最快的方向为f(Sn)的方向,即图中径向q。因此,算法只有在径向q的水平分量为0时收敛。但是径向q的水平分量只有在R,O,T共线且该直线与地平线垂直的时候才为0,即入射角为90°时。而在单位圆中,径向q与法向n共线,当算法收敛时,即修正幅度COR为0时,径向q的水平方向分量为0,又因为q=(Sn-T)/|T-Sn|+(Sn-R)/|R-Sn|,可知径向q是2条单位向量的矢量和,只有入射角等于反射角时,径向q无水平分量。
2.2.3 算法流程
上面提出的基于AdaGrad计算镜面反射点算法的基础上,增加了预处理操作,因此本文总的算法流程如图3所示。

图3 算法流程
3 仿真分析
利用STK和Matlab进行联合仿真实验。GNSS卫星采用GPS卫星,轨高20 200 km,LEO卫星轨高700 km,进行了4种算法反射路径长度和运算效率比较仿真以及本文算法迭代次数稳定性仿真。发射机T的坐标为(-11 178 791.991 29,-13 160 191.204 99,20 341 528.127 54),接收机R的坐标为(-4 069 896.491 51,-3 583 236.963 73,4 527 639.271 75)。
3.1 4种算法反射路径长度和运算效率比较仿真
4种算法反射路径长度和运算效率仿真图如图4所示。
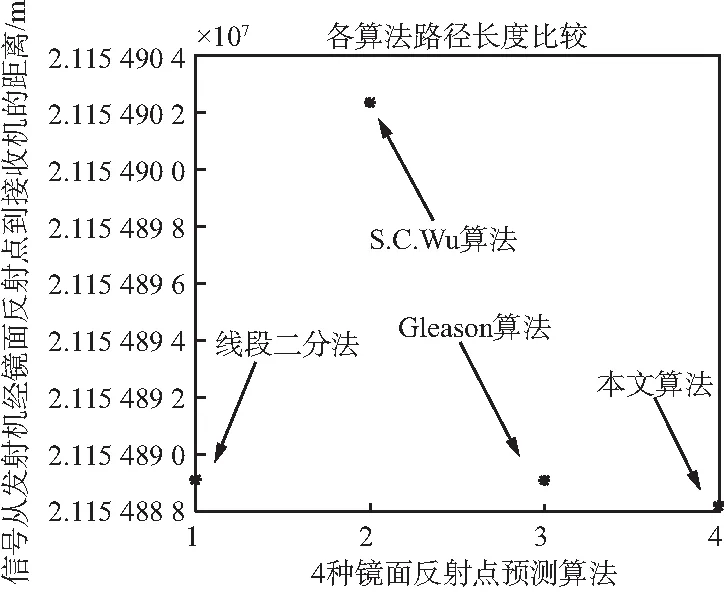
(a)反射路径长度
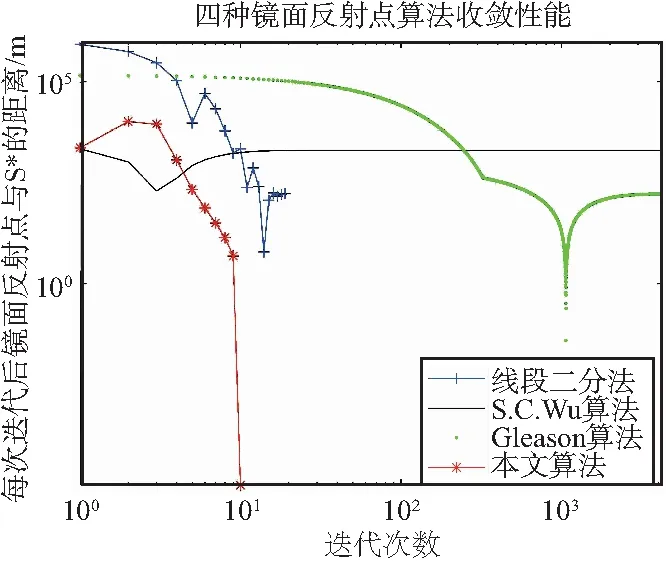
(b)收敛性能比较图4 种算法反射路径长度和运算效率仿真
从图4可以看出,S.C.Wu算法得到的反射路径最长,其获得的镜面反射点与真实镜面反射点距离最远,因此,该算法计算精度最差。其他3种算法的路径长度接近,其中本文算法的路径长度最短,满足最短反射路径的特点。4种算法预测得到的镜面反射点在地图上位置相近,说明本文算法得到的镜面反射点是有效的。
将仿真中本文算法计算得到的镜面反射点S*作为参考,对算法的收敛性能进行分析。图4(a)为4种镜面反射点算法收敛性能的比较结果图。从图4(b)可以看出,S.C.Wu算法无法收敛,Gleason算法迭代次数多,运算速度较慢。本文算法迭代次数最少,速度最快。
3.2 本文算法高效性统计意义仿真
利用STK生成的1颗轨高700 km的LEO卫星和31颗GPS卫星进行仿真,仿真时间是从2015年3月7日00:00:00开始的24 h。GNSS-R接收机的下视天线的波瓣宽度为±45°,采用的选星策略是GNSS-R接收机的仰角不低于75°。
分别利用本文算法和线段二分法计算32 750组符合条件的数据。本文算法和线段二分法效率统计图如图5所示。通过比较可以看出,本文算法每次的迭代次数稳定在14次以内,线段二分法每次的迭代次数集中在13~17次,部分数据的迭代次数超过25次,因此本文算法从统计意义上来说运算效率明显优于线段二分法。
3.3 结论
Gleason算法收敛速度慢,但是位置较为精确;而S.C.Wu算法因其精度低、无法达到预设的精度要求,出现了无限次迭代,算法无法终止;线段二分法是S.C.Wu算法的改进,因此它继承了S.C.Wu速度快的优点,并且利用WGS-84椭球面,其预测得到的镜面反射点较为精确,但没有解决径向、法向不统一的问题。本文提出的算法能够根据更新幅度自适应的改善学习率,因而能更快速地到达最优解。通过仿真结果可以看出,本文算法的结果相比于其他算法更为精确。此外,根据图5结果可以得出,本文算法统计意义上也更加高效。
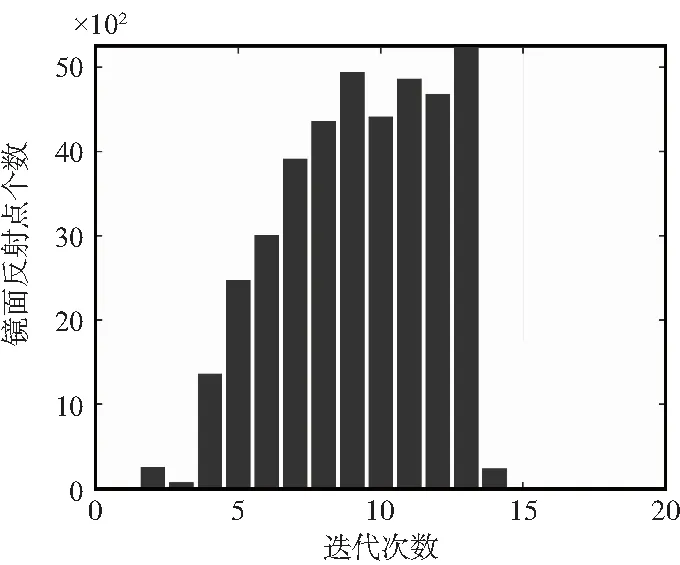
(a)本文算法效率统计图
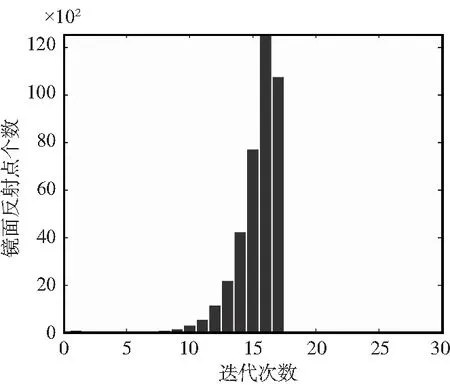
(b)线段二分法效率统计图图5 本文算法和线段二分法算法效率统计仿真
4 结束语
本文提出了基于AdaGrad的GNSS-R镜面反射点预测算法,具有精度高、速度快的优点。该算法将深度学习优化算法应用于镜面反射点的预测过程,通过自适应地调整学习率,提高算法收敛速度,满足星载环境中的实时性需求。该算法在预处理过程中实现镜面反射点径向和法向的统一,进一步提高了算法的预测速度。仿真结果表明,该算法收敛速度快,预测精度高。相比于传统镜面反射点预测算法,该算法在预测速度方面具有明显优势,对于GNSS-R载荷搭载具有一定的参考意义。
