LF-PSO优化神经网络的高压断路器机械故障诊断

(西安工程大学 电子信息学院，陕西 西安 710600)

高压断路器在电力系统起着非常重要的作用，为了提高电力系统运行的安全性和可靠性，对它进行故障诊断是十分有必要的，这样可以在还没发生故障或者快要发生故障时诊断出故障类型及时处理，避免大范围停电[1]。高压断路器中的机械故障占其总故障的很大一部分，而它的分合闸电流数据易获得，可以通过该数据集训练得到特征量与故障分类结果之间的关系，从而诊断出不同的故障类型[2-3]。

现如今有很多学者研究诊断高压断路器机械故障的方法，其中神经网络得到广泛应用。文献[4]使用PNN神经网络；文献[5]使用粒子群改进的最小二乘支持向量机方法；文献[6]使用粒子群优化的BP神经网络实现对其的诊断；文献[7]使用粒子群优化RBF神经网络方法；文献[8]证明了基于莱维飞行优化的粒子群算法比基本粒子群算法、布谷鸟算法以及蜂群算法具有更优的解和更快的收敛速度，本文将该算法用于对PNN神经网络参数平滑因子的寻优中，从而实现对其的诊断。

1 LF-PSO算法

1.1 粒子群优化算法

PSO算法是一种进化算法，来自于对鸟群捕食行为的研究，它从随机解出发，通过迭代寻找最优解，通过适应度来评价解的好坏[9]。每个寻优的问题解都被看成一个粒子，所有粒子在一个D维空间中进行搜索。在D维空间中有m个粒子x=(x1,x2,…,xm)，每个粒子i都有自己的位置和速度，分别表示为xi=(xi1,xi2,…,xiD)和vi=(vi1,vi2,…,viD)。第i个粒子目前搜索到的最优位置和整个种群目前搜索到的最优位置分别表示为pi=(pi1,pi2,…,piD)和pg=(pg1,pg2,…,pgD)。在每一次迭代中，粒子通过跟踪这两个极值来更新自己的位置和速度，粒子i的第D维速度更新公式为

(1)

粒子i的第D维位置更新公式为

(2)

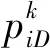
不同粒子的惯性权重ω不仅受到迭代次数的影响还受到距离全局最优点距离的影响，采用非线性动态惯性系数公式对其进行调整[10]，公式为

(3)

式中，fit为粒子实时的适应度值；fitavg为当前所有粒子的平均值；fitmin为当前所有粒子的最小值。

1.2 莱维飞行

莱维飞行(Levy Flight,LF)是一种短距离的搜索与偶尔较长距离的行走相间的行走方式，它不仅能增加种群多样性，还能扩大搜索范围，所以经它优化的算法更易跳出局部最优点[11-12]。

LF的位置更新式为

(4)

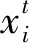
1.3 基于LF的粒子群优化算法

粒子群算法前期收敛速度快，但进化后期收敛速度慢且收敛精度低。通过研究发现，LF 能有效地使粒子通过随机游走产生新的解，经历新的搜索路径和领域，从而增加了种群的多样性，提高发现更优解的概率，不易陷入局部极值[13]。

LF对粒子的调整是通过改变粒子位置来更新粒子状态。在粒子群更新公式中速度项v保留了上代粒子的移动方向，使得粒子位置的更新方向受到上代粒子位置的影响较大而丧失多样性，从而易于陷入局部最优。同时这也与LF的随机游走理念相违背。为避免 PSO 算法更新公式中速度项v对LF调整粒子位置的影响，本文采用如下公式对粒子群更新公式进行改进。

(5)

虽然LF能够使解摆脱局部收敛，重新搜索解的空间，但无法保证其寻找到的新解一定优于原来的解。为了解决这个问题，使用贪婪的更新评价方法，该方法能够进行局部搜索来获得更优的解。令

(6)

(7)

因此LF-PSO算法将式(1)、式(2)改进为

(8)

式中，fit(x)为适应度函数。

2 LF-PSO算法优化PNN神经网络的故障诊断模型

2.1 PNN神经网络

PNN神经网络是一种能够用来进行分类的神经网络，其实际上是基于Bayes分类规则与Parzen窗的概率密度函数估计方法发展而来的并行算法[14]。PNN神经网络的结构如图1所示，它共有4层，具体层类别和神经元个数如表1所示。

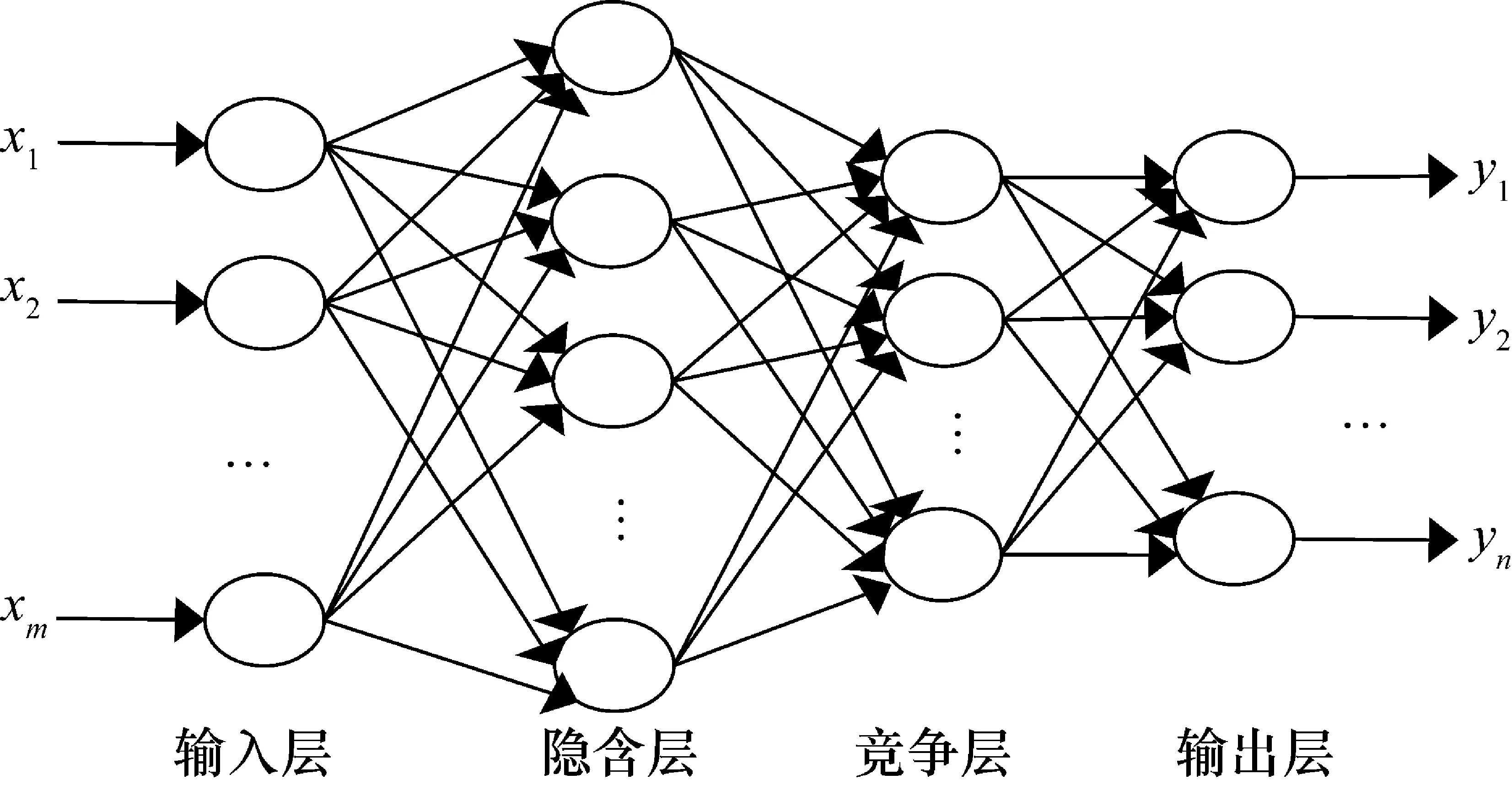
图1 PNN神经网络的结构图

层类别神经元个数输入层负责将特征向量X传入网络,输入层个数是样本特征的个数隐含层隐含层的神经元的个数是输入样本矢量的个数,也就是有多少个样本,该层就有多少个神经元竞争层负责将各个类的隐含层单元连接起来,这一层的神经元个数是样本的类别数目输出层负责输出竞争层中得分最高的那一类

每个隐含层的神经元节点都有一个中心，该层计算输入特征向量与该层中心的距离，并根据这个距离把相关度高的类别集中起来，隐含层的输出值就代表相似度，输出表达式为

(9)

式中，Wi为输入层到隐含层的权值；σ为平滑因子。

PNN神经网络训练时，σ值越大，函数的拟合就越平滑，预测精度就越高，运算速率就越快。反之，若σ值太小，则意味着需要许多的神经元来适应函数的缓慢变化，从而导致网络性能不好。因此合理选择σ值对网络分类性能起到了非常重要的作用[15]。

2.2 LF-PSO算法优化PNN神经网络

LF-PSO算法优化PNN神经网络的流程图如图2所示，算法步骤如下。

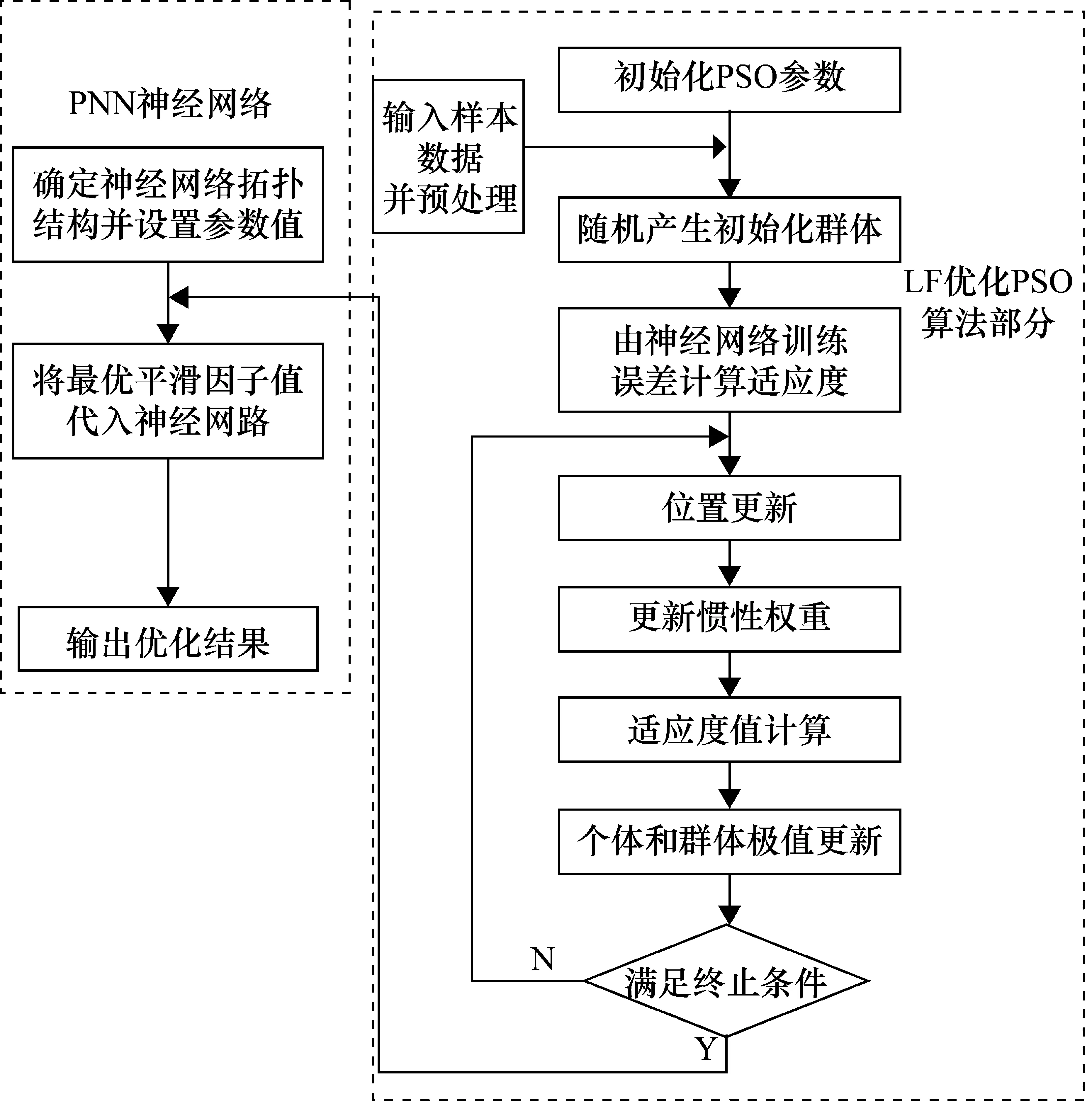
图2 LF-PSO算法优化PNN神经网络的流程图

① 将PNN神经网络的平滑因子作为种群的粒子，给定种群的规模N、最大的迭代次数T，完成种群初始化。

② 初始化种群粒子的位置、个体极值位置和值以及种群极值位置和值，并将每个粒子的最优值存储在pb中，将种群中的最优值存储在gb中[16-17]。

③ 计算各个粒子的适应度值，将PNN神经网络的输出误差作为适应度函数。

④ 根据式(8)更新粒子的位置，根据式(3)更新惯性权重。

⑤ 将粒子的适应度值与其未更新前的位置比较，取较好的粒子为本次迭代后的粒子。

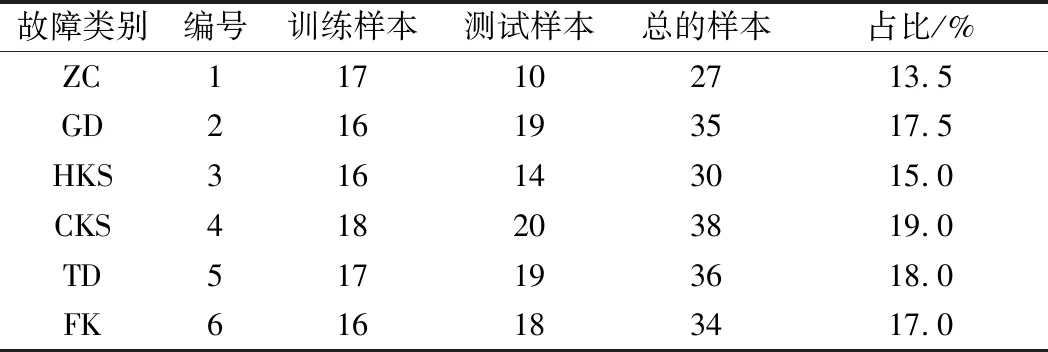
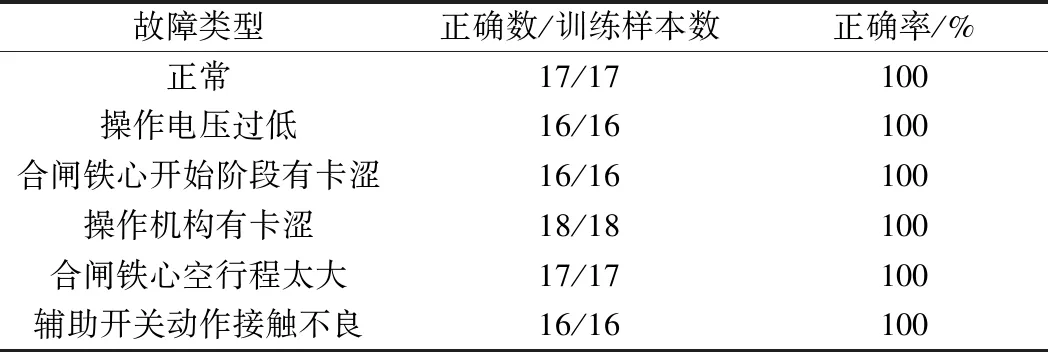
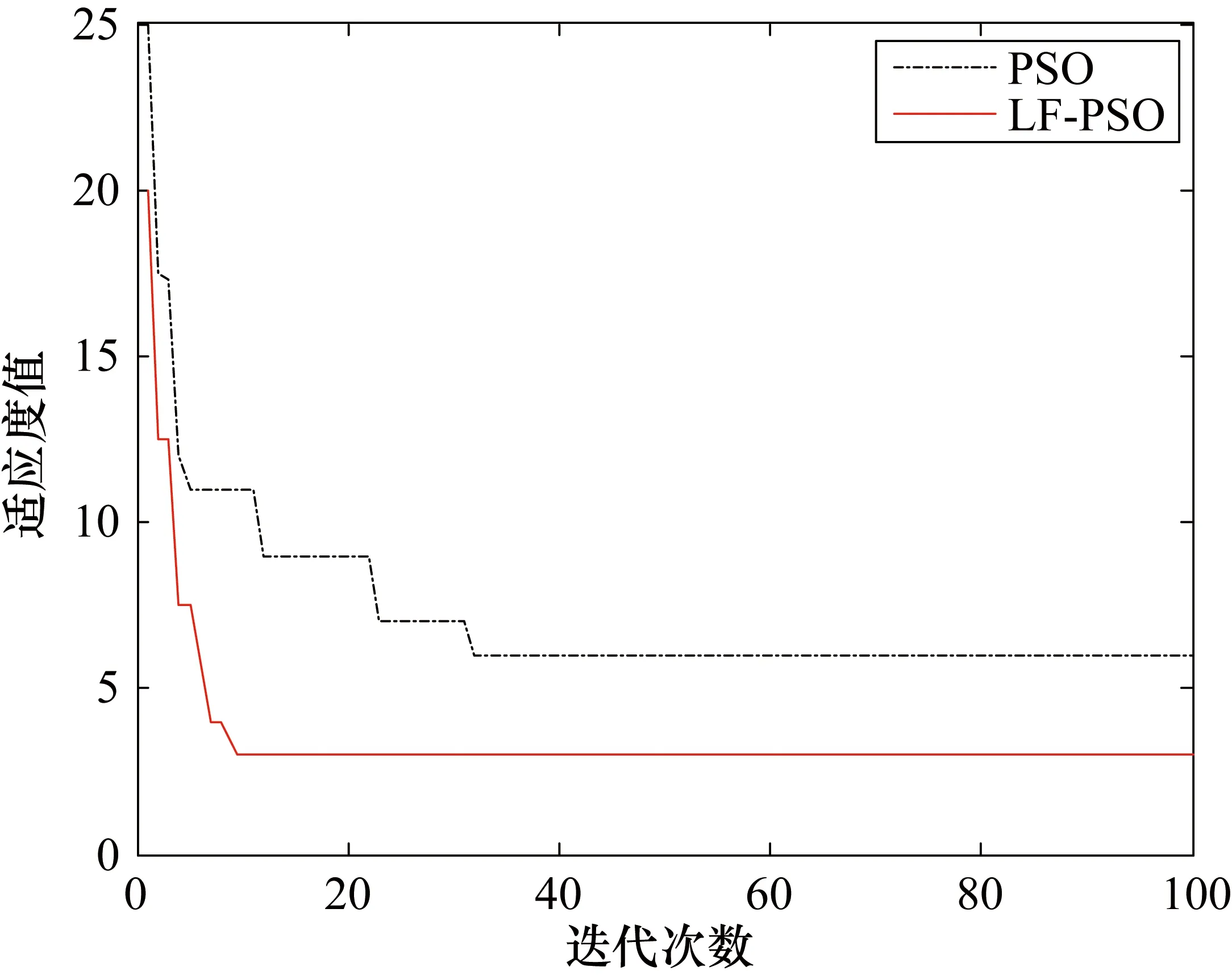
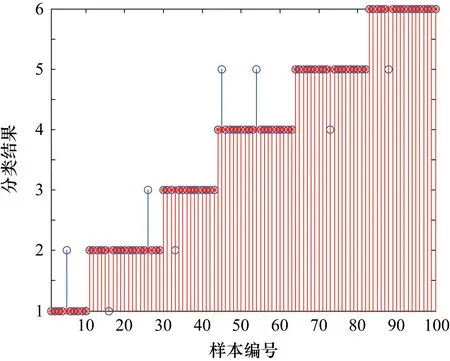
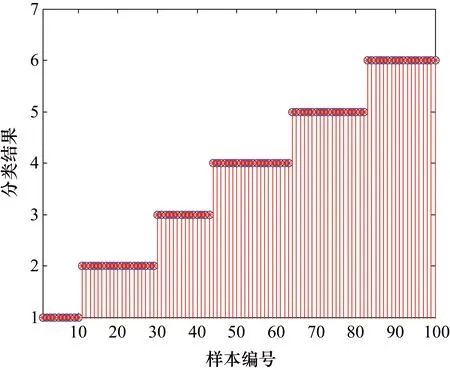
⑥ 比较pb和gb的大小，如果pb

⑦ 若满足迭代结束条件，算法搜索停止;否则返回步骤④继续搜索。

⑧ 将最优的平滑因子代入PNN神经网络中完成测试。

3 实例验证

针对高压断路器的机械特性，选取高压断路器分合闸线圈电流信号中的3个电流量I1、I2、I3和5个时间量t1、t2、t3、t4、t5作为LF-PSO优化PNN神经网络的输入特征值，以正常和5种故障类型操作电压过低(GD)、合闸铁心开始阶段有卡涩(HKS)、操作机构有卡涩(CKS)、合闸铁心空行程太大(TD)、辅助开关动作接触不良(FK)共6类作为输出。

在实验中，PNN神经网络选用8-100-6-6的拓扑结构。现有200组样本数据，一半作为训练数据集，另一半作为测试数据集，数据样本集分组如表2所示。模型基本参数设置为：粒子种群数N设为40；惯性权重ω根据式(3)调整；学习因子c1和c2均设为1.495；β设为1.5；平滑因子的维数均为10；最大迭代次数设置为100。详细参数设置如表3所示。

表2 实验数据样本集

表3 PSO、LF-PSO参数设置

分别用传统PNN神经网络、PSO优化的PNN神经网络以及LF-PSO优化的PNN神经网络对100组高压断路器训练样本进行故障诊断，如表4所示，其中LF-PSO优化的PNN神经网络的故障诊断具体效果如表5所示。为了方便对比不同算法之间收敛速率的差异，图3给出了LF-PSO 算法、PSO 算法在测试数据下的进化过程曲线。随后分别用PSO和LF-PSO优化PNN神经网络对100组测试样本进行诊断，结果如图4和图5所示。

表4 故障诊断正确率

表5 LF-PSO优化算法训练诊断结果

图3 进化曲线

图4 PSO算法测试结果图

图5 LF-PSO算法测试结果图

从图4可以看出，用LF-PSO算法正确率比其他两个方法都高，是可行的。

从图5可以看出，LF-PSO对所列的测试样本的所有故障都能够诊断出来，数据扩大一倍故障诊断可以达到98%，依然比其他两种算法诊断正确率高，验证了该算法在高压断路器故障诊断方面的优势。

综合以上仿真结果，可以分析如下。

① 传统的PNN神经网络平滑因子需要经过反复测试找到合适的值，不适合实际工程；PSO算法对PNN神经网络的平滑因子寻优存在前期搜索精度低、容易早熟收敛的缺点；而LF-PSO算法对PNN神经网络的平滑因子寻优的故障诊断正确率达到100%，高于前面两种方法。

② 对粒子群算法中的惯性权重进行自适应调整，使得粒子群在迭代开始时就有很大的全局搜索能力。

③ LF-PSO算法对高压断路器测试样本诊断正确率达到100%，可以有效实现对高压断路器机械故障的诊断。

4 结束语

本文提出一种LF-PSO算法优化PNN神经网络的方法，首先获得高压断路器分合闸数据集，再利用LF-PSO对PNN神经网络的平滑因子σ进行寻优得到最优参数，最后代入PNN神经网络模型中，实现对其诊断。实验结果表明，该算法优化的PNN神经网络从诊断速度和精度上都要优于传统PNN神经网络和经过PSO算法优化的PNN神经网络。