基于自适应更新策略的蚁群算法在TSP上的应用
2019-10-28
(1.上海工程技术大学 电子电气工程学院, 上海 201620; 2.上海工程技术大学 管理学院, 上海 201620)
TSP属于NP难问题[1],仿生进化思想的发展为NP难问题提供了新的思路,这其中以蚁群算法的贡献最为显著。蚁群算法的提出[2],是源于Marco Dorigo的博士论文,它是一种具有进化思想的启发式算法,根据正反馈机制实现种群间的信息交流。蚁群算法从1992年提出至今,针对该算法的不足,研究学者一直进行着改进工作。Dorigo[3]和T.Stützle[4]分别提出了蚁群系统、最大-最小蚁群算法,对传统蚁群算法的信息素更新方式以及界限进行了改进;文献[5]提出适当刺激蚂蚁尝试那些很少经过的路径,从而增加蚂蚁的全局搜索能力;文献[6]提出信息素二次更新,即在全局信息素更新规则中引入子路径长度的贡献度决策,对下一迭代的τij(t)更新,使那些可能构成全局最优路径的子路径被选择的概率增加,增加算法全局搜索的多样性;文献[5]与文献[6]中算法的收敛速度会随着迭代运行的推进不断变慢;文献[7]引入自适应动态因子σ实时更新全局信息素浓度,自适应动态因子由双曲正切函数f(x)决定,当搜索路径越长,σ越趋近于零,反之亦然,通过f(x)有效区分每次迭代的最优解上的信息素加成影响,加强了较短子路径上的信息素浓度,从而加快算法收敛到全局最优的速度;文献[8]基于精英策略的最大-最小蚂蚁系统,提出加强蚂蚁对已知最短路径的敏感度,让蚂蚁在一个高起点上进行解的优化,该算法前期加快了算法的收敛速度;文献[7]和文献[8]中的算法限制了种群多样性的扩展,算法后期易陷入局部最优;文献[9]保留全局更新中的最短(最长)总路径长度,然后根据约束条件进行增减全局信息素,该算法在处理大规模TSP问题时获得的解精度不高;文献[10]将信息素蒸发参数ρ和信息素值τ相互抑制平衡,这种改进算法增加了全局搜索的多样性,针对大规模的TSP问题,可以获得更好的解质量,但是算法后期的收敛速度还有待提高。
1 相关工作
1.1 TSP问题描述
旅行商问题是旅行者要走遍给定数量的城市,前提这些给定的城市只允许旅行者拜访一次,要求找出旅行者走遍每个城市后的最短路径。一般求解TSP问题的算法分为两大类:精确算法和启发式算法。精确算法主要有定界法、规划法等。启发式算法有遗传算法、模拟退火、粒子群优化算法、蚁群优化算法等。其中蚁群算法由于具备进化思想,为解决旅行商问题提供了新的思路。
1.2 蚁群算法求解TSP问题
在标准的蚁群算法中,蚂蚁根据式(1)[3]状态转移概率规则,判断蚂蚁下一个去往的城市。
(1)
式中,τij(t)为t迭代过程中,城市i与j连接路径上的信息素值;ηij为城市i与j连接路径长度的倒数值,是一种启发式信息,如果城市i与j连接路径长度越短,那么蚂蚁选择的下一个城市越可能是j;Allowedk为蚂蚁k未走过的城市;α和β分别决定了信息素和启发因子的重要性。当所有蚂蚁完成了一次完整的路径构建,即完成一次迭代,此时信息素的更新将会按照式(2)[3]进行。
(2)
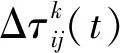
2 改进算法
2.1 自适应局部信息素更新方式
文献[2]~文献[4]的局部信息素更新都是根据式(3)[3]进行的。
τij(t+1)=(1-ρ)τij(t)+ρΔτij(t)
(3)
式中,ρ为信息素挥发参数[3],取值范围在[0,1]。这些传统算法一直把ρ设置为定值,但是随着TSP问题规模的改变,就需要不停地通过实验去寻找合适的定值,无疑增加了解决TSP问题的时间,解质量也没有太大的改善。所以提出式(4)以自适应地改变信息素挥发值。
ρ=kτij(t)
(4)
式中,k为一个比例因子,在这里设置为0.5。这样信息素挥发值ρ就会自适应地在[0,0.5]间取值,一开始路径上的信息素值很小,这样ρ的取值也会取较小值,使得路径上的信息素挥发量很少,从而蚂蚁释放在路径上的信息素保存量就会增加,加快算法收敛到最优路径上,随着算法不断的迭代运行,此时路径上的信息素就会不断增加,这样ρ的取值也会相应增大,使得路径上的信息素挥发量增加,上一代蚂蚁释放在路径上的信息素量就会减少,这有助于算法跳出局部最优,增加了路径选取的多样性,避免了算法过早地收敛或停滞,从而很好地平衡蚂蚁探寻新的路径和强化已找到的算法最优路径。
2.2 改进的全局信息素更新方式
在计算经过一次迭代过程所有蚂蚁构建的总旅行长度时,求出本次迭代里的最短总旅行长度和最长总旅行长度,然后对蚂蚁寻找到的最短和最长总旅行路径上的全局信息素根据式(5)进行更新。
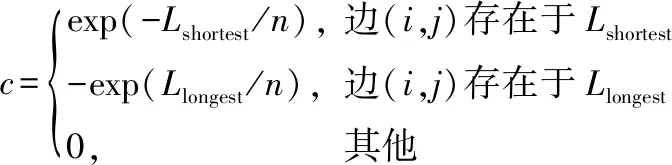
(5)
式中,Lshorlest(llongest)为蚂蚁找到的全局最短(长)总旅行路径长度;n为城市总个数,引入城市个数,阻止因TSP规模增大使c值趋于零,奖惩机制作用力下降。这里改进的全局信息素更新策略是通过奖励(惩罚)当前最好(最差)总旅行路径上的信息素,在强化当前迭代找到的全局最优解的同时又削弱最差解对蚂蚁路径选择的影响来实现的。因为使用的是以指数函数的形式进行增减全局信息素的方法,较反比例函数增减幅度更小一些,这样TSP问题中各路径上的信息素值差距就不会很大,某种程度上给予蚂蚁更多路径选择权,在加快算法收敛到最优解的同时有效预防了算法过早收敛停滞。
2.3 改进的子路径贡献度
基本的蚁群算法在全局信息素更新中,蚂蚁会增加找到的最优路径的信息素值,然而在最优路径里某些子路径过长时,蚂蚁就会去增强子路径较短的路径,而这些路径可能不属于全局最优解,这样会造成局部最优的困境。为了改善这种情况,根据式(6)、式(7)提出改进的子路径贡献度的概念,在当前迭代最优解中,找出子路径对全局最优路径贡献值大于路径本身贡献度值的所有子路径,然后对这些子路径一一进行信息素再强化处理,更新公式如下:
lij=d(i,j)/[Lbest(t)-d(i,j)]
(6)
(7)
(8)
在对当前迭代最优路径上的信息素更新后,再根据式(6)计算构成当前迭代最优路径的子路径贡献值,q0是一个阈值,这里设置为0.3。式(7)表示满足判别条件的子路径上信息素强化增量,然后根据式(8)调节子路径上的信息素终值。
2.4 AU-ACS算法流程
采用AU-ACS算法求解旅行商问题的基本步骤如下。
1:INPUT:none
2:OUTPUT:length_best % best solution at any time
3:t=0 % iteration count
4:kib% iteration best ant
5:τ0% initial pheromone trail
6:Nmax% maximum number of iterations
7:parameter initialization
8:while (termination condition not satisfied) do
9:ConstructSolutions
10:length_best←The current iteration finds the best length
11:Local pheromone updates %using Eq.(4)
12:Global pheromone update % using Eq.(5)
13:Path quadratic optimization % using Eq.(6)-(8)
14:Local search optimization % using the 3-Opt algorithm
15:t←t+1
16:if (t≥Nmax) then
17:Terminate program run
18:end while
19:if (the solution didn’t improve very long) then
20:initializes the parameters and rerun the program
21 end
3 仿真实验与结果分析
为验证提出的AU-ACS算法的理论有效性,选取了TSPLIB(http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/STSP.html)里的典型问题集,在CPU为i5-4200M、RAM为8 GB的PC上用Matlab仿真测试,将AU-ACS算法和ACS算法、MMAS算法(均加入了3-Opt算法)的实验结果进行对比,直观地得到AU-ACS算法的改进效果。本文算法的基本参数设置如表1所示。

表1 AU-ACS算法的基本参数配置
3.1 问题求解及对比
如图1所示,以eil51为实验对象,对ACS算法添加各类改进方式进行仿真,ACSL、ACSQ、ACSZ、AU-ACS分别是ACS算法添加了自适应局部信息素更新方式、改进的全局信息素更新方式、改进的子路径更新方式、3种改进方式+3Opt[11]算法。如图1所示,可以看出ACS算法只添加自适应局部信息素更新方式,提高了算法搜索的多样性,但是算法迭代收敛到最优解的速度缓慢;只添加改进的全局信息素更新方式,提高了算法收敛到最优解速度,但是种群多样性不高,进而解精度较差;只添加改进的子路径更新方式,随着算法的迭代运行,提升了解的精度;最后把3种改进方式与3Opt算法结合到ACS算法中进行仿真,可以看出既增加了种群多样性,又加快了算法的收敛到最优解的速度。
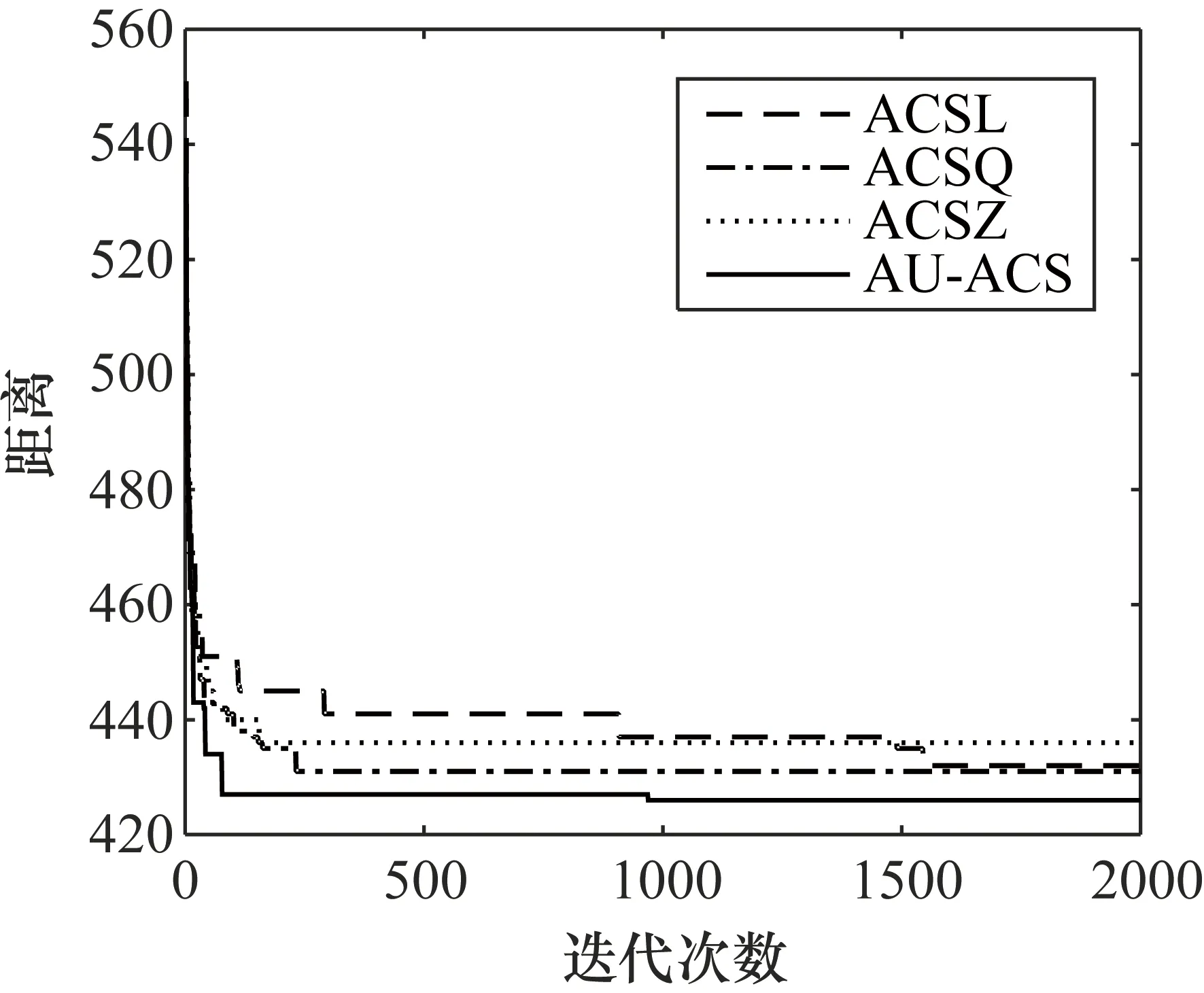
图1 ACS添加不同改进方式的仿真结果
选取eil51、eil76、kroA100、kroB150,用AU-ACS、ACS、MMAS这3种算法进行实验,各自实验20次。对3种算法的仿真结果进行对比,如图2所示,在设置的3个TSP问题案例中,AU-ACS算法都可以找到问题已知最优解,分别是:426、538、21282、26130。基于eil51案例中,在前200次的迭代过程里,相对于ACS、MMAS算法,AU-ACS算法收敛的速度更快,并且收敛的精确度也更高,在经过500次迭代后,AU-ACS已经收敛到了已知最优解;基于kroA100案例中,相对于ACS、MMAS算法,AU-ACS算法收敛速度超快,大约在经过70次迭代后,AU-ACS就已经收敛到了已知最优解;基于kroB150案例中,相对于ACS、MMAS算法,在前400次的迭代过程,AU-ACS的收敛速度更快,虽然ACS算法经过400次迭代后收敛速度略快于AU-ACS算法,但是ACS算法最终却没有找到案例已知最优解,MMAS算法虽然在早期迭代过程中不断向已知最优解收敛,但是在经过600次迭代后,算法陷入了局部最优解,削弱了算法寻找更优解的能力,算法的多样性由此降低,AU-ACS算法在1500次迭代后快速收敛于已知最优解,从而凸显了AU-ACS的优越性。
3种算法在几类TPS问题中的结果比较如表2所示。

图2 AU-ACS和ACS、MMAS算法在几类TSP问题中的迭代情况
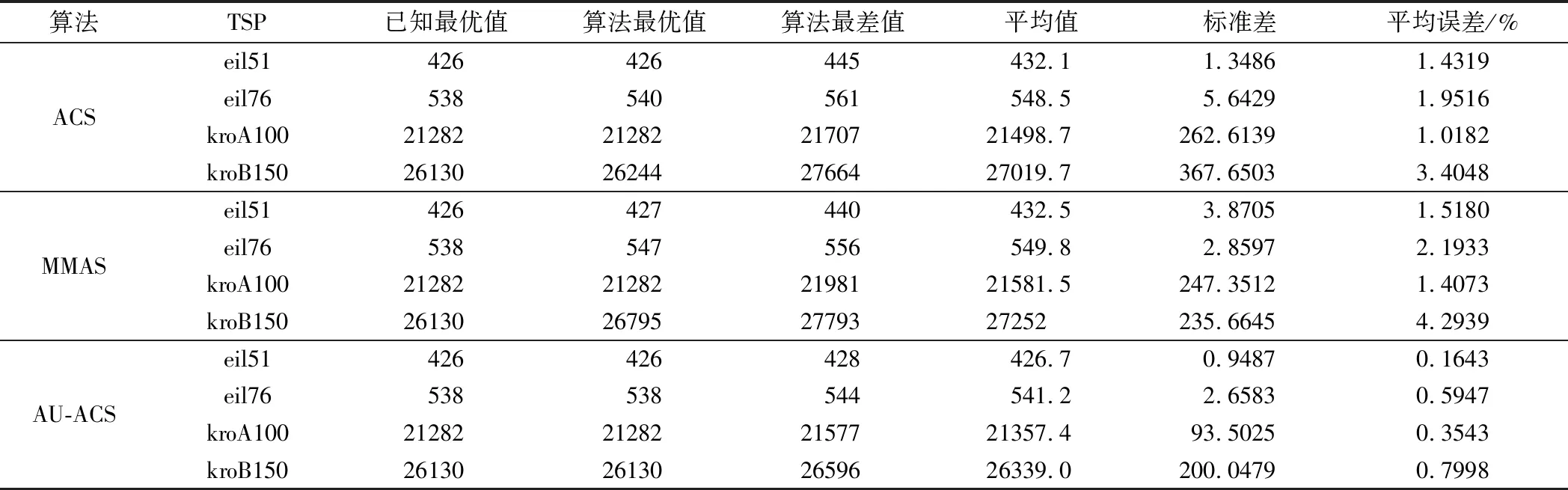
算法TSP已知最优值算法最优值算法最差值平均值标准差平均误差/%ACSeil51426426445432.11.34861.4319eil76538540561548.55.64291.9516kroA10021282212822170721498.7262.61391.0182kroB15026130262442766427019.7367.65033.4048MMASeil51426427440432.53.87051.5180eil76538547556549.82.85972.1933kroA10021282212822198121581.5247.35121.4073kroB15026130267952779327252235.66454.2939AU-ACSeil51426426428426.70.94870.1643eil76538538544541.22.65830.5947kroA10021282212822157721357.493.50250.3543kroB15026130261302659626339.0200.04790.7998
如表2所示,对比算法找到的解质量、平均值、标准差、平均误差(平均值与算法已知最优值的差值除以算法已知最优值),AU-ACS算法都更加优越、稳定。以kroA100为例,3种算法虽然都找到了案例已知最优解,但是就平均值而言,AU-ACS算法更接近已知最优解值,从平均误差而言,AU-ACS算法比ACS算法低了0.6639%,比MMAS算法低了1.053%;如图2所示,AU-ACS算法在490次迭代收敛,比ACS算法快了269,比MMAS算法快了408。可以看出,AU-ACS算法不管是收敛精度还是收敛速度都更具备优越性。以kroB150为例,只有AU-ACS算法找到了问题已知最优解,从标准差而言,AU-ACS算法比ACS算法小167.6024,比MMAS算法小35.6166;从平均误差而言,AU-ACS算法比ACS算法低了2.605%,比MMAS算法低了3.4941%。所以AU-ACS算法具有更好的稳定性。
3.2 AU-ACS算法找到的TSP问题路径图
AU-ACS算法找到的几类TPS问题路径图如图4~图7所示。采用AU-ACS算法优化路径,eil51、eil76、kroA100和kroB150这4种TPS的最短距离分别为426,538,21282,26130。
4 结束语
针对蚁群算法存在的过早收敛、搜索时间长的问题[12-15],提出了具有自适应信息素更新策略的蚁群算法,改进的自适应策略包括:自适应局部信息素更新方式、改进的全局信息素更新方式、改进的子路径贡献度等,这些改进策略相互作用共同提高本文算法的性能。实验结果表明,AU-ACS算法的最优解精度和算法收敛速度都比ACS算法和MMAS算法更优越,并且,随着选择的TSP案例的城市规模越大,显示出的优势越发明显。在接下来的研究过程中,将进一步研究自适应信息素更新策略,从而进一步改进蚁群算法在TSP问题上的应用。
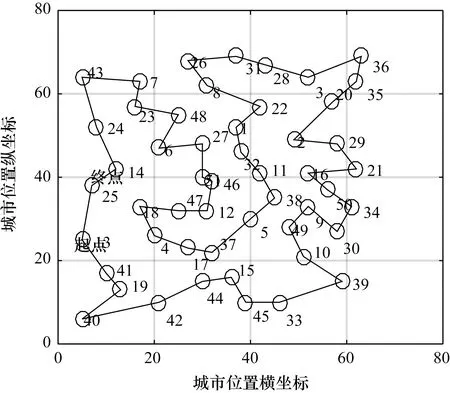
图4 eil51路径图
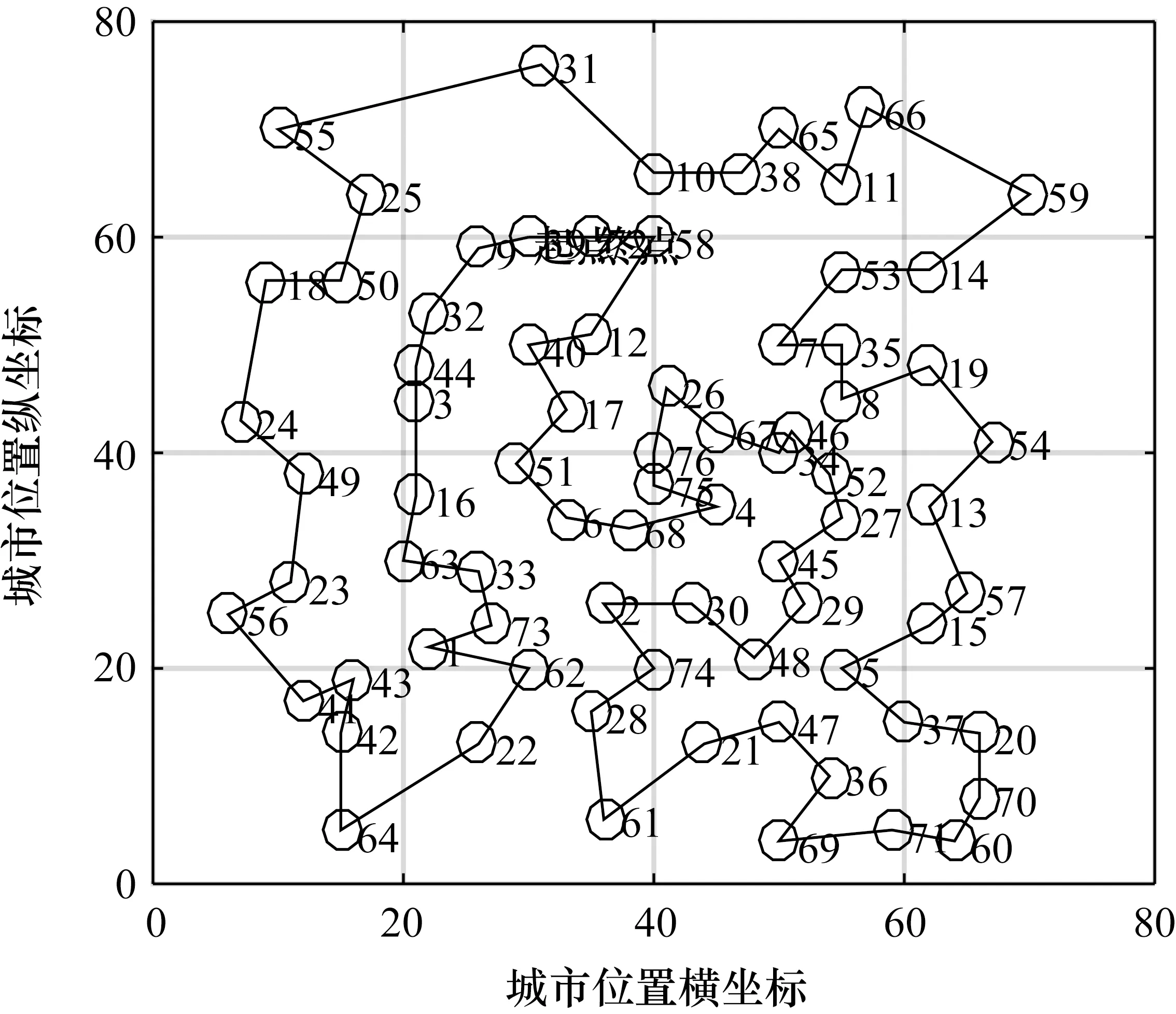
图5 eil76路径图
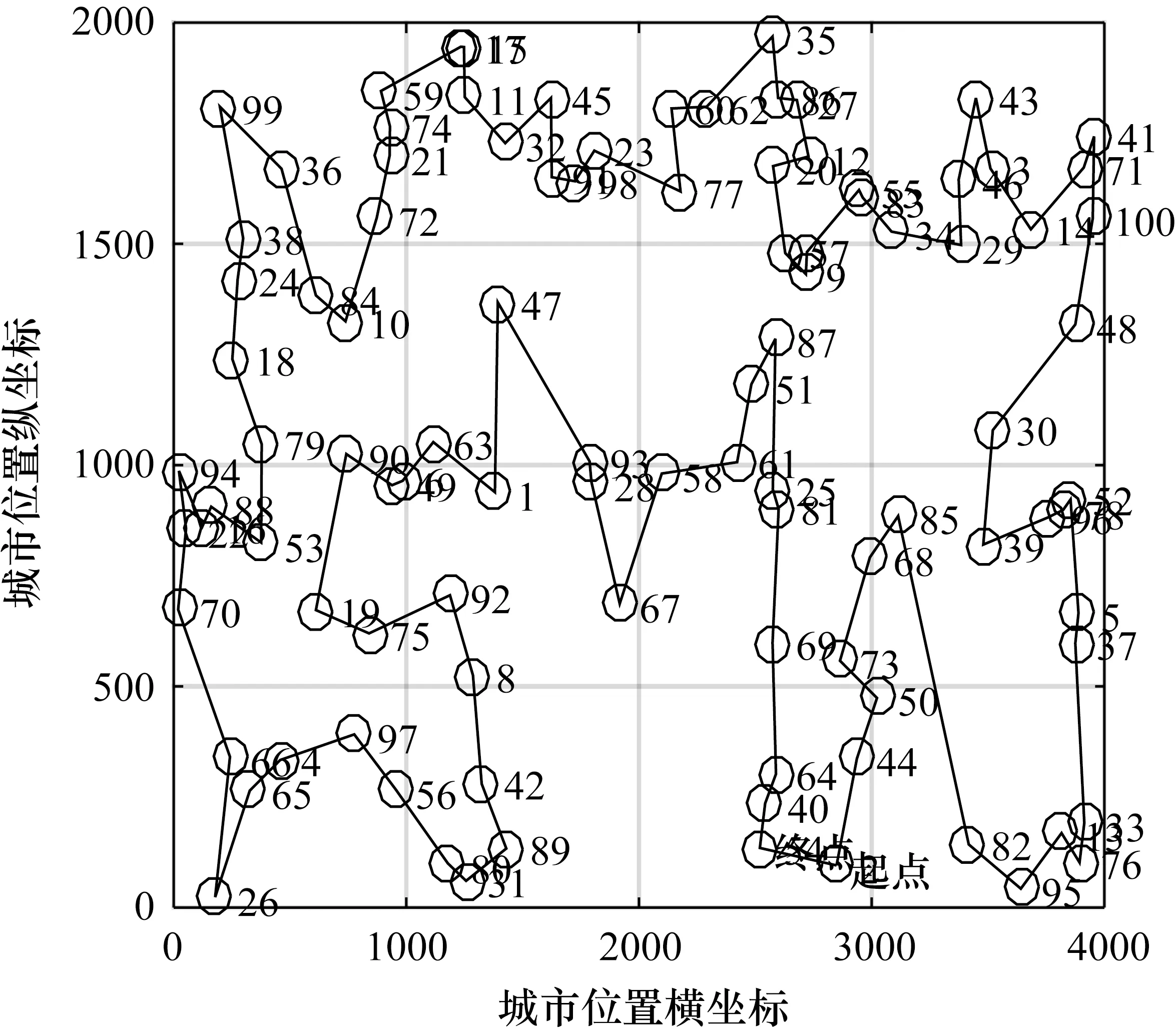
图6 kroA100路径图

图7 kroB150路径图
