基于物联网节点加权的D-S证据理论数据融合算法

杨呈永,刘佳祎

(桂林理工大学 现代教育技术中心, 广西 桂林 541006)

物联网的概念最早可追溯到1999年, 由Kevin等提出。 国际电信联盟(international telecommunication union,ITU)在2005年11月的报告中对“物联网”的概念和特征[1]以及未来发展过程中将面临的困难等方面进行论述，并将相关成果发布到《ITU Internet reports 2005—The Internet of Things》中。 为了达到人与物相交互的目的, 人们利用如无线传感器、 RFID、 GPS 等设备将现实中的物品进行网络连接, 并将这一过程称为物联网[2]。 基础设施的不断完善使得物联网核心技术也得到了快速发展, 并在日常生活的各个方面得到应用。 由于不同的应用服务商监测的目标各不相同, 进而产生了数量巨大的待处理监测数据, 如果不能及时高效地处理, 将会在网络传输过程中造成严重的带宽资源浪费。 由于物联网的各个节点的工作状态不能够保证稳定, 所以物联网的数据存在着严重的不确定性问题。

信息融合作为可以把所获取的多源信息对比、分析和评估后得到的有效信息进行融合处理的一种热点技术,具有更加精确、更加全面的判别力，深受学者们的青睐[3-4]。目前,国内外研究学者针对D-S证据理论[5]这一热点信息融合技术的研究主要有:利用数学模型修正证据源的冲突证据合成方法[6-7];徐琰珂等将模糊逻辑算法进行优化用于提高信息融合系统的稳定性[8];文献[9-11]中重点介绍贝叶斯网络和层次分析法等算法与原D-S证据理论的结合;如何用D-S证据理论解决某一具体应用中存在的问题[12-15]。

通过上述文献可发现，在D-S证据理论中的单一问题，学者们作了良好的改进与分析,且在D-S证据理论的实际应用中,人们常常只关注融合后的最终结果,并不关注事件本身的特征,这样会造成底层融合数据特征的流失。因此,如何在融合过程中,对事件进行多维度的分析成为目前急需解决的重点问题。

1 常见融合算法

数据融合是一种将多源数据进行融合处理的技术, 是智能信息处理技术的范围。 通过将各个节点的数据进行充分分析和整合得到对监测对象的最佳一致估计, 比单一的数据源更为精准、 全面[16], 从而使用户作出正确的选择。 数据融合算法经过多年的发展, 有一些算法形成了比较成熟的方法, 还有一些算法是学者研究的热点。 常见的数据融合方法主要有: 古典概率推理、 贝叶斯方法、 神经网络、 模糊集理论、 D-S证据理论。

1)古典概率推理。古典概率讨论的范围仅限于随机试验产生的等可能结果的情形[17]。每次试验有有限个结果,而且结果出现的可能性一致。缺点是无法直接应用先验知识,一次只能评估两个假设事件等。

2)贝叶斯方法。贝叶斯(Bayes)发展的比较早,该方法是基于最大后验和似然比检验,如果先验概率能够算出,贝叶斯方法将是一个很好的解决方法。但是在实际问题求解中很难获得先验概率,即确定先验的似然函数非常困难。而且,传统的贝叶斯要求条件复杂苛刻[18]，很难满足和实现,这就限制了贝叶斯的应用。贝叶斯也无法处理广义的不确定问题。

3)神经网络。近年来以神经网络(neural networks)进行数据融合的技术取得了很大的进步[19]。神经网络的工作原理和人类大脑类似,模拟人脑的思维,该算法具有简单的并行分布式计算、平行分布式处理(速度快)、容错性高、数据鲁棒性等特点。神经网络允许多个信号的输入和多个变量的输出,经过系统训练,把数据分配到正确的分类中输出,适合多变量系统。神经网络可以在训练过程中输入没有出现过的新数据,并进行识别,因此该算法可以进行学习和自适应。通过神经网络的学习,可以很好地适应无数学模型和难以建立数学模型的推理过程。神经网络的神经元一般是线性的,要处理复杂的非线性问题,还需要进一步的改进和发展。此外,神经网络的输入数据若不是很充分,将不能够正常工作,这也是一个局限。

4)模糊集理论。模糊集(Fuzzy Sets)理论在模糊集的基础上发展起来,由于具有处理模糊问题的能力和模糊推理的优势,被广泛地应用于信息融合领域[20]。模糊理论和模糊逻辑也被应用到多源数据融合技术中。模糊集将数据元素与集合关系的绝对化处理为模糊概率化。源数据在模糊集处理之前只有存在或不存在集合两种关系,经过模糊运算处理之后,表示为源数据在集合中存在概率的多少,然后用一定的方法统一融合决策。

5)D-S证据理论。Dempster于1967年提出了证据理论，Shafer把该理论推广到更一般情形。D-S(Dempster-Shafer)证据理论在贝叶斯的基础上作了推广,引入信任函数的概念,借助了多重证据来确定决策结论。通过给命题(如今天的气温)分配一定的信任函数,对多个问题的不精确描述有效分析后,再利用相应的公式将矛盾数据有效排除和整合,便可得到确定数据。同传统的数据融合方法相比,D-S证据理论最大的特点是以证据的形式来表现数据的不确定性,且证据理论摆脱了贝叶斯理论对先验知识的依赖。D-S证据理论的不确定性推理过程可以解决物联网节点产生的不确定性数据,对数据进行融合运算,得到较为确定的数据[21-22]。

本文以D-S证据理论为基础, 研究在物联网环境下, 如何更好解决数据的不确定性问题。

2 D-S证据理论用于数据融合的基本概念及分析

1967年,为纪念A.P.Dempster和G.Shafer两位学者在证据理论方面作出的突出贡献,人们将证据理论称为Dempster-Shafer理论。

2.1 识别框架

用Φ集合来表示已了解的情况下所有可能出现的判决结果的集合。如果Φ中的任一个子集表示人们所关心的任一命题,则称Φ为识别框架。

2.2 基本可信度分配与信度函数

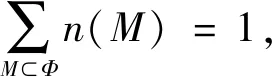
设Φ代表一个识别框架信度集函数A: 2Φ→[0,1]必须同时满足3个条件:A(O)=0;A(Φ)=1;当∀M1,M2,…,Mt⊂Φ时,有

(1)

由式(1)可知,D-S证据理论在整个框架中都存在不确定的信度。

2.3 似真度函数

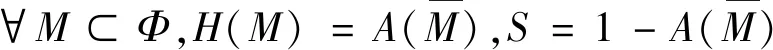
2.4 Dempster合成法则

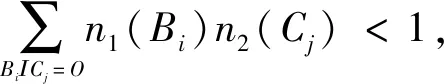
当M≠O时,

(2)

当多个信度函数A1,A2,…,Ai在同一框架Φ上时，它们所对应的基本可信度分配分别为n1,n2,…,ni。 假设∀M⊂Φ,M≠O且A1⨁∧⨁An存在基本可信度分配，用n表示,则有:

(3)

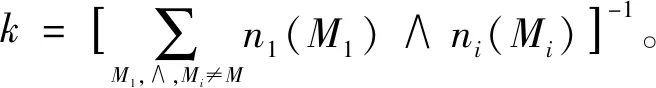
由式(2)和式(3)可知，无论有多少个证据，相结合次序都不会影响其结果，可以用两个证据的计算来递推得到多个证据结合的计算。

3 基于物联网节点加权的D-S证据理论数据融合算法

3.1 基于物联网节点的D-S数据融合方法

对于物联网节点的数据融合来说,将物联网中的各个节点看成一个命题，则具有识别、判断及处理等功能的传感器所展示的结果即为该命题对应的证据。若想要将物联网中多个节点的数据进行融合时,则将采集到的数据进行度量，然后建立相应的基本概率分布函数作为可信度指标。各个函数和对应的框架称为一个证据体,故在物联网节点中每个传感器都是一个证据体。利用Dempster合并规则在同一个框架下将每个证据体组合成完整的证据体,这就是物联网节点数据融合的本质。图1展现了基于物联网节点的D-S数据融合方法，其中,n1(Mj),n2(Mj),…,ni(Mj)为i个节点的基本可信度分配；j=1,2,…,n；n(Mj)为经过Dempster合成法则结合成的新的基本可信度分配。

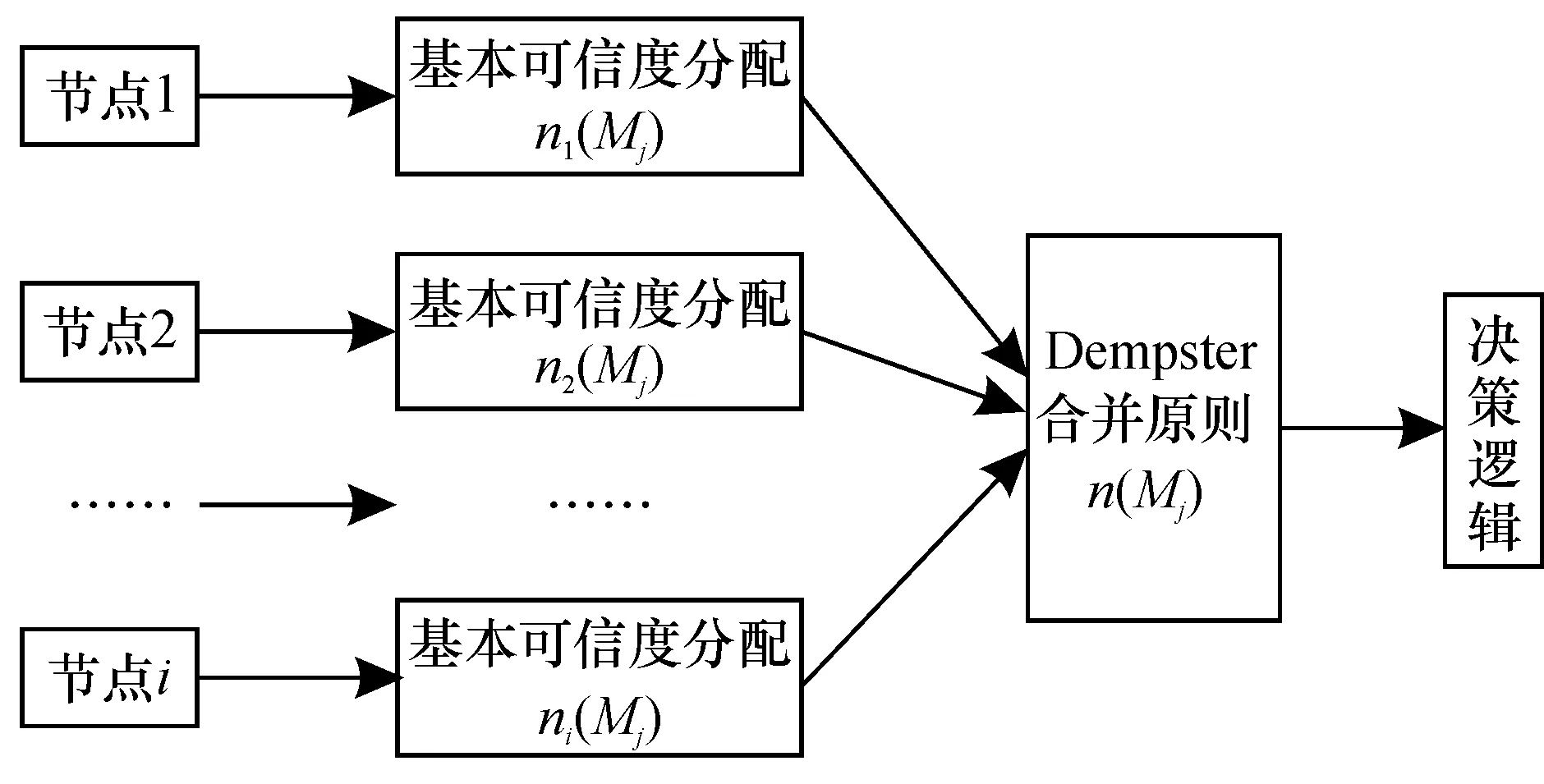
图1 基于物联网节点的D-S数据融合Fig.1 D-S data fusion based on IOT nodes

在物联网各节点中多个传感器系统的数据融合中,首先对系统进行第一次基本可信度分配，传感器每一次报警,节点就会发送一个具有可分配的基本可信度；然后根据图1中的法则将这些基本可信度进行合并得到最终结果；最后根据可信度和似真度等指标来判断命题的合理性,将决策结果输出。

3.2 多物联网节点系统的D-S数据融合结构

在多个节点数据融合中,庞大的数据量使传统的计算方式难以适用,设A为n个证据结合计算后的结果,1～n为n个证据,采用两个证据结合的计算方法递推出n个证据结合的计算，如图2所示,其中,左侧为传统的直接计算,右侧为递推n个证据结合的计算。

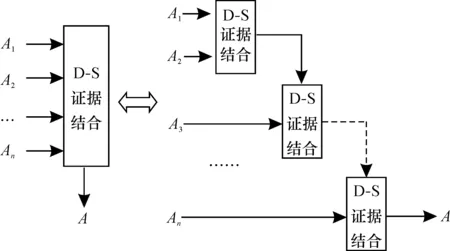
图2 多个证据等效结构图Fig.2 Equivalent structure of multiple evidences

3.3 根据冲突情况调整节点权重大小

因为物联网的节点监测能力不同,发送数据的可靠性不同,节点的能耗也不同。如果某一个可靠性高的节点突然发生了故障,导致节点发送的数据产生了很大的误差，此时，在融合的过程中如果还按照原来的权重进行基本概率分配,就会产生与实际情况不符的错误。因此,本文在原有节点权重的基础上再进行一个权重的修改,在数据融合的同时考虑节点能力大小和节点冲突性。当一部分数据与其他大部分数据存在较大的冲突时, 即使这个节点的能力很大, 权重很高, 也认为这一部分数据可能会不准确, 将会相应地对该权重进行微调, 尽量使这些不精准的数据对结果没有过多影响。 弱化坏的数据对最终决策的支持, 在一定程度上优化最终融合结果。

假设有识别空间Φ={M1,M2,…,Mn},其中M1,M2,…,Mn是各种假设,证据集合E={E1,E2,…,Em},每个证据对应的权重集合为W={w1,w2,…,wm}。每个证据的冲突ki情况按照D-S证据理论的冲突概率大小定义为

(4)

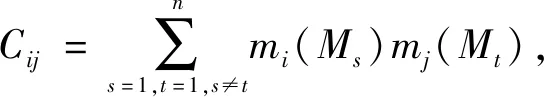
得到每个证据的冲突概率状况后,根据每个证据的冲突概率和整个识别空间的冲突概率对比,再进行权重调整。整个识别空间的冲突概率表示为

(5)

这时引入原来的节点权重,根据冲突概率的大小来决定权重总量W

W=m×k0×wmin,

(6)

其中,wmin是原权重中的最小值。这里的权重总量考虑了冲突状况。

根据权重总量作调整,原有的权重大小减去权重总量的平均数，也就是每一个证据的权重减去了冲突部分的权重：

(7)

最后调整权重的大小,节点的权重大小表示为

(8)

基于节点加权的D-S证据理论方法的步骤为

输入:待融合目标M={M1,M2,…,Mn},n个节点的信任度函数ni(M)以及相应节点权重wi,初始化i=1。

输出:融合目标的结果。

步骤:

①计算每一个证据ni(M)的冲突概率ki,根据冲突概率调整相应的基本概率分配,得到新的基本概率分配。

②计算n1(M)和n2(M)的冲突系数K。当K≠1时,调用D-S证据融合公式进行数据融合得到融合数据n(C)。

③循环n-2次。计算n(C)和ni+2(M)的冲突系数K。当K≠1时,调用D-S证据融合公式更新融合数据n(C)。

④循环结束,得到最终的融合结果n(C)。

4 实验与结果分析

为验证物联网中数据传输的不确定性，本文选择物联网中节点1、2、3、4这4个节点，在Windows XP操作系统的电脑上采用NS2仿真软件进行模拟仿真实验。假设在一个盒子中有且仅有3种颜色的球:红、黄、绿,记在盒子里取出球的颜色种类{红球、 黄球、 绿球}为监测目标,表示为A、B、C，则这4个节点分别对应的信任函数为m1,m2,m3,m4。

通过NS2仿真软件可得到一组有效数据,4个节点的权重值分别为0.1,0.2,0.5,0.2。对监测目标{红球、黄球、绿球}的信任度分别为:

m1(A)=0.1,m1(B)=0.8,m1(C)=0.1;

m2(A)=0.2,m2(B)=0.7,m2(C)=0.1;

m3(A)=0.8,m3(B)=0.1,m3(C)=0.1;

m4(A)=0.1,m4(B)=0.7,m4(C)=0.2。

由上述数据可得基本概率分配(表1)。

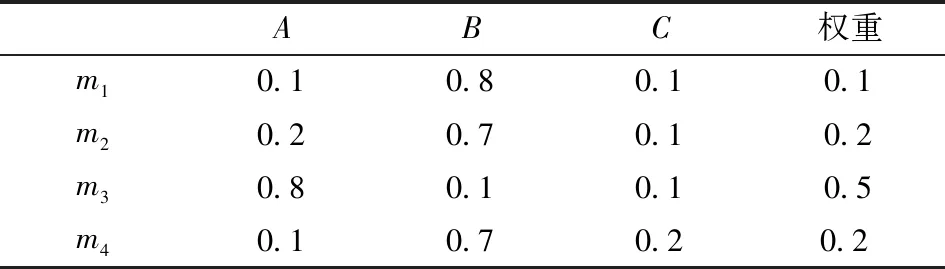
表1 四个节点的概率分配

根据本文提出的证据理论方法,系统得到最终的基本可信度分配；然后根据可信度和似真度等指标来判断命题的合理性,将决策结果输出；最后按照传统的D-S证据理论公式合成最终的数据结果。根据节点的权重计算最后的融合数据为{0.142, 0.782, 0.085},其结果为黄球。

为了检测不同节点权重下的D-S证据融合理论的结果,将4个节点中的一个去掉，变成节点1、2、3这3个节点,监测目标的信任函数分别为监测目标红球A、黄球B、绿球C。通过NS2仿真生成相关数据(表2)。

表2 不同节点权重下两种方法的比较

可以看出, 传统的D-S证据理论不考虑节点的性能，只是依照证据进行数据融合, 不适用于物联网这种大的环境。而基于节点加权的D-S证据理论能够充分将数据节点的可靠性、节点性能的大小，以及自身发出数据与其他节点发出数据的冲突等综合考虑。其结果说明D-S方法在目标识别及节点加权的数据融合中最大程度支持正确结果。

为进一步检测D-S方法在目标识别及节点加权的数据融合中最大程度支持正确结果,本文采用文献[22]中使用的数据集进行测试,选取该数据集中的6类,共211 570个网络流样本,图3有效展示数据集属性的分布情况,算法的检测概率和虚警概率如图4、图5所示。

在物联网底层中具有大量的数据节点,由于环境等因素的影响导致很多传输数据具有不确定性,将数据进行加权有效降低数据融合后的不确定性,由上述两图可知,算法突出了对样本的识别判断能力,在采用节点加权样本数据的情况下,可以有效识别判定出被观测对象的属性。虽然其检测概率略低于不含节点加权样本数据的情况,但是虚警概率明显较低。由此可证明,基于物联网节点加权的D-S证据理论数据融合算法在较低虚警概率下具有较好的检测概率。

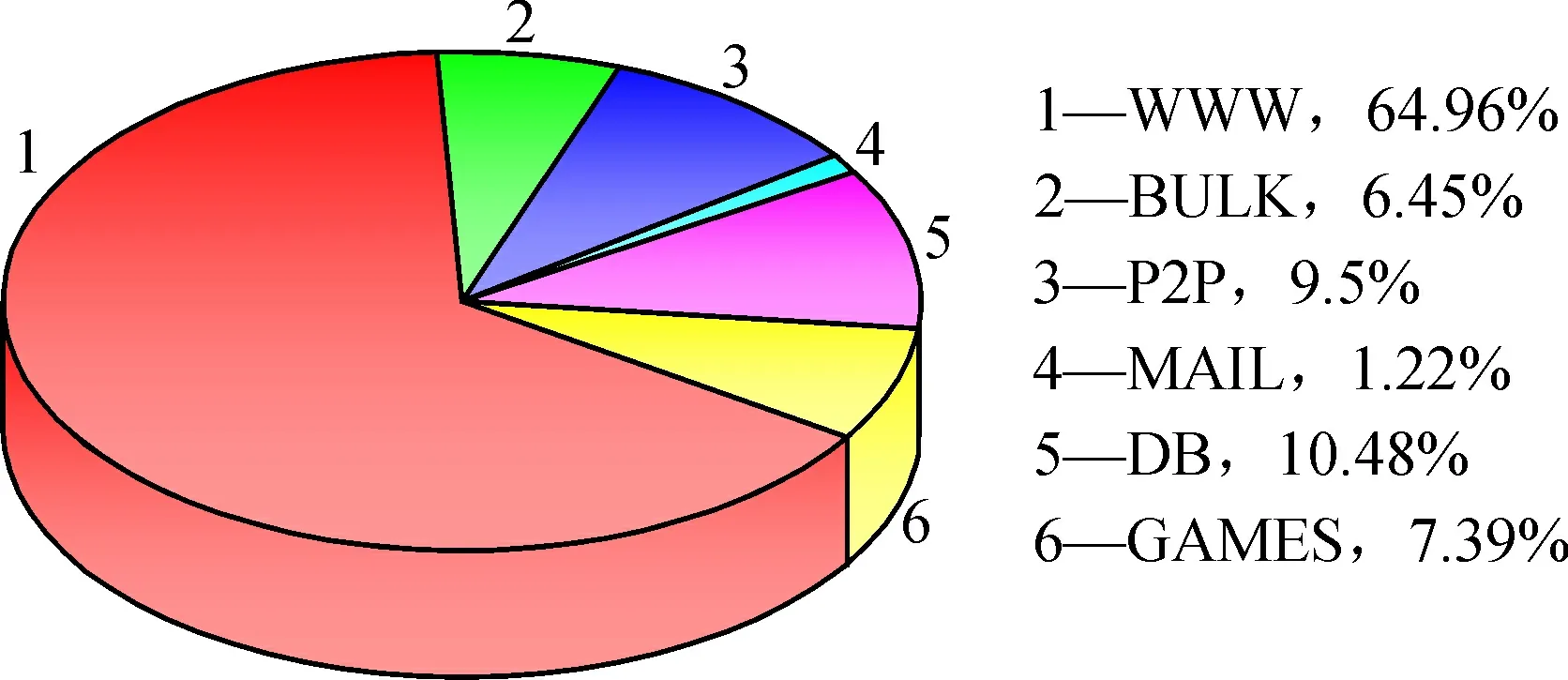
图3 数据集属性分布Fig.3 Data set attribute distribution

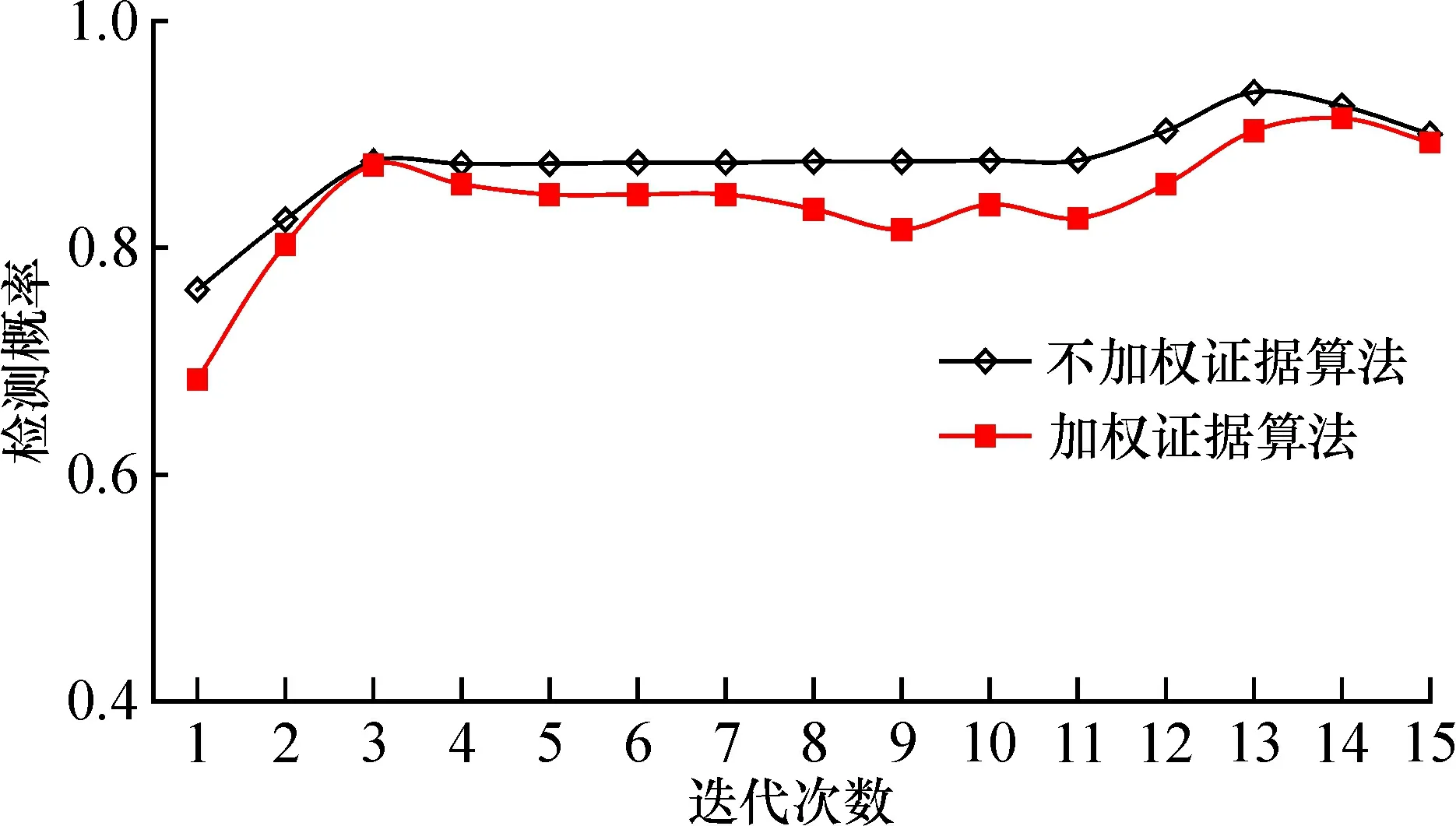
图4 算法的检测概率Fig.4 Detection efficiency of the algorithm

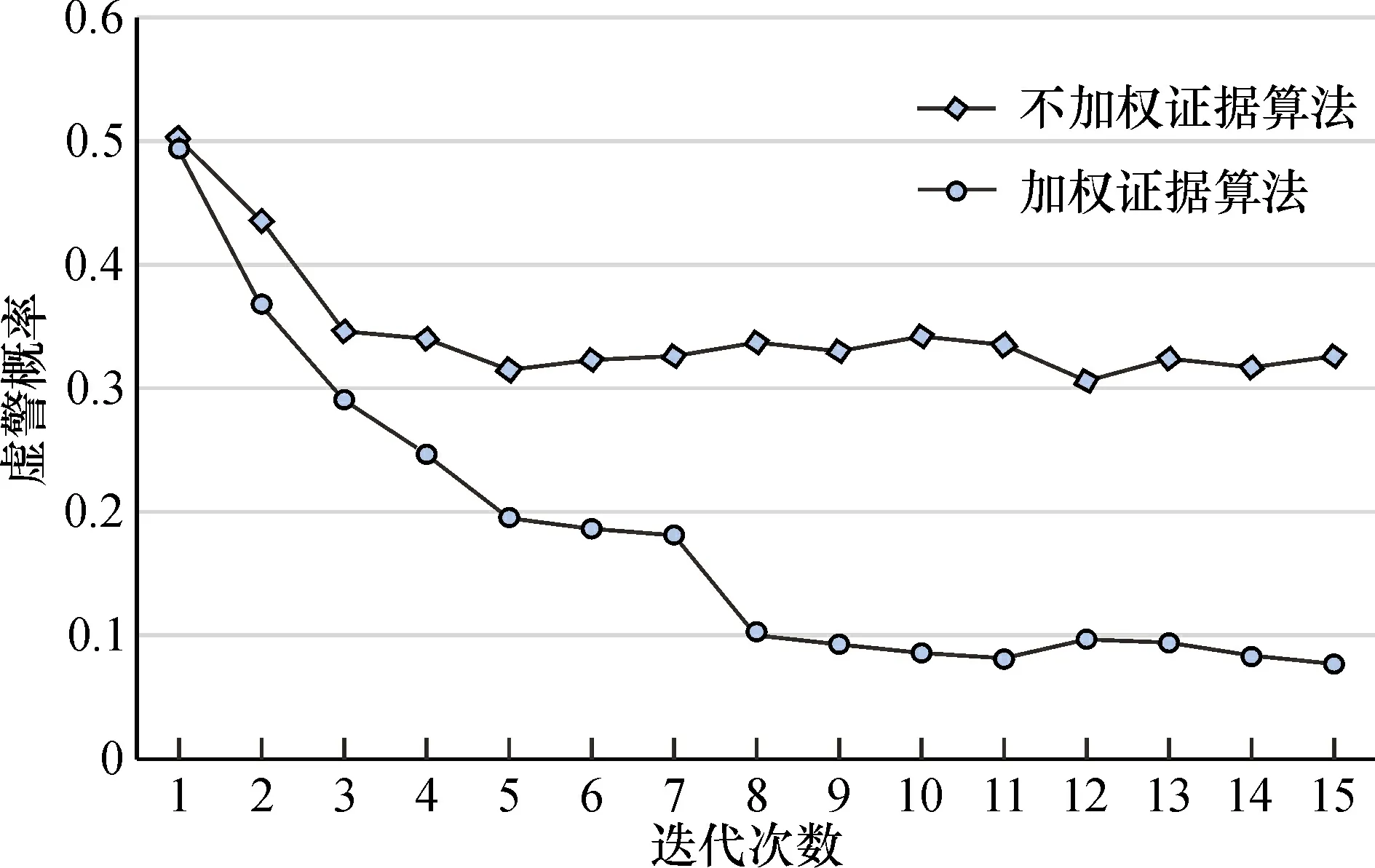
图5 算法的虚警概率Fig.5 False alarm efficiency of the algorithm

5 结束语

本文为解决海量数据节点产生和传输中的不确定性,提出在物联网节点加权的基础上用D-S证据理论对数据进行融合,并且设定目标识别的决策规则。在NS2的基础上进行物联网数据融合的仿真实验。利用基于节点权重的D-S证据理论对数据进行融合,根据节点权重大小以及节点间产生冲突概率的情况,对节点的权重进行调整,并按照D-S证据理论公式进行融合。通过NS2仿真软件进行对比实验,模拟结果表示基于节点加权的D-S证据理论可将证据冲突性、节点性能大小等众多因素综合考虑,验证在数据融合方面的有效性,即使节点权重很大,只要发生多次冲突就减小权重,保证融合结果的正确性,同时可使用户在收到融合数据后最大程度贴近真实效果。