改进灰狼算法优化SVM的大坝变形预测
2019-10-28朱军桃
朱军桃,程 胜,邢 尹
(桂林理工大学 a.测绘地理信息学院;b.广西空间信息与测绘重点实验室,广西 桂林 541006)
大坝变形常受温度、水位等诸多具备随机性和非线性因子的影响,使得传统的预测方法难以表达变形量与影响因素之间的复杂关系,预测效果常不令人满意[1]。目前,常用的监测模型有支持向量机(SVM)、人工神经网络[2]、时间序列模型、统计模型等,其中SVM模型适用于解决小样本、高维数、非线性的问题,具有良好的泛化能力[3],在大坝安全检测建模中得到了较多的应用。SVM是机器学习领域的一个热点算法,但回归性能受其内部参数影响很大,为此,许多研究者提出将粒子群算法[4](PSO)、 布谷鸟搜索算法[5](CS)、差分进化算法[6](DE)等运用于SVM的参数优化上, 并取得了良好的应用效果。 灰狼算法(GWO)是一种新型元启发式算法[7],且具备良好的稳定性和快速收敛性,但该算法在参数寻优过程中易陷入局部最优,进而影响SVM模型的预测性能。
鉴于此,本文提出引入非线性收敛因子和采用动态权重策略来改进灰狼算法(IGWO),并对SVM参数进行深度寻优。利用优化的参数建立SVM预测模型,并与PSO-SVM、CS-SVM、DE-SVM和GWO-SVM预测模型进行比较,本文提出的IGWO-SVM模型体现出了优越性,能够提高大坝预测精度。
1 支持向量机算法
用线性回归函数f(x)=w·x+b拟合数据{xi,yi},i=1,2,…,n,xi∈Rd,yi∈R的问题,根据SVM理论,若采用线性ε不敏感损失函数:
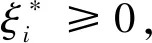
(1)
下,最小化目标函数
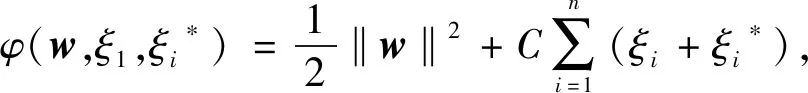
(2)
其中, 常数C>0控制对超出误差ε的样本的惩罚程度,采用优化方法可以得到其对偶问题,即在约束条件
(3)
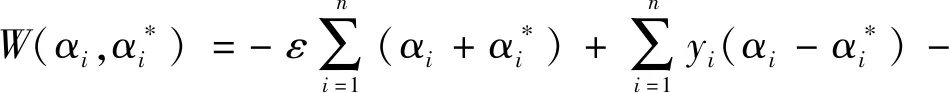
(4)
从而得到回归模型
(5)
其中,αi、αi*不为0, 对应的样本就是支持向量。 如果用核函数K(xi,xj)替代式(4)、(5)中的内积运算就可以确定非线性拟合函数
(6)
式(5)、(6)中的b*为取在边界上的一点,由此可确定;本文K(xi,xj)选用高斯径向基核函数(RBF),其表达式为K(xi,xj)=exp{-g‖xi-xj‖2},g为RBF核参数。
2 基本灰狼算法(GWO)
灰狼是一种食肉性动物,多以群居为主,群体内有着严格的社会等级管理制度,可形象描述为金字塔等级制,如图1所示。金字塔顶层为种群中的头狼,称为α,是狼群的主要管理者。金字塔第2层狼称为β,是α的协助者,当α出现空缺时,β将替补成为α,β在狼群中(除α外)对其他成员具有支配权,同时还起着协调反馈的作用。金字塔第3层狼称为δ,δ听从α及β的指令,可以指挥其他底层个体,年老的α及β也将降级为δ级别。金字塔最底层狼称为ω,主要负责种群内部关系的平衡。
在GWO算法中,由α、β、δ执行追捕行为,ω进行猎物跟踪围剿,对应于连续函数优化时,将当前种群中具有最优适应度值的个体记为α,排名第2及第3的个体分别记为β和δ,剩余个体记为ω,猎物的位置对应于优化问题的全局最优解,下面给出算法中的3个定义[8]。

图1 灰狼种群等级金字塔示意图Fig.1 Schematic diagram of the grey wolf population level pyramid
定义1灰狼与猎物之间的距离[7],在捕食过程中,灰狼首先需要对猎物进行包围,对应在GWO算法中,需要确定个体与猎物之间的距离
D=|EXp-X(t)|;
(7)
E=2r1,
(8)
其中,Xp表示猎物的位置;X(t)表示在t代时灰狼个体的位置;常数E为摆动因子;r1为[0,1]的随机数。
定义2灰狼位置更新[6]:
X(t+1)=Xp-AD;
(9)
A=2ar2-a,
(10)
其中,A为系数因子;r2为[0,1]的随机数;a随着迭代次数增加从2线性递减到0, 计算公式为

(11)
其中,Tmax是最大迭代次数。
定义3猎物位置定位[7],当灰狼判断出猎物所在位置时,将由头狼α带领β、δ发动追捕行为。 在狼群中,α、β、δ三者最靠近猎物,可以利用这三者的位置来判断猎物所在方位[8]。
狼群中个体跟踪猎物方位的数学描述如下:
Dα=|E1Xα(t)-X(t)|;
(12)
Dβ=|E2Xβ(t)-X(t)|;
(13)
Dδ=|E3Xδ(t)-X(t)|;
(14)
X1=Xα-A1Dα;
(15)
X2=Xβ-A2Dβ;
(16)
X3=Xδ-A3Dδ;
(17)
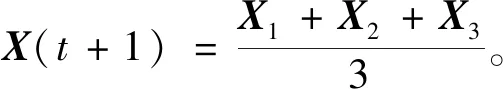
(18)
由式(12)~(17)计算出群内个体与α、β、δ的距离,然后由式(18)即可综合判断出个体向猎物移动的方向。基本GWO算法的具体步骤见文献[7]。
3 改进灰狼算法
3.1 引入非线性收敛因子
由于灰狼算法的收敛因子a是随着迭代次数线性从2递减到0,但算法在不断收敛过程中并不是线性的,收敛因子a线性递减策略不能完全体现出实际的优化搜索过程[9]。因此,本文提出一种新的非线性收敛方式[10]
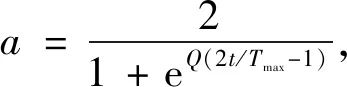
(19)
其中, e是自然对数的底数;t是当前迭代次数;Tmax是最大迭代次数;Q=9.903 438。 收敛因子a随进化代数非线性递减过程, 如图2所示。 可知, 收敛因子a随着迭代次数从2非线性递减到0。 进化初期, 收敛因子a平稳降低, 实现算法寻优的平稳过渡; 进化中期, 收敛因子a的衰减程度提高, 算法快速寻找全局最优解; 进化后期, 收敛因子a的衰减程度逐渐减低, 保证算法精确寻优, 并最终收敛。

图2 收敛因子a对比Fig.2 Comparison of convergence factors a
3.2 采用动态权重策略
由于灰狼算法的狼α不一定是全局最优点,这时在不断迭代过程中,随着狼ω不断地向着狼α、β和δ逼近,容易陷入局部最优[11]。通过评估狼α、β和δ所处位置优劣,引入动态比例权重,进一步调整灰狼位置,并最终精确捕食猎物。动态权重比例计算公式为
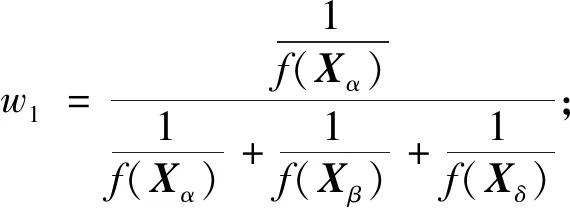
(20)
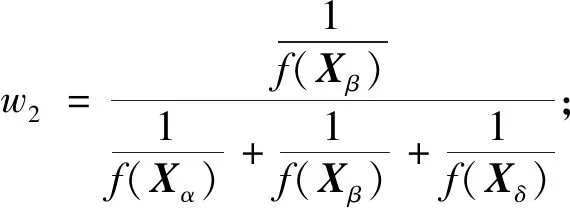
(21)

(22)
最终的迭代方式为
X(t+1)=

(23)
其中:适应度函数f(X)=1/MSE,MSE表示均方误差。
3.3 IGWO-SVM算法步骤
① 给定实验数据,确定训练样本和测试样本,并进行归一化操作:
(24)
式中,x为输入数据;y为归一化后数据。
② 给定种群规模N,最大迭代次数Tmax,以及优化参数取值范围。
③ 随机产生初始种群Xi为
Xi=r0(ub-lb)+lb,
(25)
其中:lb和ub分别为参数取值的下界和上界;r0为[0,1]间的随机数;i=1, 2, …,N。
④ 计算每一头灰狼位置的适应度值, 并进行升序排列, 排名前3位的灰狼位置分别记为Xα、Xβ和Xδ。
⑤ 按照式(19)更新a, 并根据式(12)~(14)计算出群体内个体与α、β、δ的距离; 然后由式(15)~(17)和式(20)~(23)判断个体向猎物移动的方向,得到新的个体位置X(t+1), 即得到新的SVM参数值。
⑥ 若达到最大迭代次数, 则终止迭代, 输出最优参数C和g; 否则返回④。
⑦ 采用优化的参数C和g建立SVM预测模型。
4 实验结果与分析
选取丰满大坝某一测段1985年1月4日—1988年7月13日的200期多源监测数据,如图3所示。

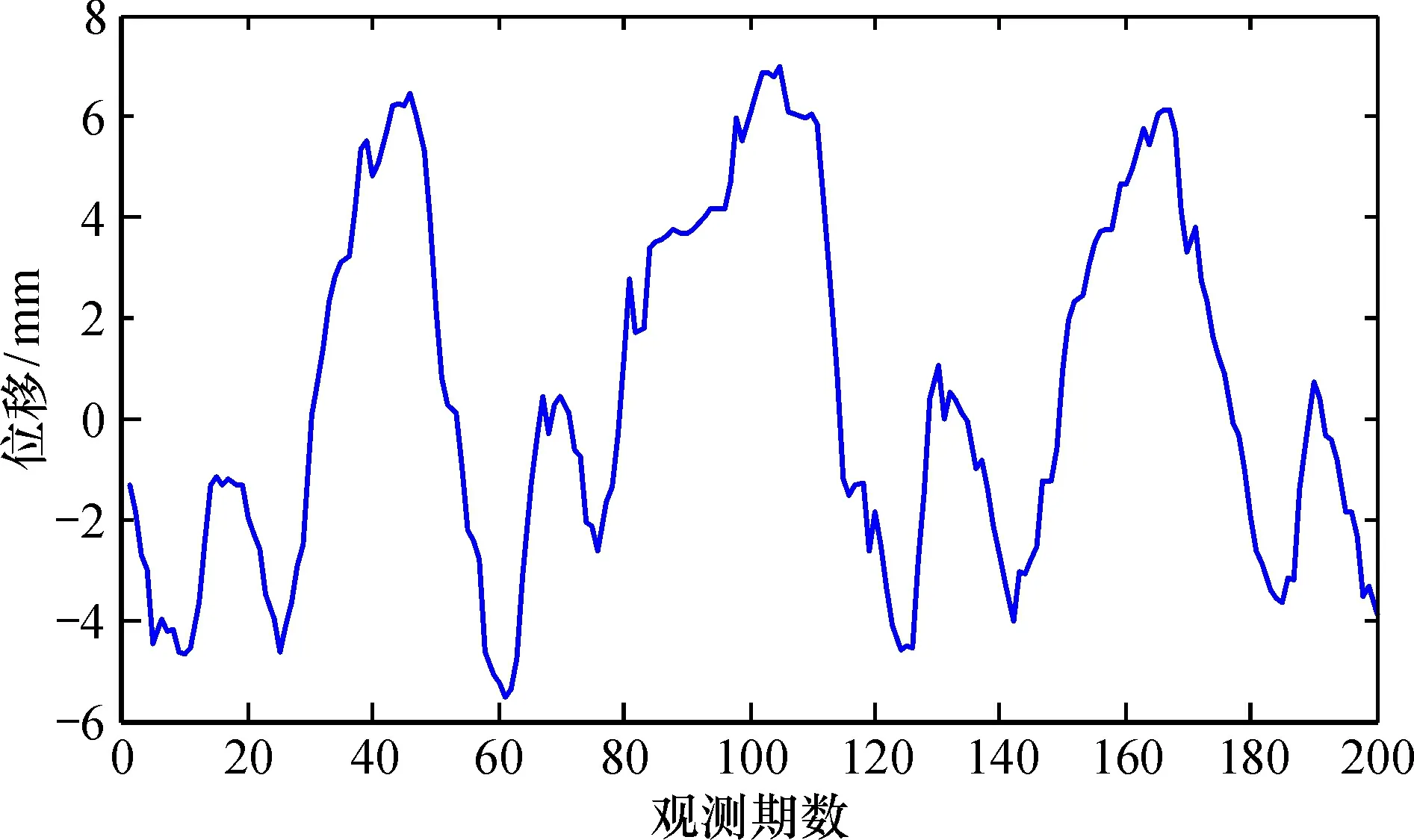
图3 大坝水平位移序列Fig.3 Sequence of the horizontal displacement of the dam
为了评价模型预测效果, 选用均方误差(MSE)、 平均相对误差(MRE)、 误差标准差(SDE)、 确定性系数(R2)这4个评价指标,它们分别为
(26)
(27)
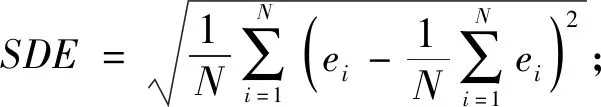
(28)
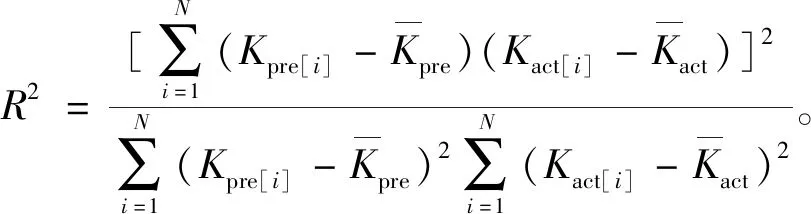
(29)
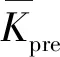
为了说明本文所建立的预测模型优越性,分别采用布谷鸟搜索算法(CS)、差分进化算法(DE)、粒子群算法(PSO)、灰狼算法(GWO)和改进灰狼算法(IGWO)对SVM模型进行优化。所有优化算法的种群规模都设置为20,最大迭代次数设置为100。此参数设置均保持了各算法具备充足的种群规模和迭代数以达到收敛状态。其中,CS中鸟蛋被宿主发现概率为0.25;DE交叉概率因子为0.8;PSO加速因子c1=c2=1.5; SVM参数寻优范围设置为C∈[0.01,100],g∈[0.01,100]。
5种算法优化的SVM参数结果见表1。采用其中的参数C和g作为SVM参数,对训练集进行学习,建立相应的CS-SVM、DE-SVM、PSO-SVM、GWO-SVM及IGWO-SVM的大坝预测模型。
图4给出了IGWO-SVM模型大坝位移变形预测值与原始观测值的比较图。IGWO-SVM模型大坝位移变形预测值与原始观测值之间的残差,如图5所示。进一步给出另外4种模型预测结果,统计结果见表2。从图4、5和表2可以看出,IGWO-SVM模型预测曲线与实际观测曲线贴合效果很好, 其R2值达到了0.955 6, 均高于另外4种预测模型;IGWO-SVM模型的MRE和MSE值均最小,说明IGWO-SVM模型具有更高的预测精度;IGWO-SVM模型的SDE值也均小于另外的4种模型,说明IGWO-SVM模型的预测结果更加稳定。另外,由表2还可以看出,IGWO-SVM模型具有较短的优化CPU时间, 进一步说明IGWO-SVM模型对SVM参数优化的性能更优越。综上,证明了IGWO能够提升GWO的优化性能,进而建立预测性能优越的SVM回归模型。
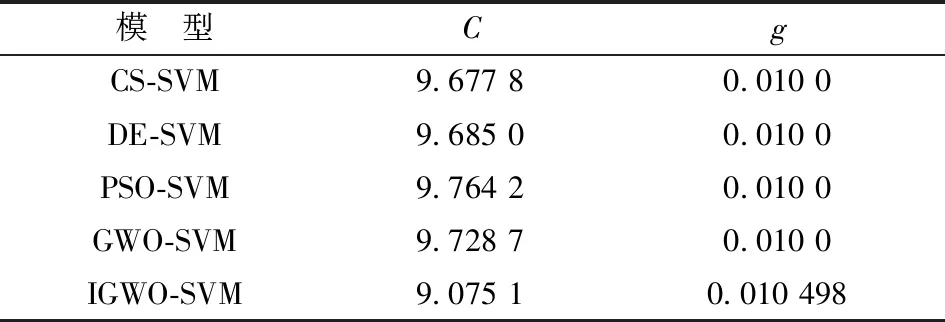
表1 5种算法优化SVM参数结果

图4 IGWO-SVM模型大坝水平位移预测结果Fig.4 Result of the horizontal displacement of dam predicted by IGWO-SVM model
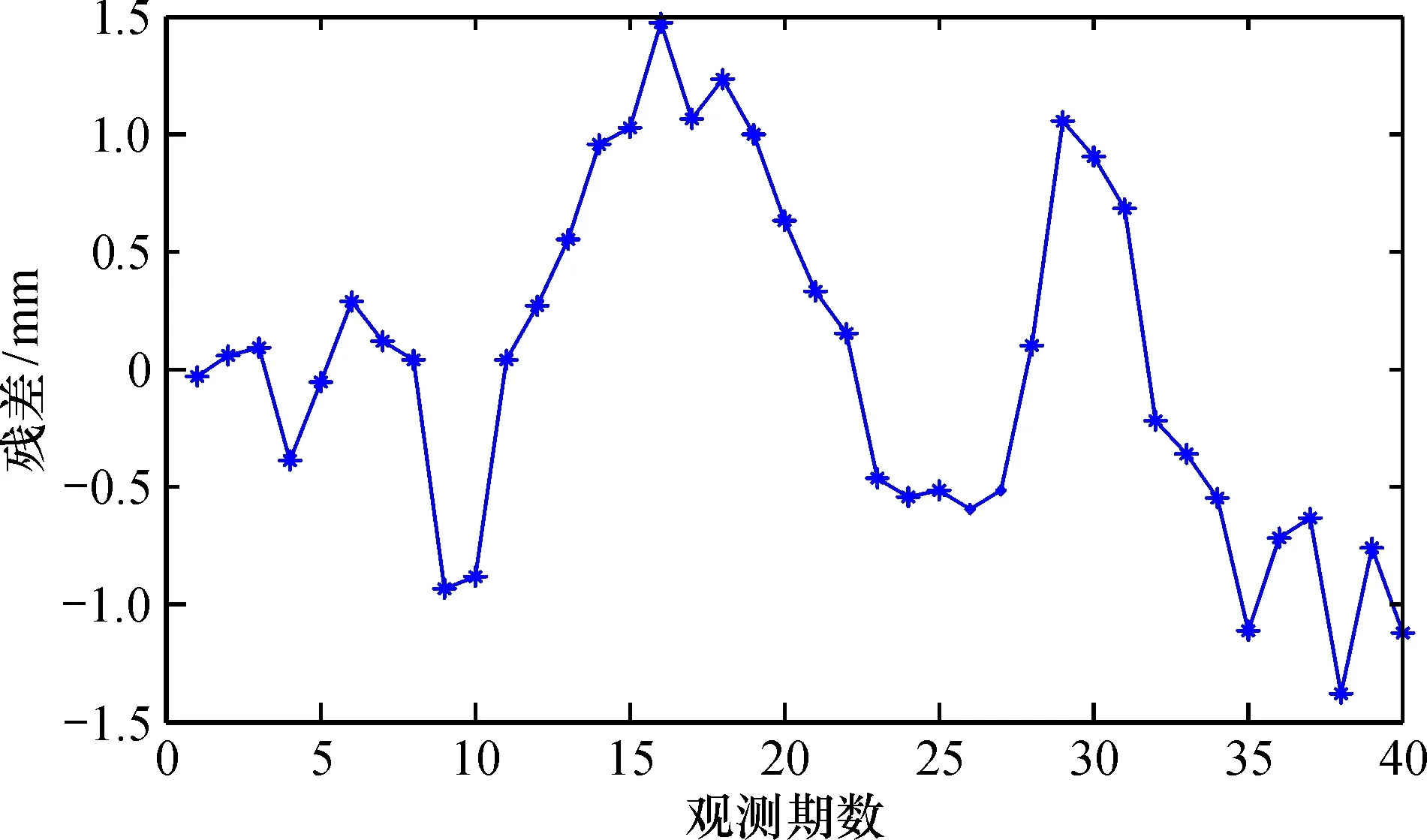
图5 IGWO-SVM大坝水平预测残差Fig.5 Residual error of the horizontal direction of the dam predicted by IGWO-SVM
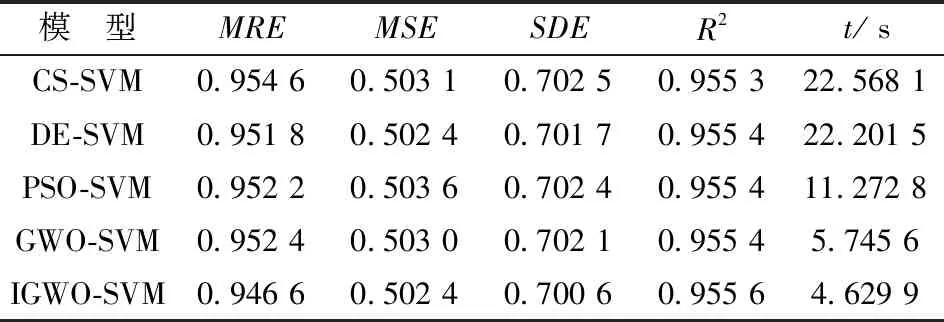
模 型MREMSESDER2t/sCS-SVM0.95460.50310.70250.955322.5681DE-SVM0.95180.50240.70170.955422.2015PSO-SVM0.95220.50360.70240.955411.2728GWO-SVM0.95240.50300.70210.95545.7456IGWO-SVM0.94660.50240.70060.95564.6299
5 结 论
本文提出了一种基于改进灰狼算法优化支持向量机的预测模型。在灰狼算法的基本原理上,引入非线性收敛因子和采用动态加权策略来进一步提升基本灰狼算法优化支持向量机参数的性能,并根据最优参数建立大坝预测模型。实验结果表明,相对于参比模型,IGWO-SVM能更加准确地刻画大坝复杂变化趋势,有效提高预测精度,为大坝预测提供了一种新的方法。
