二维耦合热弹性动力学问题的无网格自然邻接点Petrov-Galerkin法
2019-10-28李庆华陈莘莘
李庆华,陈莘莘
(华东交通大学 土木建筑学院,南昌 330013)
当结构受到温变,一般会产生热应力,并且热应力是物体破坏的一个重要因素[1-2]。对受热结构进行分析时,解耦方法可先由热传导方程求出温度分布,再由热弹性方程求解位移和应力。但是,解耦方法没有考虑结构变形对温度场的影响[3]。事实上,热弹性力学中最基本的问题就是耦合热弹性问题。在耦合热弹性问题中,温度和变形会相互影响,温度场和应变场的耦合项必须体现在热传导方程中。为了求解温度、位移和应力,必须联立求解热传导方程和热弹性运动方程。相对于非耦合热弹性问题,耦合热弹性问题求解更困难。
热应力问题的数值方法主要基于发展较为成熟的有限元法[4-5]和边界元法[6-8]。近年来,部分学者尝试采用无网格法[9-12]求解热应力问题。无网格法不仅能够避免网格生成的复杂过程,而且在节点分布不规则时,损失的计算精度较小,从而日益得到重视[13-14]。近十多年来发展起来的无网格法―无网格自然邻接点Petrov-Galerkin法[15-16]不仅允许加权函数和试函数取自不同的函数空间[17],而且克服了本质边界条件不易施加的困难。此方法中,所有的积分都在中心为所考虑点的多边形子域上进行,而且多边形子域的构造十分方便。目前,无网格自然邻接点Petrov-Galerkin法在很多领域都得到广泛应用[18-20]。本文采用自然邻接点插值对温度和位移分别插值,与局部加权余量法结合,提出了适用于耦合热弹性动力学问题的无网格自然邻接点Petrov-Galerkin法。最后,通过数值算例验证了本文方法应用于耦合热弹性动力学问题分析的有效性和合理性。
1 自然邻接点插值
在求解域内给定M个离散节点,其集合为N={x1,x2,…,xM}。对任一节点xI,其一阶Voronoi结构可定义为
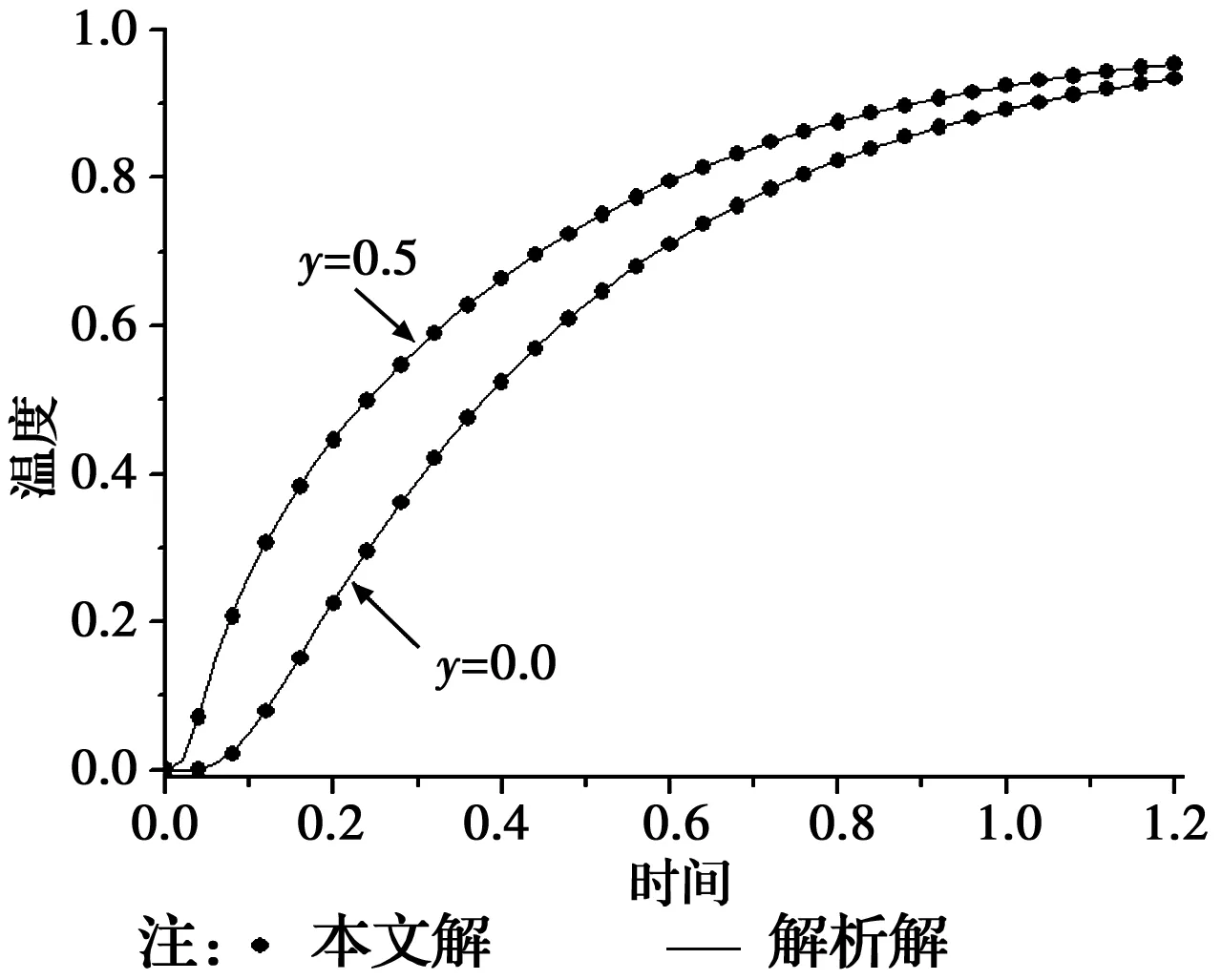
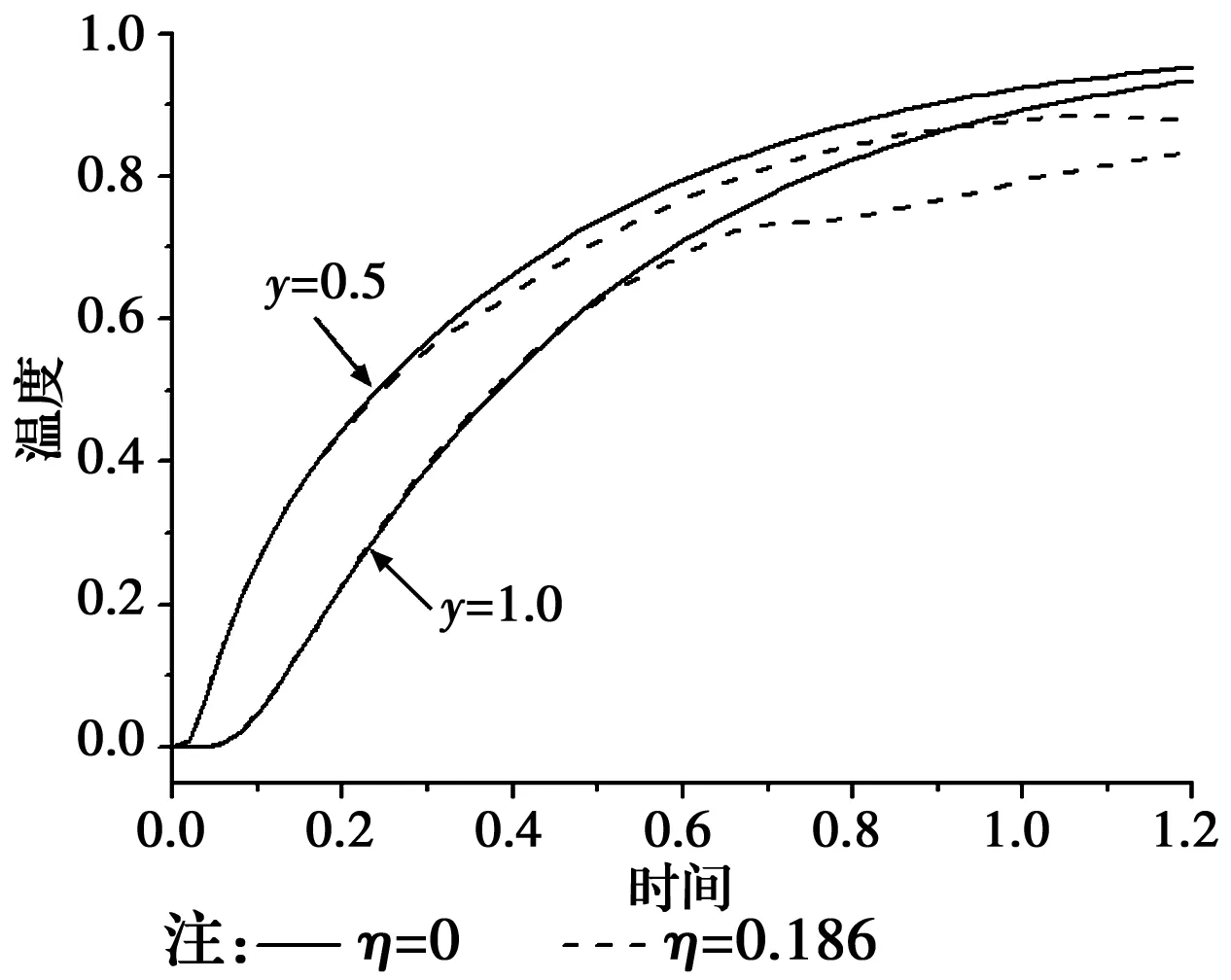
TI={x∈R2:d(x,xI) (1) 式中:d(x,xI)表示点x与节点xI之间的距离。 为计算Sibson插值形函数,需进一歩定义二阶Voronoi结构。 TIJ={x∈R2:d(x,xI) d(x,xK),∀J≠I≠K} (2) 图1所示为点x的一阶和二阶Voronoi结构。根据Sibson插值的定义[15],点x的插值函数为 φI(x)=AI(x)/A(x) (3) 式中:AI(x)为点x的二阶Voronoi结构TxI的面积;A(x)为点x的一阶Voronoi结构Tx的面积。 图1 点x的一次和二次Voronoi结构Fig.1 First-order and second-order Voronoi cells about 定义了各节点的插值函数后,点x的温度函数类似于有限元法可写为 (4) 式中:θI(I=1,2,L,n)是点x周围自然邻接点的节点温度。 设线性耦合热弹性动力学问题的区域为Ω,Γ为Ω的边界。热弹性力学的应力、位移与温度之间的关系为[1] σij=2μεij+λεkkδij-βθδij (5) 式中:σij为应力;εij为应变,λ和μ为拉梅常数;β为热应力系数;θ为温度变化值。小变形情况下,应变εij与位移ui的几何关系为 εij=(ui,j+uj,i)/2 (6) 在经典的热弹性理论中,运动方程和热传导方程可表示为[1] (7) (8) (9) (10) (11) (12) θ(x,0)=θ0,x∈Ω (13) u(x,0)=u0,x∈Ω (14) v(x,0)=v0,x∈Ω (15) 式中:θ0为初始温度;u0和v0分别为初始位移和初始速度。 (16) (17) 式中:vI为加权函数。对式(16)左边积分的第1项进行分部积分并利用散度定理后,可得 (18) (19) 图2 局部多边形子域Fig.2 The local polygonal 以此类推,式(17)可变为 (20) 由于只对空间域进行离散,求解域Ω内的位移u(x,t)和温度θ(x,t)可由式(4)表示为 (21) 将式(21)代入式(19)和式(20),可得耦合热弹性动力学问题的离散控制方程为 (22) (23) 式中: (24) (25) (26) (27) (28) (29) (30) (31) 式中: (32) (33) (34) (35) (36) (37) (38) 对于平面应变问题,需把E换成E/(1-v2),v换成v/(1-v),α换成(1+v)α。式(22)和式(23)可合并为 (39) 式(39)即为施加边界条件后的系统耦合微分方程组,可采用Newmark方法[21]进行求解。 为了验证所提方法的有效性,考虑如图3所示的单位面积方板,该问题为平面应变状态下的一个经典算例。初始时刻板的温度和位移均为0,板上边受到突加的热载荷,另外3边均绝热,且无法向位移。弹性模量E=1,泊松比v=0.3,导热系数k=1,密度ρ=1,比热容c=1,热膨胀系数α=0.02。计算中,采用15×15个节点将方板离散,时间步长取为2.0×10-3。 图3 突加热载荷的方板Fig.3 A suddenly heated unit square 当不考虑惯性项和耦合项时,此问题属于准静态热弹性力学问题。图4和图5分别给出了方板y轴上不同坐标处的温度和竖向位移变化情况。从图4和图5可以看出,本文数值解与解析解[22]吻合得很好。 图4 温度随时间的变化Fig.4 Temporal variation of the 图5 竖向位移随时间的变化Fig.5 Temporal variation of the vertical 当考虑惯性项时,为了便于对耦合和非耦合情况下的计算结果进行比较,引入如下修正的耦合系数[12] (40) 式中:耦合系数η的取值范围一般为0.01~0.2。相关温度取为θ0=100,则对应的耦合系数为η=0.186。图6和图7分别为y轴上不同坐标处耦合项对温度和位移的影响。显然,耦合项对温度的影响很大,但对位移的影响可忽略不计。 图6 耦合效应对温度的影响Fig.6 Coupling effects on the 图7 耦合效应对竖向位移的影响Fig.7 Coupling effects on the vertical displacement 无网格自然邻接点Petrov-Galerkin法是一种简单适用,且效率和精度均十分优良的无网格分析方法。在采用自然邻接点插值对位移和温度分别插值的基础上,将FEM三角形线性单元的形函数作为加权函数,采用加权余量法详细推导了二维耦合热弹性动力学问题的无网格自然邻接点Petrov-Galerkin法计算公式。数值算例表明,所提的二维耦合热弹性动力学问题求解方法可行。
2 控制方程的弱形式及其离散化

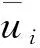



3 数值算例



4 结论
