沉降自动化监测预警系统在运营铁路中的应用与研究

王 杨

(1. 中国铁路郑州局集团有限公司科学技术研究所,河南郑州 454000;2. 郑州铁路科技发展有限公司,河南郑州 454000)

目前,人工测量和内业分析相结合的监测方式依 然是我国铁路大型基础设施变形及沉降监测的主流方式。 传统测量方式需要人工设站,测量时段和频率受限,后期还需要对数据进行二次处理,导致监测报告的输出严重滞后,已经不能满足铁路运营维护效率的需求。

对于需要上道测量的工程项目,人工测量必须在铁路“天窗”内进行,为保证工期,往往需要投入大量的人力和财力。 因此,针对铁路监测的特殊性,研发一套保证测量精度、提高测量效率的铁路自动化监测系统十分必要。

李德桥等[12]提出了一种基于磁致式静力水准仪的沉降远程监控系统,其实验室条件下的线性度、稳定性、沉降测试精度满足土木工程沉降的监测要求。 孙泽信[3]等认为列车运行对基于静力水准仪的监测结果有较大影响。 禚一[4]等研发了高速铁路沉降自动化监测系统,并成功应用于京津城际铁路,但受列车运行和外界温度影响较大。

为了能够减少震动、温度和气压对静力水准系统产生的影响,研发了“沉降自动化监测预警系统”。 在直接数据采集的基础上,增加了卡尔曼滤波(过滤震动产生的瞬时变化),并通过系统数据分析生成补偿系数,修正温度和气压造成的影响。

1 自动化监测预警系统简介

1.1 系统组成

铁路沉降监测预警系统由传感器子系统、数据采集子系统、数据传输子系统和控制中心4 部分组成,各部分功能如下。

(1)传感器子系统:由布设在监测区域现场的静力水准仪组成,用于实时获取沉降数据。

(2)数据采集子系统:由采集单元、供电单元、防雷模块等组成,用于采集传感器数据并接受指令。

(3)数据传输子系统:采用GPRS 网络,实现与监控中心的数据通信。

(4) 控制中心:由监控服务器、监控终端及相关软件组成。

1.2 静力水准仪

静力水准仪结构简单、精度高,采用水路连接,无须通视,适应铁路周边环境,易于实现自动化监测。 精力水准监测的基本原理就是连通器原理,即通过水位变化达到测量的目的。 其理论精度最高可达1 μm,一般可达0.1 mm。

如图1 所示,假定左侧的静力水准为基准点,右侧的为测量点。 从左到右依次显示了液面随着位置的变化而变化。

假设有n 个观测点,且各观测点已联通,其初始状态各个观测点的高程记为Y01…Y0i…Y0j…Y0n,各个观测点的液面高度依次为h01…h0i…h0j…h0n。

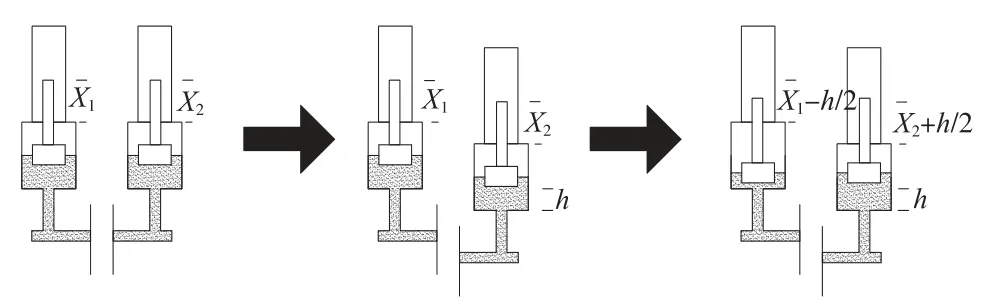
图1 静力水准测试原理

初始状态显然满足

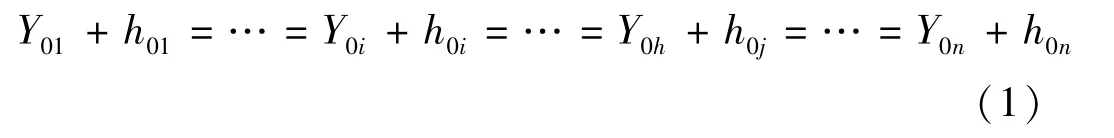
当不均匀沉降发生k 次后,由于沉降引起的各观测点变化量为Δhk1…Δhki…Δhkj…Δhkn,此时各观测点对应的液面高度为hk1…hki…hkj…hkn。

各观测点静力水准仪保持联通,各液面保持水平,故有

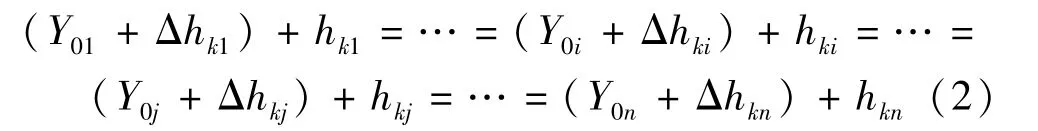
观测点j 相对于基准点的沉降量为

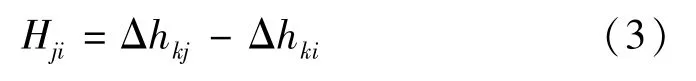
由式(1)可知

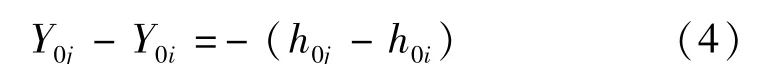
由式(2)可知

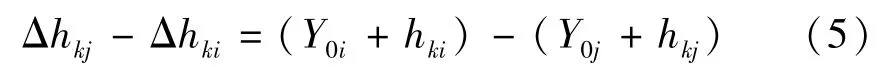
将式(4)代入式(5),可以得到

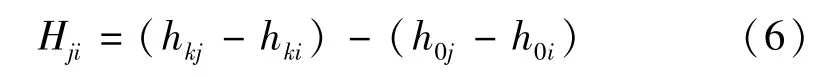
由式(6)可知,各观测点沉降值可以通过不同时刻与基准点的液面高度计算得出。

2 精度试验

取3 支静力水准仪,将其中1 支固定在千分尺升降平台上(千分尺升降平台可自由升降,分辨率可达0.01 mm);其余2 支分别固定在稳定平面上(作为基准点和对比点)。 调节升降平台,将测量结果与升降真值对比。

该试验共分2 次,标定架分别下移0.50 mm,5.50 mm。 测量结果如图2。

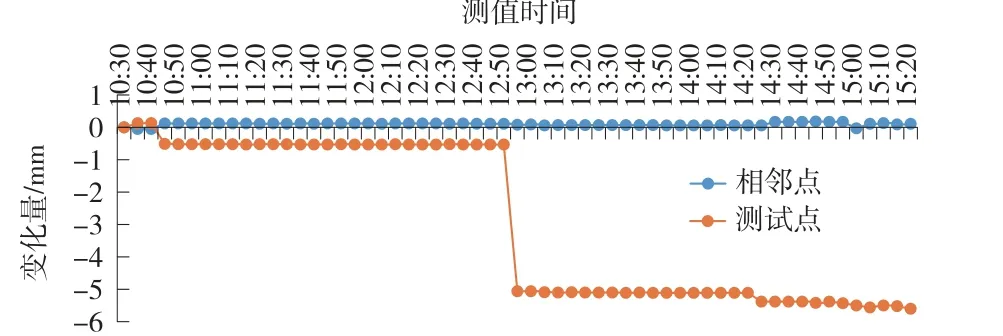
图2 精度测量变形曲线

假设标定架的移动变形量为真值,对静力水准仪的测量变形量与真值进行比较,移动0.5 mm 时,较差约为0.03 mm;移动5.5 mm 时,较差最大为0.1 mm。通过试验可以看出,静力水准仪能够精确地监测位移的变化,且具有较高的精度。

由图2 可以看出,当位移发生时,静力水准仪能够快速识别,但达到精确测量需要一定的时间。 当移动0.5 mm 时,约花费15 min 识别到位移信息,且得到准确值;当移动5.5 mm 时,静力水准仪能够立刻识别到变化,但液面回归准确值大约需要2 h;在对静力水准仪进行调整时,相邻点静力水准仪会受到一定影响,液面波动约为0.1 mm。

进一步计算出每次调整并稳定后的最后5 次读数与真值(调整值)之间的中误差,见表1。

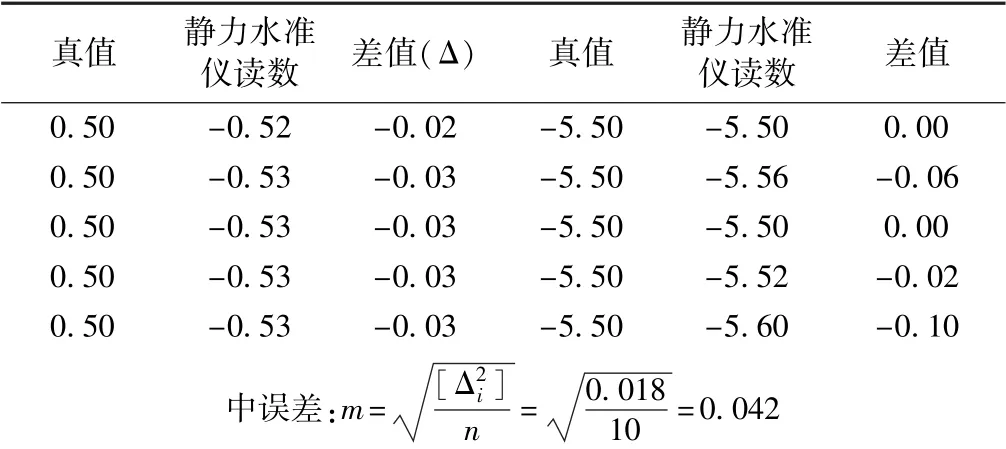
表1 静力水准仪精度测试结果中误差 mm

在《工程测量规范》和《铁路工程测量规范》关于变形监测的等级划分和精度要求中,变形观测点的高程中误差:一等为0.30 mm,二等为0.50 mm。 因此,在实验室条件下,该套系统可以满足一等水准测量的技术要求。

3 核心算法

3.1 自适应卡尔曼滤波筛选

传感器安装在铁路附近,在列车通过时不可避免地会受到震动影响,从而影响精度,造成误报。 为消除震动影响和剔除系统原因产生的异常值,采用自适用卡尔曼滤波对数据进行筛选,剔除列车震动造成的影响。

卡尔曼滤波的基本原理是采用相关因子及其变率作为状态因子,通过在初始时刻的观测量来构建动态平差模型,以获得初始状态值,并通过状态转移矩阵及观测方程构建卡尔曼滤波模型,其核心是此刻与下一刻状态之间的转换关系[7]。

卡尔曼滤波的基本方程式为

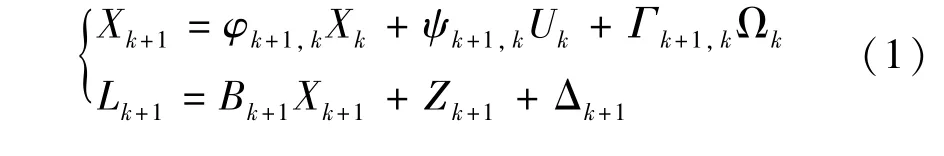
式中:Zk+1=Gk+1Uk+1,Gk+1为控制向量系数阵,Xk、Xk+1为状态向量在tk、tk+1的滤波值,Uk、Uk+1为控制向量,Ωk为动态噪声向量,Δk+1为观测噪声向量,φk+1,k为状态向量系数阵,ψk+1,k为控制向量系数阵,Γk+1,k为动态噪声向量系数阵。

当没有确定性输入时,则状态方程和观测方程可简化为

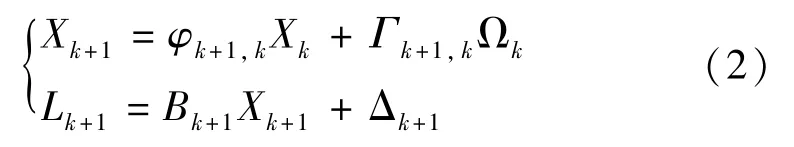
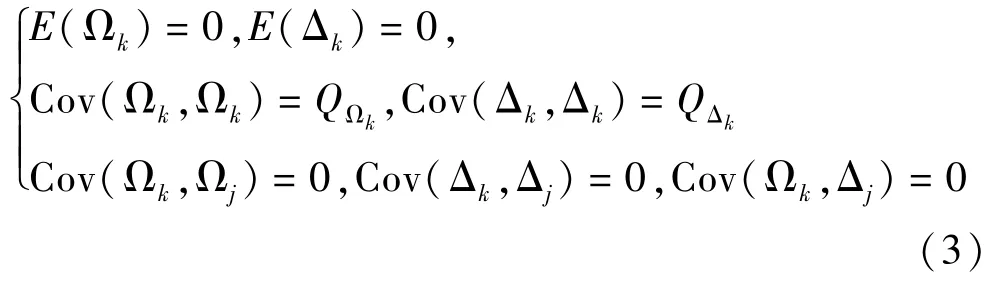
随机模型为

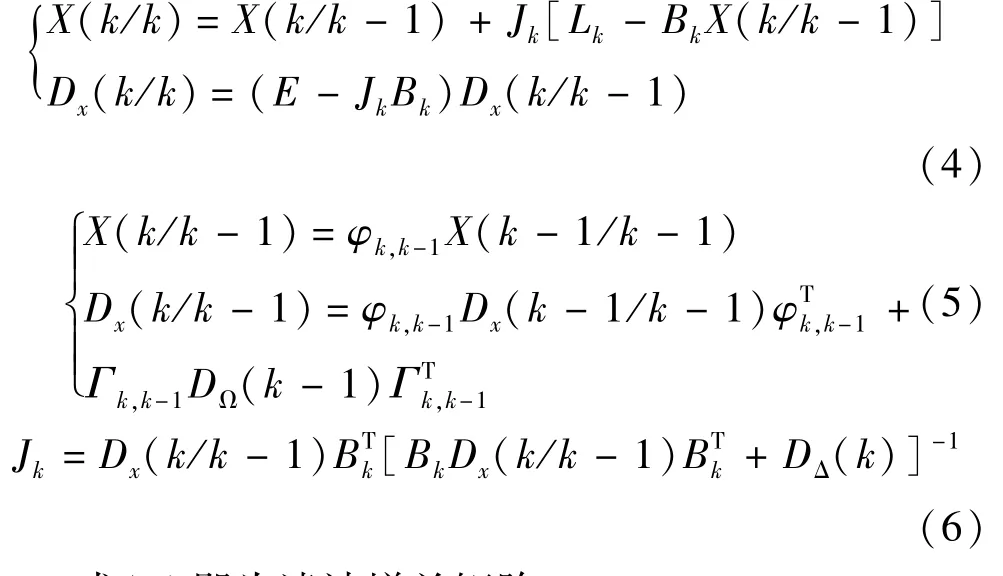
卡尔曼滤波方程为

式(6)即为滤波增益矩阵。

假定{Ωk}和{Δk}为正态序列,X0为正态向量,定义i 步预测残差为

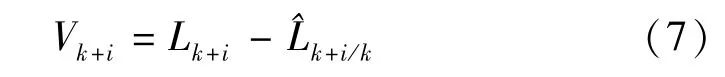
其中:Lk+i,^Lk+i/k为第k+i 期观测值及其最佳预测值,Vk+i为预测残渣。 而^Lk+i/k=Bk+iφk+i/kXk+Δk+i,则Vk+i的方差阵为

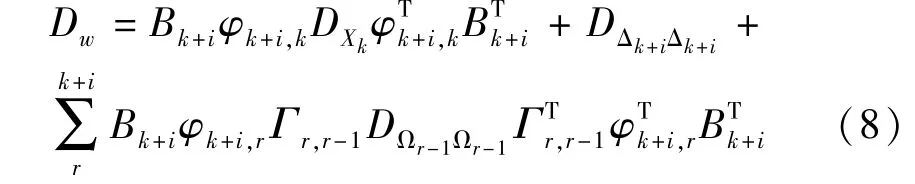
另记Bk+iφk+i,rΓr,r-1=A(k+i,r)= [a(k+i,r)hj]式中:r=1,…,N;k=1,…,n;上标k+i,r 表示与k+i,r 有关。 假定DΩr-1Ωr-1在tk+1,tk+2,…,tk+N上为常值对角阵,即

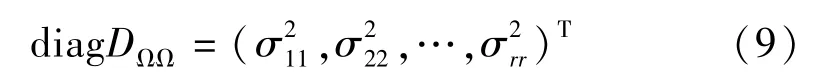
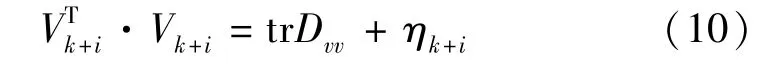
其中:ηk+i为零均值随机变量,i=1,…,N,令

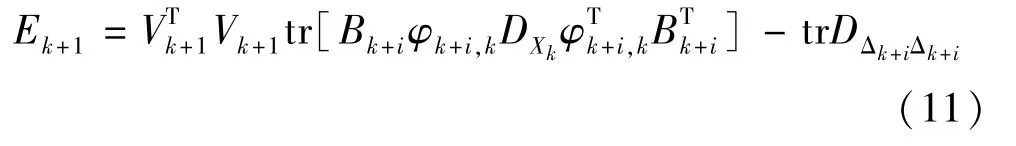
式(12)是diagDΩΩ的线性方程组。 当N≥r 时,有唯一解。 记diagDΩΩ的LS 估计为

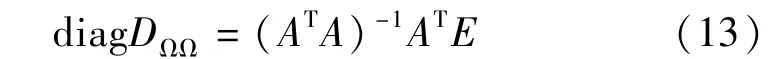
根据以上各式可求得任意长度时间段上的DΩΩ,并作为动态噪声协方差阵的实时估计。

3.2 数据建模生成补偿系数

虽然部分静力水准仪自身已具备温度补偿功能,但其补偿值仅限于仪器自身,而静力水准仪系统是一个完整的水路系统,储液罐、水路管线等并不具有补偿功能。 因此,在不同的环境下受到温度、气压等外界环境的影响不尽相同,而且精度越高的静力水准仪往往越容易受到外界环境的影响,仅通过滤波无法过滤掉此类干扰因素。 因此,必须选择一个补偿系数对监测值进行修正,以此获得真实的影响值。

由前期采集的沉降监测数据,利用抛物线差值法拟合温度曲线,针对单独的点位生成独立的补偿系数。在生成补偿系数后,系统后台能够通过监测数据不断修正补偿系数,以适应外界环境的变化。 系统在通过12 ～24 h 的数据采集并生成第一组补偿系数后,即可进入正常工作状态。

4 监测实例

某防护涵穿越铁路路基,采用泥水平衡法施工。涵址处铁路路基填土高度约4.0 m,其中,上行线西侧路基边坡采用拱形骨架进行防护。

据地勘资料,涵址处地层主要为黏土及砂卵石,呈多层结构。 第一层为黏土,层厚5.5 m 左右,呈黄褐色、棕红色,硬塑状态,基本承载力为160 kPa;第二层为砂卵石,层厚6 m,灰褐色,卵砾石含量约占55%,粒径在1 ～10 cm 之间,级配良好,中密状态,基本承载力为400 kPa;涵底位于第二层。 场区地下水类型属第四系松散岩类孔隙潜水,勘探期间地下水埋深7.00 ～8.00 m,高程153.11 ～154.11 m。 沉井底高程为150.66 m,沉井封底需在水下进行。

该工程始发井距离路基坡脚约20 m,穿越铁路段管线为D820*10 mm 螺旋焊接钢管。 防护涵主体采用圆管防护涵,防护涵设计总长度为70 m,每节长2.0 m,共35 节。 防护涵主体采用壁厚0.2 m 的FB 型钢筋混凝土圆管,两端出入口处设置工作井与接收井,采用泥水平衡法顶进施工。 管道埋深为地面以下6.0 m,线路允许通过速度为100 km/h。

监测点点位布置如图3。

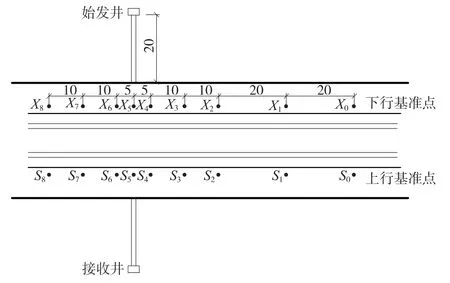
图3 监测点布置(单位:m)

为验证自动化监测数据的准确性,采用电子水准仪进行人工监测复核,监测点和基准点与自动化监测选点一致。

自6 月13 日开始自动化监测,每30 min/次;6 月26 日开始人工监测第1 次数据采集;6 月28 日2:00 左右开始顶进,顶进速度约1 m/h;6 月29 日6:00 人工监测未发现沉降(第2 期);6 月29 日12:00,下行线X5监测点(顶进中轴线上的监测点)沉降量为4.15 mm,超过预警值4 mm,系统通过短信预警,收到预警后立即向施工方反馈,此时盾构机已越过监测点,位于下行线路正下方;6 月29 日13:00,X5点变化量达到4.48 mm(人工监测第3 期),此时要求每日早晚各测量1 次;6 月30 日0:00,上行线S5(顶进中轴线上监测点)超过预警值4 mm,此时下行线X5监测点沉降量已超过11 mm,下行线X4和X6沉降量也超过预警值,且沉降量仍在持续增加;6 月30 日对线路高低进行测量(轨道变化量为5 mm)。 7 月1 日晚,顶进全部结束,开始注浆;7 月2 日凌晨起,沉降趋势开始放缓;7 月10 日沉降停止。

为更好对比该系统数据的准确性,将人工监测数据和自动化监测数据进行拟合分析。 其中,自动化监测系统每30 min 采集一次数据,每点每日数据量为672 个;人工监测为每日2 次,每点每日数据量为2个。 由于数据较多,仅展示X1和X5两处监测点拟合曲线。 为更严谨的对数据进行比对,提取出与人工监测时刻相同或接近的自动化监测数据进行比对(见图4)。

由图4 可知,两组数据高度吻合,变形观测点高程中误差仅为0.158 5 mm(如表2 所示),最大差值为1.39 mm,发生在X5处。 排除掉沉降影响区范围内各观测点(X4、X5、X6、S4、S5、S6)后,两组数据最大差值仅为0.31 mm。 从以上分析可以看出,各监测点静力水准监测数据与人工监测数据变化趋势和变化量高度相 似,吻合度高。

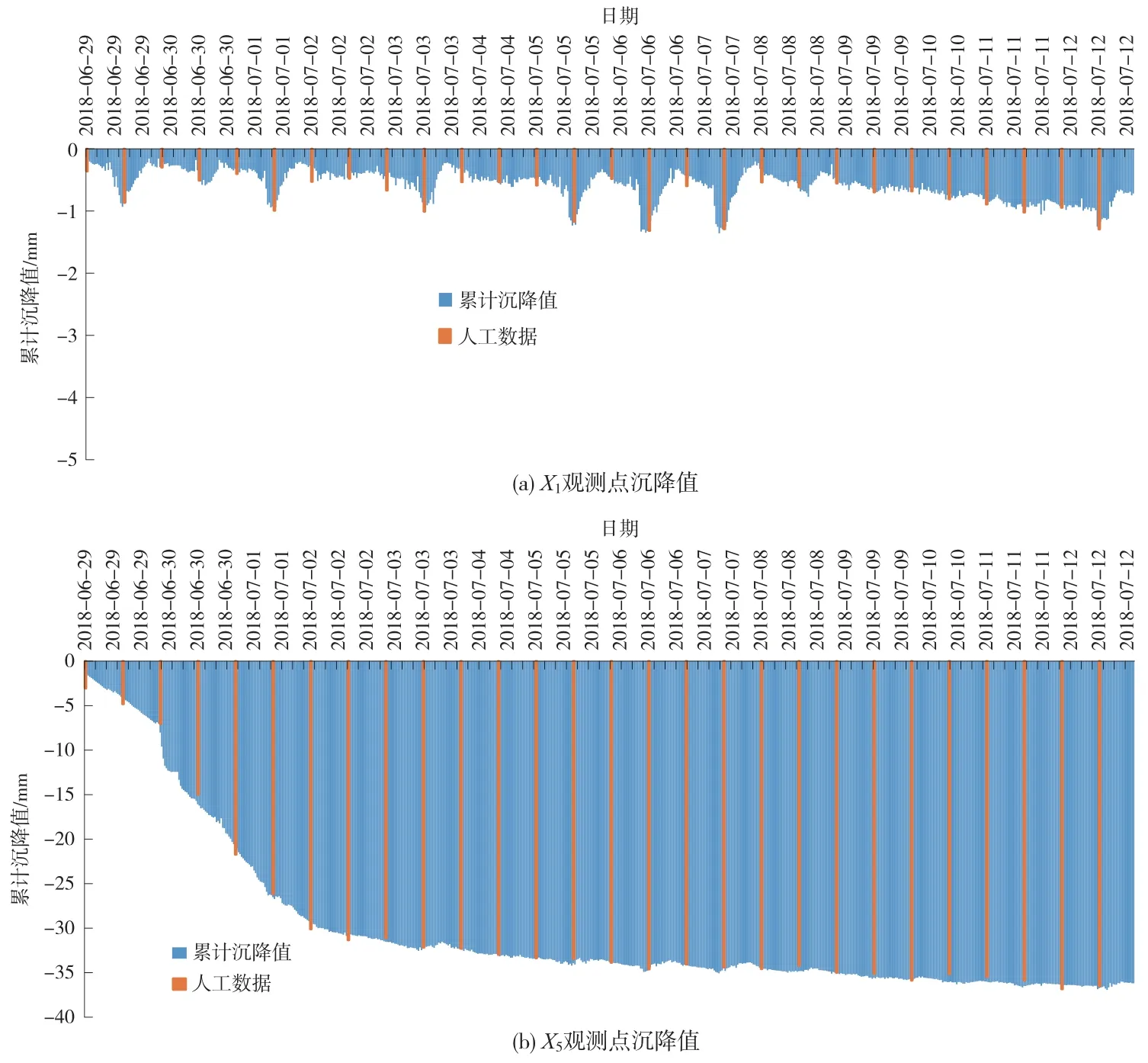
图4 监测点X1、X5 监测数据拟合

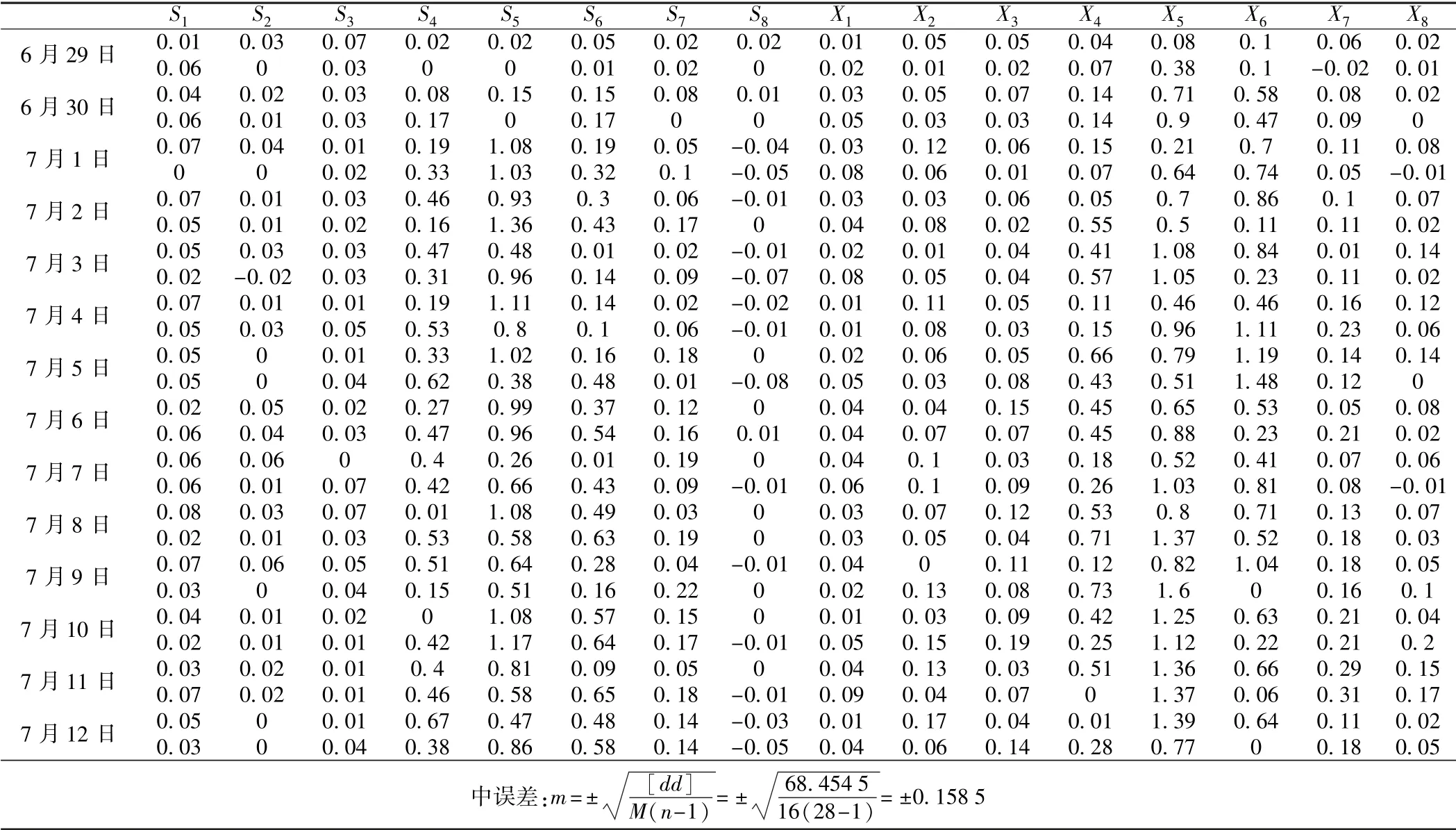
表2 静力水准仪精度测试结果中误差mm

5 结论

(1)位移在小范围内变化时,静力水准仪能够快速识别并达到真值;位移变化较大时,静力水准仪能够快速的发现变化,但得到准确值需要一定的时间。

(2)相较于人工监测,自动沉降监测系统可以做到实时监测并及时发出预警,极大地提高了监测的效率和可靠性。

(3)在滤波和温补系数的修正下,能够消除外界环境的影响,更加精准的对铁路桥、隧、路基进行监测。