基于三维激光扫描技术的既有铁路道岔岔心自动提取方法

张云鹏

(中铁第六勘察设计院集团有限公司,天津 300308)

道岔测量是铁路既有站场测量中的一项重要内容。 在站场平面图上,道岔的位置是由道岔中心的位置表示的。 道岔中心又称岔心,是指主线和侧线中心线的交点。 目前,铁路道岔岔心测量主要采用人工测量的方式,先通过现场丈量标定出岔心位置,然后使用全站仪或者GPS-RTK 测出其坐标。 普通的单开道岔结构如图1 所示。 确定岔心时,应先确定道岔型号,进而确定该型号的前端长a,由两轨缝连线的中心,沿线路中线量取a 值,即可定出道岔中心的位置。

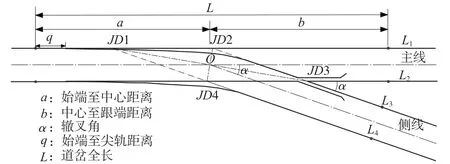
图1 道岔结构

从上述测量过程中可以看出,现有岔心测量方法存在以下不足:①岔心位置需要通过现场丈量确定,测量结果易受人为误差影响,测量精度难以保障;②需要测量人员在既有线路上作业,安全隐患较大。

三维激光扫描技术可以通过非接触的测量方式快速获取被测物体表面高精度、高密度的三维点云信息[1],克服了传统测量方法数据获取效率低、容易受环境条件限制及难以准确表达复杂目标真实情况的缺点,目前已广泛应用于矿区、滑坡及建(构)筑物等的变形监测当中。 如王黎明等分析了三维激光扫描技术应用于巷道变形监测的优势[2];戴华阳等基于三维激光扫描技术,提出应用房屋特征点提取采动区房屋移动变形的方法[3];徐进军等采用三维激光扫描技术进行高危边坡监测,完成了目标区域三维模型构建、大比例地形图及横纵断面图绘制、DEM 模型建立等测绘工作[46]。

在国内铁路既有线测绘领域,三维激光扫描技术的应用尚处于起步阶段。 将三维激光扫描技术引入既有铁路道岔测量中,不仅可以快速获取高精度的测量数据,还能有效规避测量人员既有线作业的风险。 以下根据铁路道岔的结构特点,对基于三维激光扫描技术的岔心测量方法进行研究。

1 数据采集及预处理

1.1 数据采集

三维激光扫描系统主要由扫描头、控制器和计算机三部分组成。 其中,扫描头包括激光发射器、接收器、水平反射镜和垂直反射镜;控制器包括距离测量模块、扫描控制模块以及计算机总线;计算机主要包括微处理器和存储器。

三维激光扫描系统的工作原理如下:激光发射器对扫描目标发射激光束,系统通过计算激光往返的时间差或相位差得到测量距离S,扫描控制模块记录激光束在垂直方向的旋转角度θ 和水平方向的旋转角度α,并据此计算出被测物体上点云的三维坐标(X,Y,Z)。

三维激光扫描仪一站的扫描范围有限,无法一次性将整个站场区域囊括进来,需要对站场区域进行分站扫描,因此,扫描后,需要对各站的扫描数据进行拼接。 本次实验所使用的扫描仪采用类似全站仪的设站方式,即将仪器架设在已知点上,扫描得到的各测站点云数据坐标系统一,不需要进行点云拼接,免除了拼接过程中的误差。

采集站场原始数据前,应首先选择扫描仪设站位置,并测出各站点的坐标,然后将三维激光扫描仪架设在已知站点上,在仪器中输入测站点坐标及仪器高,并设置好后视方向及各项扫描参数。 在扫描过程中,应及时查看已获取的点云数据,发现有漏掉的区域应及时补测。

1.2 数据预处理

点云数据预处理包括粗差剔除、数据裁剪、数据重采样3 个过程。

(1)粗差剔除

在野外数据采集时,不可避免地会存在一些明显的无效点,这些点即是点云数据中的粗差,需要通过扫描仪自带的数据处理软件进行剔除。

(2)数据裁剪

2017年入围中国最好大学排名前100强的9所医药类院校，整体上代表着医药类高等教育的竞争力水平，通过分析这9所高校的排名情况，可以找出其优势与不足，为长期的发展找到突破点。全国排名中，仅有首都医科大学入围前50强，其余8所高校均在50～100名之间，其中北京协和医学院与天津医科大学的名次接近，两所高校的综合竞争水平相当。单项指标全国排名中，9所高校在培养结果、科研质量、科技服务和成果转化指标上的排名远远落后于综合得分全国排名，在其它单项指标的排名上也不具有明显的竞争优势，这很大程度上限制了其在全国排名中的竞争力。(详见表4)

三维激光扫描仪获取的点云数据量极为庞大,其中相当一部分点云数据是我们不感兴趣的,可以将这些点云数据裁减掉,这样可以大大提高数据处理速度。如接触网杆、信号机、警冲标等与岔心提取关系不大,在数据预处理过程中,需要通过数据处理软件将非道岔点云数据裁剪掉,只保留道岔点云数据。

(3)数据重采样

扫描仪获取的原始点云数据密度不均匀(三维激光扫描仪发射的激光会随着距离的增加而逐渐发散,相邻两测站扫描重叠区域的点云密度又明显大于其他区域)。 因此,在进行数据预处理时,需要对原始数据进行重采样,以使点云密度尽量均匀。

应用三维激光扫描仪自带据数据处理软件对原始点云数进行上述预处理以后,就可以将道岔点云数据导出,保存为绝对坐标X,Y,Z 的格式。

2 轨面数据滤波

岔心坐标的获得主要通过提取钢轨直线来实现。因此,轨道的枕木等附件可以提前滤除掉,只保留钢轨的点云数据,这样可以极大地减少数据量,提高数据处理效率。 根据铁轨轨面高于枕木及道砟的特点,利用轨面高程进行滤波。 首先搜索点云数据中各点Z 坐标的最大值Zmax(Zmax即为轨面高程),设置滤波阈值h,点云数据中高程小于Zmax-h 予以剔除,高程大于或等于Zmax-h 的点作为轨面数据予以保留。 为了保证滤波效果,h 的取值宜在5 ～18 cm 之间。

图2 为轨面高程滤波前的点云数据, 共有85 177个点,数据量较大,且数据中存在枕木、道砟等点云信息,影响轨面直线的提取。 图3 为滤波后的点云数据(只剩3 823个点),有效地剔除了枕木、道砟等不必要的数据,保证了后续轨面直线提取的精度。

图2 轨面高程滤波前的点云数据

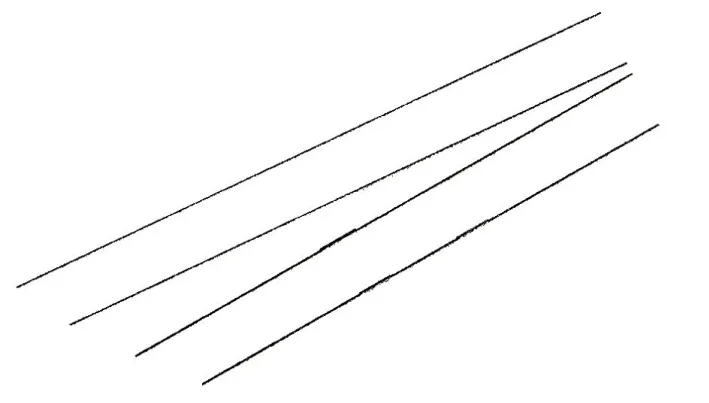
图3 轨面高程滤波后的点云数据

3 直线检测

如图3 所示,滤波后的点云数据投影到平面上表现为4 条钢轨轨面形状。 但由于点云数据散乱无序,无法确定每个点属于哪条钢轨,此时尚不能直接拟合钢轨中心直线。 在精确拟合直线参数之前,需要对滤波后的点云数据进行直线检测,以确定点云数据中的每个点属于哪条直线,然后才能对属于同一条直线的点云进行处理,并精确拟合直线参数。

采用Hough 变换算法对滤波后的点云数据进行直线检测,将属于同一条直线的点存储到相应的数组中。 其基本思想是利用点线对偶特性将图像空间中边界检测问题转换为参数空间中的累加统计问题。 利用Hough 变换检测直线时,直线方程表示为

(1)参数空间离散化。 确定参数ρ 和θ 的取值范围,以一定的间隔Δθ 和Δρ 将θ 和ρ 离散化,得到θi(i=1,2,3,…,m)和ρj(j=1,2,3,…,n)。

(2)建立参数空间的累加数组A(ρ,θ),用于存储一条直线上点的个数,并将每个数组元素置为0。

(3)遍历θ 在取值范围内的所有值,将原图像空间中的每个点带入直线表达式,求出相应的ρ,若ρ=ρj,则相应的累加数组A(ρj,θi)加1。

(4)为累加数组A(ρ,θ)设定一个阈值T,当A(ρj,θi)＞T 时,则ρj和θi即为要检测直线的参数。

在Hough 变换过程中,θ 的取值范围为[0°,180°]。 ρ 的最大值为变换域内到原点的最大距离。设变换域内x 和y 的最大值分别为xmax和ymax,则ρ 的取值范围为

4 直线参数拟合

为了提高直线提取的精度,采用最小二乘法对Hough 变换检测出的直线点集进行拟合,计算出直线的初始斜率k0和初始截距b0,设直线方程为y=kx+b,共线点的数量为n,可根据最小二乘原理拟合直线的斜率和截距,有

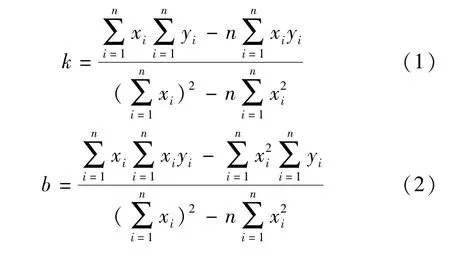
拟合出的直线效果如图4 所示。

图4 最小二乘法初次拟合

Hough 变换是图像处理领域中用于直线检测的一种常用方法,可将其引入到点云数据处理中,即Hough变换的处理对象由图像像素变为散乱点云。 铁轨轨面具有一定的宽度,利用Hough 变换检测出的直线往往不是1 条,而是斜率和截距相近的直线束。 图5 为将图4 局部放大后的效果,可明显地看出,Hough 变换提取出的直线并不是1 条。

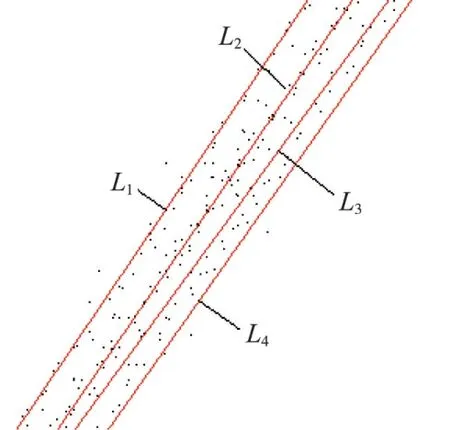
图5 Hough 变换检测出的直线束

使用Hough 变换检测点云数据中的直线特征时,往往先对点云数据进行边缘检测,然后再进行Hough变换检测,即可得到唯一直线。 然而,求取岔心坐标需要提取的是铁轨轨面的中心线而不是轨面的边缘,故不能对点云数据先进行边缘检测再提取直线特征。 为了提取铁轨中心线,需要将所有表示轨面的点云数据作为同一条直线上的点集进行处理。 因此,对于Hough 变换检测出的每条直线,需要重新筛选直线点集并进行拟合处理。

从图5 中可以看出,Hough 变换检测出的多条直线虽然参数不同,但是均分布在表示同一条轨面的点云数据中。 根据直线束的这一特点,为每一条直线设置一个邻域,将直线两侧邻域内所有点均作为表示该条直线的点集,然后采用最小二乘法对该点集进行拟合,即可得到表示该点集的最佳直线。 当每条直线的邻域设置得足够宽,可以将表示轨面的点云数据全部涵盖时,图5 中各条直线的直线点集就包含了表示轨面的所有点云。 该过程的具体实现步骤如下:

(1)选取第一次最小二乘拟合得到的直线初始斜率k0和初始截距b0作为初始直线参数。

(2)为直线设置一个具有一定宽度的邻域,重新筛选同属于这条初始直线的共线点集,直线邻域宽度设为d0。

(3)对于每1 条直线的初始参数(k0,b0),遍历所有点,计算点到直线的距离d,当d＜d0时,认为该点位于直线的邻域内,属于这条直线的直线点集,将其存储到相应的直线数组。

(4)对重新筛选出的直线点集进行最小二乘拟合,得到该直线的最新参数。

(5)将每条直线二次拟合得到的相近直线参数取平均值,即可得到表示铁轨轨面的中心直线。

需要注意的是,为了使每条直线的邻域尽可能包含同一铁轨上的所有点云,直线邻域宽度d0的取值应大于铁轨轨面的宽度。 点(x0,y0)到直线(y=kx+b)的距离d 可按照式(3)计算

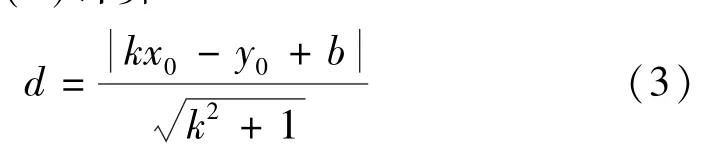
5 岔心计算

由图4 可知,每组道岔可提取出4 条轨道直线L1、L2、L3、L4,将4 条直线延长并两两相交,可以得到4 个交点JD1、JD2、JD3、JD4,4 个交点构成一个菱形,菱形中心O 即为岔心。 因此,根据式(4),可以由拟合出的直线参数计算出交点JD1、JD2、JD3、JD4 的坐标,将4 个交点的坐标取平均值,即可得到岔心的坐标。

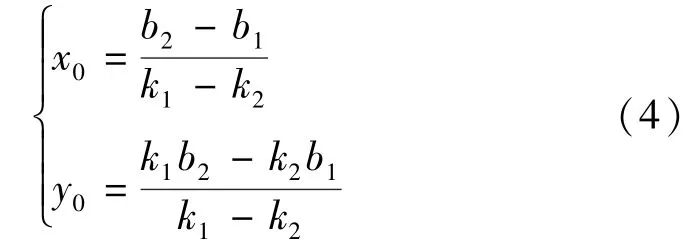
6 实例验证

为了验证该岔心提取方法的有效性,选取某车站5 组道岔的点云数据进行试验,分别计算5 组道岔的岔心坐标,并与传统人工测量方式取得的岔心坐标进行比较,实验结果如表1 所示。

由表1 可以看出,两种方法取得的岔心坐标差值较小,其中岔心坐标在x 方向上差值最大的为第5 组道岔,差值为1.8 cm;岔心坐标在y 方向上差值最大的为第4 组道岔,差值为2.7 cm。 该岔心提取方法的核心思想是基于Hough 变换,原始点云数据的密度不均匀性会造成岔心坐标提取结果存在一定误差。 从表1 中可以看出,采用该方法计算出的5 组道岔的岔心坐标与人工测量方式取得的岔心坐标差值均在3 cm 以内,可以应用于既有道岔岔心测量当中。 需要指出的是,该方法是基于直线延伸相交的原理计算岔心坐标的,只适用于直线形道岔,对于曲线形道岔并不适用。

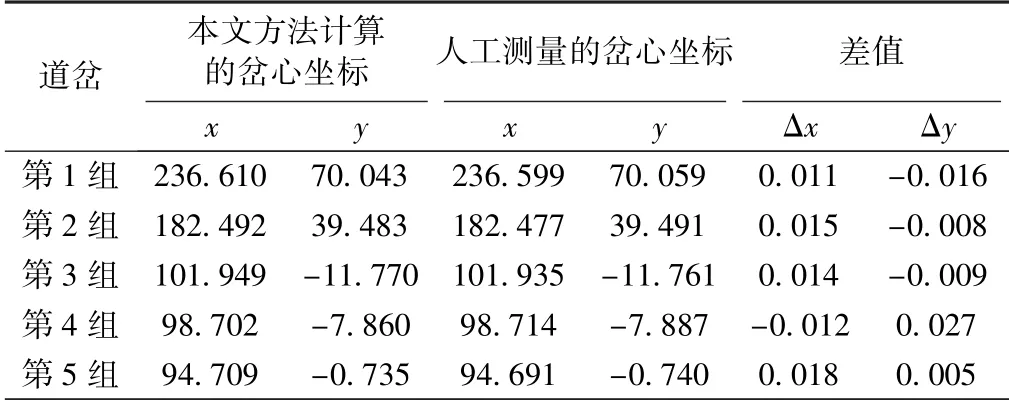
表1 实例验证结果 m

7 结束语

将三维激光扫描技术引入到铁路既有站场道岔测量中,提出了一种基于改进的Hough 变换和最小二乘拟合的方法,可自动从点云数据中提取既有道岔的岔心坐标。 选取某车站的5 组道岔数据对该方法进行验证,实验表明,该方法不仅可以自动计算出既有道岔的岔心坐标,大大提高了作业效率,而且有效规避了传统人工测量方式中测量人员上线作业的安全隐患,对于既有站场测绘技术的发展具有重要意义。