汽车低压导线热平衡建模与分析

陈 晨，杨 俭

（上汽大众汽车有限公司，上海 201805）

0 引言

汽车导线线径的匹配设计是线束系统开发的重要环节，线径的选择需考虑到系统的安全性与经济行，导线线径的选择需要以导体承载的电流的大小与电流的特性为依据，线径选取得过小，会造成导体温度过高，当温度超过自身耐温等级时，可能会发生燃烧［1］。而线径选择得过大则会造成导线成本过高，整车质量增加，安装布置难度增加，不利于成本的控制。通过建立导线热平衡模型，研究导体温度与加载电流、导线线径、环境温度等因素的关系，建立导线选型规则，可以更加可靠地进行线束系统的线径匹配设计。

在导体温度建模研究中，仿真研究是节省研究经费、缩短研发时间的有效途径。文献［2］通过分析不同工况散热情况建立了导体的瞬态温升模型，但是模型未经过试验数据的验证。文献［3］建立了考虑到导体、绝缘层及空气之间热传导的瞬态温升模型，建模考虑到了较多参数对导体温度的影响，并通过实验验证了模型的准确性，但是缺少关于模型应用方面的研究。

本文基于对导体热平衡关系分析，建立了导体瞬态温升模型，通过分析电流、导线线径、环境温度对导体温度的影响，推导出可用于导线选型的导体T-C特性曲线，且通过对比仿真与试验结果验证了模型的准确性。

1 导体电流特性分析

通过分析汽车线束承载的电流曲线特征，可将电流分为3种形式：稳定电流、脉冲电流、浪涌电流。图1为风窗加热电流曲线，通常电阻类的负载电流特征都为稳态电流。图2为起动机电流曲线，起动机工作时间只有0.4s，此电流特征认为是脉冲电流。浪涌电流可以看作是稳态电流与脉冲电流的叠加。本文分别针对这3种情况建立导体的热平衡方程。

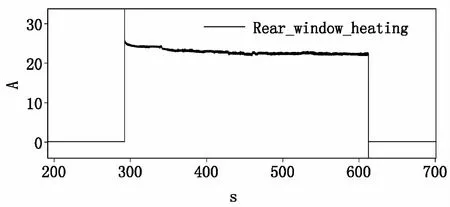
图1 风窗加热电流曲线

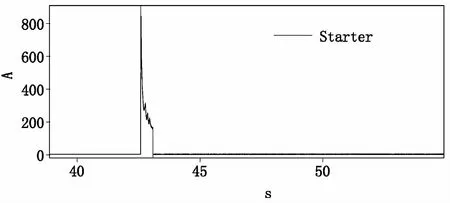
图2 起动机电流曲线

1）稳态电流：当导体承载长时间的稳定电流时，导体的温度会逐渐达到恒定值，此时导体的发热量与向环境中的散热量一致。

2）脉冲电流：脉冲电流往往作用时间比较短暂，导体温度可以近似看作不受环境温度的影响，即导体来不及向周围环境散热。

3）浪涌电流：是稳态电流与脉冲电流的叠加，电流中既有稳态电流，又有脉冲电流，实际情况中，大多数电流呈现为浪涌电流形式。图3为各类电流特性示意图。

图3 电流特性示意图

2 建模过程

2.1 建模假设

本文基于导体的热平衡建立温升模型，对导线结构进行一定的简化，如图4所示。同时模型有如下基本假设。

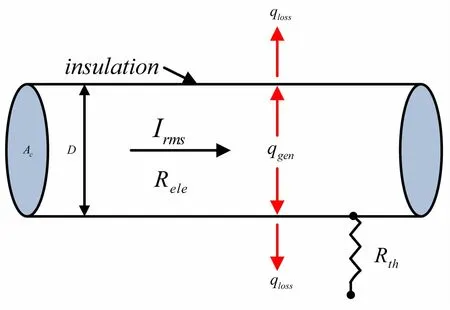
图4 导体热平衡模型示意图

1）导线半径忽略绝缘层厚度。在建立热平衡方程式考虑绝缘层对散热的影响，但几何上忽略绝缘层厚度。

2）模型假设整个导体横截面上的温度是均匀的，且所有的热传递 （或温度变化）变化发生在绝缘层与外部环境之间，即近似为集中热量体。

3）有效热传导系数视为恒定值，反映了热量从导体穿过绝缘层，传递至外界环境之间的阻抗。不同材质的有效热传导系数参考NEC［4］。模型忽略热辐射引起的热量传递，本文通过对有效热传导系数进行修正，来反映热辐射效应对热平衡的影响。

4）由于铜导线导电性能良好，且价格相对较低，目前汽车线束系统所用导线几乎都为铜导线，本文仅对铜导线情况进行分析。

5）仅考虑直流情况。

模型的基本参数定义见表1。

表1 参数定义

2.2 热平衡建模

导体中转化为热能的功率为导体制热功率减去散热功率［5］，如公式 （1）。基于热平衡方程，考虑3种常见电流形式，提出3种情况的热平衡模型。2

.2.1 稳态模型

当导体处于恒定的环境温度中，并加载恒定的电流时，导体的温度会逐渐到达平衡 （温度未达到绝缘层温度时），导体的温度会保持恒定。此时导体制热功率与散热功率相等时，如公式 （2）所示，其中制热功率与加载电流、导体电阻有关，散热功率与环境温度、热传导系数有关。求解方程得到导体的温度，如公式 （3）。

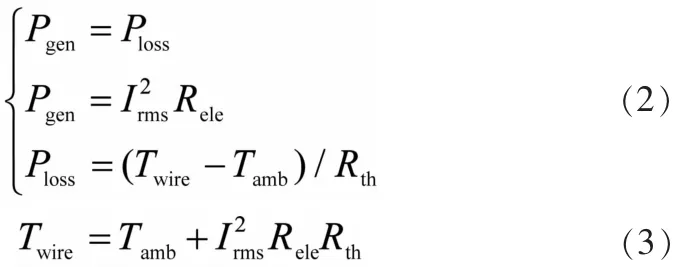
2.2.2 脉冲模型

当导体加载瞬时脉冲电流时，由于脉冲的时间比较短暂，导体向环境的散热可以忽略不计，此时可以认为导体制热功率全部转化为热能，如公式 （4），电流产生的热能全部用于导体温度的增长，如公式 （5）。导体温度会因脉冲电流而瞬间上升，电流归零后，温度缓慢收敛到环境温度。导体温度求解方程为公式 （6）。

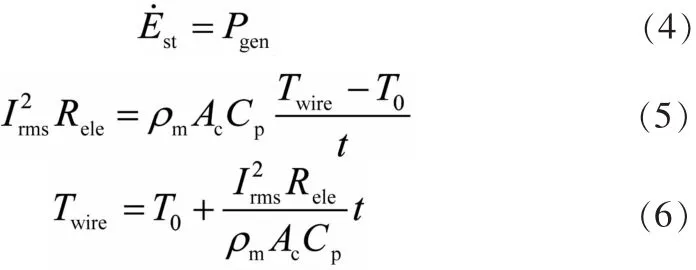
2.2.3 瞬态模型

当导体承载浪涌电流时，电流可以看作脉冲电流与稳态电流的叠加，用于温升的热量等于电流制热的功率减去导体向环境温度的散热功率［6］，平衡方程如公式 （7）。通过求解该一阶微分方程可得导体瞬时的温度，见公式 （8）。此瞬态模型同时可以考虑稳态电流和脉冲电流的情况。

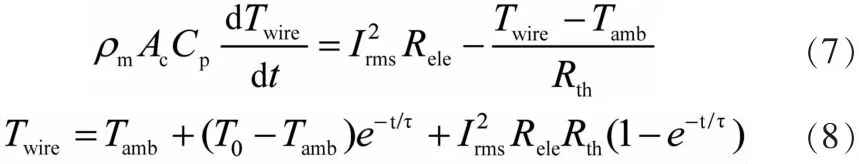
3 导线选型规则建立

3.1 模型仿真结果分析

利用建立的导体温升瞬态模型，考虑影响导线温度的电流、导线线径、环境温度等因素，分别分析其对温度的影响。由图5、图6、图7可以看出，电流的大小及导线线径会影响导体升温的速度，而环境温度对导体的影响主要是初始值的不同，对导体升温的速度影响不大。

图5 环境温度25℃，4mm2导线

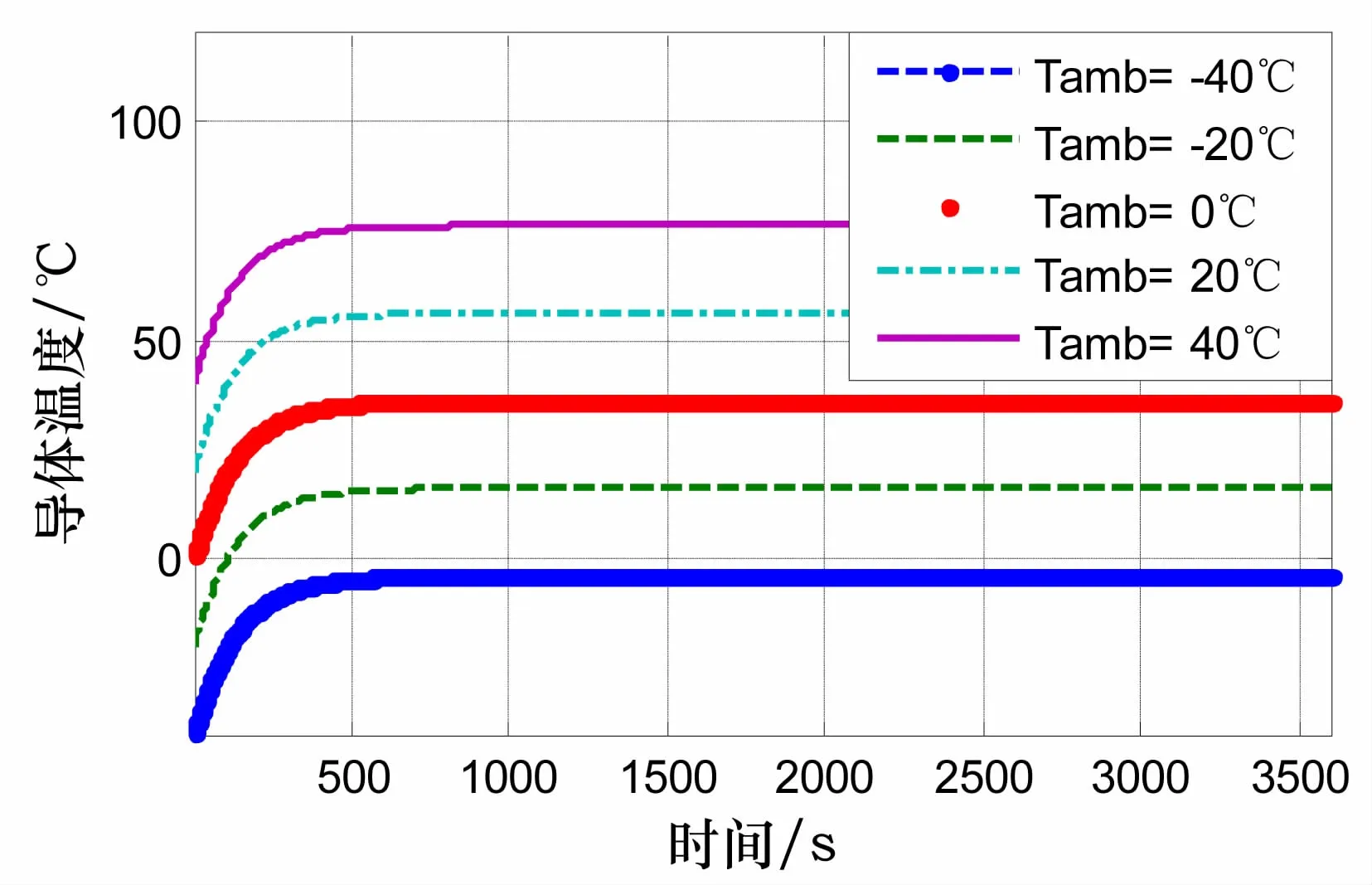
图6 恒定电流30A，4mm2导线

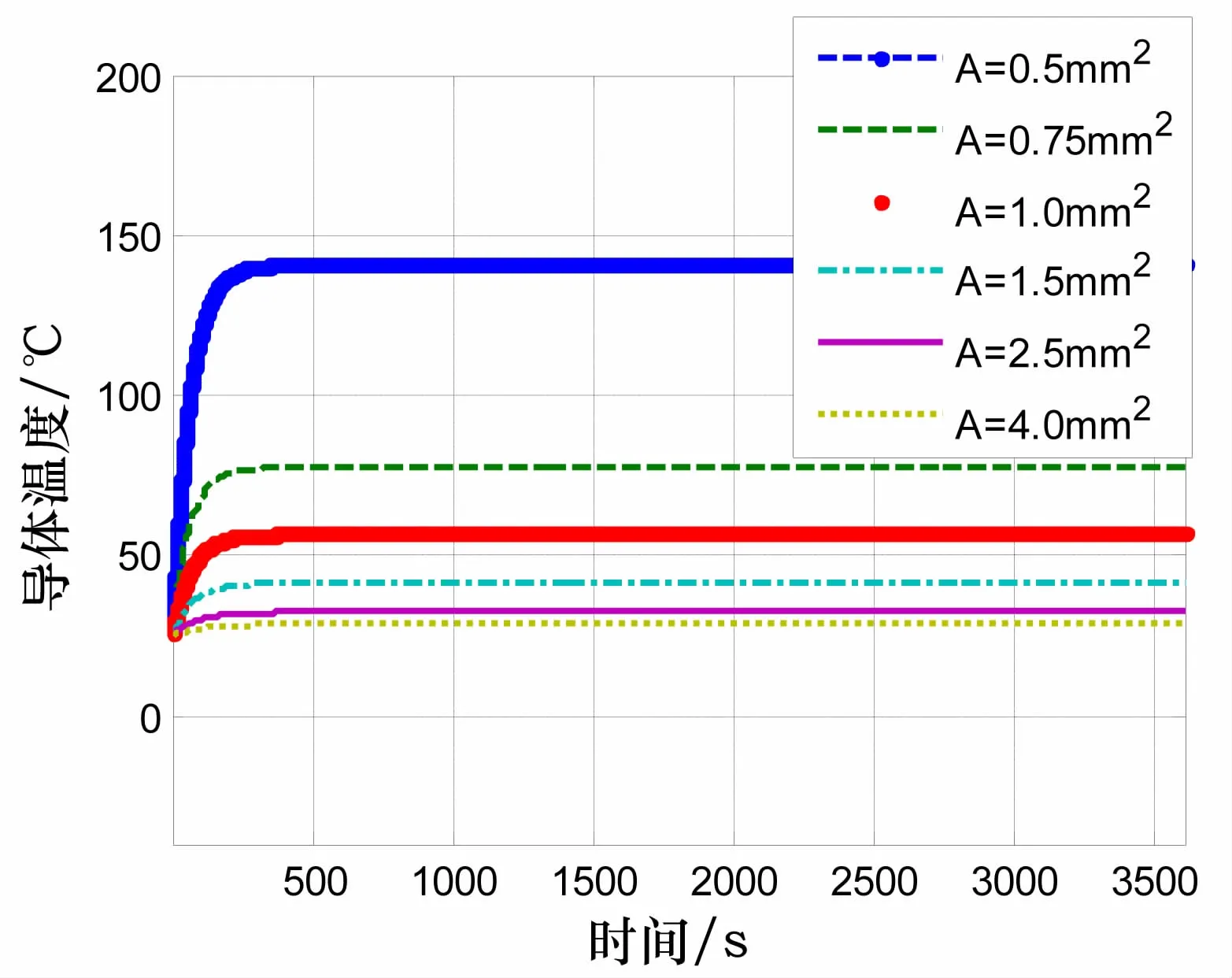
图7 环境温度25℃，恒定电流10A

3.2 T-C特性曲线

利用模型，已知导体绝缘层的耐温等级，可以求解得到导体温度达到绝缘层耐受温度的时间，如公式 （9），通过该公式可以分析不同线径、不同环境温度在一定电流情况下，导体温度达到绝缘温度的时间。

图8和图9为不同线径的导体在环境温度25℃情况下，导体的T-C特性曲线，横坐标为导体加载电流，纵坐标为导体到达绝缘层耐受温度 （此处为105℃）的时间。大线径导线在小线径导线的右侧，即曲线越往右耐受大电流的能力越强。图10为2.5mm2线径导线在不同环境温度下的T-C特性曲线。随着环境温度的升高，曲线逐渐向左移动，即导线耐受电流的能力逐渐变弱。

T-C特性曲线可用于导线选型的设计风险评估，即已知导线负载的电流信息，可由曲线查到导线达到绝缘层耐受温度的时间，对于长时间工作的用电器，电流值必须要在T-C特性曲线收敛值的左侧，才能保证导线长时间出于安全状态。

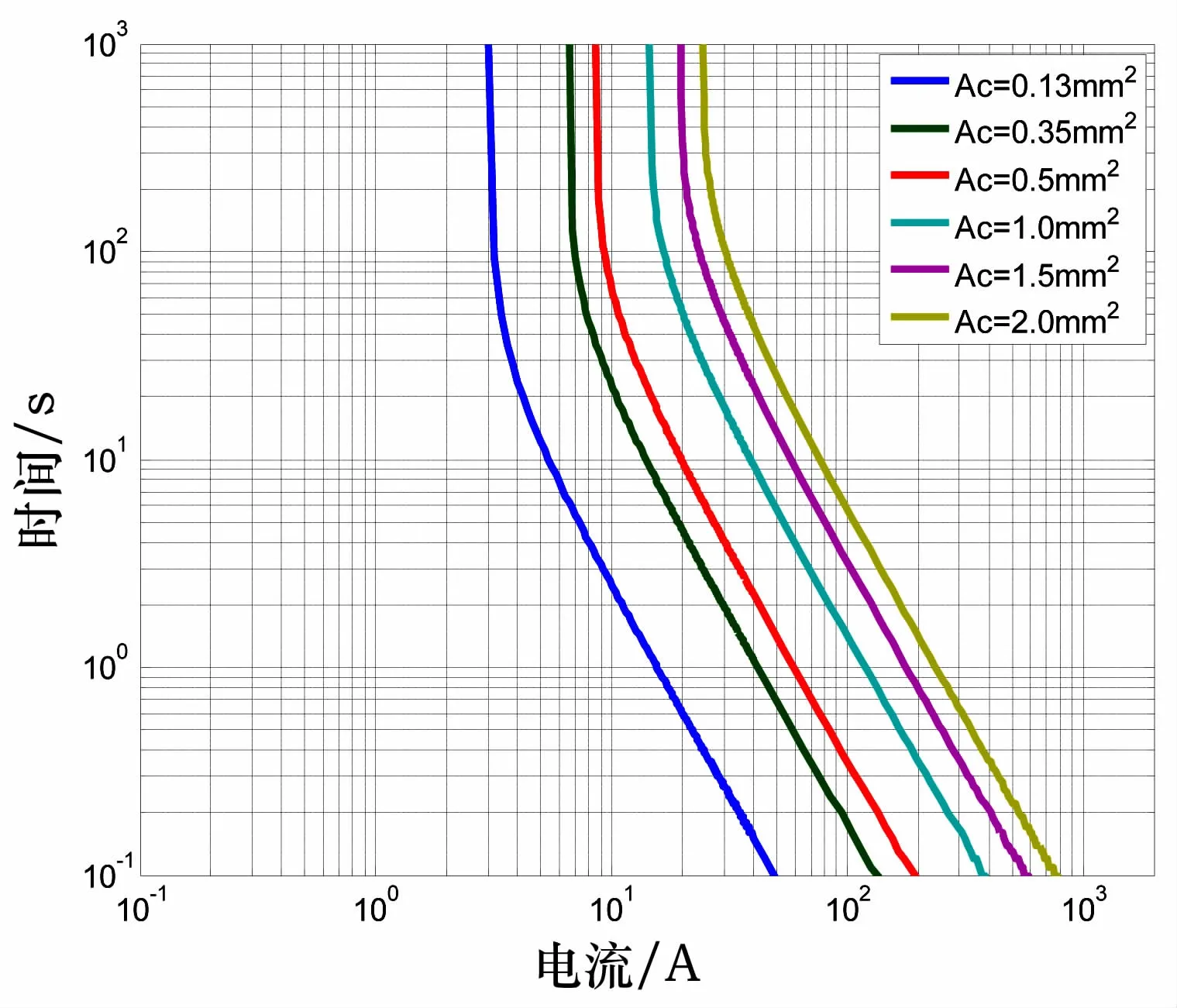
图8 不同线径T-C特性曲线1（环境温度25℃）

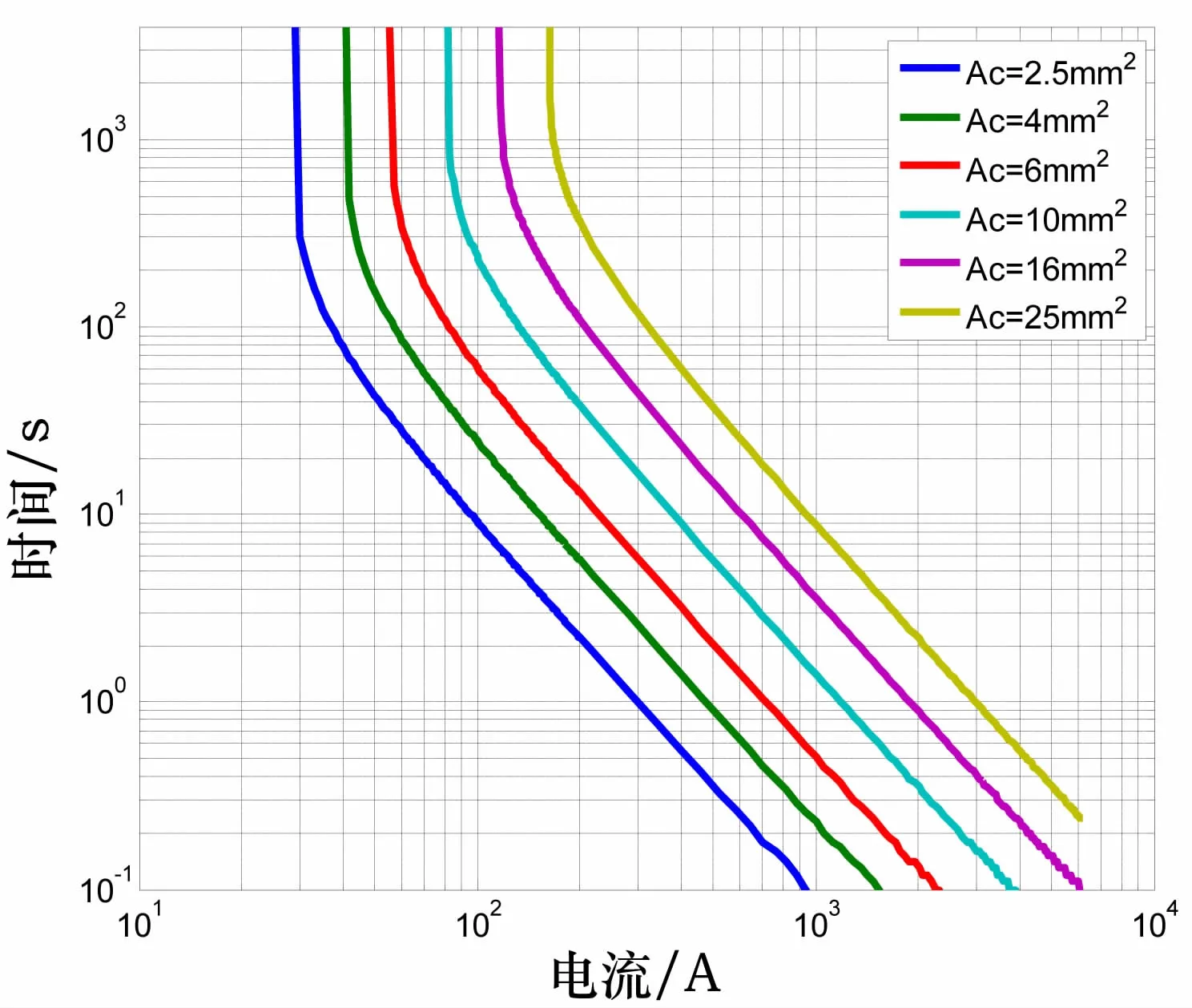
图9 不同线径T-C特性曲线2（环境温度25℃）

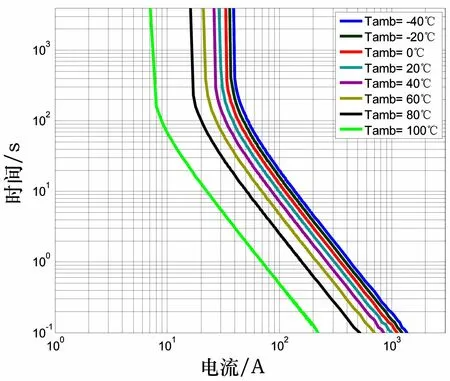
图10 不同环境温度T-C特性曲线 （线径2.5mm2）

4 模型验证

4.1 试验工况

基于某平台车辆线束，通过导线过载测试［7］验证仿真模型的准确性。导线加载电流大小为其熔断丝值 （30A） 的135%，即40.6A，图11为加载电流所使用的电子负载。利用K型热电偶，采集导线中金属导体处的温度，如图12所示。

图11 电子负载

图12 导线过载测试

4.2 模型结果对比

试验中同时利用K型热电偶采集环境温度数据，并将实际试验的环境温度数据和加载电流数据 （图13）作为模型仿真的输入信息，并计算得到导体的温度 （图14），由图可知，随着电流的作用导体温度逐渐增加，到达120s左右时间，电流停止，导体温度随之缓慢下降。导体计算温度与试验实测温度基本一致，模型的准确性得到验证。

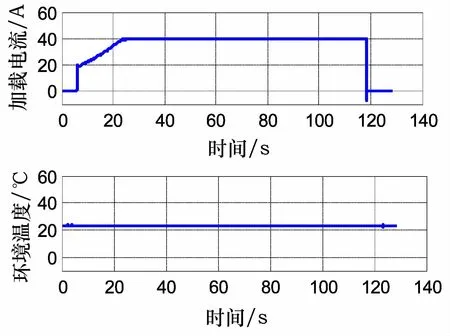
图13 试验环境温度及加载电流

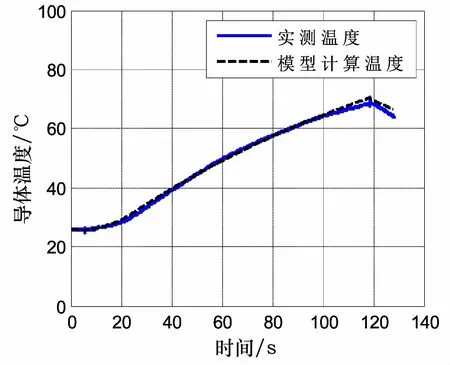
图14 导体试验与仿真温度对比图

5 总结

本文从分析汽车用电器常见电流曲线特征出发，建立了基于导体热平衡的导体瞬态温度模型，并仿真分析电流、导线线径、环境温度等因素对导线温度的影响。以辅助导线选型为目的，推导出可用于设计风险评估的导体T-C特性曲线，同时通过试验验证了模型的准确性。本文模型也可对其他材料导线进行分析，由于铝导线应用前景广泛，后续研究可以以铝导线作为基础进行展开。