整体式桥梁搭板连接及裂缝简化计算公式

朱溢敏，陈建伟

（宁波市城建设计研究院有限公司，浙江 宁波 315012）

0 引 言

整体式无缝桥梁的概念是从解决桥梁伸缩缝弊端中逐渐产生，而解决桥梁伸缩缝弊端最好的办法就是取消伸缩缝[1]。取消伸缩缝后桥梁的顺桥向变形随之传递至桥梁搭板末端；搭板作为路桥衔接段的重要组成部分，承担着减缓台后不均匀沉降的功能，搭板末端的纵向变形和竖向变形对搭板与桥台连接处的构造设计提出了新的要求。

以宁波惊驾东路3号桥整体式桥梁为例，提出该工程整体式桥梁搭板纵向变形和竖向变形解决措施及简化公式，并应用到该项目设计中。该桥于2018年竣工通车，至今已有一年时间，路桥衔接平顺，运营状况良好（见图1）。

图1桥梁竣工路面图

1 常规桥梁搭板连接构造设计

路桥衔接段不均匀沉降经常引起桥头跳车问题，在软土地区和高填方路桥衔接处尤为突出，常规桥梁通过设置搭板来解决此类问题。搭板一端通过锚栓钢筋与桥台牛腿进行铰接，与桥台间的空隙采用防腐木丝板或其他材料进行填充，另一端通过枕梁搁置在压实地基上。

常规桥梁在桥面板与桥台间设置伸缩缝装置，用以释放因温度、混凝土收缩徐变、活载等引起的桥梁纵向变形；搭板和桥台处设置锚栓钢筋形成铰接，用以释放不均匀沉降引起的竖向变形。

2 整体式桥梁搭板连接构造设计

与普通有缝桥梁一样，整体式桥梁搭板设计时需要考虑路桥衔接段不均匀沉降问题。搭板一端与桥台连接，与土接触的另一端由于附加荷载、填土沉陷等因素随之产生沉降，普通桥梁通过搭板锚栓钢筋连接桥台形成可变形的铰来适应两端产生的不均匀沉降。一方面搭板在锚栓钢筋处发生转动，进而通过铺装层发展到路面，形成局部裂缝，另一方面锚栓钢筋连接太薄弱，传递顺桥向的反复位移时可靠性有所下降，这种构造并不适合整体式桥梁。

整体式桥梁搭板与桥台连接处既要有刚度能传递桥面板的顺桥向位移，也要能适应不均匀沉降产生的转角变形，该连接处需采用介于刚接与铰接之间的构造措施[2]。设置混凝土铰是较好的解决办法，桥台至搭板标准段采用变截面混凝土，从A-A断面60 cm截面高度逐渐减少至35 cm，在B-B断面处钢筋面积最小（见表1），此处形成混凝土铰点。为了使转角变形引起的裂缝在混凝土铰附近均匀分布，在顶面设置多道深2 cm、宽2 mm诱导缝，减少单道裂缝张开宽度。构造大样如图2所示。

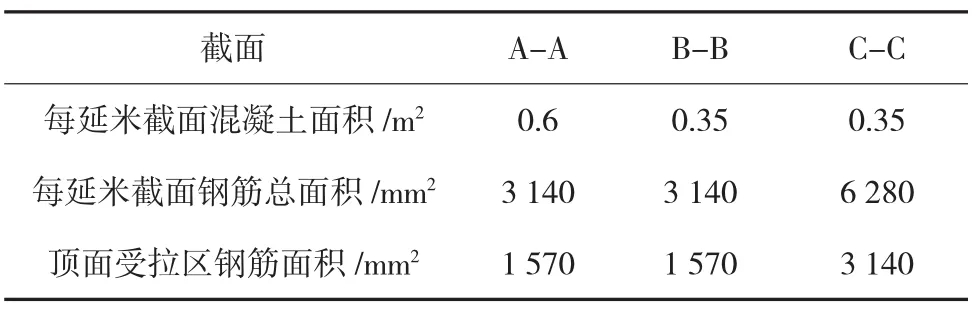
表1搭板连接处截面对比

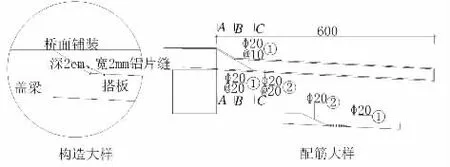
图2 搭板构造配筋图（单位：mm）

3 数值模拟分析

搭板与桥台连接后，搭板末端的工后沉降量对桥台与搭板连接处的转角以及可能引发的裂缝相关，同时也影响着搭板截面高度、长度、配筋量设计。为了能够真实模拟搭板末端沉降引起结构变形和内力，需根据搭板实际尺寸建立三维数值模型。使模拟尽可能符合真实情况，该次数值模拟的模型按如下原则建立：

（1）搭板模拟采用梁单元，截面高度为0.35 m，搭板长度为6.0 m，截面计算宽度取用1.0 m，材料采用C30混凝土。

（2）搭板与桥台连接端部模拟采用固定支座。

（3）搭板末端采用强迫位移（支座沉降工况）来模拟搭板末端工后沉降量。

采用midas Civil三维有限元软件建立搭板模型如图3所示。

图3 搭板模型图

搭板末端在模型计算时，工后沉降工况采用1cm、3 cm、5 cm、7 cm、9 cm进行模拟。工后沉降引起的搭板与桥台连接处弯矩值见表2。

表2 桥台与搭板连接处弯矩（每延米）

搭板末端工后沉降引起的连接区负弯矩进一步会引起搭板上表面受拉区产生裂缝，根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）第 6.4.3条[3]，连接区顶面配筋率按1.35%、0.90%、0.45%、0.30%对不同的工后沉降引起的负弯矩区进行裂缝计算，见表3。

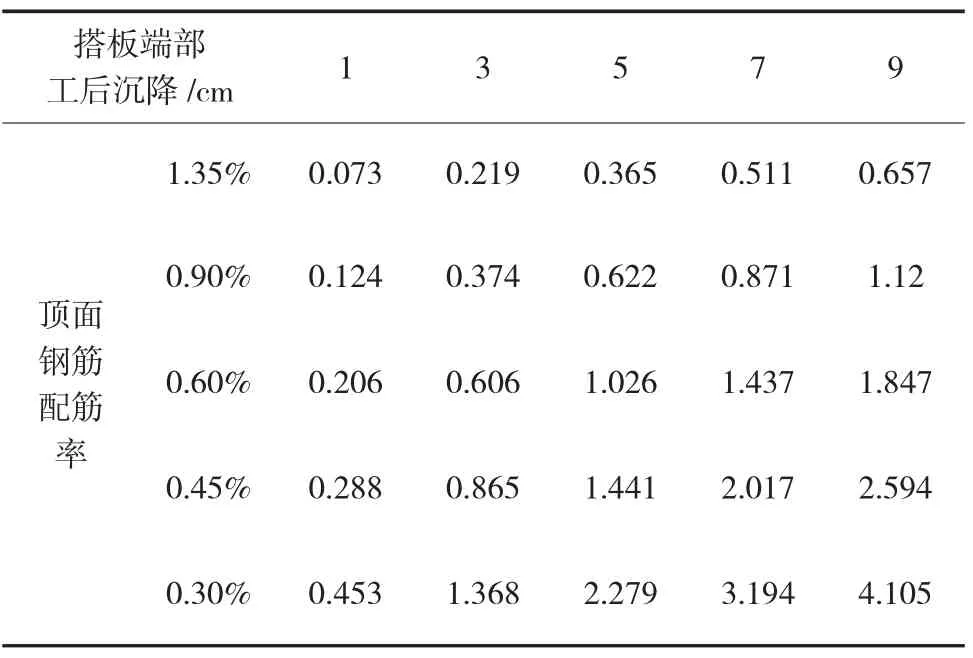
表3搭板顶面裂缝 mm

随着连接区顶板钢筋量的增加，顶面裂缝宽度逐渐变小，以搭板末端沉降5 cm为例，裂缝宽度从2.279 mm下降至0.365 mm。顶面受拉区配筋量在超过0.90%时，增加配筋量对减少裂缝的宽度影响逐渐降低，在不同的搭板末端沉降量的假定下，配筋量和裂缝宽度的相关曲线验证了这一点；但过小的配筋率（小于0.45%）会导致裂缝宽度过大，引起路面开裂，对于该桥梁中搭板与桥台连接处顶面配筋率在0.45%～0.90%较为合理，如图4所示。

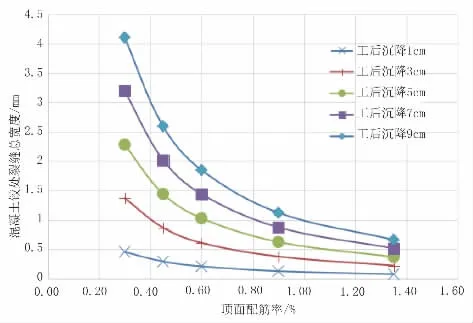
图4 连接区顶面配筋率与裂缝相关性曲线图

由于搭板端部的沉降，搭板与桥台连接处的裂缝是无法避免的，在不均匀沉降5 cm时，受拉区配筋率高达1.35%（24@100），裂缝宽度为0.365 mm，大于规范规定的0.200 mm裂缝宽度要求。

搭板与桥台间采用混凝土铰连接，采用降低的配筋率，合理布置诱导缝，使得裂缝在桥台与搭板连接区均匀分布，降低单道裂缝宽度，在理论上也证实了混凝土铰构造+多道诱导缝设置措施的合理性。

4 裂缝计算简化公式

搭板与桥台连接混凝土铰处张开裂缝总宽度与搭板末端不均匀沉降、搭板长度、搭板与桥台连接区截面高度、截面配筋率等相关。在几何上，搭板末端沉降Δ形成搭板与桥台连接处的转角α，进一步引起了连接区顶面的开裂，如图5所示。

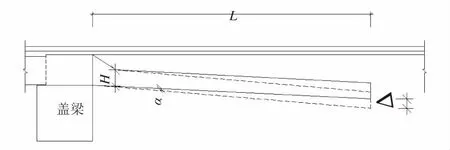
图5 搭板转动示意图

在方案和初步设计阶段等设计初期，台后地基处理、搭板构造尺寸、连接区配筋等尚未确定方案时，如果通过数值模拟进行计算，计算工作量和可比选方案将会增加较大的设计工作量，为更有利于整体式桥梁设计，可以通过一系列假定推导出计算搭板与桥台连接区裂缝的简化公式。

假定一：搭板处于单悬臂状态，混凝土铰处转角为Δ/L；而实际情况中，搭板底面支撑为弹性地基梁支撑，搭板本身并非完全刚体，搭板末端产生Δ变形时，搭板本身也能够适应部分变形量，而传递到混凝土铰处的转角实际上是小于Δ/L的。

假定二：搭板与桥台连接处的转角是绕连接处截面的中心位置进行转动的，裂缝总宽度B=αH/2；实际情况中，转动是绕截面假定中性轴发生转动的，A-A、B-B连接处顶面钢筋配筋量与底面钢筋配筋量相同，中性轴在截面中心位置；C-C连接处顶面钢筋是底面钢筋的2倍，中性轴位于截面中心上方，实际的裂缝总宽度小于αH/2。

假定三：搭板与桥台连接处配筋率在简化公式中直接表达，通过理论计算数值设置相关系数β，作为不同配筋率的影响因子。

故连接处单道裂缝平均宽度为

式中：Δ为搭板末端沉降，cm；L为搭板长度，m；α为桥台与搭板连接处转角，°；H为连接处截面厚度，m；β为连接区顶面配筋率的相关系数；n为搭板连接区顶面诱导缝数量；b为连接处单道裂缝平均宽度。

该工程连接区顶面合理配筋率为0.45%～0.90%，取用该桥梁工程的构造尺寸（H=0.35 m，L=6.0 m），B=0.291β，连接区配筋率取0.45%、0.60%、0.90%分别计算连接区顶面配筋率与裂缝总宽度B的相关系数，见表4。

表4 β拟合情况

根据β拟合数值，当配筋率为0.45%时，β可取1.0；当配筋率为0.60%时，β可取0.70；当配筋率为0.90%时，β可取0.43。

5 结 语

本文结合实际工程对整体式桥梁搭板连接构造设计进行了研究，该桥梁建成使用一年时间里，路桥衔接段未出现明显坡度变化和可见裂缝，行车平顺，可供类似整体式桥梁设计时参考。

桥梁与搭板设置混凝土铰+多道诱导缝措施能缓解台后不均匀沉降带来的转角变形，裂缝计算简化公式可供在拟定桥台地基处理措施、搭板截面尺寸、搭板长度、连接区配筋率时参考使用，简化设计的前期工作。

需进一步结合实际工程案例对简化公式进行分析对比，设置经验系数γ，以修正和完善简化公式，能更贴近实际工程的应用。