空间尺度信息的运动模糊核估计方法∗

唐 述, 万盛道, 杨书丽, 谢显中, 夏 明, 张 旭

(计算机网络和通信技术重庆市重点实验室(重庆邮电大学),重庆 400065)

由于成像系统的像差、散焦、大气湍流、噪声以及成像镜头与所拍摄场景的相对运动等众多因素的影响,不可避免地会导致拍摄到的图像出现模糊.近几年,随着相机的成像分辨率不断提高以及焦距范围的不断扩大,在引起图像模糊的众多因素中,由成像设备与被拍摄物体之间的相对运动所造成的图像运动模糊已成为图像模糊最主要的因素之一,因此,本文将主要针对场景静止,由相机的平面内平移所造成的单幅运动模糊图像的盲复原方法进行研究.在运动模糊图像的盲复原研究中,能否准确估计出引起图像模糊的运动模糊核(motion blur kernel,简称MBK)是能够复原出原始清晰图像的关键,而其中,图像有利边缘的准确提取和正则化约束项的合理设计,又是实现MBK准确估计的关键.2008年,Shan等人在算法的初始阶段先利用较强的正则化约束来选择幅值较大的强边缘来引导MBK的估计,然后随着迭代的进行再逐渐减小正则化的强度从而复原出丰富的图像细节,同时在对MBK的约束方面则采用了空间域的L1范数稀疏性约束[1].2009年,Cho等人采用双边滤波器、shock滤波器和一种梯度阈值策略来提取图像中幅值较大的强壮边缘,然后仅利用提取的强壮边缘对MBK进行估计,同时,Cho等人仅利用了简单的L2范数来对MBK进行稀疏性约束[2].2011年,Krishnan等人提出了一种L1/L2的正则化策略.该方法利用先前估计的潜在图像梯度的L2范数作为当前潜在图像梯度的L1范数的权重,可以被认为是一种归一化的L1范数[3].2012年,Li等人对MBK进行了全变差的正则化约束,并结合分裂的布雷格曼迭代,提出了一种扩展的分裂布雷格曼迭代盲复原算法[4].2010年,Xu等人的研究发现,与图像边缘的幅值相比,图像边缘的空间尺度更能决定MBK估计的准确性[5]——只有当图像中边缘的空间尺度大于MBK的尺度时,这样的边缘才会有利于MBK的估计(图像边缘的空间尺度是指图像中边缘的宽度,而MBK的尺度是指MBK的支持域的大小).2013年,Xu等人提出了一族损失函数来选择图像中的有利边缘,虽然这些损失函数能够较好地近似稀疏性最强的L0范数,但是在所选择的有利边缘中,绝大多数仍是由图像边缘的幅度值所决定的[6],并且该方法同样也是仅利用了简单的L2范数来对MBK进行稀疏性的约束.2013年,Pan等人将图像边缘的空间尺度信息结合到全变差的图像去噪模型中,实现有利图像边缘的准确提取,并提出了一种双重正则化约束模型来同时对MBK的稀疏性和连续性进行约束:空间域的超拉普拉斯分布约束MBK的稀疏性和梯度域的L0范数保证MBK的连续性[7].2016年,Pan等人根据图像暗信道的稀疏性,提出了一种基于暗信道先验的模糊图像盲复原方法[8].2015年,Ma等人提出了一种时间区域选择策略来提取模糊视频中每幅帧的有利图像结构,能够在有效去除视频运动模糊的同时实现视频的超分辨率重建[9].但是该方法仍然仅对MBK进行了简单的L2范数约束.2015年,Perrone等人提出了一种基于最大边缘分布的模糊图像盲复原方法,该方法通过在所有可能的潜在图像上进行最大化边缘分布来估计MBK[10].虽然该方法能够估计出较为合理的MBK,但是其计算量太大.2016年,Zuo等人提出了一种逐迭代的p范数正则化方法,并结合一种数据驱动策略来自适应地选择有利的图像边缘[11],该方法对于MBK则采用了超拉普拉斯分布来约束其稀疏性.2017年,Pan等人通过同时在图像的空间域和梯度域进行L0的稀疏性正则化约束来提取图像中的有利边缘,该方法同时也仅利用了简单的L2范数来对MBK进行稀疏性约束[12].

综上所述,现有方法存在的问题主要有:

· 一方面,在图像有利边缘的提取阶段,现有的绝大多数方法都是基于图像边缘的幅度值而非图像边缘的空间尺度信息[1−4,6,11,12].虽然Xu等人[5]提出了一种基于空间尺度的边缘提取策略,但是该方法对于用该策略计算出的边缘地图,仅采用了一种简单的阈值法(文献[5]中的公式(2)和公式(3)),从中选择出大尺度的有利边缘(在本文中,将空间尺度大于MBK尺度的图像边缘称为有利的图像边缘或者大尺度边缘;反之,将空间尺度小于MBK尺度的图像边缘称为有害的图像边缘或者小尺度边缘),因而并不能实现有利边缘的最优提取.另外,虽然Pan等人[7]也提出了一种结合空间尺度信息和全变差图像去噪模型的边缘提取方法,但是该方法的空间尺度信息地图仅是从观察到的模糊图像中计算得到的,而并没有在后续的迭代中进行更新(文献[7]中的公式(4)),并且该方法还存在计算量大和耗时多的问题.由此可见,现有的方法并不能真正准确地提取出图像的有利边缘.

· 另一方面,现有方法针对MBK正则化约束项的设计都过于简单,仅仅考虑了MBK的稀疏性[1−6,9,11,12],而忽略了MBK的连续性.虽然Pan等人[7]提出了一种双重正则化约束模型来同时对MBK的稀疏性和连续性进行约束,但是如前所述,该方法计算量太大,耗时太多.

由此可见,现有的方法并不能真正实现对MBK的准确估计,尤其是在严重运动模糊或者图像中纹理细节较为复杂的情况中,进而不能得到高质量的复原图像.

针对现有方法存在的两方面缺陷,本文提出了一种基于空间尺度信息的运动模糊核估计方法:首先,为了准确地提取有利的图像边缘,移除有害的图像结构,本文提出了一种基于图像空间尺度信息的图像平滑模型,提出的模型能够被有效的最优化求解,从而能够快速而准确地提取出最优的有利图像边缘;然后,从运动模糊退化函数的内在特性出发,提出了一种结合L0先验和L2先验的新的双重正则化约束模型来对MBK的稀疏性和连续性进行较好的约束,实现运动模糊核的准确估计,而且提出的双重正则化约束模型同样能够被有效地最优化求解.本文在客观的评价指标和主观的视觉效果上进行了大量实验,结果证明了提出的方法能够估计出更准确的MBK和复原出更高质量的去模糊图像.

1 提出的模糊核估计方法

图像的运动模糊可用如下的数学模型来表示:

其中,y为观察到的模糊噪声图像;k为未知的线性退化函数(blur kernel,简称BK);x为原始的清晰图像;n为零均值,方差为σ2的加性高斯噪声;*表示卷积运算.本文提出的方法采用了模糊图像盲复原领域常用的一种从粗到精的多尺度策略,并在每个尺度上都循环地执行以下3个步骤.

1) 有利的图像边缘的提取(useful image edges extraction,简称UIEE);

2) MBK的估计(motion blur kernel estimation,简称MBKE);

3) 中间潜在图像的复原(interim image restoration,简称IIR).

本文提出方法的流程如图1所示.

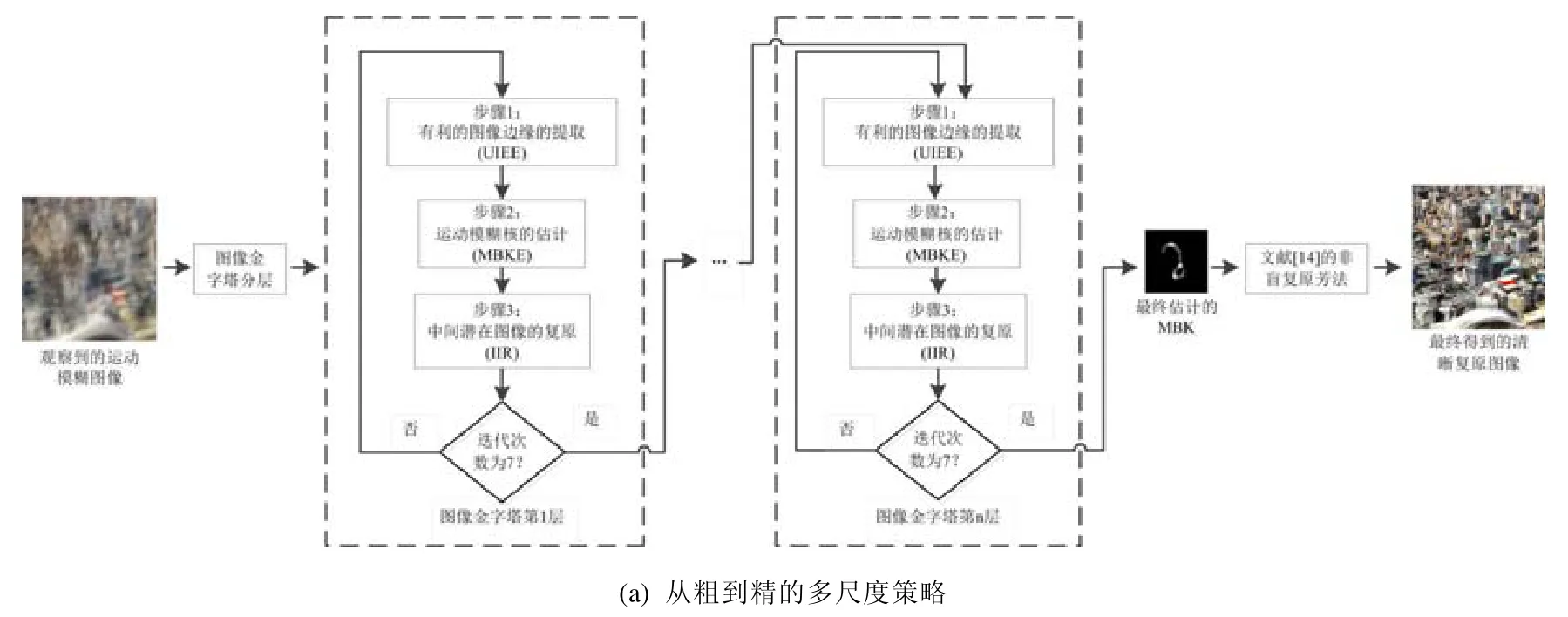
Fig.1 Overall process of our method图1 本文提出方法的流程

Fig.1 Overall process of our method (Continued)图1 本文提出方法的流程(续)

由图1可知,UIEE,MBKE和IIR是本文提出方法的关键.因此在接下来的章节中,本文将分别对UIEE,MBKE和IIR进行详细介绍.

1.1 有利的图像边缘的提取

如前所述,图像边缘的空间尺度更能决定MBK估计的准确性[5],因此,本文提出了一种基于图像空间尺度信息的图像平滑模型以实现图像有利边缘的准确提取:

其中,

·S表示结果图像;

·I表示输入图像,初始输入即为观察到的模糊噪声图像;之后,随着迭代的进行,输入则为中间的潜在复原图像;

·∇hS表示图像S在水平方向上的一阶梯度;

·∇vS表示图像S在垂直方向上的一阶梯度;

·ε为一个很小的正数,以防止分母等于0的情况产生;

·R(p)表示以像素点p为中心的局部矩形图像块.

从公式(2)的右边(第2项和第3项)可以得到:在图像块R(p)中,宽度小于R(p)宽度的图像边缘将会产生较大的Rh(Sp)值和Rv(Sp)值(因为在Rh(Sp)和Rv(Sp)的分母中,宽度小于R(p)宽度的图像边缘会产生成对的正负梯度值,这些成对的正负梯度值会在Rh(Sp)和Rv(Sp)的分母中正负相消);反之,宽度大于R(p)宽度的图像边缘会得到较小的Rh(Sp)值和Rv(Sp)值.因此,最小化Rh(Sp)和Rv(Sp)即可将宽度大于R(p)宽度的图像边缘准确地提取出来.由此可见,最小化Rh(Sp)和Rv(Sp)是一种基于图像边缘空间尺度的而非幅度值的图像边缘提取方法.于是我们得到:只要将图像块R(p)的宽度设置为等于或略大于MBK支持域的宽度,就能够通过最小化公式(2)将图像中的有利边缘准确地提取出来.公式(2)的第1项是为了保证输出图像和输入图像在内容上不会有较大的偏差.关于该模型的最优化求解,会在第2节详细给出.

1.2 MBK的估计

除了图像有利边缘的准确提取之外,正则化约束项的设计是影响MBK估计的另一个重要因素.Cai等人已经证明[13],运动模糊退化函数具有两种重要的特性:支持域的稀疏特性和连续特性.但是现有的方法针对MBK正则化约束项的设计几乎都仅仅只考虑了MBK的稀疏特性[1−6,8,9,11,12],而忽略了MBK的连续特性.虽然Cai等人提出了一种双重正则化约束模型来同时约束MBK的稀疏特性和连续特性,但是对于连续特性的约束,Cai等人却是对MBK进行像素值强度的高斯分布约束,即.然而,这类约束仿佛却更加偏向于稀疏的特性[2,5,6,12].虽然Pan等人也提出了一种双重正则化约束模型来同时对MBK的稀疏性和连续性进行约束,但是如前所述,该方法耗时太多[7].

通过对现有正则化约束项的分析,我们发现:直接对MBK的像素值强度进行稀疏特性的约束较为有效,例如,其中,0<α<1,;而对于连续特性的约束,在梯度域进行则比较有效,例如.即使L0范数是最稀疏的表示,但仍能够在梯度域中保证MBK的连续性[7].基于以上的分析,本文提出一种结合L0先验和高斯先验的新的双重正则化约束模型,对MBK的稀疏性和连续性进行较好的约束.

其中,γkc和γks分别表示连续性正则化参数和稀疏性正则化参数.由公式(3)可知:提出的模型将最稀疏的L0范数直接运用到MBK的像素值强度上,同时将具有平滑渐变特性的高斯先验运用到MBK的梯度域.因此,提出的模型能够很好地同时保证MBK的稀疏性和连续性.同样,在第2节会详细给出对该模型的最优化求解.

1.3 中间潜在图像的复原

在IIR阶段,本文采用了Krishnan等人提出的超拉普拉斯先验[14]来对中间的潜在图像进行复原:

其中,γI为正则化参数.本文直接采用了文献[14]中的方法来对公式(4)进行最优化求解.

2 对提出模型的最优化求解

2.1 基于空间尺度信息的图像平滑模型的求解

我们将分子中的|(∇hS)q|提取出来,并重新排列像素,得到:

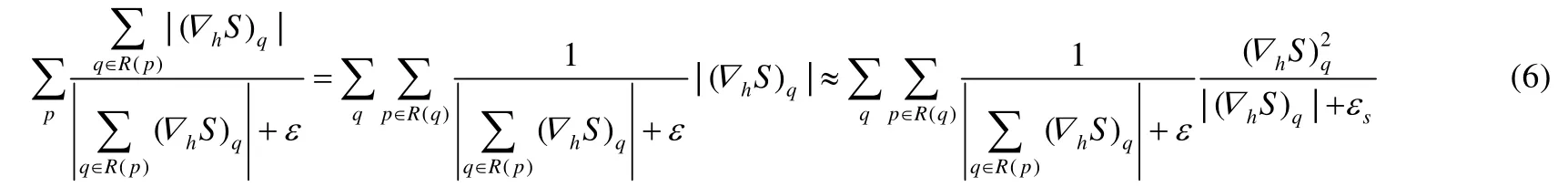
其中,εs为一个很小的正数,防止分母等于0.接下来,令

2.2 双重正则化约束模型的求解

由公式(3)可知,提出的双重正则化约束模型引入了一种离散的计数测量,即||k||0=#{p||kp|≠0},因此,我们采用了一种与文献[16]相类似的半二次性分裂的交互式最优化策略对提出的模型(公式(3))进行最优化求解.首先引入一个辅助变量bk,并引入一个额外的约束:bk=k,那么公式(3)被转换为

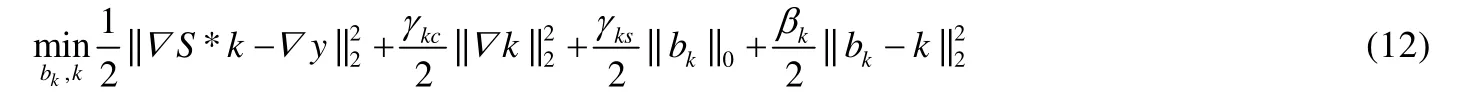
其中,βk为惩罚参数.接下来,我们将交互式地迭代求解k和bk.

· 固定bk,那么k可通过求解下式得到:

公式(13)对于k是二次性的,因此可在频率域求其闭合式解:

其中,F(⋅)和F−1(⋅)分别表示快速的傅里叶变换和快速的傅里叶逆变换,表示F(⋅)的复共轭,◦表示逐元素相乘操作.

· 固定k,那么bk可以通过求解下式得到:

公式(15)是一种逐元素的最小化问题,因此bk由下式可得:

同时,还在每次迭代中对MBK进行了归一化和非负的约束:

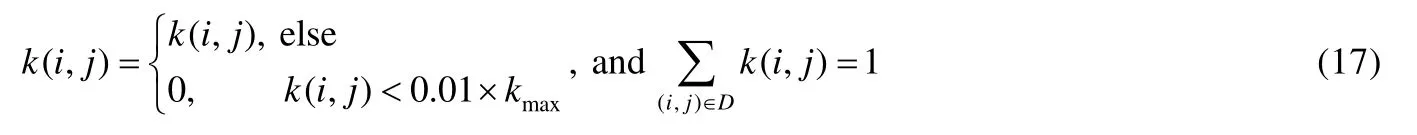
其中,D表示模糊核支持域的大小,kmax表示k中最大的元素.

本论文的方法将最低尺度的模糊噪声图像ycoarsest作为算法的初始输入值;同时,bk的初始值设为0.最终,一旦MBK被最终估计得到,我们就采用文献[14]中提出的基于超拉普拉斯先验的非盲复原方法来得到最终的清晰复原图像.

3 实验及分析

本文在客观的评价指标和主观的视觉效果上进行了大量的比较实验(分别与文献[2]、文献[3]、文献[5−7]和文献[11]的方法进行了比较)来验证提出方法的优越性.在客观的评价指标方面,本文分别采用了峰值信噪比(peak signal-to-noise ratio,简称PSNR)[6]和逆卷积错误比率(ratio between deconvolution error,简称RBDE)[6]来衡量所有盲复原方法的性能.实验所用的计算机具有8G内存和2.3GHz的双核Intel处理器.所有图像的像素值都被归一化到0～1之间.由公式(4)、公式(7)和公式(12)可知,提出的方法一共涉及到6个参数:εs,εs,γkc,γks,βk和γI.对于参数γkc和γks而言,参数γkc决定了MBK的连续平滑扩散的程度,而参数γks决定了MBK的稀疏程度,因此,γkc和γks共同决定了MBK估计的准确性.因为模糊图像中含有MBK的信息,因此在本文中,我们将γkc和γks的设置直接与模糊图像联系起来.经过反复实验,我们得到:在本文的所有实验中,γkc和γks分别被设置为参数βk控制着辅助变量bk与k之间的相似程度.在这里,本文采用了文献[16]中的方法来对参数βk进行设置:在算法的初始阶段,对参数βk设定一个较小的初始值;然后,在每次迭代之后对βk的值加倍,直到达到βk的最大值为止.参数βk的初始值为βk_ini=2γks,最大值为βk_max=105.ε和εs分别被设置为0.001和0.02.参数γI则遵循文献[14]的方法进行设置.为了实验的公平性,在MBK的估计阶段,实验中所有方法的实验结果都经过了大量实验,通过对每种方法中参数的反复调试而得到的最佳实验结果;而在最终的清晰图像复原阶段,所有方法均统一采用文献[14]的非盲复原方法来得到最终的清晰复原图像.

3.1 人造运动模糊图像的实验

在人造运动模糊图像的实验中,本文采用了文献[6]所使用的测试图像数据集和文献[17]的测试数据集.其中,文献[6]所使用的数据集为4幅255×255大小的灰度级清晰测试图像(如图2所示).而文献[17]的数据集为80幅大小不一的灰度级清晰测试图像.它们均采用了图3所示的8种不同的MBK来代表8种不同的运动模糊,共产生出了672幅人造的运动模糊图像.同时,本文在文献[6]的32幅运动模糊图像上还加入了均值为0、标准差为0.001的加性高斯噪声,而在文献[17]的640幅运动模糊图像上则加入了均值为0、标准差为0.01的加性高斯噪声.为了验证提出方法的优越性,将提出的方法与Cho等人的方法[2]、Krishnan等人的方法[3]、Xu等人的方法[5,6]以及Pan等人的方法[7,11]进行了比较.

Fig.2 Four grayscale test images of Ref.[6]图2 文献[6]所采用的4幅灰度级标准测试图像

Fig.3 Eight different MBKs图3 8种不同的运动模糊核

本文对所有的672幅人造模糊图像进行了比较实验,但是因为篇幅有限,在主观视觉效果的比较上,本节仅给出了Face图像在MBK4(最大的MBK)上的实验结果,如图4所示.

如图4所示,因为文献[2,6]中的方法是基于梯度的幅值来选择有利的图像边缘,同时,它们又只考虑了MBK的稀疏特性,因此,估计的MBK存在一定程度的噪声瑕疵,尤其是对于含有较多高对比度细边缘的Face图像.因此,文献[2,6]的方法所复原出的图像存在较多的ringing瑕疵(如图4(c)和图4(f)所示).基于L1/L2范数的盲去模糊方法所估计的MBK存在较为严重的间断,其复原图像存在较为严重的振铃瑕疵(图4(d)).虽然文献[5]中的方法是基于空间尺度的大小来测量图像中的有利边缘,但是所采用的硬阈值法并不能准确地提取出图像中所有的有利边缘,而且文献[5]也只考虑了MBK的稀疏特性,因此,文献[5]中方法所估计得到的MBK同样存在一定程度的噪声瑕疵和拖尾瑕疵,导致最终获得的复原图像不可避免地也存在一定程度的ringing瑕疵(如图4(e)所示).虽然文献[7]中的方法也是基于空间尺度来提取图像中的有利边缘,但是该方法仍然不能估计出准确的MBK:对于含有较多高对比度细边缘的Face图像,用该方法估计出的MBK趋向于delta函数,导致得到的复原图像没有任何的去模糊效果(如图4(g)所示).文献[12]中的方法也是一种基于图像梯度幅值的边缘选择策略,因此该方法所估计的MBK与文献[6]中方法估计的MBK相似,失真较为严重,因此其最终复原出的图像也不可避免地存在较多的ringing瑕疵(如图4(h)所示).相比之下,本文提出的方法因为实现了图像中大尺度有利边缘的最优化求解,同时利用L0先验和高斯先验很好地约束了MBK的稀疏特性和连续特性,因此本文提出的方法能够在很好地保证MBK稀疏性和连续性的同时有效地去除噪声和拖尾等瑕疵,估计出最准确的MBK,进而能够获得最高质量的复原图像(如图4(i)所示).

Fig.4 Recovered results and estimated MBKs of all methods with test image Face and MBK4图4 所有方法在Face图像和MBK4实验中的复原图像结果以及估计的运动模糊核

在客观的评价指标方面,本文分别采用了PSNR和RBDE来比较实验中所有盲复原方法的性能.图5表示所有方法在所有672幅人造运动模糊图像上的RBDE值.表1则表示在所有的672幅人造运动模糊图像中,每种方法在每个MBK上所得到的平均PSNR值.

图5中,横坐标上的数字2表示在所有的32幅人造模糊图像的实验中,满足RBDE<2的所有复原图像所占的百分比.已经证明:只有当RBDE<2时,得到的复原图像的质量才是可以接受的[6,7,17].如图5所示:本文提出的方法在RBDE<2的情况下达到了最高的70.7%,明显优于其余的6种盲复原方法.表1列出了在所有的672幅人造运动模糊图像中,每种方法在每个MBK上所得到的平均PSNR值.由表1可以明显地看到:在绝大多数情况下,本文所提出的方法能够获得最高的平均PSNR值(在所有的672幅人造模糊图像的盲复原实验中,6种MBK所获得的平均PSNR值达到了最高),明显优于其余6种盲复原方法.图5和表1从客观的评价指标方面证明了本文提出方法的有效性.

Fig.5 Percentages of the RBDEs of all the methods on all the 672 synthetic blurred images图5 所有方法在所有672幅人造模糊图像上的RBDE统计百分比

Table 1 Average PSNR (dB) values of each method for each MBK on all the 672 synthetic blurred images表1 在所有的672幅人造运动模糊图像中,每种方法在每个MBK上所得到的平均PSNR值

3.2 真实运动模糊图像的实验

除了人造的模糊图像之外,在本节中还将提出的方法运用到真实运动模糊图像的盲复原中.图6(a)为一幅大小为247×265的真实模糊图像(“structure”),MBK的大小为45×45个像素.该幅模糊图像包含有复杂的结构和丰富的小尺度边缘,具有一定的挑战性.

如图6所示,因为仅考虑了MBK的稀疏性,文献[2,5,6]中方法所估计的MBKs都含有或多或少的噪声瑕疵,其最后的复原图像具有显而易见的阴影瑕疵(如图6(b)、图6(d)和图6(e)所示).文献[3]无法估计出一个合理的MBK,导致最后的复原图像出现严重的失真(如图6(c)所示).文献[12]中方法估计出的MBK含有较为明显的噪声瑕疵,其最后的复原图像也存在于有显而易见的阴影瑕疵(如图6(g)所示).虽然文献[7]的方法能够估计出一个较好的MBK,但其最后的复原图像中仍含有一定程度的阴影效应(如图6(f)所示).相比之下,本文提出的方法在MBK的估计和最终图像的复原上都明显优于其余的6种方法.在MBK的估计中,本文的方法能够有效去除噪声等瑕疵,很好地保证MBK的稀疏性和连续性,因此能够复原出更加锐化的边缘和更多的细节,同时有效抑止阴影等瑕疵(如图6(h)所示).

Fig.6 Restoration results,estimated MBKs and the zoomed in regions of the real motion blurred image with complex structures and rich thin edges图6 含有复杂结构和丰富小尺度边缘的真实运动模糊图像盲复原结果,估计的MBK和局部放大图

图7(a)和图8(a)所示为两幅真实的严重运动模糊图像.图7(a)为一幅大小为728×470的真实运动模糊图像(“postcard”),其MBK的支持域为75×91个像素.图8(a)为一幅大小为685×561的真实运动模糊图像(“toy”),其MBK的支持域为95×95个像素.复原图像则呈现出令人不太舒服的过度锐化瑕疵(如图7(f)所示);相比之下,本文提出的方法能够在有效去除MBK噪声的同时,很好地保证其连续性,获得最准确的MBK,得到最高质量的复原图像(如图7(g)所示).

Fig.7 Restoration results,estimated MBKs and the zoomed in regions of the real large motion blurred image图7 严重的真实运动模糊图像盲复原结果,估计的MBK和局部放大图

Fig.8 Restoration results,estimated MBKs and the zoomed in regions of the real large motion blurred image图8 严重的真实运动模糊图像盲复原结果,估计的MBK和局部放大图

如图8所示,文献[2,5,6]中方法所估计的MBKs都含有噪声和断裂等瑕疵,其最终的复原图像也存在明显的ringing瑕疵(如图8(b)、图8(d)和图8(e)所示).文献[3]仍然无法估计出一个合理的MBK,导致最后的复原图像出现严重的振动(如图8(c)所示).虽然文献[7,12]的方法分别能够估计出较好的MBK,但是其最后得到的复原图像中仍含有一定程度的ringing瑕疵(如图8(f)和图8(g)所示).相比之下,本文提出的方法不仅能够估计出准确合理的MBK,而且能够明显抑制复原图像中的ringing瑕疵(如图8(h)所示);并且从局部放大图中可见,本文提出方法所复原出的边缘和细节也更加的清晰.

图6～图8从主观的视觉效果上证明了本文提出方法的优越性.接下来,我们将采用一种无参考的图像质量评价方法[18],从客观的评价指标方面进一步验证本文提出方法在真实运动模糊图像上的性能.表2为所有方法在真实运动模糊图像上采用文献[18]所得到的客观评价值,其中,数字越高,说明图像质量越好.

Table 2 Objective metric values of the methods[2,3,5−7,12] and the proposed methods for real motion blurred images Fig.6～Fig.8 by using Ref.[18]表2 文献[2,3,5−7,12]和本文提出方法在真实运动模糊图像上采用文献[18]方法所得到的客观评价值

由表2可知,本论文提出方法在真实的运动模糊图像(如图6和图8所示)中均能获得最高的客观测量值;在图7中则略低于文献[12]的方法.结合复原图像图7(f)和图7(g)可知,这或许是因为本文提出方法所得到的复原图像的对比度较文献[12]方法的复原图像的对比度较低所致.

除了主观和客观的比较之外,表3为文献[3,5−7,12]和本文提出方法在真实运动模糊图像的实验中估计MBK的时长.

Table 3 Processing times of MBK estimation of the methods[3,5−7,12] and the proposed methods for Fig.6～Fig.8表3 文献[3,5−7,12]和本文提出方法在图6～图8的实验中估计MBK的运行时间

由图6～图8、表2和表3可知,虽然本文提出方法估计MBK所需的时间略高于文献[5]中的方法,但是估计和复原的效果都有较大地提升.而相比其余的4种方法(文献[3,6,7,12]),本文提出的方法无论是在运行时间上还是在估计和复原的效果上都优于这4种方法,尤其是相比于文献[7]中的方法,运行时间呈数量级的减少.

3.3 散焦模糊图像的实验

为了验证本文提出方法的普适性,在本节中,将提出的方法运用到散焦模糊图像的盲复原中.在本次实验中,我们仅利用了人造的散焦模糊图像来验证本文方法的有效性,并且利用高斯核来模拟散焦的情况.实验采用了9×9个像素点大小,标准差为3个像素点的高斯模糊核和Kids图像(如图2(a)所示),结果如图9所示.

如图9所示,在散焦模糊的情况下,本文提出的方法并不能估计出准确的模糊核,也并不能复原出清晰锐化的图像边缘和细节.这有可能是因为对于散焦模糊而言,大部分的图像高频成分信息已经在模糊的过程中丢失了,而公式(2)只是对给定图像中大尺度边缘的提取,因此对于信息已经丢失了的散焦模糊图像,其提取出的也只能是不完整或错误的边缘信息,因此不能实现模糊核的准确估计,进而也就不能复原出高质量的清晰锐化图像.

Fig.9 Restoration experiment of defocus blurred image图9 散焦模糊图像的复原实验

4 结 论

本文提出了一种基于空间尺度信息的运动模糊核估计方法.首先建立一种基于图像空间尺度信息的图像平滑模型,并通过对约束项进行分解,实现了对图像有利边缘的最优化求解;其次,提出了一种结合空间L0先验和梯度L2先验的新的正则化约束模型来对MBK的稀疏性和连续性进行较好的约束,实现了MBK的准确估计.本文的方法在客观的评价指标和主观的视觉效果上进行了大量实验,结果证明了所提出方法的优越性.

但是,提出的方法还存在一定的局限性,例如含有饱和像素区域的模糊图像或者空间变化的运动模糊图像等,本方法就会失效,因为它们的模糊原理均违反了公式(1)中的均匀卷积操作.另一方面,本文提出的方法对于散焦模糊的图像也不能得到令人满意的复原结果.因此,将提出方法的思想运用到处理饱和像素区域和空间变化的模糊以及散焦模糊图像的复原,是我们接下来研究工作的重点.

致谢感谢Sunghyun Cho、Seungyong Lee、Li Xu、Jiaya Jia和Jinshan Pan等人提供了他们的方法的程序代码.