复用拉普拉斯算子的高效网格融合方法∗

金 耀 , 熊宇龙 , 周泳全 , 张华熊 , 何利力

1(浙江理工大学 信息学院 图形与数据智能研究所,浙江 杭州 310018)

2(深圳信息职业技术学院 机电工程学院,广东 深圳 518172)

随着计算机软硬件的迅猛发展,计算机辅助设计(CAD)、虚拟现实技术(VR)、增强现实技术(AR)得到了广泛应用,并逐渐融入人们的生活.如何高效地对虚拟场景进行建模,成为当前图形学领域的重要研究课题之一.在此背景下,交互式三维建模的方式越来越丰富,其中组装式建模,即通过部件组合的方式合成新模型,是一种低门槛、高效率的建模手段[1,2],受到人们的青睐;尤其是近年来与机器学习方法的结合[1,3,4],使其变得更为智能、高效与便捷,逐渐成为几何建模领域的一个研究热点.

组装式建模涉及的网格融合问题,是指将源网格与目标网格进行融合以合成新的网格模型.现有的主流方法大致可分为构造过渡曲面法与重建几何法.

· 构造过渡曲面法在源网格与目标网格边界之间构造了隐式曲面实现光滑拼接[5−8],这类方法适用多个复杂边界的融合,但隐式曲面(如径向基函数插值)通常需求解稠密矩阵方程且需网格化,较为耗时,因此往往难以达到交互响应速度;

· 重建法如经典的泊松融合[9]能够针对差异(形状、大小与顶点密度)较大的融合边界重建出可靠的源网格几何形状,但其旋转场与尺度场涉及测地线的计算,影响了效率,难以满足交互需求.为避免耗时的旋转场与尺度场计算,现有方法往往借助交互手段将源模型与目标网格进行对齐,然后运用代价较小的变形方法进行几何重建实现融合[10];为避免方程组的求解,进一步提高效率,变形过程采用了广义重心坐标法[4,11],但以增加交互量为代价.

为提高算法效率便于交互应用,同时尽可能减少用户的交互量,本文基于泊松融合框架,充分利用重构几何所用的拉普拉斯算子的性质,将几何重建、旋转场与尺度场的插值问题均转化为拉普拉斯(泊松)方程的求解,实现网格的高效融合.异于传统的局部变换(旋转与伸缩变换)传递方法,即通过计算权重场对局部变换进行局部线性混合插值,本文复用拉普拉斯算子将局部变换转化成若干个标量场进行全局插值;求解时,由于所用拉普拉斯矩阵是固定的,仅需预分解一次、通过多次耗时较少的回代计算快速获得8个标量场.此外,在进行网格融合时,用户通常希望网格附带的其他属性也能随之融合,因此本文针对带纹理坐标的模型,在几何融合时考虑了纹理坐标的融合,求解时亦通过复用拉普拉斯算子实现纹理坐标的快速更新,从而避免了纹理坐标的重计算.同时,本文还考虑了融合区域网格的优化问题.本文有3个贡献点:(1) 提出了一种基于复用拉普拉斯算子的高效几何融合方法;(2) 提出了一种基于复用拉普拉斯算子的高效纹理坐标融合方法;(3) 提出了基于Delaunay三角化与离散极小曲面的鲁棒局部网格优化方法.

1 相关工作

网格融合作为组装式建模的重要手段,在几何建模与处理领域一直受到人们的关注,并出现了大量的研究工作.现有的网格融合方法大致分可为两大类:构造光滑边界法与重建几何法.

构造光滑边界法类似于补洞算法,即:在源网格和目标网格之间构造一个过渡曲面,将两者光滑地连接起来.重点在于如何构造该曲面,其代表方法有配准法与构造过渡曲面法.配准法即将源网格与目标网格在边界处的重叠区域进行非刚体变换实现拼接.Sharf等人[12]提出了Soft-ICP方法,在重叠区域迭代地进行对应点搜索与配准.Kreavoy等人[13]采用交互方法对融合区域进行对齐,然后采用上述方法进行融合.Zhu等人[14]构造了一个公共边界,使其到目标网格和源网格的边界的距离平方和最小化,并计算一个权重场对其进行加权的拉普拉斯光顺.Liu等人[15]采用类似生成扫成体的方法构造过渡曲面.万华根[6]采用径向基函数构造变分隐式曲面进行插值,然后抽取等值面将其转化成多边形网格.Jin等人[7]结合径向基函数与有向距离场构造过渡隐式曲面.Lin等人[8]基于前述方法[6,7],采用勾画式交互手段勾勒过渡曲面轮廓线,以控制插值曲面的形状.缪永伟等人[16]则采用了Hermite插值曲面作为过渡曲面.总而言之,这类方法虽然能实现复杂模型的拼接与融合,但是由于构造过渡曲面计算代价较大,通常难以满足交互响应的要求.

几何重建法是根据源网格的几何信息重建出在新边界条件下的几何形状,并尽可能保持其几何度量,代表方法又可细分为参数化法与变形法.

参数化法将源网格与目标网格的融合区域参数化到一个共同区域,然后根据对应顶点的重心坐标插值重构几何.Kanai等人[17]在两个网格的融合区域边界进行对齐,并运用全局调和映射建立网格顶点的对应关系,并通过融合控制函数调整形状.Biermann等人[18]基于角度展平(ABF)参数化实现模型表面细节的迁移与融合,该方法被用于基于样例的建模[2]与基于最小割的网格融合[19].刘刚等人[20]在此基础上提出了基于局部调和映射的融合算法,利用等距线抽取待融合区域,更为简单、快速.Fu等人[21]同样基于该算法的思想,利用参数化编码表面细节,有效处理具有复杂拓扑的网格.但是参数化法对于具有复杂几何细节的源模型易引起较大的形变误差,从而导致重建效果不理想,且往往受到网格拓扑的限制而不适用于一般的网格.

变形法主要运用基于微分域的变形技术[22]重建源网格.泊松融合法[9,23,24]通过构造新的梯度场(一阶微分量)使之逼近原几何模型的梯度场,并求解泊松方程从新梯度场恢复其几何;拉普拉斯变形法[25]则利用了二阶微分量,通过拟合拉普拉斯坐标重建几何.两者均为后续的变形与融合方法产生了重要的奠基作用.变形法所涉及的一个重要问题为局部变换(旋转与伸缩)的传递,现有的方法往往通过构造光滑的权重场并运用该标量场进行线性混合将局部变换由边界处传递至网格内部.这种几何域标量场在几何处理中有着广泛的应用[26,27],其计算方法也较为成熟[28].如泊松融合法[9,24]采用测地线计算标量场,但极为耗时,使其难以满足交互响应.Zayer等人[29]提出用调和场替换测地距离场,提高了变形的计算效率,但是该方法需指定源(固定)和目标(编辑)顶点的边界条件,而融合问题仅给出源顶点而无法确定目标顶点,因此难以直接采用.为避免局部变换传递的计算,不少研究者预先将源网格与目标网格对齐,然后直接采用变形法进行融合.Deng等人[11]与刘骊等人[4]则采用了中值坐标求解泊松方程,改善了效率.Takayama等人[10]采用了两步变形法:首先,根据融合边界构造笼子,并基于笼子变形法重构源网格几何,使之与目标网格对齐;然后,用拉普拉斯变形法进行边界融合与细节恢复,但其笼子变形法对于复杂的源网格易产生不理想的变形效果.Qian等人[30]在此基础上提出了金字塔球面坐标,其鲁棒性得到了改善.

本文方法基于泊松融合框架,因此具有传统泊松融合法的优点,适用于边界差异较大的网格,且交互方式便捷,仅需在源网格与目标网格边界指定稀疏的对应点便能实现融合.本文利用全局拉普拉斯光顺法并多次复用拉普拉斯矩阵,实现旋转场、尺度场与几何坐标的高效计算,比起基于测地线的泊松融合法,避免了测地距离场的计算,提高了效率,使之适合于交互应用;比起中值坐标法,本文可自动调整模型的尺寸且拼接边界处过渡更为自然.此外,在现有的网格融合方法中,通常仅考虑几何坐标的融合,而较少同时考虑网格的其他属性的融合,如文献[31]提出的纹理图像的融合.据我们所知,在几何融合时考虑纹理坐标的融合的工作未曾见有报道.本文针对带纹理的网格模型,再次复用拉普拉斯矩阵,用较小的时间代价生成合成模型的纹理坐标.

2 泊松融合算法框架

泊松网格融合[9,24]的思想是在新边界约束下,用待重建模型的梯度算子拟合源网格模型的几何梯度场.设源三角形网格Ω为二维流形且表示为〈V,F〉,其中,V={vi}为顶点集(i=1,2,…,|V|),T={ti}为三角形面片集(i=1,2,…,|F|).为每个顶点vi赋予一个标量值f(vi)=fi,则网格Ω上定义了一个标量场,其上任意点v处的标量值为

其中,φi(⋅)为分段线性基函数.若将该标量函数定义为三维几何坐标x,y,z这3个分量,则泊松融合问题可描述为在边界约束下的向量场拟合问题:

其中,At是三角形t的面积,ft是待求网格面片t上的三个标量场,gt为目标梯度场.由于源网格与目标网格通常处于不同的局部坐标系,两个模型在摆放方向与尺寸上存在差异,因此,其对应的目标梯度场需要进行校正.在实际应用中,需将源模型三角形t上的梯度经过局部伸缩变换st与旋转变换Rt(根据两个网格的边界信息进行估计)使其位于目标网格坐标系下.

上述优化问题(公式(1))可通过对梯度场进行积分转化成泊松方程进行求解,进而重构出几何坐标:

其中,Δ是拉普拉斯算子,div为散度算子.由于f是分段线性函数、顶点i的拉普拉斯算子通常离散化为几何敏感的余切算子[32]:

其中,j遍历顶点i的1-环邻域顶点,αij与βij是网格边〈i,j〉的对角,ui,uj分别为顶点i与顶点j的标量值,L为拉普拉斯矩阵,u为网格顶点坐标分量形成的向量.若将边界顶点的位置约束转化为软约束,则泊松方程可离散化为对称正定的稀疏线性方程组:

其中,Lc=AL+λC.

·A为网格顶点的Voronoi面积构成的对角阵,其对角元表示为顶点1-环邻域三角形面积总和的三分之一:(j遍历顶点i的邻接三角形);

·C为位置约束的对角系数矩阵;

·λ为软约束权重,默认取作108.

综上,泊松融合算法的步骤可描述如下.

步骤1:设置源网格模型与目标网格模型边界顶点的对应关系;

步骤2:根据源网格与对应目标网格边界顶点信息计算局部变换——旋转变换与缩放尺度;

步骤3:计算源网格融合边界顶点到其他顶点的测地距离,并由此构造权函数标量场,根据该标量场,运用线性混合法插值出新边界下源网格上的旋转场与尺度场;

步骤4:根据步骤3得到的局部变换场计算新梯度场,运用泊松方程对该梯度场进行积分(公式(4)),并求解该泊松方程获得源网格模型在新边界约束下的几何坐标.

3 基于可复用拉普拉斯算子的融合

泊松融合的核心是求解泊松方程,其系数矩阵为拉普拉斯矩阵.拉普拉斯算子被称为几何处理的“瑞士军刀”[33],在几何处理领域有着广泛的应用背景,例如网格变形[9]、参数化[32]、光顺[27]、距离场计算[28,29]、形状分析[33]等.本文基于上述传统的泊松融合算法,充分利用拉普拉斯算子的优良性质,将融合中的若干问题,如几何重建、旋转场与尺度场的光滑插值、纹理坐标融合等,均采用拉普拉斯算子进行建模,使其多个计算步骤均可复用同一个拉普拉斯算子,从而减少计算时间,使其适合交互应用.

3.1 旋转场与尺度场的插值

融合算法步骤中,最为耗时的是步骤3,即旋转场与尺度场的插值.在计算旋转场时,由于旋转矩阵对加法运算不封闭,不能直接用于插值计算,因此往往需转化成四元素q=〈qx,qy,qz,qw〉,并在四元素空间进行插值.为得到光滑的旋转场与尺度场,文献[9]采用了线性加权法,即非边界顶点处的四元素qi与尺度值si表示为边界顶点处对应值的线性组合:

其中,ωij可取关于顶点i到j的测地距离的单调递减函数,通常可取倒数函数、高斯函数等.由此可见:为计算整个源网格域上的标量场,共需计算对测地线距离(VB为融合边界顶点集).因此,该方法不仅需借助一个大型稠密矩阵进行存储而耗费内存空间,而且由于测地线的计算非常耗时,限制了其交互应用.

局部变换场,尤其是旋转变换场的插值,是常用变形算法的一个重要环节.文献[29]在变形时,利用拉普拉斯算子的光滑性质,采用调和场作为权重场传递局部变换:构建一个拉普拉斯方程Δu=0,并由用户指定其边界条件,其中,在固定顶点处设置为0,在变形的编辑顶点处设置为1,则任意顶点处的变换可表示为固定顶点标量场与编辑顶点标量场的线性混合.该方法仅需求解一个线性系统,比起基于测地线的局部变换传递方法显著地减少了计算量.但该方法仅适合一般的变形应用,对于网格融合应用,由于没有约束顶点与可编辑顶点之区分,难以指定其边界条件,因而不能用于构造光滑的权重场.

异于上述根据边界标量场进行线性混合的思路[9,29],本文受到拉普拉斯光顺算法的启发[27],将局部变换场转化成5个标量场(四元素标量场qx,qy,qz,qw与一个尺度标量场s),并采用全局拉普拉斯光顺法对其进行平滑插值.即在新的边界约束下构造使得定义域上的标量场变化的能量和达到极小值的能量函数:

其中,约束条件为狄利克雷边界条件.因此,该问题的极小值可转化为拉普拉斯方程的解:

由公式(7)可见其形式与公式(2)相似,它们均可转化成公式(4)进行求解.由于标量场与几何坐标共享一个网格域,该方程的系数矩阵——拉普拉斯矩阵完全相同,并且它们的约束顶点相同,因此在求解时可重复利用这些信息.

求解公式(4)的对称正定方程可采用Cholesky分解法,即:将矩阵分解为一个下三角矩阵及其转置的乘积,即Lc=AAt(A为下三角矩阵),然后利用其三角阵特点进行快速回代计算,即:分别求解方程AY=b,Au=Y,得到方程最终的解u.对于线性求解器而言,它一般可分为3个步骤:结构分解、数值分解与回代.其中,结构分解与数值分解耗时相对最多,而回代计算耗时较少.利用该特点,本文多次复用拉普拉斯矩阵分解的结果,以加速计算上述8个标量场(3个位置分量场、4个四元素分量场与1个尺度场):对拉普拉斯矩阵进行一次结构分解与数值分解,然后执行8次回代计算.因此,比起基于测地线的标量场插值法,该方法通过复用拉普拉斯矩阵,避免了测地线的计算,不仅减少了计算量,也节省了存储距离场的空间.

3.2 纹理坐标的融合

对带纹理坐标的模型进行几何融合,往往希望融合结果的纹理坐标得到保持.但是若仅融合几何坐标,而简单地将源模型的纹理坐标“拷贝”至目标模型,则无法保持纹理坐标的连续性;若对合成模型重新计算纹理坐标,则不仅计算代价太大,而且将改变目标模型上原有的纹理坐标,这在某些场合是不允许的.为此,本文在考虑几何融合的同时,再次复用拉普拉斯算子实现纹理坐标的融合,以快速地更新源网格的纹理坐标,使之能够保持目标网格的纹理坐标并保证其连续性.

纹理坐标可通过计算网格参数化得到.参数化通常转化为极小化某种几何度量问题.这种几何度量可以是角度、面积、长度误差等,它们均与几何敏感的拉普拉斯存在着密切的关系.本文采用调和参数化,即求解如下拉普拉斯方程的解:

其中:Δ同公式(2)与公式(7)所定义的拉普拉斯算子;u为顶点纹理坐标构成的矩阵,其大小为|V|×2.为保证纹理坐标的连续性,该拉普拉斯方程的边界条件设置为源网格的融合边界对应目标网格上顶点处的纹理坐标值.因此,该方程的系数矩阵与约束顶点均与公式(2)与公式(7)一致,从而无需重新构造、分解该系数矩阵,可利用前述拉普拉斯矩阵的分解结果,仅需两次回代计算,便可得到纹理坐标.

3.3 融合边界的网格处理

利用泊松融合框架对两个模型进行融合,其前提是融合边界的网格顶点存在一一对应关系,且融合后模型的拓扑是二维流形.文献[9]给出了3种对应策略:投影法、参数化法与稀疏对应与插值法,并且指出第3种方法最为有效.但这种对应方法将使融合边界区域的网格质量变差,可能为后续的几何处理带来数值问题.为此,本文基于第3种方法的思想建立边界顶点对应关系,并给出了一种基于平面Delaunay三角化与离散极小曲面的网格优化方法,以改善融合边界处的网格质量.

3.3.1 融合边界顶点的对应

源网格与目标网格的融合边界均为一个封闭的空间曲线.为建立两个边界的对应关系,需由用户指定几个稀疏的对应顶点(这是本算法唯一需要用户交互的环节);并对每相邻两个指定顶点之间的曲线段,利用弦长参数化方法建立对应关系.具体地,

· 首先,将两个曲线段弦长参数化到单位长度线段上;

· 然后,分别对其中一条线段的每一个顶点,根据等距关系在另一条线段上找到对应点:若该顶点靠近该线段上已有的顶点,则将该顶点作为对应点;否则,对该点所在的边进行细分,将所生成的顶点作为对应点.

图1示意了该算法的思想,其中,S与T分别表示源网格与目标网格边界对应的单位长度参数域,实线分别表示边界,虚线表示对应关系,实心方框表示原边界上的顶点,空心方框表示插入的顶点.

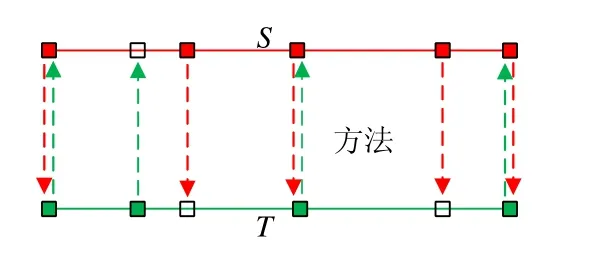
Fig.1 Illustration of the correspondence of merging boundary vertices图1 融合边界网格顶点对应关系示意图

3.3.2 融合边界区域网格的优化

上述对应方法易使网格融合边界区域产生狭长或接近退化的三角形(如图2(a)所示),可能对后续的几何处理带来数值问题.为此,本文在进行网格融合后,对该区域进行局部网格优化.

Fig.2 Comparison of the mesh before and after local mesh optimization图2 融合边界区域局部网格优化前后对比

为使融合边界处的网格既能得到网格质量的优化,又尽可能少地改变原两个网格的几何与拓扑,限定其优化区域为发生拓扑变化的连通区域,亦即融合边界顶点的1-环邻域三角形所构成的带状区域.为此,问题转化成带边界约束的网格优化.现成的网格优化的工具很多,例如经典的各项同性重网格化[34],但该方法对于狭长区域易产生自交.为此,本文给出了一种鲁棒的局部网格优化算法.其思想是:利用带状区域类柱形拓扑特性,沿着连接柱形边界的网格边将其剪开成与拓扑盘同胚的开曲面,并利用弦长参数化方法将该曲面的边界映射到一个平面矩形;然后,运用成熟的带约束Delaunay三角化算法(借助Triangle库[35])对该区域进行三角剖分(如图2(b)所示),该算法根据边界顶点的密度自适应地插入适当数量的顶点并进行三角化;最后,在原融合网格的边界约束下,由拉普拉斯方程构造极小曲面(如图2(c)所示):

其中,Δ为拉普拉斯矩阵;X为待求网格顶点的三维坐标构成的矩阵,其大小为|V|×3.

在离散化求解公式(9)时,本文不采用几何敏感的余切拉普拉斯,而使用拓扑拉普拉斯,即,将公式(3)中的权重设置为均一权重.由于拓扑拉普拉斯与模型的几何无关,这将带来两项益处:不仅能更大程度上减少发生自交的概率,而且能使网格分布更趋于各项同性,从而提高网格质量.由于公式(9)所构造的拉普拉斯矩阵仅针对狭长的局部区域,其规模较小,因此可快速求得结果.

为使所构造的矩形区域的形状和大小尽可能接近原网格区域,本文采用保面积的思想,分别取该矩形的宽w和高h如下:

其中,ls,lt分别是源网格与目标网格融合边界的长度,A为带状区域的面积,即区域内所有三角形面积之和.图2为一个花瓶模型的融合边界处进行局部网格优化前后的对比结果.图2(a)为优化前的网格,图2(b)为将网格边界参数化到一个矩形区域并进行约束Delaunay三角化得到的平面网格,图2(c)为优化后的网格.经过本文算法优化不仅改善了局部区域的网格质量,网格顶点密度分布自然,而且还起到一定的光顺作用.

图3是图2所示例子的完整结果图,其中,图3(a)为源网格(下边界线)与目标网格(上边界线),图中所示为其实际朝向与大小(下同);图 3(b)与图 3(c)分别为经过与未经局部网格优化的融合结果,其网格规模为1051/2070/54/84,3209/6359/27/84,分别表示源网格与目标网格的顶点数、面片数、边界对应前的边界顶点数与边界对应后的边界顶点数(下同).可见:经过网格优化后,网格单元的质量得到了显著改善,并且融合边界处曲面过渡更为自然.

Fig.3 Results of the vase model 1 before and after merging图3 花瓶1模型融合前后的结果

融合边界处经过网格优化后,该区域的纹理坐标随之失效.为快速恢复其纹理坐标,本文利用第3.2节所述方法建立调和映射.由于建立调和映射的网格域拓扑未发生变化,其矩阵结构与公式(9)相同,因此可对该式的拉普拉斯算子进行复用,即省却了矩阵的结构分解步骤,而仅对其进行数值分解与回代计算即可.

4 实验与讨论

本文算法在硬件环境为Inter(R) 4 Core(TM)i5-4590 3.30GHz CPU以及8G内存的PC机,软件环境为Windows 7操作系统,开发工具为Visual C++2017,矩阵相关运算采用Eigen库[36],其中,算法涉及的所有线性方程组的求解均采用其提供的Cholesky分解接口:Eigen::SimplicalLLT〈〉.

为考察融合边界对结果的影响,本文对鲸鱼模型进行切割、扰动后再进行融合,得到图4结果.

· 图4(a)上图为原鲸鱼模型;

· 图4(b)上图为分割后的模型,将头部和尾部分别作为源网格与目标网格,其规模为6949/13824/72/72,3177/6280/72/72;

· 图4(b)下图为扰动后的模型,即:对源网格施加旋转缩放变换后,并对源网格和目标网格的边界顶点沿着切向进行随机干扰,扰动公式为v=v0+t⋅rand(−1,1)e/5.其中:v0为原顶点坐标;t为该顶点单位切向;e为网格边平均长度;rand(−1,1)为随机函数,生成[−1,1]之间的随机数;

· 图4(a)下图为经本文算法融合后得到的结果.由图可见:本文算法能自动调整模型的尺寸与方向,且对融合边界形状敏感度较小,不仅能较好地保持原模型形状,而且在融合边界处保持一定的光滑度.

Fig.4 Merging result for a model with boundary perturbation图4 对模型进行切割扰动后再进行融合的结果

本文算法能够适用于边界顶点密度、形状差异较大模型的融合.本文将图3的目标网格作为源网格,与一个具有方形边界且网格密度较大的目标网格(规模为18953/37720/184/240)进行融合,并得到图5(b)的结果.由结果可见:虽然两者在尺寸、密度和形状上具有很大差异,但本文算法能够自适应计算源网格的尺寸场,使之与目标网格相吻合,并且其融合结果依然较好地保持原模型的整体形状.

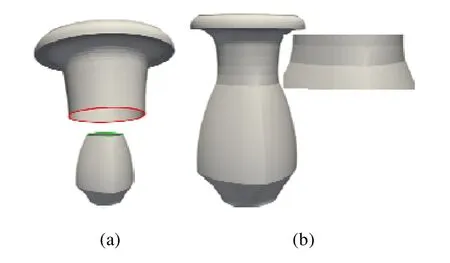
Fig.5 Merging result of vase model 2图5 花瓶2的融合结果

本文算法能够对具有复杂拓扑的模型进行融合.图6分别给出了一个带柄环与一个带两个边界的源网格的融合例子.图6(a)将带椭圆形边界与柄环的模型作为源网格(规模为1638/3716/102/131),把图3中带圆形边界的源网格作为目标网格进行融合,得到图6(b)的结果.由图可见:其融合边界处形状过渡自然,由于边界形状由圆形变为椭圆,其重建网格也被适当拉伸,但其整体形状亦然保持较好.图6(c)将带双边界的模型与一个平面网格(规模为958/1782/134/237,1845/3394/106/237)进行融合,得到图6(d)的结果.与单个边界类似,该情况将狄利克雷边界条件施加在所有边界的顶点上进行求解.图中可见:本文算法能实现多边界的融合效果,虽然边界差异巨大,导致重建模型的边界处形变拉伸很大,但其整体形状获得了一定程度的保持.

Fig.6 Merging results for models with handles and multi-boundaries图6 带柄环与多边界的模型融合

本文算法用较小的时间代价实现了旋转场与尺度场的插值,但其融合结果能与传统的基于测地线的泊松方法相媲美.图7给出了将男人上半身融合到马身的例子(图7(a)为源网格与目标网格,图7(b)为本文算法得到的结果,图7(c)为基于测地线的算法得到的结果,图7(d)为将图7(b)模型(人身)和图7(c)模型(马身)置于同一坐标系下的结果,网格规模为24997/49960/32/105,15654/31227/79/105).由图可见:在视觉上,两种方法得到的结果虽然在大小和朝向上存在一定的差异,但是其形状均能被较好地保持.

Fig.7 Comparison results of our method and geodesic-based Poisson method[9]图7 本文方法与传统泊松融合方法[9]的比较结果

与基于中值坐标的融合方法[4,11]比较,本文方法更为灵活、融合效果更好.本文将小孩头模型作为源网格(规模为28513/56905/81/119),把图7中的人身作为目标网格(图8(a)),分别采用本文方法与基于中值坐标的方法进行融合,得到的结果如图8(b)、图8(c)所示,其运行时间分别为225ms与127ms.虽然后者比本文方法快近一倍,但是本文方法能够根据边界差异自动调整源网格尺寸,而后者无法实现;并且本文方法在融合边界处几何过渡更为自然,效果更好.

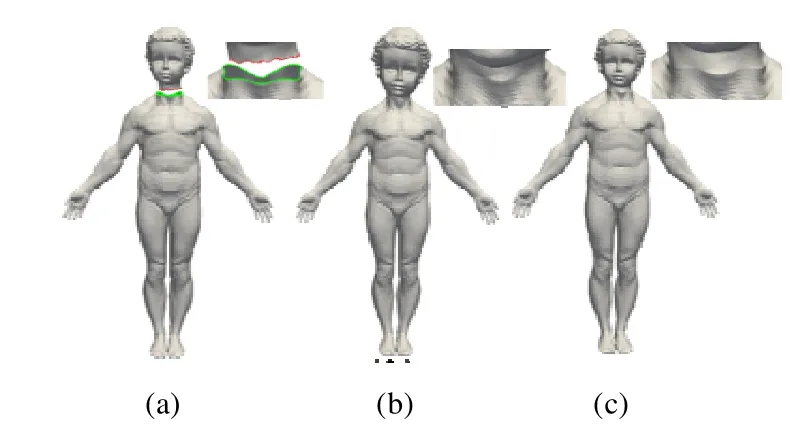
Fig.8 Comparison results with our method and MVC-based method[11]图8 本文方法与基于中值坐标融合方法的比较结果

本文提出的局部网格优化方法能够适应顶点密度差异较大的边界约束.如图9所示(图9(a)为源网格与目标网格;图9(b)与图9(d)为融合结果的不同渲染效果;图9(c)为局部网格放大图,其中,上下两图分别为经过网格优化前后的结果.网格规模为8003/15886/118/134,4285/8668/17/134).将网格密度较大的兔子耳朵与密度较小的牛头进行融合(如图9(a)所示),得到结果图9(b)～图9(d).从图9(c)的局部网格放大图可见:经过本文算法的优化,网格质量得到了明显改善,且顶点密度的分布能从高密度向低密度区域平缓过渡.该特点得益于Triangle[35]强大的三角化功能.

Fig.9 Result of merging rabbit ears with cattle model图9 兔耳与牛的融合结果

我们在各种不同模型上进行了大量测试,发现本文算法均能较好地实现高效融合.图10给出了更多融合的例子(图10(a)飞机(1829/3616/40/68,4515/8806/30/68),图10(b)狗(803/1552/52/77,7983/15884/26/77),图10(c)骆驼(11373/22695/56/91,3408/6773/41/91),图10(d)龙(21595/43030/158/191,15138/30153/121/191)).这些例子均进一步验证了本文算法所具有的上述优点.

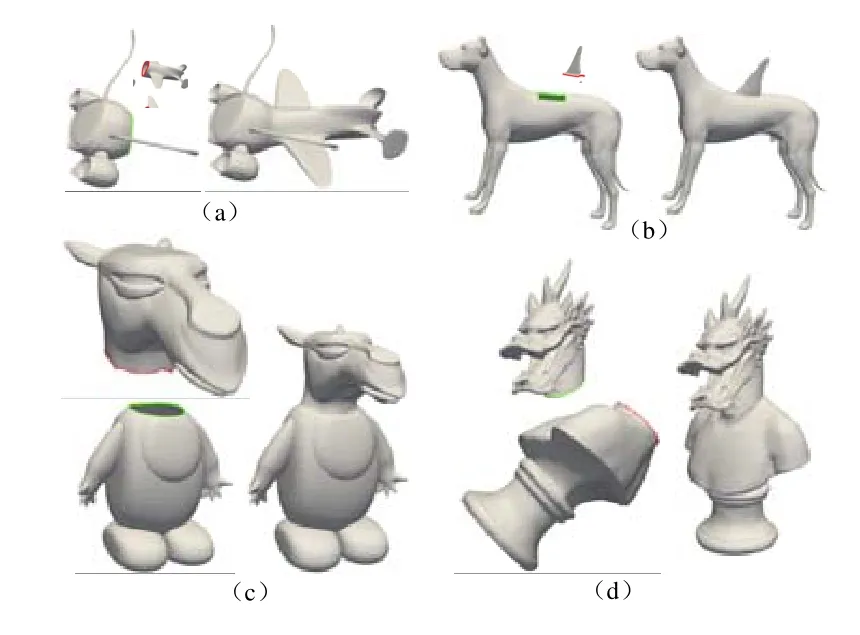
Fig.10 More merging results of various models图10 其他模型的融合结果

为定量地比较本算法与基于测地线的泊松融合算法的重建误差,借鉴网格参数化中形变误差的度量方法,本文采用了共形(角度)形变误差[37]进行度量.即:将原网格与重建网格的每个三角形平摊到平面,并计算平摊后原网格三角形到重建网格三角形之间的仿射变换的两个奇异值σ1和σ2,则该变换的共形形变误差可表示为σ1/σ2+σ2/σ1.基于该形变误差度量,本文比较了两种算法的3种度量误差.

表1列出了本实验所用例子的3种误差比较结果.其中,第2列～第4列斜杠前与斜杠后的数据分别表示本文算法与基于测地线算法[9]的3种形变误差,即最大误差、最小误差与平均误差.由表可见,本文算法与传统泊松融合算法形变误差非常接近,且在多数情况下,本文算法得到的结果具有更小的形变误差.

此外,为展示本文纹理坐标融合算法的结果,本文在图11中给出了未经局部网格优化与经过局部网格优化后的融合结果(图11(a)为源网格与目标网格,图11(b)与图11(d)分别为未经网格优化的融合模型及其纹理图,图11(c)与图11(e)分别为经过网格优化后的融合模型及其纹理图,网格规模为3233/6400/41/107,19826/38492/63/107).由图中汽车外壳的融合边缘处可见:本文虽然在其边界处仅考虑了零阶连续性(狄利克雷)条件,但其纹理坐标的尺寸和方向过渡自然,犹如施加了一阶连续性条件(图12亦然).这一现象表明,在纹理空间“挖洞”并进行保持位置约束的“填充”后,尽管其填充曲面形状发生了变化,但是其纹理的方向依然能获得较好的保持.同时,本文在进行局部网格优化后更新了纹理坐标,其结果与未更新前几乎没有差异(如图11(d)和图11(e)).该现象一方面体现了余切拉普拉斯几何敏感的特性(与网格无关),另一方面也说明了本文纹理坐标融合方法的有效性.

另一方面,为考察纹理融合算法的鲁棒性,本文将具有不同形状、不同融合边界的鼻子“嫁接”到带纹理坐标的人脸模型上,得到图12所示的融合结果(图12(a)为目标网格,图12(b)～图12(d)为不同形状的源网格,图12(e)～图12(g)为对应的纹理融合结果).由图可见,本文算法能同时较好地实现几何融合与纹理坐标融合,合成模型的几何与纹理坐标均能在融合边界处光滑过渡,并较好地保持源网格的形状.

比起传统的基于测地线的泊松融合算法,本文算法不仅能够获得相似的融合结果,而且在效率上有显著的提升.本文将算法分为3个部分:边界对应、几何重建与网格优化,分别测试了各个部分的运行时间.其中,几何重建中,旋转场与尺度场的插值是原算法最为耗时的环节,本文分别比较了两者所耗时间.在比较实验中,本文采用了基于热核的高效测地线算法[38].表2列出了上述实验例子的运行时间,其中,R/S场表示旋转场与尺度场的计算,第3列、第4列斜杠前与斜杠后的数据分别表示本文算法与基于测地线算法[9]所耗时间.由表中可见,本文算法在边界对应与网格优化均耗费较少的时间.这是由于算法处理的是局部网格,计算代价较小.从表中第3列和第4列的比较结果可看出:本文的算法在计算旋转与尺度场时仅需若干毫秒甚至低于1ms,比起基于测地线的算法快2个数量级以上;相应地,其几何重建部分得到了较大的加速.因此,本文算法使泊松融合的交互应用成为现实.

Table 2 Running time of the two merging algorithms on different models (ms)表2 两种融合算法在不同模型上的运行时间 (毫秒)

5 总结与展望

本文利用拉普拉斯算子的优良性质,将网格融合中几何、旋转场、尺度场、纹理坐标的计算统一运用该算子进行建模,使之在计算中得到多次复用,从而提高了计算效率.比起传统的泊松融合方法,本文方法不仅能获得相媲美的实验结果,能够实现纹理坐标的快速融合,而且在效率上大为提升,达到交互响应速度.此外,本文提出了针对融合算法的鲁棒高效的局部网格优化方法,能够有效地改善融合边界区域的网格质量,可为高质量组装式建模应用提供高效方法[39].

本文提出的纹理坐标融合方法采用了单片全局参数化,对于融合边界有割缝或者源模型具有复杂拓扑的情形便不再适用.今后,我们将考虑基于多片全局参数化的纹理融合,引入切割线处理复杂拓扑,并在切割线处考虑连续性约束,以拓展该算法的应用范围.由于多片全局参数化最终亦可转化为泊松方程,因此我们将研究如何在该情况下复用拉普拉斯矩阵以提高效率.同时,我们也将考虑定义在网格上的其他标量场的融合问题.

致谢本文实验所用的部分模型来自模型库AIM@Shape以及国防科技大学徐凯博士的个人主页(http://kevinkaixu.net/projects/civil.html),在此表示感谢.