基于滑模控制的Sigma-Delta调制器参数设计和优化

(1.北京化工大学 信息科学与技术学院，北京 100029; 2.北京化工大学 软物质科学与工程高精尖创新中心，北京 100029)

随着数字电路功能越来越强大，其对模数转换器性能的要求也越来越高，传统的模数转换器的转换精度一般都不高，不能够满足系统高精度要求。Sigma-Delta调制器是过采样模数转换器的一种，属于高精度高稳定性模数转换器，同时对前端抗混叠滤波器性能要求较低[1-4]。利用过采样技术和噪声整形来增加有效分辨率和消除系统高频噪声的Sigma-Delta ADC广泛运用于数字音频、MEMS传感器、汽车电子、综合业务数字网等领域[5-8]。Sigma-Delta调制器是通过过采样来提高系统的信噪比；通过噪声整形来降低信号带内的量化噪声功率[9]。该调制器的实质是利用高速度换取高精度，从而降低实现高精度模数转换器的复杂性。

Sigma-Delta调制器按系统的等效积分器个数可以分为二阶系统和高阶系统[10]。二阶系统全时稳定，且系统结构简单、电路容易实现，系统中仅包含敏感结构和量化器等电路，不包含电学积分器，但由于阶数较低，限制了Sigma-Delta调制器的噪声整形能力，造成系统整体的性能不高。高阶Sigma-Delta调制器在具有低通滤波特性的敏感结构后面级联积分器，积分器的个数越多、阶次越高，噪声整形能力越强，整体性能也就越高，但是高阶Sigma-Delta调制器系统存在稳定性差、系统参数设计复杂、系统的动态范围较窄的缺点[11]。目前，多采用级联结构，该结构能够保证系统的高稳定性，但是产生了新的器件匹配问题，加大了设计难度。高阶一位Sigma-Delta 调制器能以相对简单的电路和适中的过采样频率得到较高的转换精度和线性度，因此在数字电路领域得到了广泛应用。但是高阶一位Sigma-Delta 调制器除了面临系统稳定性问题外，其非线性也增加了系统的设计和分析难度。

本文将滑模控制理论[12]引入到高阶一位Sigma-Delta 调制器系统中，对调制器系统的工作原理进行重新解释，消除了一位比较器非线性对系统的影响，从而得到线性高阶一位Sigma-Delta调制器。在此基础上，采用粒子群优化算法对线性高阶一位Sigma-Delta调制器参数进行优化设计，在简化设计难度的同时为获得高信噪比高稳定性的Sigma-Delta调制器提供了可能。下面将对本文所提方法进行详细讨论。

1 高阶一位Sigma-Delta调制器系统非线性分析

1.1 高阶一位Sigma-Delta调制器数学模型

所采用的高阶一位Sigma-Delta调制器系统结构如图1所示。

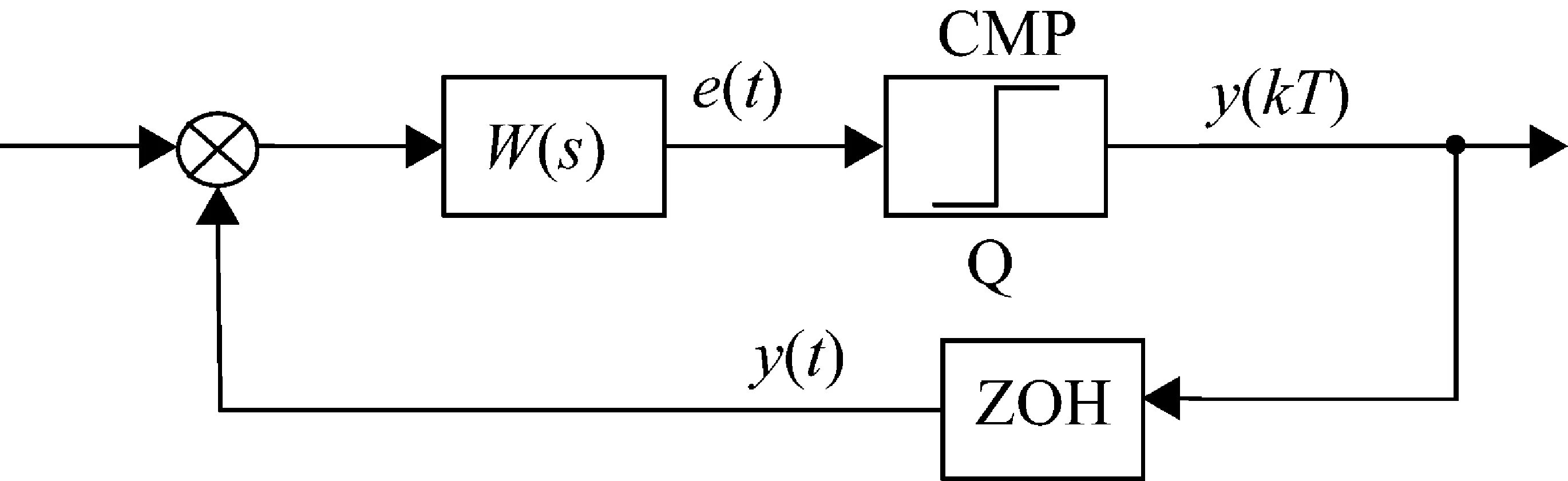
图1 高阶一位Sigma-Delta调制器系统框图

图1中，CMP为一位比较器，W(s)为Sigma-Delta调制器系统积分器，其表达式为

(1)

其中，

N(s)=η(sn-1+β1sn-2+β2sn-3+…+βn-1)

(2)

D(s)=sn+α1sn-1+α2sn-2+α3sn-3+…+αn

(3)

式中，n为积分器阶次；η为积分器增益，η>0；α1,α2,…,αn为积分器的分母系数；β1,β2,…,βn-1为积分器的分子系数。

假设，式(1)中没有零极点相消，积分器传递函数W(s)可写成式(4)所描述的状态空间表达式：

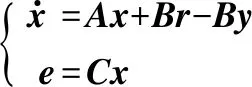
(4)

式(4)对应的状态空间原理图如图2所示。

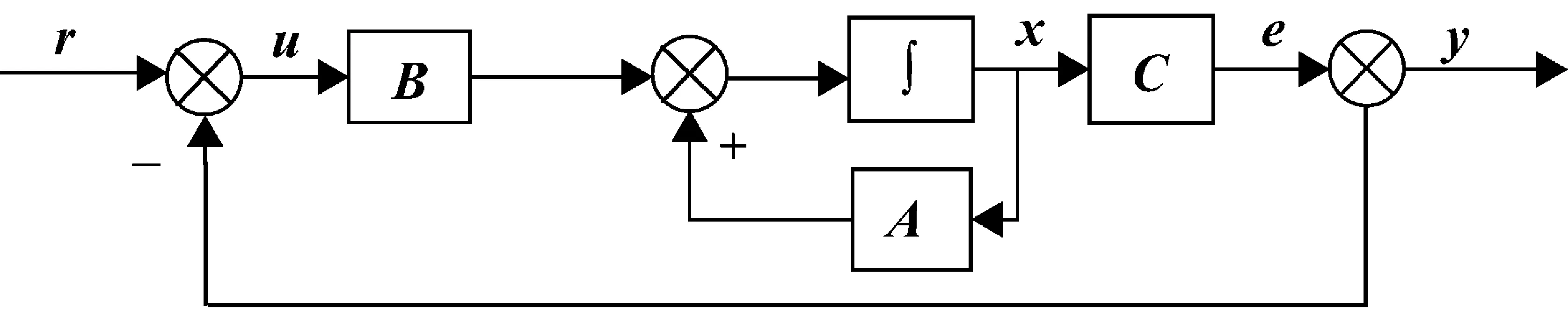
图2 高阶一位Sigma-Delta调制器状态空间原理图

图2中，x为n维向量；A、B、C为系统矩阵,其与积分器传递函数W(s)有如下关系:

W(s)=C(sI-A)-1B

(5)

1.2 高阶一位Sigma-Delta调制器滑模面设计

如图1所示，针对Sigma-Delta调制器系统，设计滑模面的思路是在每一个采样瞬间保证W(s)的输出趋于零，即一位比较器的输入趋于零。如果系统的采样频率无限大，则滑模趋近率是连续的，即可以保证e=0，那么W(s)的状态x可以一直在滑模面e=Cx=0上运动。然而，系统的采样频率不可能无限大，因此不可能保证e=0，所以W(s)的状态x不可能在滑模面e=Cx=0上运动。这种情况下，选取滑模区域|e|<ε，那么W(s)的状态x将在滑模区域|e|<ε上运动。

基于Sigma-Delta调制器系统，设计滑模面并且能够保证系统状态在滑模面上稳定，需具备以下两个条件：

① |u|<1，同时u=(CB)-1CAx+r;

②N(s)为最小相位系统。

只有满足上述两个条件，同时滑模面应满足|e|<2ητ，其中η为传递函数W(s)的增益、τ为系统的采样时间，才能保证Sigma-Delta调制器系统能够稳定地处于滑模运动。由图1可得，系统误差可以表示为

E(s)=W(s)·(R(s)-Y(s))

(6)

式中，Y(s)、R(s)和E(s)分别为y(t)、r(t)和e(t)的拉氏变换。

在系统稳定情况下，通过式(6)可得：

Y(s)=R(s)-W-1(s)E(s)

(7)

若式(7)稳定且满足零初始条件，那么对式(7)进行拉氏反变换，同时结合条件①和条件②可得系统输入需满足式(8)才能保证系统是稳定的，即

|r(t)|<1-2τ‖G(s)‖1

(8)

式中，‖G(s)‖1表示传递函数G(s)的L1范数。对式(8)进行拉氏反变换，同时结合稳定条件①和条件②可得

(9)

又由式(4)可得：

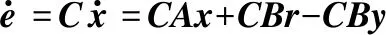
(10)

通过式(10)可导出y：

(11)

将式(11)代入到式(4)中可得：

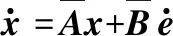
(12)

式中，

(13)

由式(13)和条件①可得：

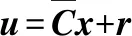
(14)

其中

(15)

对式(14)进行拉氏变换可得：

U(s)=R(s)+η-1G(s)E(s)

(16)

式中，

(17)

通过式(17)可以推导出：

‖u‖∞≤‖r‖∞+η-1‖G(s)‖1‖e‖∞

(18)

又由式(18)可得：

|r∞+η-1|G(s)1|e∞≤1

(19)

因为|e|<2ητ，所以有

‖r‖∞≤1-2τ|G(s)1

(20)

不等式(20)给出了系统输入的稳定范围，若W(s)=η/s，那么G(s)为零，则通过式(20)可得，不管采样频率多大，都不会影响系统的稳定性。这里可以为G(∞)选取最大输入幅值‖r‖∞，因为G(∞)≈β1-α1，那么

‖r‖∞≈1-2(β1-α1)τ

(21)

式(21)可以为积分器参数的设计提供选取规则，即当Sigma-Delta调制器输入和采样时间确定的情况下,若积分器系数满足式(21)可以保证积分器的输出(一位比较器的输入趋于零)，从而消除一位比较器非线性对整个系统的影响。

2 高阶一位Sigma-Delta调制器参数优化

2.1 五阶积分器W(s)传递函数

采用五阶一位Sigma-Delta调制器为研究对象，即W(s)的表达式为

(22)

选取Sigma-Delta调制器的最大输入为0.1g(g=9.8 N/s2)，采样频率为128 kHz，代入到式(21)中可以得到:

β1-α1=1280

(23)

将式(23)代入到式(22)得：

(24)

下面将对积分器W(s)系数进行优化设计，即对式(24)中系数采用粒子群优化算法进行优化整定。

2.2 粒子群优化算法

Kennedy和Eberhart于1995年基于对鸟群运行模式的简化研究及行为模拟开发了一种优化算法——粒子群优化算法[13](Particle Swarm Optimization，PSO)。设在一个D维的搜索空间里存在n个粒子，这时每个粒子代表以一定速度飞行的一只鸟。对于要求解的优化问题，此时的一个粒子就是一个潜在的解。每个粒子都具备以下信息：目前为止自己发现的最优位置(pbest)，并以pbest作为自身飞行的经验、到目前为止整个群体所找到的最优位置(gbest)，该值为pbest中的最优值。在整个寻优过程中，每个粒子的适应度取决于所采用的优化函数的值。粒子群优化算法是一种迭代优化算法，即每个粒子通过若干次迭代搜索，最终找到最优解。在每次的迭代过程中，微粒通过追踪pbest与gbest的位置来更新自己。粒子群优化算法在寻优过程中，运用以下公式来更新自身的速度与位置：

vk+1=ωvk+r1(pbestk-vk)+r2(gbestk-vk)

(25)

xk+1=xk+vk+1

(26)

式中，vk为粒子的当前速度;xk为粒子的当前位置；ω为惯性权重；r1,r2称为加速常数，分别用来表示pbestk、gbestk对每个粒子的影响强度，一般r1,r2∈[0,2]。

2.3 积分器W(s)参数优化过程

积分器W(s)参数优化过程如下。

(1) 初始化粒子群参数。待优化参数为α5,α4,α3,α2,α1,β4,β3,β2,η，则可将粒子群优化算法的位置矢量选取为xi=[α5,α4,α3,α2,α1,β4,β3,β2,η]，同时选定粒子个数为1000，最大迭代次数取100，ω=0.9,c1=c2=2。

② 目标函数选定。在Sigma-Delta调制器系统中，信噪比(SNR)是验证系统性能的主要参数，若调制器信噪比低，则Sigma-Delta调制器的精度、分辨率以及抗干扰能力就很难满足实际应用要求。因此，选取SNR为粒子群优化算法的目标函数，通过优化积分器传递函数W(s)参数，在优化空间内求取最大SNR。SNR的计算通过Sigma-Delta调制器输出的功率谱密度(PSD)求取，在每一次优化迭代过程中将优化参数代入到所搭建的Sigma-Delta调制器Simulink系统模型中(如图3所示)，通过Matlab工具箱中calcSNR函数计算信噪比。

③ 利用式(25)、式(26)更新粒子的速度与位置，对当前粒子进行性能评价，同时更新pbest、gbest。

④ 若满足寻优终止条件，则停止迭代，否则返回步骤③。

图3给出了所搭建的对应于图1的Sigma-Delta调制器的Simulink仿真图。

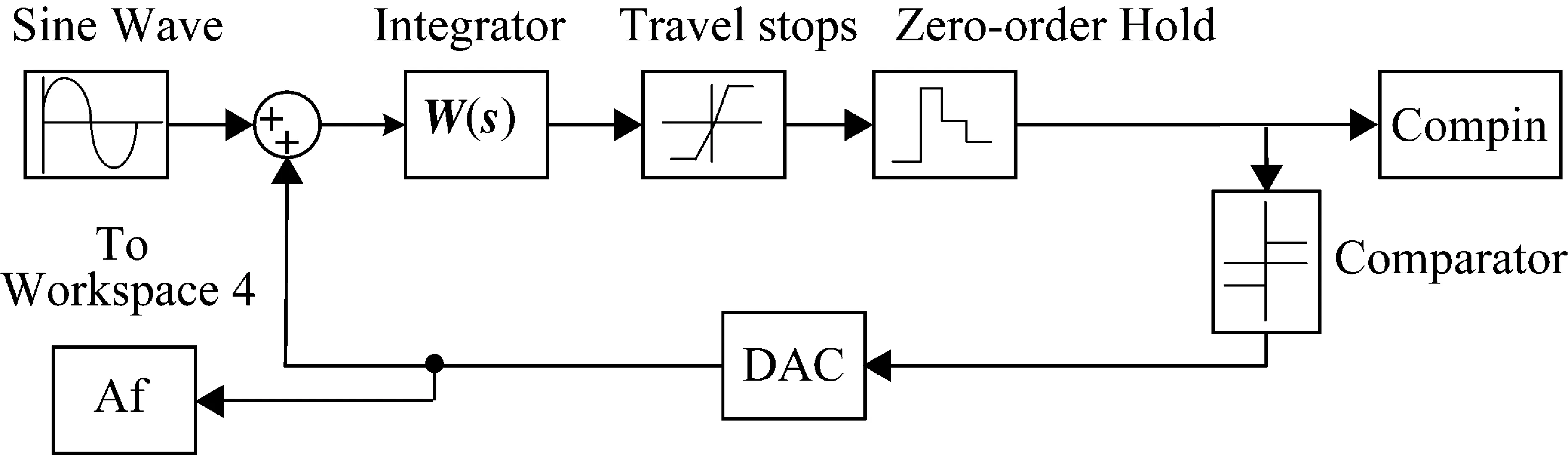
图3 Sigma-Delta调制器Simulink模型

按照上述介绍的参数优化流程编写Matlab程序，本文程序中采样频率设定为128 kHz，过采样倍数为OSR=64。Simulink模型中，输入信号选用频率为45 Hz，幅值为0.1g(g=9.8 N/s2)的正弦波，运行程序将每次优化参数xi=[α5,α4,α3,α2,α1,β4,β3,β2,η]代入到Simulink模型中，同时通过calcSNR求取目标函数。通过100次搜索结果可得所构造的分数阶Sigma-Delta调制器所取得的信噪比在97～126 dB之间，同时在混沌粒子群寻优100次过程中得到的最高信噪比为SNR=125.239 dB，对应的优化参数为α5,α4,α3,α2,α1,β4,β3,β2,η如表1所示。

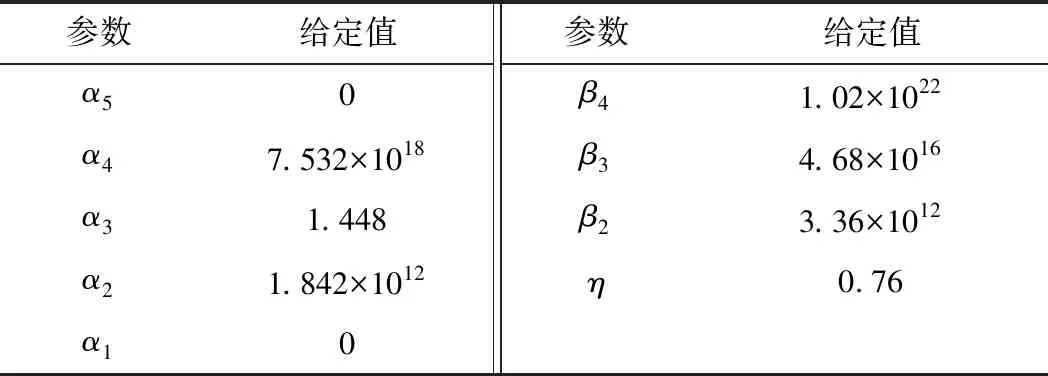
表1 参数优化结果

将表1中的优化参数代入到Simulink模型(如图3所示)中，得到分数阶Sigma-Delta调制器的功率谱密度(PSD)如图4所示。

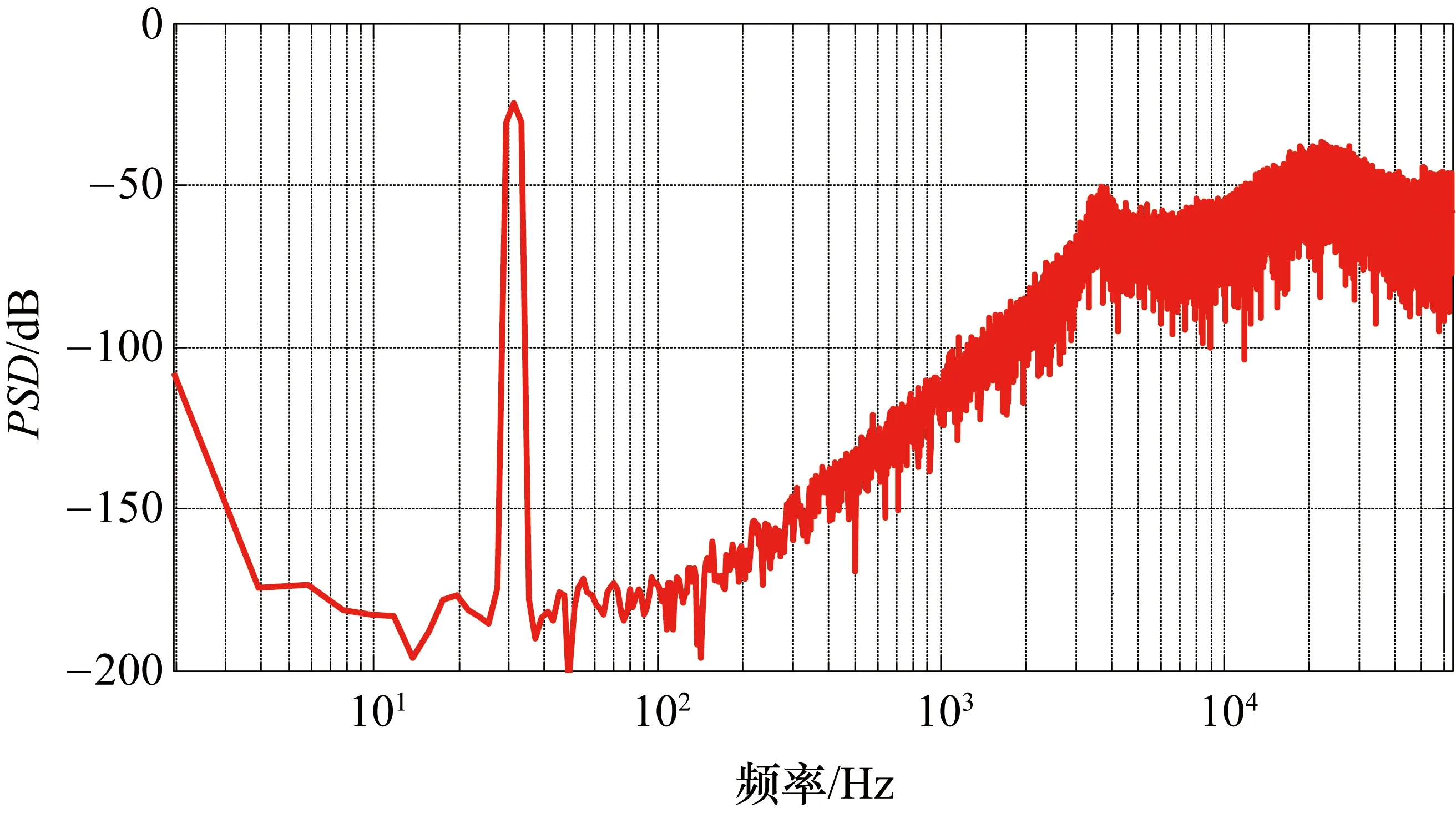
图4 Sigma-Delta调制器的噪声能量谱密度示意图

在图4中，有效信号主要集中在低频段(5～250 Hz)，而噪声主要集中分布在高频段(500 Hz以上)。由图4可得在在5～150 Hz范围内，其输出噪声基底约为-170 dB、信噪比为125.239 dB，因此，可以说所优化的Sigma-Delta调制器具有很好的低频噪声抑制能力。将表1中的优化参数代入到图1,绘制出Sigma-Delta调制器闭环系统的根轨迹如图5所示。

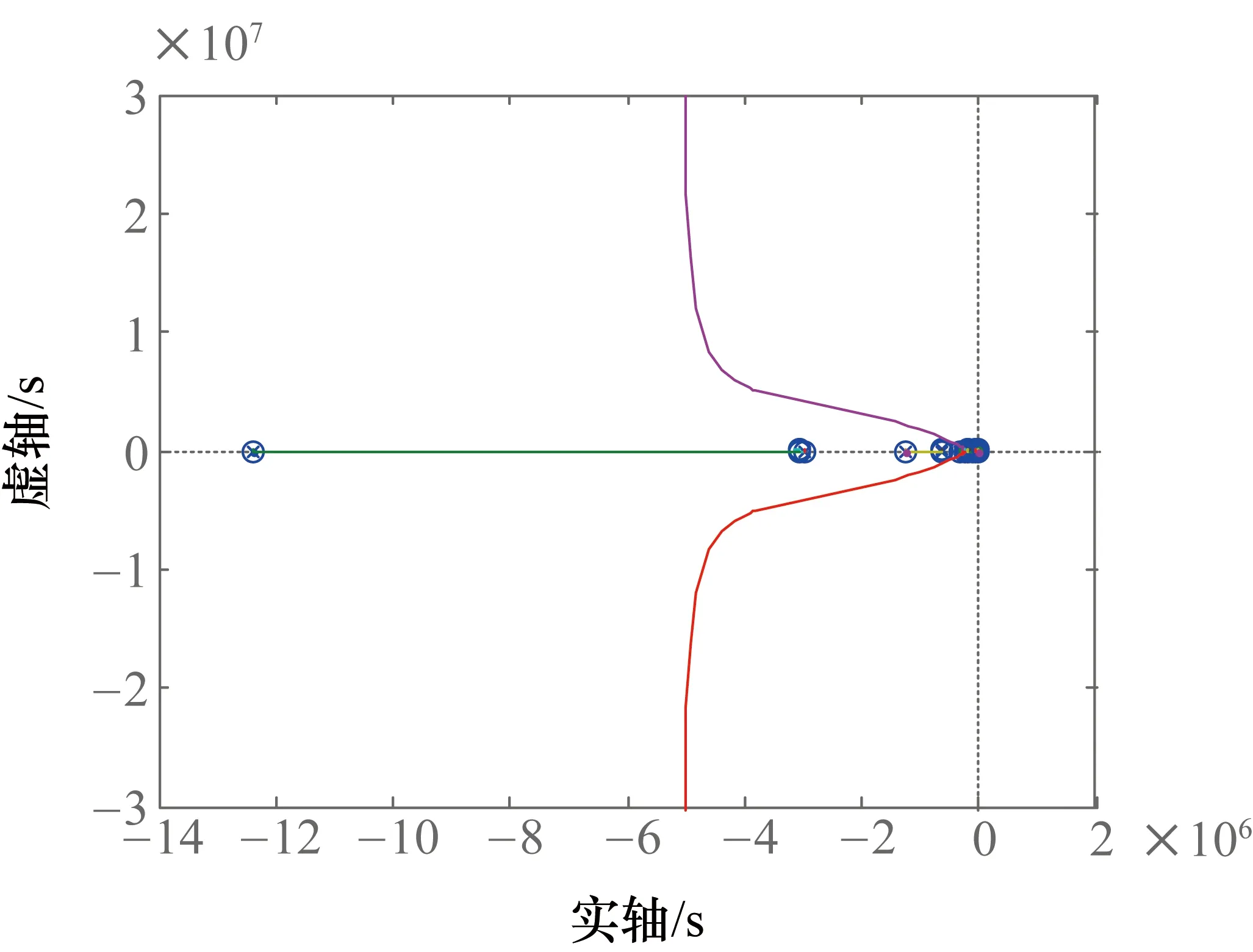
图5 分数阶Sigma-Delta调制器闭环系统根轨迹

从图5中可得，在基于滑模控制理论所设计的Sigma-Delta调制器系统是绝对稳定的，其闭环传递函数的所有根都位于复平面s域的左半平面。

3 结束语

基于滑模控制理论推导出了积分器参数与采样时间以及Sigma-Delta调制器输入的关系，当积分器参数满足所推导关系时，能够消除调制器非线性环节对系统的影响，从而为分析系统提供方便。并采用粒子群优化算法设计积分器参数，简化了传统Sigma-Delta调制器参数设计的难度，通过优化得到了一组参数，其对应的信噪比为125.239 dB。由于系统中不存在非线性影响，因此可以采用根轨迹来分析系统的稳定性。通过根轨迹可以得知，所设计的五阶一位Sigma-Delta调制器系统是稳定的。