改进GA-PSO优化SVM的行人检测算法

2

(1.西南科技大学 信息工程学院， 四川 绵阳 621010；2.特殊环境机器人技术四川省重点实验室，四川 绵阳 621010)

行人检测即判断输入的图像或视频序列中是否出现行人，并确定其位置。它是计算机视觉领域极具挑战性的研究热点，如今在智能辅助驾驶、行人分析和智能视频监控等方面都发挥着很重要的作用。但是因为人体形态的不同、着装的多样化，场景中经常存在光照变化、气候变化以及景物遮挡等因素，行人检测的研究也变成了一门极具挑战性的热门课题。

现在行人检测主要采用基于统计学习的方法，根据大量样本构建行人检测分类器，其性能提升主要与行人特征提取和分类器的训练有关。传统的特征提取方法有Haar、LBP、HOG等，主要分类器有神经网络、SVM和Boosting 等。由于HOG特征在边缘特征提取的优越性，HOG+SVM[1]成为了一种经典的行人检测方法，近年来，学者们一直在对此方法进行改进。针对HOG特征维数较大、提取速度较慢的缺点，提出了利用PCA[2-4]对其进行特征降维处理以及使用GPU[5-6]对其进行加速处理；针对SVM分类器检测识别率不高的缺点，提出了使用多个分类器结合，如：SVM+AdaBoost[7-8]等方法以及多核SVM[9]进行行人检测。多核SVM检测时，由于核参数比较多，将多个核参数共同优化[10-11]，以此来提高检测率。在此基础上，本文使用GA-PSO[12]算法对核函数的参数进行优化，使用优化得到的分类器对PCA-HOG特征进行分类，从而提升准确率和检测效率。

1 本文研究方案

本文在传统方法研究的基础上，利用主成分分析(PCA)对提取的HOG特征向量进行降维处理；利用组合核函数的SVM分类器在检测方面准确率的优势，在前人对优化[13-14]算法研究的基础上，使用改进的GA-PSO算法对核函数的参数进行优化，根据优化结果得到一个最终的分类器，检测方案如图1所示 。

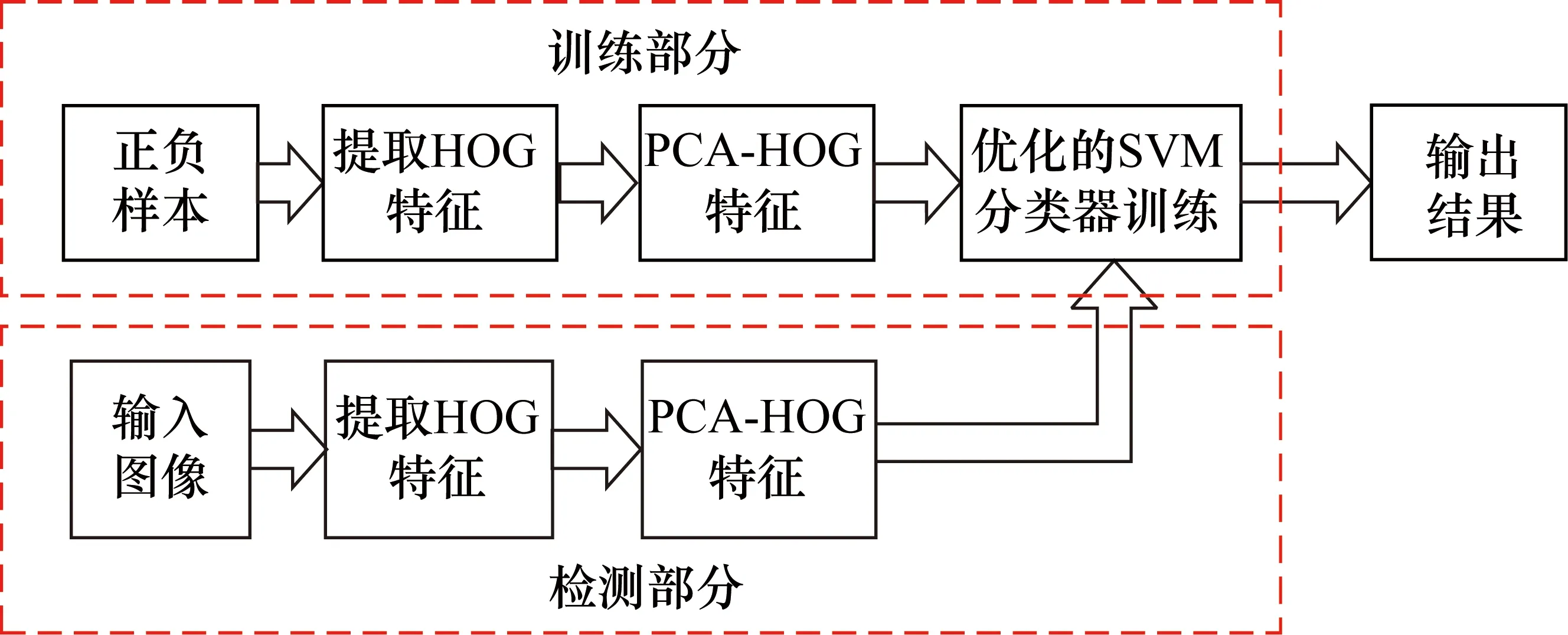
图1 检测方案图

1.1 特征提取

HOG特征即指图像的梯度直方图特征，表征的是图像的局部梯度幅值及方向特征。HOG特征提取的主要步骤如下。

① 图像标准化颜色空间。由于颜色所提供的信息对于特征的提取过程影响不大，首先应当将图像转化为灰度图像，然后进行Gamma矫正，完成颜色空间的标准化以方便后续的工作进行。

② 梯度计算。主要包括方向和大小的梯度信息，Dalal 论文中测试了不同的梯度模版，主要包括一维模版、对角线模版以及Sobel模版。实验证明，[-1,0,1]模版在测试中效果最好。

主要计算过程为

Gx(x,y)=H(x+1,y)-H(x-1,y)

(1)

Gy(x,y)=H(x,y+1)-H(x,y-1)

(2)

梯度大小为

(3)

梯度方向为

(4)

③ 梯度方向直方图。将图像划分成若干个cells，8×8=64个像素为一个cell，相邻的cell之间不重叠。在每个cell内统计梯度方向直方图，将所有梯度方向划分为9个bin(即9维特征向量)。

④ 重叠直方图处归一化。因为图像的光照差异会造成前景背景对比差异，导致梯度幅值的范围很大，因此，归一化对于检测结果就非常必要。

⑤ 收集所有块的HOG特征形成特征向量。

处理过程的效果如图2所示。

图2 HOG特征提取图

PCA进行降维处理是一种常用的数据分析方法，主要通过线性变换将原始数据变换为一组各维度线性无关的表示，实验表明，用PCA对HOG特征降维有很好的效果，在不低于最低分辨识别率的前提下可以将特征向量降到20维，大大提高了检测速度。

1.2 分类器算法

SVM[15]是一种基于统计学习理论的模式识别方法。给定的一组训练样本可以表示为：{xk,yk}，k=1,2,…,N。支持向量机最优分离函数为

(5)

1.2.1 核函数的参数

由于本文的特征维数较大，应该采用核函数将输入空间的数据映射到高维空间去，在高维空间中求得一个最优的分类面，那么就使一些原本不能线性可分的数据在高维空间中得以处理，得到一个最优的分类结果，选择不同的核函数将会有不同的分类效果。

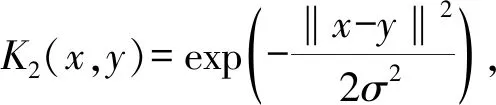
根据高斯核函数和多项式核函数的特点，将两种核函数进行组合，进而得到一个组合核函数[16]：K(x,y)=α1K1(x，y)+α2K2(x,y),α1,α2分别代表多项式核函数和高斯核函数所占比例并且α1+α2=1。由此可知，本文的核函数会有σ,α1,d,C共四个参数，它们会决定函数的特征空间、置信度、经验风险以及全局性和局部性等，需要对各个参数进行同时优化，才能达到一个最优的分类面。

1.2.2 svm核参数优化

(1) GA算法。

遗传算法[17-18]是根据大自然中生物的进化以及基因变异等规律得到的一种参数优化方式，通过对个体的适应度进行评估，将其进行交叉以及变异作用于群体后，得到一个最优解作为输出。遗传算法对于全局最优有很好的效果，并且搜索能力较强，速度较快，但是其操作比较麻烦，面对不同环境要重新进行参数的选择，大多数情况效率较低。

(2) PSO算法。

粒子群算法[19]是根据粒子群的各个粒子飞行过程中以及其他粒子在飞行过程中的经验不断调整飞行位置，得到各个粒子的最优位置，进而得到整个粒子群的最优解。粒子群算法操作简单，方便计算，在很多优化方面都有使用，但是，大多数情况下，它仅可以得到局部最优解。

粒子位置和速度调整公式为

(6)

式中，X为粒子位置；υ为粒子速度；k为迭代次数；pbest为单个粒子位置最优值；jbest为群体位置最优值。

(3) GA-PSO算法。

遗传算法对于全局最优有很好的效果，并且搜索能力较强，速度较快；粒子群算法操作简单，方便计算，在很多优化方面都有使用，但时，大多数情况下，它仅可以得到局部最优解。鉴于GA算法和PSO算法在全局和局部寻优的特点，将两种算法进行融合，形成GA-PSO混合算法。

本文在以下两方面进行优化。

① 鉴于PSO的参数(如λ1、λ2)一般通过经验选择，可能达不到很好的效果，因此用GA算法对其进行优化，提高算法的效率。每一个GA算法的粒子为PSO的加速权值(λ1，λ2)，在此参数优化的条件下，PSO算法对核函数参数(σ,α1,d,C)进行优化，以达到最佳的优化效果。

② 对于PSO 算法的参数ω来说，传统的权重系数ω变化方式为

(7)

式中，t为当前迭代次数；Tmax为最大迭代次数;ωmin为最小权重；ωmax为最大权重。变化方式如图3所示。 但是，在研究中发现，迭代过程中，惯性权重调整通常希望使粒子早期具有较强的全局搜索能力，防止早熟收敛，后期具有较强的局部搜索能力，加快收敛速度。换句话说，在迭代次数t较小时，惯性权重应该随着t的增大缓慢减小，随着迭代次数t变大，惯性权重减小的速度加快，当迭代次数较大时，又缓慢地减小，以便在前期获得快速的收敛速度，并且在后期也具有一定的局部搜索能力。在前人[19]的研究基础上，本文对传统线性变化的ω进行改进，采用二次函数作为ω的变化方式。改进的公式为(变化方式如图4所示)

(8)

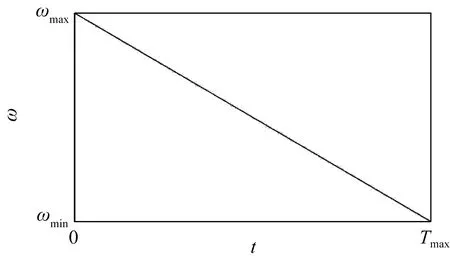
图3 传统ω随迭代次数t变化图

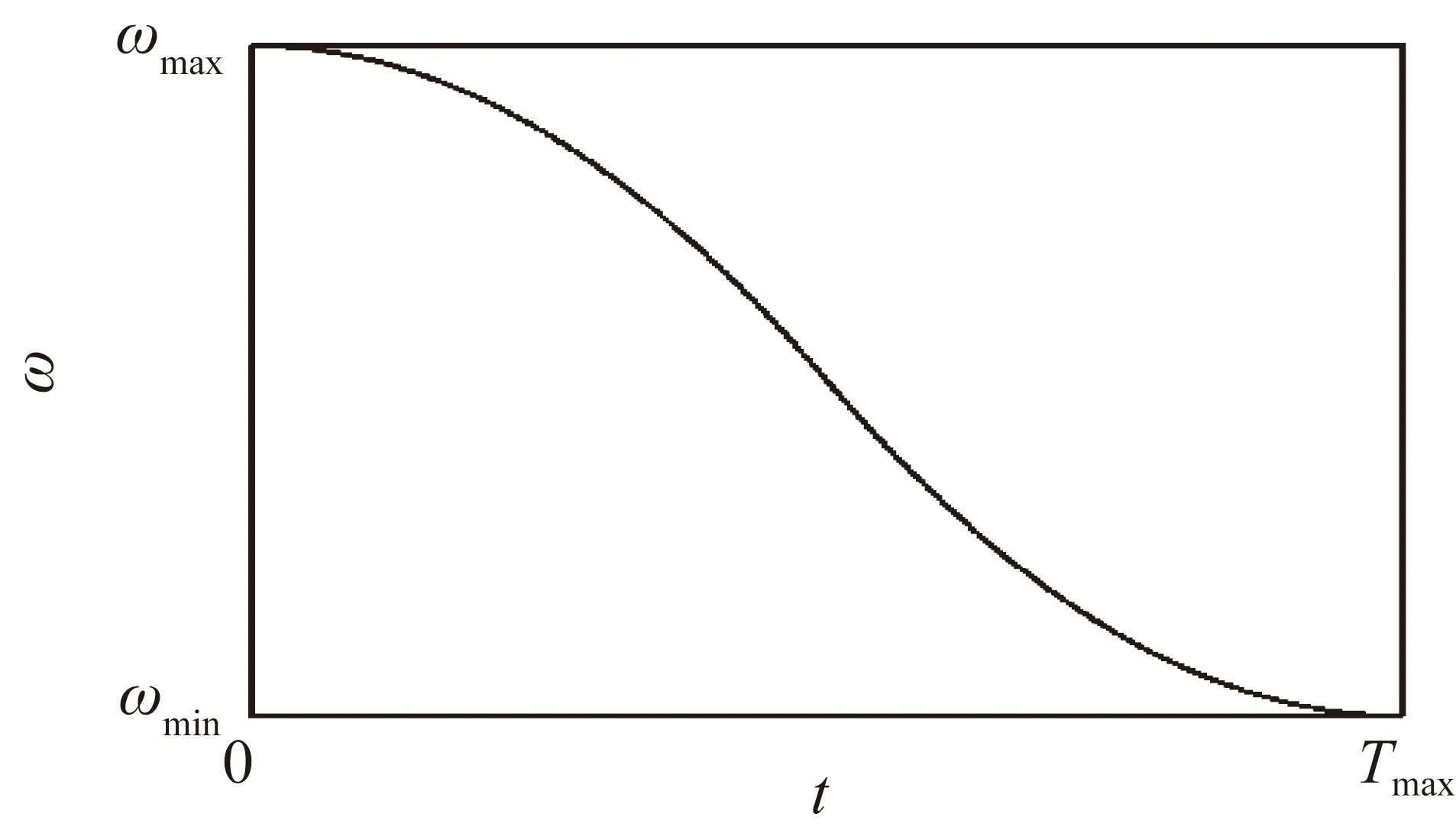
图4 改进的ω随迭代次数t变化图

由图4可知，ωmax在刚开始时变化比较缓慢，此变化方式可以使粒子在前期的全局搜索能力增强，在中期时变化速度加快，可以提高中后期的搜索速度，在后期又逐渐平缓，对局部的搜索也有很好的效果，确保早期全局搜索最优解的能力和后期局部搜索最优解的能力。此方法更满足本文对参数的优化要求。通过前人[20]的经验，发现ωmax的值为0.9、ωmin的值为0.4时，可以满足大部分数据优化的需求。实验证明，它可以提高收敛速度并实现深度和广度的优化，达到很好的优化效果。GA-PSO优化核函数参数的流程图如图5所示。

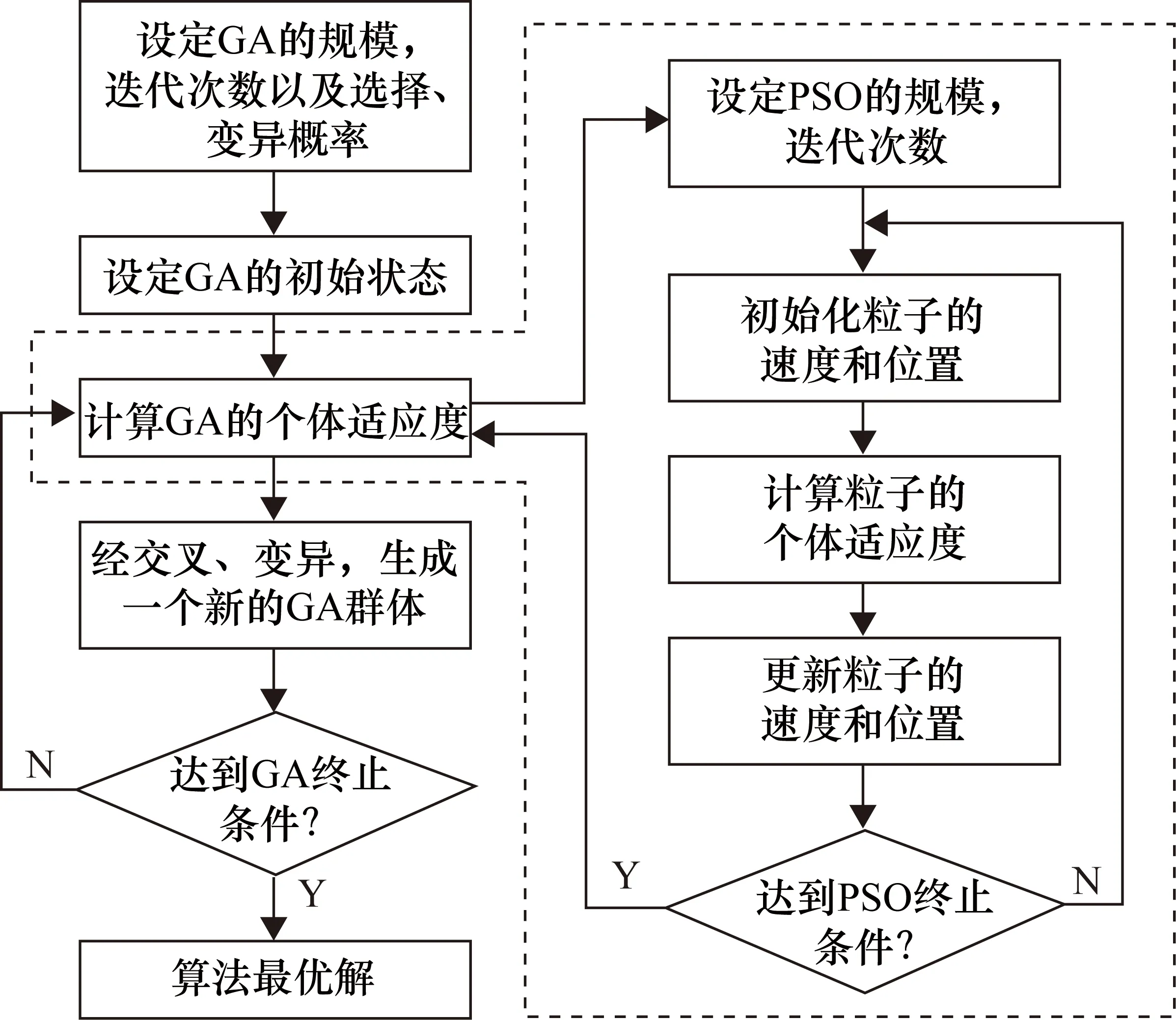
图5 GA-PSO算法流程图

本文算法的具体步骤如下。

(1) 对PSO算法参数λ1、λ2进行二进制编码。GA算法中每一个粒子为(λ1,λ2)，其中(λ1,λ2)∈[0,4]。

(2) 设定GA的初始种群规模和迭代次数，生成一个初始种群。其中种群规模过大，会提高算法的运行时间，过小则会影响分类精度，一般取粒子维度的5～10倍，本文来说种群规模∈[10,20]。

(3) 计算GA算法每个个体的适应值fx，以PSO的最优解为GA算法的适应值。

① 设定PSO迭代次数和种群规模的值，种群规模设置的要求与GA算法相同，本文种群规模∈[20,40]。

② 每个粒子代表一组核参数(σ,α1,d,C)，σ∈[0.1,5]，α1∈[0,1]，d∈[1,10]且d∈N+，C∈[1,1000]。在此参数范围内设置一个最初的位置x0，将其作为最优位置。

③ 设置PSO算法的适应度函数gx。适应度函数为当前核函数参数下的行人检测率，表示为

(9)

式中，R为检测率;ncorrect为样本里被正确分类的行人数目；ntotal为样本总数。

④ 若当前粒子的gx>gpbest，则将X⟹pbest；若gx>gpbest，则X⟹jbest。

⑤ 更新粒子的速度和位置信息。由式(6)可知，经过k代更新后，最终的位置信息由Xk+1达到迭代次数时得到。

⑥ 按式(8)重置ω的值。

⑦ 检查是否达到迭代次数。若是，输出最优值Xk+1；若否，返回至步骤③。

⑧ 最终得到的PSO最优值(最高识别率)即GA算法的适应值。

(4) 由适应值计算GA粒子选择概率，选择概率公式为

(10)

式中，p为选择概率。可知，适应值越大，则被选中的概率就越大。

(5) 选中的粒子进行交叉、变异运算。进行交叉操作时，确定一个交叉概率Pc，运算之初会有一个随机的数，当它小于Pc时，就进行交叉运算。变异操作与交叉操作相似。

(6) 经过交叉、变异运算后会得到一个新的种群，即为此次GA运算的最优解。若未达到迭代次数，返回至步骤(3)；否则输出最优解。

(7) 得到最优的一组核参数(σ,α,d,C)。

2 实验结果与分析

为验证本文算法，在Visual 2013+OpenCV 2.4.13的环境下进行本次实验，训练样本为64×128的图片，其中，正样本数目为1200张，负样本为2400张，测试样本为500张行人图片，主要来自IN-RIA数据库、MIT数据库以及自己拍摄的图片，主要包括城市、雾天、晴天等不同场景。

由于采用组合核函数作为最优的核函数进性分类，其中主要涉及σ,α1,d,C这4个参数，对其进行同时优化，通过本文改进的GA-PSO算法进行计算，并与其他3种不同的优化方法的结果进行对比。设定GA种群初始化规模为20，GA的迭代次数为50次，GA算法的交叉概率为0.8，变异概率为0.2，设定PSO种群初始规模为40，迭代次数为100，ωmax、ωmin分别为0.9、0.4。参数优化如果如下。

① 采用本文改进的GA-PSO算法进行优化时，发现当参数:d=2,σ=0.57,α1=0.92,α2=0.08,C=89时，组合成的组合核函数的分类器具有最优的结果。

② 采用文献[11]方法，即用十重交叉验证与GA算法融合进行对参数的优化的方法，最终的优化参数为：d=2,σ=0.5，α1=0.9,α2=0.1,C=100时，得到了最优的检测效果。

③ 采用传统PSO算法即一次函数方式变化的ω的PSO算法与GA算法进行融合，其具体步骤与本文算法相同，对参数进行优化，得到的优化参数为：d=2,σ=0.47,α1=0.89,α2=0.11,C=33。

④ 采用改进的ω即如式(8)的变化方式的PSO进行参数优化，得到的优化参数为：d=2,σ=0.52,α1=0.89,α2=0.11,C=67。

将不同算法的优化结果的SVM分类器进行训练，对准备好的测试集500张图片分为5组，进行5组试验，得到试验结果如表1所示。

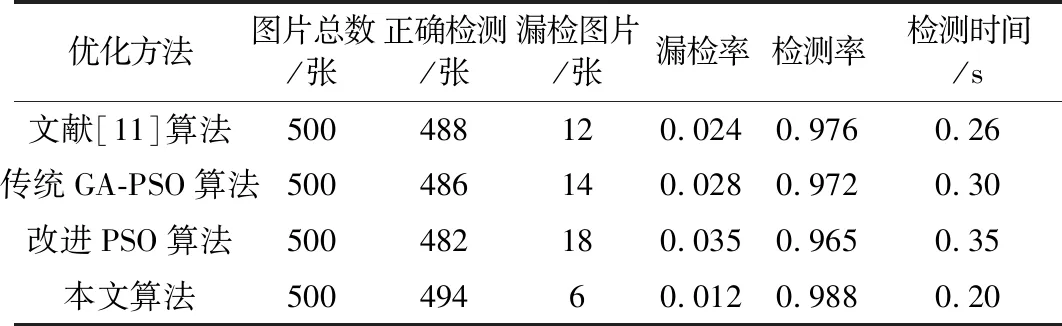
表1 各种方法的最优结果对比

由表1可以发现，与本文结果对比：不同的优化方法得到的优化参数不同，进而得到的效果也不同，用本文的方法优化得到的参数进行行人检测时，检测率最高，并且检测速度相对最快，优化的效果最好，检测效果如图6所示，可以看出，本文算法在不同场景下均有不错的检测效果。

图6 本文算法的行人检测效果图

3 结束语

为了满足当前对识别率以及检测效率的要求，本文对传统算法进行改进。在特征提取方面，本文利用PCA对HOG特征进行降维处理后，大大提高了提取速度；在分类器选择上，将高斯核函数以及多项式核函数按一定比例组合，得到一个组合核函数，同时引进惩罚因子C，并使用改进的GA-PSO对核参数进行优化，经过训练以及测试，数据表明，与传统算法以及比较新的算法在识别率方面都有很大的改进，并且在检测的时间方面，也有很好的结果，满足对检测效率的要求，使行人检测取得满意的效果。