多传感器经纬仪不平行度误差修正方法研究

(中国人民解放军92941部队，辽宁 葫芦岛 125000)

光电经纬仪广泛应用在飞行目标的外弹道测量、测姿、遭遇段脱靶量测量及实况摄录中，目前已成为靶场最重要的测控手段。随着测控任务的拓展，对经纬仪的探测能力、测量精度也提出了更高要求[1]。光电经纬仪机架为三轴(垂直轴、水平轴、照准轴)地平装置，垂直轴铅垂向上，即为测量坐标系的Y轴；水平轴与垂直轴相互垂直；照准轴即为主望远镜中轴线。目前，光电经纬仪逐渐由传统的单一传感器朝多元化方向发展，即在水平轴的轴头或固联在水平轴体上再加装上彩色监视望远镜、红外图像捕获、测量望远镜、大功率激光测距仪、GPS或遥测相位接收天线等多种探测器[2]。但位于水平轴的轴体中央只能放置一个主测量光学成像系统，靶场目前使用的662G光电经纬仪和大口径光电经纬仪等主光轴上放置的都是CCD测量光学系统，而在其下方或上方搭载红外测量系统，如图1所示。虽然经纬仪在出厂前已对两套系统进行标校检测和测角精度校验[3]，尽量使CCD和红外系统两光轴保持平行，并在经纬仪转动时保持同步，但由于实际使用中经纬仪需要经常转场，另受加工工艺和装配技术所限，不可避免地会导致两套测量系统轴系间产生偏差，即产生了不平行度误差。另外，有些靶场为了追求更大的测量视场，专门将多传感器测量系统设计成拼接模式，即使主、辅测量系统光轴保持一定的角度进行摄录，这样在对辅助测量系统测量角度进行计算时，传统的经纬仪跟踪误差修正模型[4]将不再适用，需要建立一套多传感器无照准轴平行约束条件的不平行度误差修正模型。

本文针对这一需求，利用现有脱靶量修正公式与合成原理，提出一种基于坐标转换的不平行度误差修正方法，该方法可以有效地解决多传感器不平行度误差修正问题，具有一定的通用性，能够提高经纬仪非主测量系统的测量精度，满足靶场多感器经纬仪测量数据处理的要求。

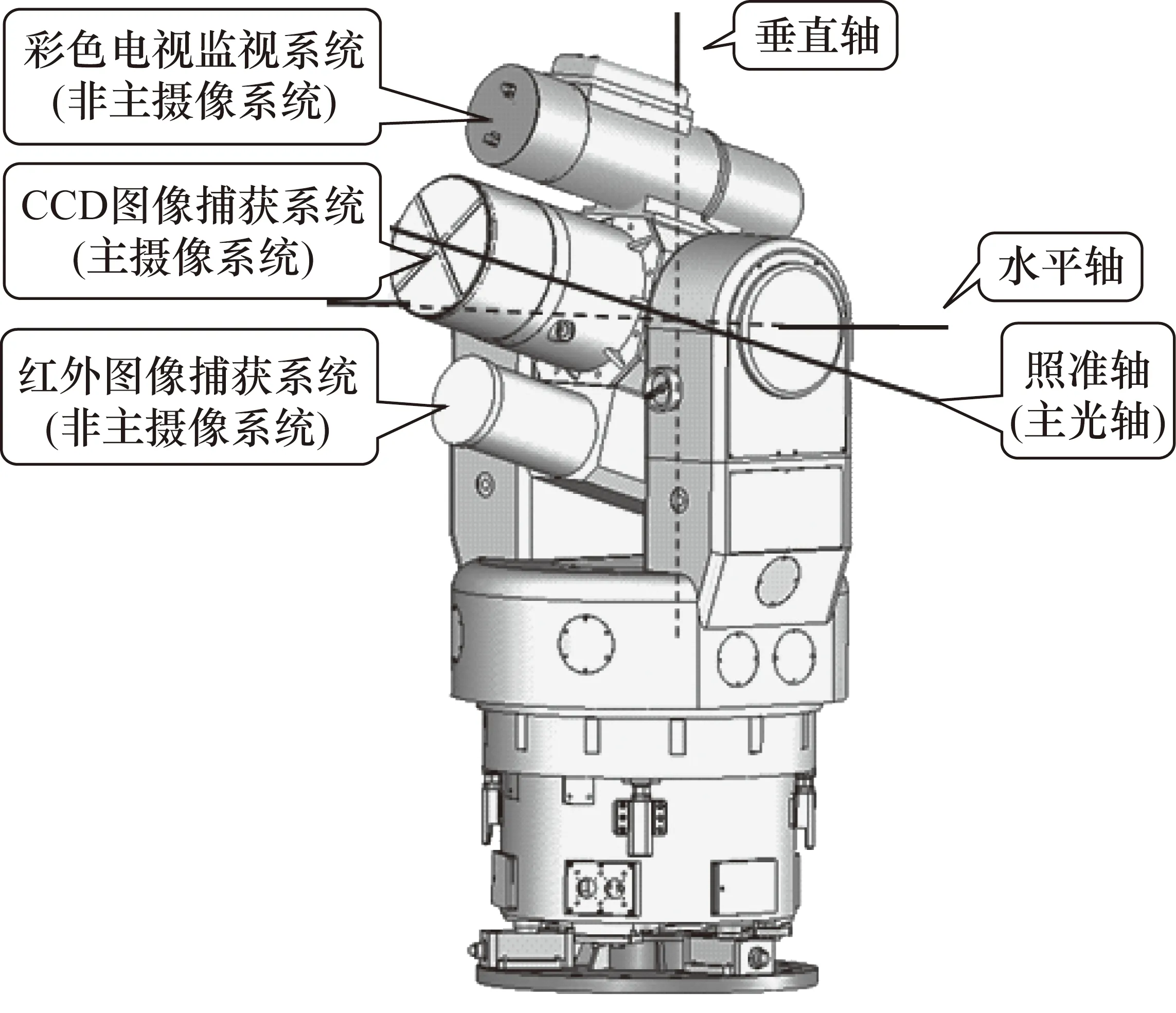
图1 多传感器光电经纬仪示意图

1 脱靶量修正与角度合成

经纬仪通过红外或CCD测量系统捕获目标后，目标在像平面下成像可视为点运动目标。由于经纬仪和操作手响应滞后或跟踪的不稳定性，目标成像位置很难恰好在照准轴中心，因此由刻度盘(或码盘)读出的数据并不是目标真实的方位角和俯仰角，即存在着角度偏差Δα、Δγ，习惯上称为脱靶量[5]。如图2所示，以主镜像平面十字丝中心为原点建立笛卡尔坐标系(下文称像平面坐标系)，通过事后判读可计算出目标像点相对于主光轴中心点的横、纵向偏差，已知光学系统的焦距f，在像平面坐标系下脱靶量计算公式可表示为

(1)

式中，ΔX、ΔY为目标M(判读点位)在像平面坐标系中X、Y方向相对于十字丝中心的距离(像素数×量纲[6])；γ0为该时刻码盘读取的俯仰角值，如图3所示，即主镜光轴(照准轴)OO′与XOZ平面的夹角。这里要说明的是，该脱靶量修正公式是基于光电经纬仪跟踪误差修正模型建立的，必须满足成像系统主光轴与照准轴重合或平行。

接下来，需要把计算出来的脱靶量按绝对时间对经纬仪管控计算机实时采集的方位角α0和高低角γ0信息进行修正，以获得目标M的实际方位角和高低角，这个过程叫作脱靶量合成[7]。经纬仪捕获运动目标在像平面下脱靶量合成角度原理如图3所示，推导过程见文献[8]。

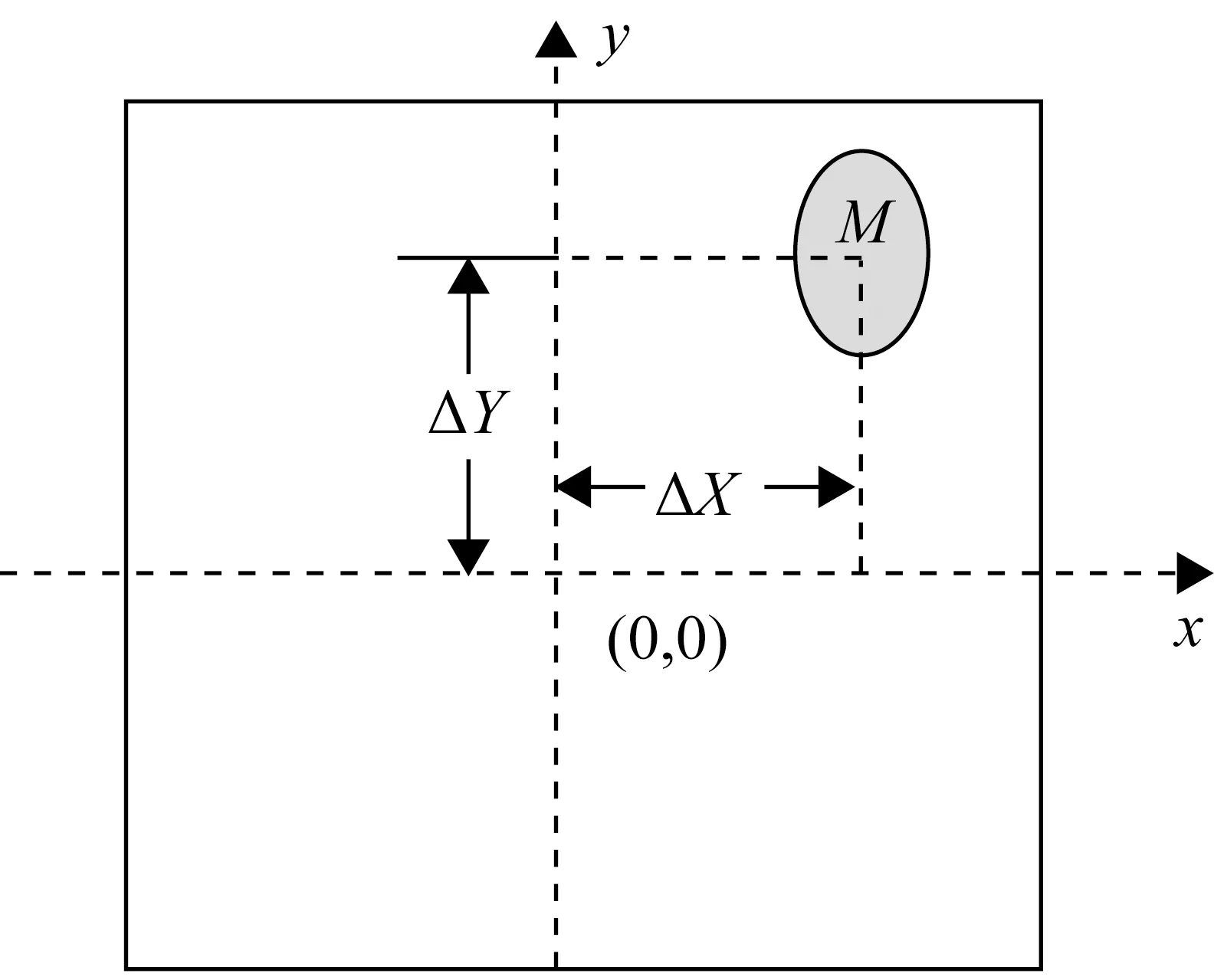
图2 像平面坐标系下脱靶量原理图

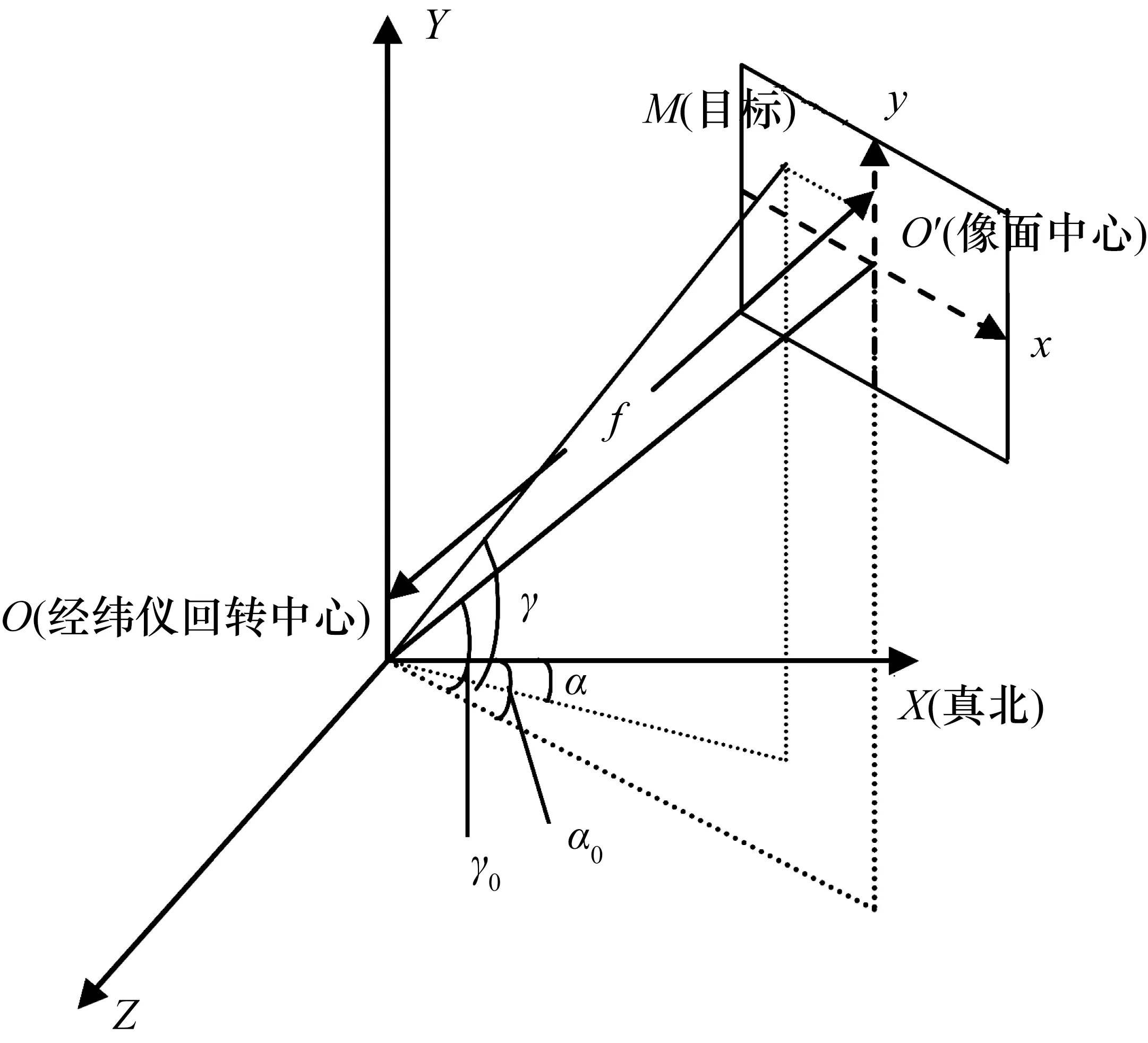
图3 脱靶量合成原理图

当经纬仪挂载了多个传感器，非主测量系统由于不平行差的存在，摄录的目标点在脱靶量合成中包含了不平行度误差，必须予以修正。在经纬仪出厂前，一般要用不平行度检测仪或平行光管进行检测；经纬仪进驻靶场后，一般采用拍远距离方位标或北极星的方式。值得注意的是：不平行度检测时必须拍摄无穷远的目标，否则检测结果中会包含视差的影响[9]。

靶场在检测不平行度时，首先将经纬仪主镜十字丝中心对准无穷远的目标，读取主镜方位角A0和高低角E0的角度综合值，再记录下非主测量系统像面内目标对应角度综合值、方位角A1和高低角E1。两次读数之差即为非主测量系统在方位和高低方向上的视轴不平行度。可用数学表达式表示为

(2)

式中，αd为水平不平行度；γd为垂直不平行度。由于目标很难成像在传感器十字丝中心，所以经纬仪读取的方位和俯仰角度值并不是经纬仪编码器刻度值，而需要进行像平面内脱靶量修正与角度合成。利用脱靶量合成角度公式(式(1))，即得到目标相对该测量系统投影中心的方位角和高低角。

(3)

该修正模型简单，计算方便，但仅适用于经纬仪非主测量系统传感器光轴与主光轴不平行度和视差均较小时使用。当存在较大不平行度误差时，该计算方法不再适用，需引入模型误差。另外，由于受夜间天气能见度的影响，拍星效果有时并不理想，这也在一定程度上影响了靶场计算不平行度的精度。本文将力求建立通用不平行度误差修正模型，同时详述非主测量系统目标脱靶量合成角度过程。

2 非主测量系统不平行度误差修正

当非主测量系统光轴与经纬仪照准轴存在较大不平行度时，采用坐标变换的方法将目标在非主测量系统像平面下的投影点转换成经纬仪测量坐标系下的角度值，即修正了光轴与照准轴间不平行的脱靶量误差。这里，以经纬仪多个传感器测量系统建立3个坐标系，坐标系关系如图4所示，下面给出具体定义。

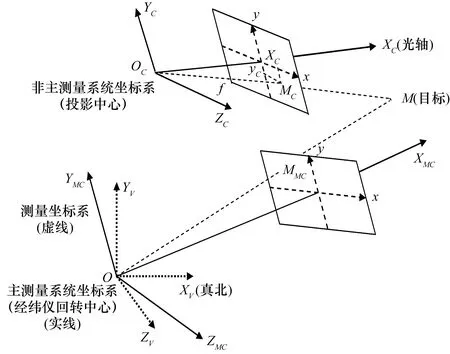
图4 多传感器经纬仪坐标系关系图

① 主测量系统坐标系(OXMCYMCZMC)：原点O是经纬仪的回转中心；X轴与照准轴重合，指向目标；Y轴与垂直轴重合；Z轴与水平轴重合。

② 测量坐标系(OXVYVZV)：原点O是经纬仪的回转中心；X轴过原点，指向大地北；Y轴过原点，铅垂向上；Z轴过原点，与X、Y轴构成右手直角坐标系。

③ 非主测量系统坐标系(OCXCYCZC)：原点OC为非主测量系统的投影中心，位于光轴上；X轴与非主测量系统光轴重合，指向测量方向；Y轴过原点，平行于像平面坐标系y轴；Z轴过原点，平行于像平面坐标系x轴。

需要说明的是：为直观起见，使目标成正像，将像平面移到了投影中心的前方；在非主测量系统坐标系中，上文提到的像平面坐标系即指在该测量系统像平面与光轴交点为原点建立的笛卡尔坐标系。

设经纬仪搭载的非主测量系统光轴水平不平行度为αd，垂直不平行度为γd。当主测量系统跟踪动目标以经纬仪轴系做旋转时，目标在其像平面的投影坐标与目标在非主测量系统坐标系下像平面的投影可理解为坐标平移的关系，即投影点绕Y轴顺时针旋转αd角度，绕Z轴顺时针旋转γd角度，再将主测量系统坐标系原点平移到非主测量系统坐标系原点，此时两个投影点重合。那么，非主测量系统坐标系到主测量系统坐标系的转换关系[10]可表示为

(4)

其中，

式中，(xmc,ymc,zmc)为目标M在主测量系统坐标系下的坐标，其坐标值可通过判读目标点在CCD像面上的位置得到；(xco,yco,zco)为非主测量系统坐标系原点在主测量系统坐标系下的坐标，其坐标值可通过实际测量或计算经纬仪系统参数得到；(xc,yc,zc)为目标在非主测量系统坐标系下的坐标，由三角形几何关系可得：

(5)

根据脱靶量合成角度公式(式(3))得目标M在非主测量系统坐标系下的方位角αc和高低角γc为

(6)

(7)

将上述参数代入关系式(4)即可求得目标在主测量系统坐标系下的坐标。同理，主测量系统坐标系到测量坐标系的转换关系可表示为

(8)

其中,

那么，目标M在测量坐标系下的方位角α和高低角γ可表示为

(9)

(10)

上述表达式即为非主测量系统脱靶量合成角度公式，由于是建立在坐标系转换关系上，故该不平行度误差修正方法不受测量系统平行度约束条件限制，具有一定通用性。

3 试验验证

下面以靶场某次导弹飞行试验任务为例来验证本文方法的修正效果。测控装备采用某固定站点光电经纬仪，安装有CCD和红外两个测量分系统。红外测量系统搭载于主CCD摄录系统下方并刚性连接，跟踪目标时随主测量系统绕经纬仪轴系一起转动。试验任务中，红外和CCD测量系统实时无压缩记录和存储目标图像和位置信息。导弹尾部安装有靶场GPS-1测量系统[11]，采用WGS-84坐标系定位，用球坐标转换的方法将目标GPS定位信息转换到红外测量系统投影中心OC(如图4所示)，转换后测角精度为0.01×10-3rad,转换后的方位、俯仰角度作为真值，记为α真、β真；目标在经纬仪CCD和红外传感器上成像后判读位置均为导弹尾部曳光管火焰中心，红外测量系统实际测量的合成角度值，记为α测、β测；用本文方法修正红外测量系统的不平行度误差，计算出修正后合成角度值，记为α修、β修；靶场现用方法修正后合成角度值，记为α现、β现。那么，未经修正实测红外传感器角度误差可表示为：Δα=α测-α真，Δβ=β测-β真，如图5、图6中蓝色线；经本文方法修正后的角度误差可表示为：Δα′=α修-α真，Δβ′=β修-β真，如图5、图6黑色实线；靶场现用方法修正后的角度误差可表示为：Δα″=α现-α真，Δβ″=β现-β真，与本文修正方法修正后的角度误差比对结果如图7、图8所示，其中靶场现用方法用蓝色虚线表示，本文修正方法用黑色实线表示。

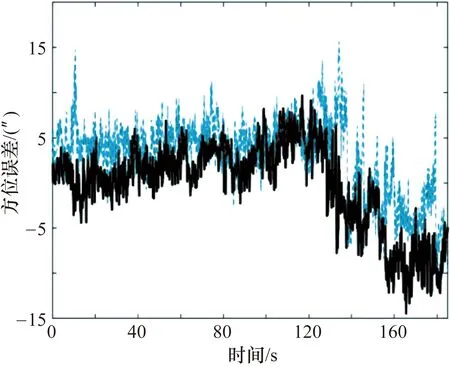
图5 本文方法与未修正方位误差比对图

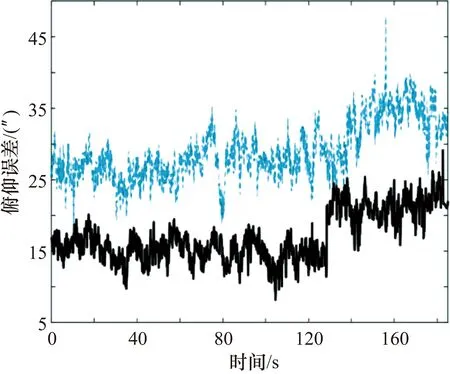
图6 本文方法与未修正俯仰误差比对图

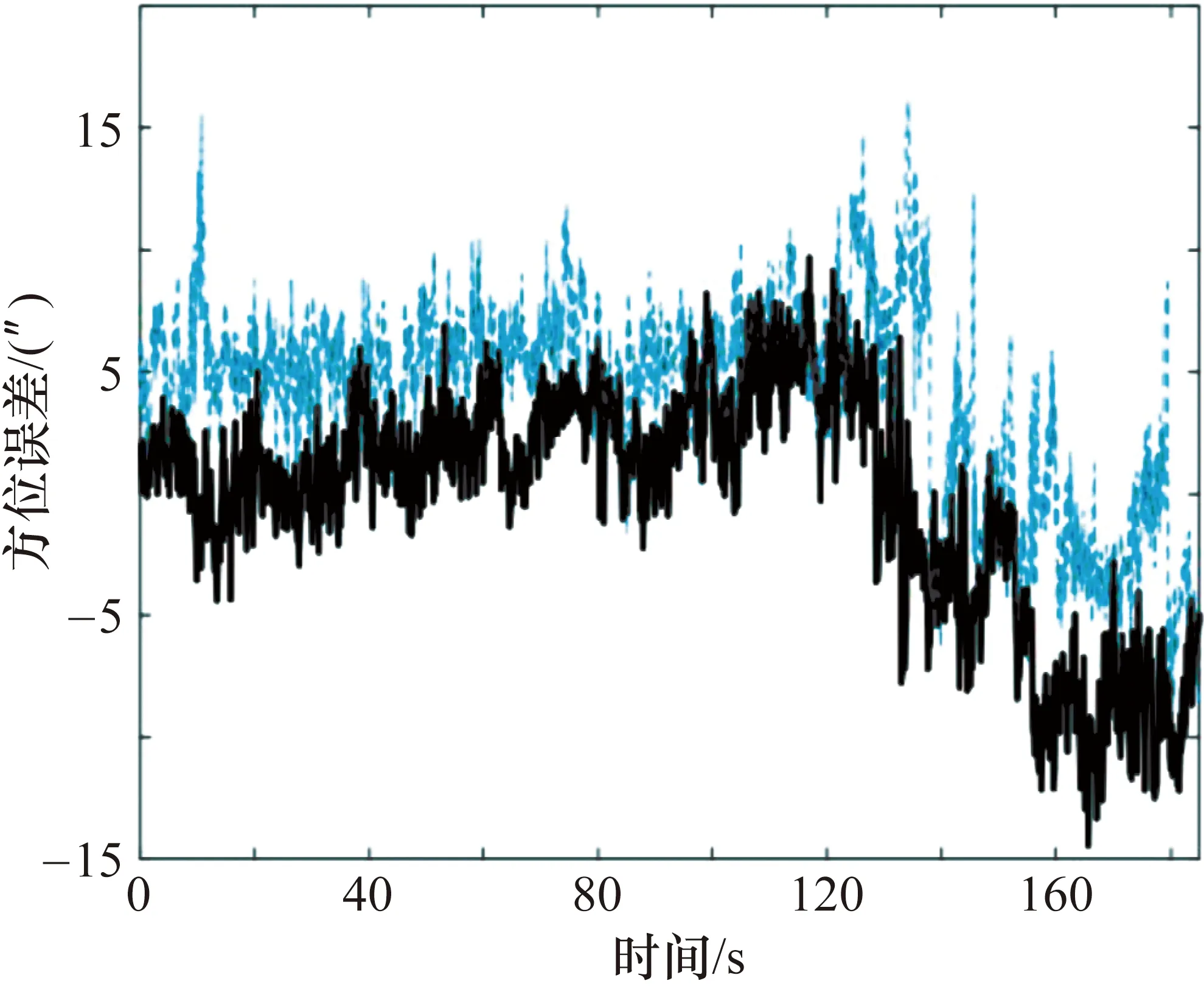
图7 本文方法与现用方法方位修正误差比对图

图8 本文方法与现用方法俯仰修正误差比对图

修正误差比较方位角均值方位角均方差俯仰角均值俯仰角均方差未修正角度误差6.183.9828.984.00现用修正方法4.183.0119.565.06本文修正方法3.722.5617.003.45

通过对非主测量系统不平行度误差的修正，由图5～图8可知，经本文方法修正后红外传感器测角数据更加接近真值，由于本文修正后角度数据是通过坐标转换方法获得的，从而避免了目前靶场在拍星计算不平行度时所带入的各类系统误差，也减少了人力投入和误差源对修正结果的干扰。由于靶场目前使用的经纬仪红外传感器在CCD传感器正下方(如图1所示)，因此不平行度误差对方位角影响相对要小，对俯仰方向影响会比较大。由于俯仰方向含有大气折射误差，所以与GPS真值做差后残差略偏大[12-13]属正常。表1统计结果表明，本文方法能够很好地解决不平行度问题，并有效地提高了非主测量系统的测角精度，修正后误差明显小于靶场现用方法。修正前后均方差属于一个量级，说明不平行度误差主要是由多传感器轴系误差引起的测角偏差，在经纬仪跟踪目标转动时，不平行度对随机误差的影响并不大[14]。通过与转换后GPS角度真值比对做误差分析，证明本文方法可将光电经纬仪非主测量系统的测角精度控制在5″之内，大幅提高了靶场测控装备的测量精度。

4 结束语

本文分析了多传感器经纬仪跟踪测量原理，利用多传感器坐标系间转换关系及脱靶量合成角度原理建立不平行度误差修正模型。目前多传感器经纬仪在靶场使用日益广泛，出厂前一般都进行了不平行度静态精度检测，水平和垂直误差已控制在了一定范围之内，用靶场现有方法也可以快速消除一部分不平行度误差，文中给出了具体误差修正和角度合成方法。针对存在较大不平行度的修正，建立了通用模型，对非主测量系统安装位置不再受限制，且修正精度更高，具有一定推广价值。