孤子内波环境下三维声传播建模*

张泽众 骆文于† 庞哲 周益清

1) (中国科学院声学研究所,声场声信息国家重点实验室,北京 100190)

2) (中国科学院大学,北京 100049)

提出了一种适用于存在孤子内波水平变化波导的高效三维水下声场计算模型.该模型忽略反向散射,一般情况下由于孤子内波的反向散射非常弱,所以该模型能够提供精确的三维声场结果.同时,相对于双向三维耦合简正波模型,该模型在计算效率上能够至少提高一个数量级.除了孤子内波环境之外,本模型还适用于存在小尺度海脊等反向散射比较弱的一般水平变化波导环境.本文用该模型计算由KdV方程得到的孤子内波问题,并用双向三维耦合简正波模型作为标准模型来验证本模型的计算精度.计算结果表明本模型在反向散射比较弱的波导环境中具有非常高的计算精度.

1 引 言

作为一种中尺度海洋现象,内波对水下声传播具有显著影响.因此,在过去的几十年中人们对内波问题做了大量研究[1-15].

王宁等[1]通过分析2005年黄海实验结果,研究了内波和潮汐引起的宽带正常模态振幅波动和深度的相关性.马树青等[2]研究了浅海孤子内波对水下声传播和声源定位的影响,并且发现当孤子内波通过接收阵列时传播损失会产生5 dB左右的波动.1995年浅海随机介质实验(SWARM)通过研究孤子内波存在时声信号的变化对浅海宽带声信号进行了分析,发现其时间波动在深度上是同步的,并依赖于水体的变化,且利用水平折射对该现象进行了解释[3].2006年浅海实验(SWARM'06)对孤子内波存在下低频声场的波动进行了研究,发现在孤子内波通过期间,水平折射效应对声场造成了很大的影响[4].Lin等[5]研究了截断内波导管末端的声辐射效应.Colosi[6]使用耦合简正波方程模拟了孤子内波存在时接收器位置的声波强度,Yang[7]利用该方程建立了模式耦合矩阵.

人们对孤子内波环境下三维声传播建模也进行了大量研究,针对孤子内波环境开发出了很多声传播模型.考虑到计算效率,大多数模型基于抛物方程理论[8-10].针对孤子内波问题,本文提出一种基于耦合简正波理论的高效三维耦合简正波模型.

Ferla等[11]开发的C-SNAP模型是计算水平变化环境中声场的二维耦合简正波模型.因为它基于步进式算法,所以在计算效率方面该模型并不逊于现有的抛物方程模型.C-SNAP模型使用阻抗匹配边界条件以保持比较高的精度.本文提出的三维模型利用C-SNAP计算相应的二维线源解,然后利用傅里叶变换技术得到三维声场解.我们利用骆文于等[12,13]开发的双向耦合简正波二维模型DGMCM2D以及三维模型DGMCM3D[14]作为标准模型来验证本模型的计算精度并比较计算效率.

本文结构如下：第2节介绍三维单向耦合简正波模型的理论基础.第3节首先利用本模型计算孤子内波环境下的声场数值解,并与双向耦合简正波模型DGMCM3D得到的结果进行对比; 其次数值仿真同时存在孤子内波和海脊时的声场,以表明本模型具有处理一般弱反向散射特征水平变化波导问题的能力.第4节给出总结和结论.

2 理 论

下面首先简要回顾二维单向耦合简正波模型C-SNAP,并分别给出二维点源问题和线源问题的解; 然后介绍如何利用傅里叶变换方法将该二维模型扩展为三维模型; 最后简单介绍本文采用的孤子内波模型.

2.1 C-SNAP模型

C-SNAP模型是由Ferla等[15]提出的,它是一个二维单向传播耦合简正波模型.如图1所示,对于水平变化波导问题,我们将波导中水平变化区域在距离上分为若干段,每一段均视为水平不变的波导环境.

图1 水平变化波导(红色虚线)的阶梯近似Fig.1.Stair step approximation of a sloping bottom (red dashed line).

首先考虑柱坐标系下的二维点源问题.取时间因子 exp(iωt) ,第j段(Sj)内的声场可以表示为：

其中 Mj为第j段简正波号数,rj-1和 rj分别为第j段的左边界和右边界是0阶第二类Hankel函数分别是第j段中第m号简正波的水平波数和本征函数.在第一段(S1)中,设定 rj-1=r1,则第一段的模式系数为

其中 zs表示声源深度.

C-SNAP模型利用Collins和Westwood[16]提出的阻抗匹配边界条件以取得更高的精度.考虑第j个竖直边界(Sj和 Sj+1之间的边界),注意到在 Sj+1段的左边界上约化Hankel函数的值为1,因此在边界 r=rj上有如下边界条件：

对(3)式两侧均施加如下运算：

并利用简正波本征函数的正交归一性质,可以得到Sj+1中模式系数的表达式：

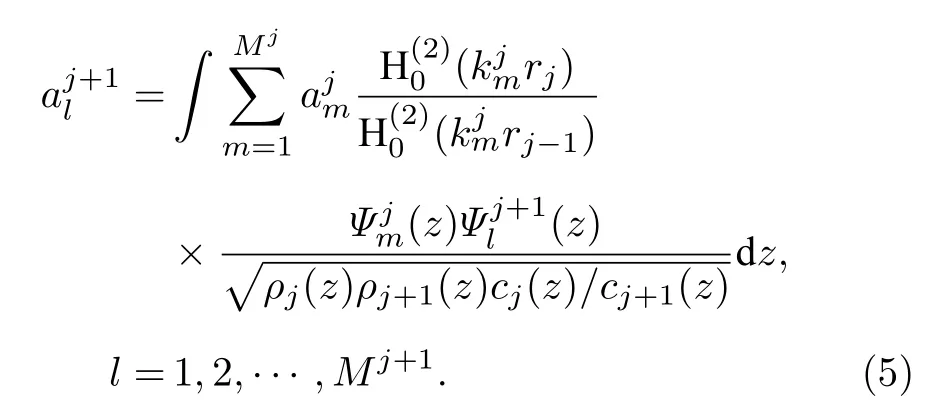
将(1)式代入(5)式可得

由(6)式可知,只需要前一段随深度变化的声压和本段的本征函数就可以得到本段的模式系数.

下面考虑直角坐标系中的二维线源问题.将第j段(Sj)中的声场表示为

第一段中的模式系数为

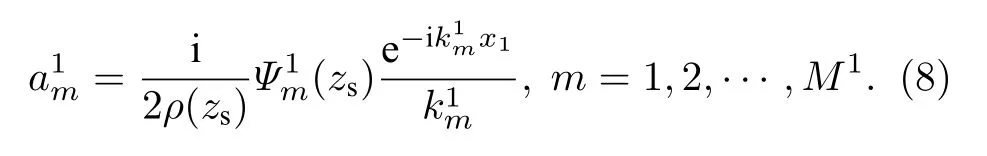
类似于点源问题,可以得到如下所示的第j个竖直边界上的阻抗匹配边界条件：

对（9）式两侧均施加(4)式中的运算,并利用简正波本征函数的正交归一性质,可以得到 Sj+1段的模式系数：

以上即为C-SNAP模型的理论基础,由此可以看出,C-SANP是一个利用阻抗匹配边界条件的二维单向传播耦合简正波模型.当反向散射可以忽略时,C-SNAP模型可以快速得到比较精确的声场近似解.

2.2 三维单向耦合简正波模型

笛卡尔坐标系下三维亥姆霍兹方程为[17]：

点源坐标为 (xs,0,zs).本文使用如下傅里叶变换对

对(11)式两侧同时施加运算

可得

二维线源的亥姆霍兹方程为[17,14]

通过比较(15)式和(16)式,发现这两个方程形式相同,只不过(15)式中左侧第三项的因子为因而(16)式中对应的因子为 k2.对于不同的 ky值,可以用二维模型得到对应的二维线源解这样,可以先计算一系列然后经过反傅里叶变换就可以得到三维声场解p(x,y,z).

由上可知,为了得到三维声压 p(x,y,z) ,需要对 ky进行积分.为了避免数值溢出问题,我们利用围线积分来代替实轴上的积分[18,19]，积分路径如下所示(参见图2)：

在该积分路径上,(13)式变为

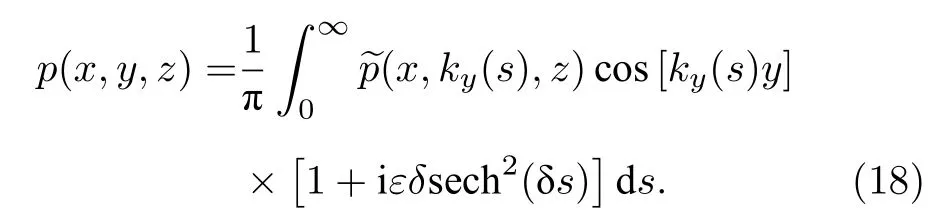
其中 δ=1/(6Δs) ,Δs=(kmax-kmin)/(Ns-1),ε=3Δs/(2πloge),Ns表示总积分采样点数.

图2 反傅里叶变换的积分围线(圆圈代表简正波的本征值,即水平波数)Fig.2.Complex integration contour for evaluation of the wavenumber integral.The dots indicate horizontal wavenumbers of the normal modes.

由于本文提出的三维模型是对二维模型利用傅里叶变换技术扩展得到的,因此该三维模型的精度和计算效率是由二维模型决定的.由后面给出的数值算例结果可以看出,对于孤子内波问题,相对于DGMCM2D模型,C-SNAP模型能够提供比较精确的数值解,然而在计算效率上C-SNAP则至少提高了一个数量级.一般情况下由于孤子内波的反向散射可以忽略不计,本文提出的三维模型能够快速提供比较精确的孤子内波问题的三维声场结果.

2.3 孤子内波模型

假设孤子内波的波阵面为平面,海面为理想边界条件,海底为半液态介质,如果满足浅海条件,则单个孤子内波KdV方程的双曲正割剖面解为[2]

其中 Δ 代表波包宽度,A0为孤子内波的幅度,x0=vt为孤子内波波包的位置,v是孤子内波的传播速度.

3 数值模拟

下面首先考虑平海底条件下存在孤子内波的情况,以验证本文提出的三维模型的计算精度与效率; 然后考虑同时存在内波和海脊,且海脊高度相对较小的情况.在下面的数值计算中,利用双向耦合简正波模型DGMCM2D和DGMCM3D提供二维和三维声场的标准解.

3.1 声速剖面

考虑浅海负温跃层的波导环境,声速剖面表达式为

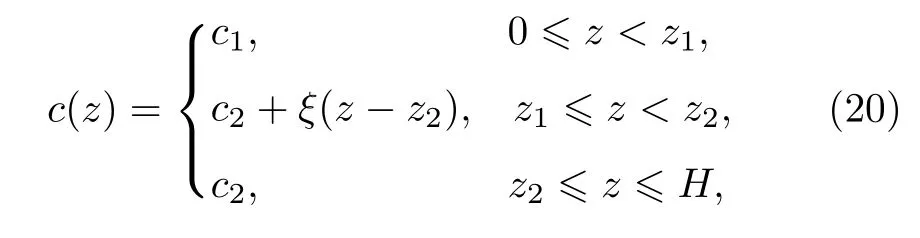
其中 ξ=-5(m/s)/m 为温跃层的声速梯度,c1=1500 m/s,c2=1400 m/s,z1=20m ,z2=40m ,H=100m.海底声速,密度和吸收系数分别为2000 m/s,2.0 g/cm3和0.1 dB/λ.

图3给出了用于数值模拟的波导环境.图3(a)为无孤子内波时的浅海负温跃层的声速剖面; 图3(b)给出了存在孤子内波时的声速剖面,孤子内波波包在距声源4 km处,其中 A0=20m ,Δ=100m ,x0=4km; 图3(c)为同时存在孤子内波和海脊时的波导环境,海脊在距声源6 km处.声源和接收器的深度分别为10 m和70 m,声源频率为25 Hz.

3.2 孤子内波问题的二维声场结果

图4给出在无孤子内波和存在孤子内波时DGMCM2D和C-SANP得到的两组二维声场计算结果,其中双向耦合简正波模型DGMCM2D被用作标准模型.从该图可以看出：

1)两组结果存在较大差异,表明孤子内波的存在对声传播有显著影响;

图3 二维声速剖面示意图 (a)无孤子内波的声速剖面;(b)孤子内波位于4 km处的声速剖面; (c)孤子内波位于4 km处,海脊位于6 km处的声速剖面Fig.3.Sound speed fields considered in this paper：(a) The background sound speed field; (b) in the presence of an internal wave soliton,centered at range 4 km from the source;(c) in the presence of both an internal wave soliton centered at 4 km and a cosine-bell shaped bottom ridge centered at 6 km from the source.

2)两组结果在4 km (孤子内波位置)之前基本重合,表明孤子内波产生的反向散射可以忽略不计;

3)在每组结果中,C-SNAP与DGMCM2D的结果基本一致,表明对于该问题,C-SNAP的结果具有非常高的计算精度.

此外,对于该问题,DGMCM2D和C-SNAP的运行时间分别为94.7 s和5.3 s,可见C-SNAP在计算效率上比DGMCM2D至少提高了一个数量级.因此,本文提出的三维模型更适于计算内波问题的三维声场.

图4 孤子内波环境下DGMCM2D和C-SNAP在70 m深度传播损失曲线 蓝色实线和红色虚线分别表示无孤子内波时DGMCM2D和C-SNAP的计算结果,绿色和枚红色虚线分别表示孤子内波波包在4 km时DGMCM2D和CSNAP的计算结果,黑色虚线表示孤子内波波包位置Fig.4.Transmission loss results for the internal solitary wave problem computed by DGMCM2D and C-SNAP.The blue solid line and red dashed line are the results by DGMCM2D and C-SNAP for the case without internal waves,respectively,and the green and magenta dashed lines are the results by DGMCM2D and C-SNAP for the case with a soliton located at range 4 km,respectively.The black dashed line indicates the center of the soliton.

3.3 孤子内波问题的三维声场结果

此处三维双向耦合简正波模型DGMCM3D被用作标准模型.图5分别给出DGMCM3D和本文提出的三维模型在70 m深度水平面上的三维声场计算结果.图6给出纵向距离 y=0km ,深度z=70m的随距离x的传播损失曲线.从图5和图6可以看出本文提出的三维模型的结果与DGMCM3D的结果非常一致,表明本文提出的三维模型对内波问题具有非常高的计算精度.此外,DGMCM3D和C-SNAP3D的计算时间分别为1616.2 min和94.45 min.此外,图5中在内波以远的区域发现除了与距离有关的干涉现象,还存在明显的与角度有关的干涉现象.

3.4 同时存在孤子内波和海脊时的三维声场结果

为了验证本模型适用于反向散射很弱的一般水平变化波导问题,考虑孤子内波和海脊同时存在的情况.图7是三维海底地形图,海脊在距声源处,截面形状为宽度100 m,高度10 m的余弦函数,海底深度可以表示为：

选择高度较小的海脊来保证反向散射可以忽略.图8给出DGMCM2D模型和C-SNAP模型在70 m深度的随距离变化传播损失曲线,可以看出两组计算结果基本一致,表明海脊高度为10 m时反向散射可以忽略不计.对于存在海底起伏的情况,如下因素会综合影响反向散射强度：斜坡角度、斜坡高度、斜坡海底声阻抗与海水声阻抗的比值等.文献[20]对这个问题进行了比较详尽的讨论.

图9分别给出DGMCM3D模型和本文提出的三维模型得到的三维声场计算结果,可以看出两者非常一致,表明本文提出的三维模型也适用于反向散射可以忽略的一般水平变化波导问题.此外,DGMCM3D和C-SNAP3D的计算时间分别为4778.8 min和324.3 min.

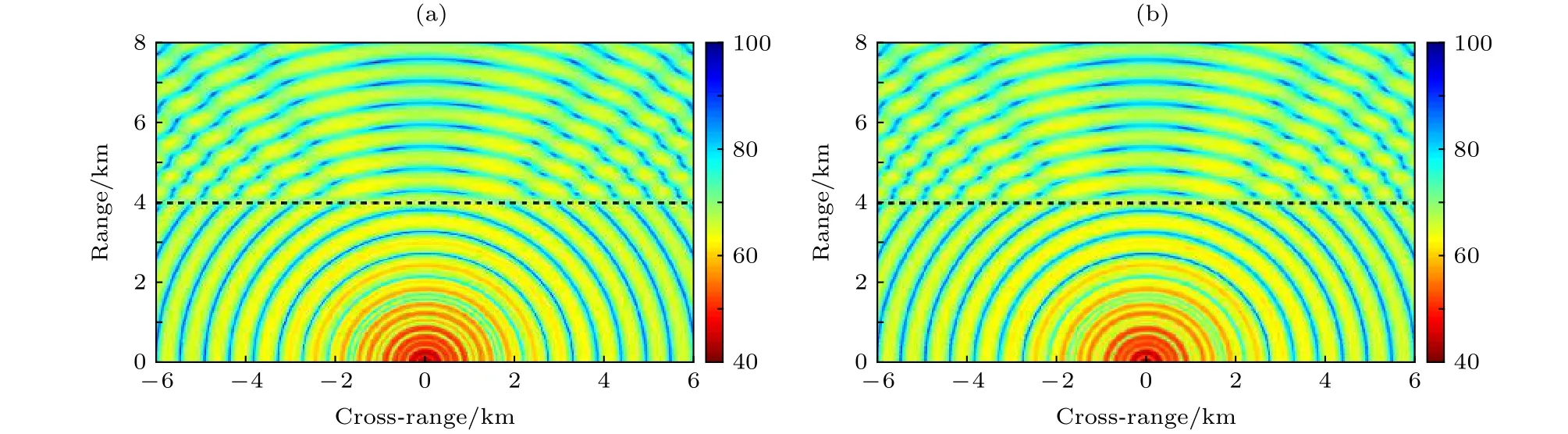
图5 70 m深度水平面上的三维传播损失结果 (a) DGMCM3D的结果; (b)本文提出的三维模型的结果,黑色虚线代表孤子内波波包的位置Fig.5.Three-dimensional transmission loss results in the horizontal plane at depth 70 m computed by (a) DGMCM3D and (b) the present 3D model.The center location of the internal wave is indicated by dashed black lines.

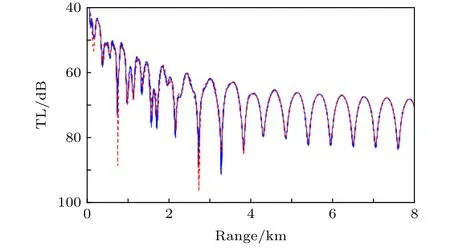
图6 纵向距离 y=0km ,深度z=70 m,随距离传播的损失曲线,蓝色实线和红色虚线分别为DGMCM3D和本文提出的三维模型的结果Fig.6.Transmission loss lines versus range along the crossrange y=0km at depth z=70 m computed by DGMCM3D (the blue,solid curve) and the present 3D model(the red,dashed curve).

图7 海底存在海脊的水平变化波导示意图Fig.7.Geometry of a range-dependent waveguide with a bottom ridge.

图8 孤子内波和海脊同时存在时深度70 m处的二维传播损失结果,其中蓝色实线为DGMCM2D结果,红色虚线为C-SNAP结果Fig.8.Two-dimensional transmission loss results at a depth of 70 m for the problem involving a solitary internal wave as well as a bottom ridge by DGMCM2D (the blue,solid curve) and C-SNAP (the red,dashed curve).

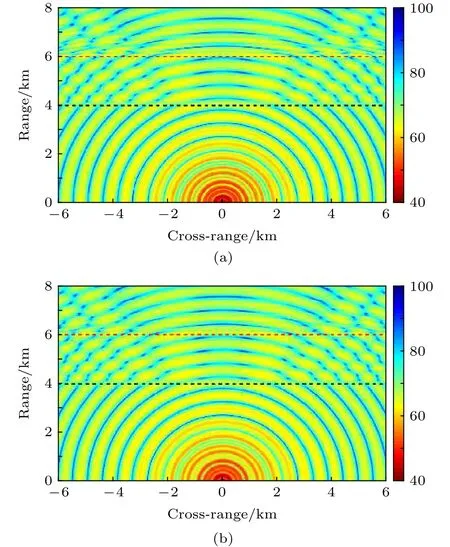
图9 同时存在孤子内波和海脊时深度70 m水平平面上的三维传播损失 (a) DGMCM3D结果; (b)本文提出的三维模型的结果.黑色和红色虚线分别表示孤子内波波包和海脊中心的位置Fig.9.Three-dimensional transmission loss results in the horizontal plane at depth of 70 m in the presence of a solitary internal wave as well as a bottom ridge computed by(a) DGMCM3D and (b) the present 3D model.The center locations of the internal wave and the ridge are indicated by dashed black and red lines,respectively.

4 结 论

作为一种二维单向耦合简正波模型,C-SNAP在处理二维水平变化波导问题时具有非常高的计算效率.本文将其扩展为一个高效的三维耦合简正波模型,对孤子内波等反向散射非常弱的问题,该模型能够提供高效精确的三维声场结果.

本文数值模拟了存在孤子内波时的三维声场.由于一般情况下孤子内波产生的反向散射可以忽略不计,本模型三维结果与DGMCM3D的结果非常一致,然而本三维模型在计算效率上比DGMCM3D至少提高了一个数量级.此外,从本文考虑的数值算例结果我们发现由于孤子内波的影响,在孤子内波后方区域可能会出现依赖于角度的相干干涉.最后,在孤子内波和海脊同时存在的条件下验证了当反向散射可以忽略时,本文提出的三维模型也适用于一般的水平变化波导问题.