高职院校高等数学中换元积分法的教学研究

吴丽娇 福建船政交通职业学院 福建福州 350000

高等数学作为一门重要的基础课程,可以有效训练学生的抽象思维与逻辑思维能力,但由于高职院校学生的数学基础比较薄弱,学习不定积分时特别困难.凑微分法即第一换元积分法是解决不定积分的重要方法,是学习微分方程,多元函数重积分的基础.因此,针对这种情形,本文结合实际的教学经验,对凑微分法进行探讨研究以解决学生学习凑微分法困难的矛盾.

1.换元积分法中的凑微分法

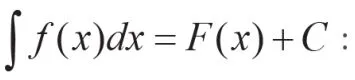
1)当被积函数是单独的复合函数时:

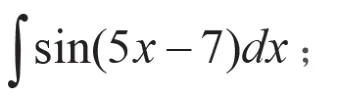
2)当被积函数在基本公式中没有,但形式上接近时,可以此公式为目标公式靠近从而求解:

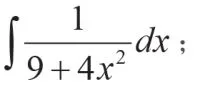
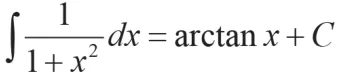
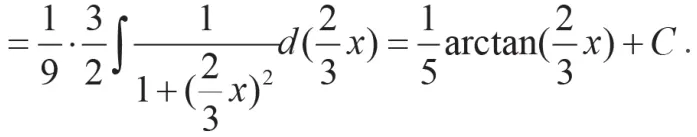
2.分部积分法中的凑微分法

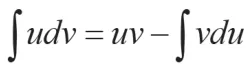
解析:无论留下哪个函数作为被积函数都不能满足凑微分法的条件,此时尝试分部积分.

解

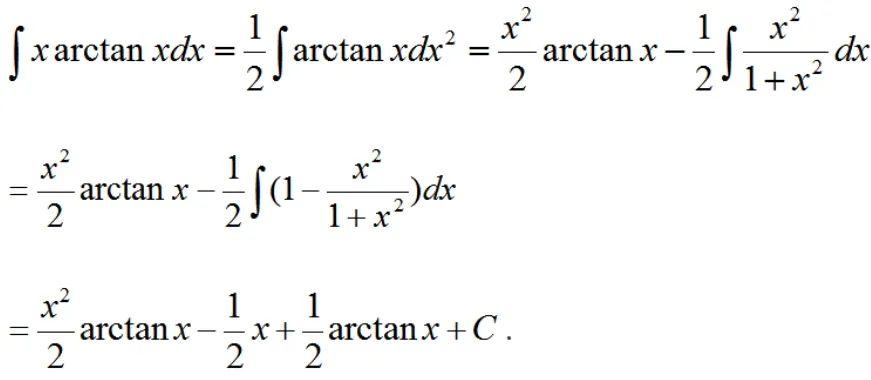
这些例子仅仅是最常见的凑微分的基本类型,并且是一次凑微分即可求解.它是最基本的凑微分类型.我们应先熟悉这些基本类型,学会融会贯通才能进一步学习诸如多次凑微分,第二换元积分法等复杂的方法.在教学过程中实施上述基本类型的讲练结合法,学生能够快速、有效地掌握不定积分的凑微分,并且效率与成功率也有所提升.当然,学习不定积分的凑微分法并非仅仅是教会学生解题,更重要的是引导学生掌握方法的基础上对其体现的数学思想进行挖掘,探寻其背后的本质,使学生真正领会到学习高等数学微积分的魅力!