智能物流最短配送路径选取优化模型分析

贺 琳

(阜阳师范学院，安徽 阜阳 236037)

随着物流产业的发展，对物流的配送路径优化研究受到人们的极大重视。通过对物流配送路径的智能选取，能够降低物流配送中的经济开销，促进物流经济发展。采用大数据信息处理技术进行物流配送路径优化，结合智能物流调度技术，分析物流配送路径优化对物流经济发展的关系模型，分析智能配送路径选取对物流经济发展的影响，挖掘智能配送路径选取对物流经济发展的影响大数据量化特征，结合特征提取和信息融合的方法，可以提高物流经济的发展水平[1]。对此提出一种基于最短路径规划和面板数据检验的智能配送路径选取对物流经济发展影响的建模方法，构建智能配送路径选取对物流经济发展的统计特征分析对象模型，结合多元线性融合方法进行智能配送路径选取，对物流经济发展因子进行分析。结合模糊约束控制方法，实现物流智能配送路径优化，并实现智能配送路径选取技术对物流经济发展影响的建模，最后进行实证分析，得出有效性结论。

1 物流配送路径选取优化模型

1.1 智能物流配送路径的组网设计

为了实现对智能配送路径选取对物流经济发展准确评估，采用最短路径规划和统计特征量化评估方法进行智能配送路径选取[2]，结合物流交通路网组网结构模型进行最短路径规划，用路段和交叉口组成的网络分析物流路径，物流路径规划的网络组网结构模型为：

(1)

其中，i(t)和s(t)分别标记物流配送路径的节点位置和路径规划长度，当t>δ时，采用Small World网络模型构建物流配送的SIRS模型[3]，智能配送路径选取的动力学模型可以描述为：

(2)

计算物流配送路径的路段阻抗，进行配送路径的动态选址网络规划设计，当路段的流量为0时，物流配送路径的选取问题为一个线性规划问题[4]，设Power-Law结构中有m个物流配送Sink节点，表示为A1,A2,…,An，每个节点进行物流配送的负载量为a1,a2,…,an，采用最短路径搜索进行物流配送路径的线性规划设计，得到物流配送调度运输问题数学表达：

(3)

(4)

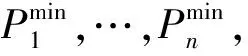
N=Nt+1,Nt≥0

(5)

C表示节点i的最大传输概率密度函数，在线性规划条件下，得到物流配送的路网拓扑结构描述为：

(6)

建立一种基于粗糙集理论下的物流配送路径动态搜索模型，结合自适应路径规划和寻优控制，提高路径规划能力[6]。

1.2 物流配送路径优化规划

采用最短路径寻优方法进行智能配送路径选择，采用量化回归分析方法构建智能配送路径选取与物流经济发展的大数据统计分析模型[7]，得到物流配送路径的线性规划数据集为n，物流路径选取对物流经济发展的促进性特征分布矩阵为一个n×n的矩阵：

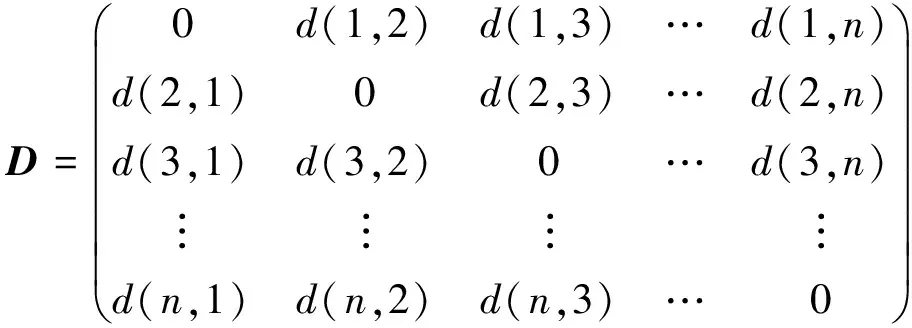
(7)

(8)

将任意的物流配送中心数据点xi和xj之间的最大相似度特征量，描述为s(i,j)，其值越小，表示物流路径规划的动态性越好，则相似度越小，表示物流路径规划的适应度越差。根据上述算法设计，进行物流路径空间规划设计，得到物流配送路径选择的路径规划样本集X={x1,x2,…,xn}，找到k个聚类中心{a1,a2,…,ak}，对采用模糊均值聚类方法进行物流经济发展的统计学建模，得到物流配送路径规划对物流经济发展影响的统计量为：

flg-M(z)=flg(z)+hxflg(z)+hyflg(z)

(9)

其中，flg(z)为配送路径聚类统计量，hx为配送路径相似度，hy为配送路径的适应度。遍历整个物流配送路径规划的网络模型，计算物流配送区域U内的任意一个物流配送节点的负载量，得到物流配送路径对物流经济发展的整体适应度模型描述为：

(10)

其中，n为电子商务环境下物流配送中心分布粒子的个数。设定m0个结点通过2×(m0-1)条向量节点进行路径规划设计，以概率1-p生成一个结点模型，得到平均适应度，结合平均适应度水平进行量化回归分析。

2 物流配送路径对物流经济发展的影响建模

2.1 描述性统计分析和物流经济发展影响变量模型

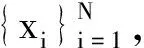
E′c=E′TX+E′RX

(11)

E′c=Nk1LDA+Nk2+Ec=(N+1)k1LDA+k1LA+(N+2)k2

(12)

(13)

其中，N为统计特征量。考虑智能配送路径选取对物流经济发展的统计特征预测值，采用均衡调度方法进行大数据采样，结合最佳配送路线进行面板数据分析。

(14)

用量化回归分析方法构建智能配送路径选取与物流经济发展的描述性统计分析模型，得到描述性统计特征量为：

(15)

当R2TR2={Xd+1,Xd+2,…Xd+m}{Xd+1,Xd+2,…Xd+m}T时，智能配送路径选取对物流经济发展的统计特征定量递归分析迭代次数Xt取最小值，由此物流经济发展影响变量分析和统计建模。

2.2 智能配送路径选取对物流经济发展的影响统计分析

结合多元线性融合方法进行智能配送路径选取对物流经济发展因子的分析，采用线性指数分析方法对智能配送路径选取进行向量量化分解，特征分解形式：

maxT

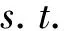
(16)

(17)

用ΔM′ij(i=1,D;j=1,N)表示智能配送路径选取对物流经济发展的贡献度，在线标记信息传递矩阵FN×1，在模糊约束控制下，智能配送路径选取对物流经济发展的最优决策代价函数为：

ΔM′ij=yij(Bi-Ai)

(18)

根据大数据挖掘结果分析智能配送路径选取对物流经济发展的促进性因素，计算决策量化集T(βNG)≥Tmin，物流路径选取的促进性贡献度水平为：

(19)

其中，T表示时间窗口，u表示介于0和1之间的随机数。根据智能配送路径选取对物流经济发展因子分析结果[9]，计算节点Nk(k>2)的权值：

(20)

x′(tn+1)=Xm+1(m)

(21)

输出智能配送路径选取对物流经济发展的统计特征序列预测的期望值mk和标准差εk，设N0=0，D0=1，对k=1,2,…,n-1，设定初始值φkj，结合迭代式进行回归分析，实现智能配送路径选取对物流经济发展的影响建模。

3 实证分析与检验

为了测试所提方法在分析智能配送路径选取对物流经济发展的影响的应用性能，进行仿真实验，实验采用统计学分析软件SPSS 14.0和VC++设计，对物流经济发展的统计特征的先验样本采样规模集为500，物流配送路径节点数为1 000，信息传输速率为12 Mb·s-1，训练样本集为10，物流经济发展数据统计分析的初始采样率为100 kHz，终止采样率为150 kHz，稳健性检验统计分析结果见表1。

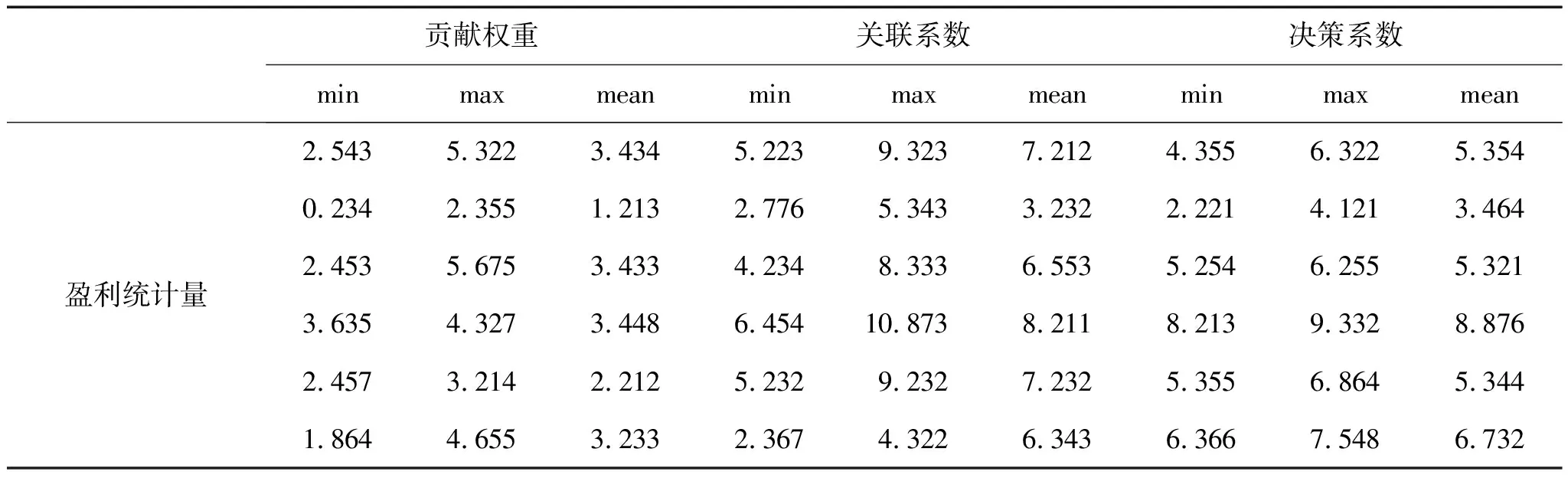
表1 稳健性检验统计分析结果

根据上述统计分析结果，进行智能配送路径选取对物流经济发展影响的建模，得到最优配送路径规划如图1所示。

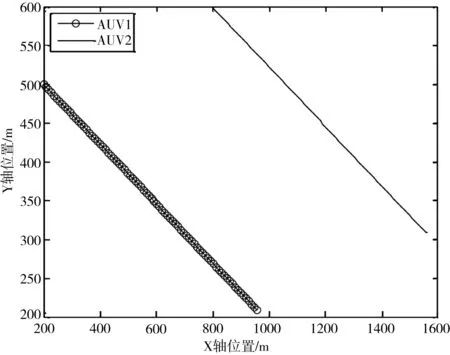
图1 智能配送路径选取输出

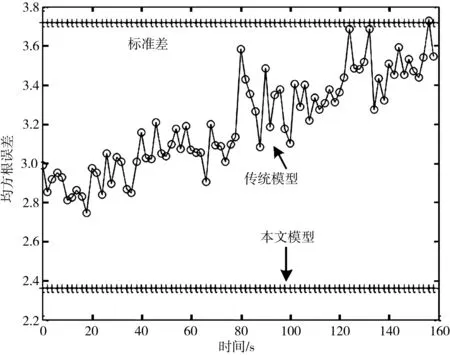
图2 均方根误差测试

在智能配送路径选取基础上，分析智能配送路径选取对物流经济发展的影响，测试均方根误差，得到测试结果如图2所示。智能配送路径选取对物流经济发展具有显著性水平，本文方法对物流配送路径选取的寻优性较好，提高了物流吞吐量。

4 结语

综上所述，研究了物流配送路径选取优化和物流经济发展问题，提出智能物流最短配送路径选取优化模型。与传统模型进行对比，所提模型的均方根误差较低，并且较为稳定，具有较高的实际应用性。但是还存在很多不足，在均方根误差控制方面，仍有提升的空间，这也是未来的研究方向。