毕达哥拉斯群决策方法及其在绿色供应商选取中的应用
2019-10-24施明华肖庆宪
施明华, 肖庆宪
(1.皖西学院 金融与数学学院,安徽 六安 237012; 2.上海理工大学 管理学院,上海 200093; 3.上海系统科学研究院,上海 200093)
0 引言
上世纪60年代,自动控制专家Zadeh定义了模糊集的系统化范式和计算法则,从而打开模糊集在决策分析领域的应用空间,使其成为表征不确定和模糊信息的一种主要工具。在日益复杂的决策环境下,人们对事物的认知结果往往呈现出肯定、否定和犹豫三个方面,而模糊集仅能通过隶属度刻画肯定信息。鉴于此,Atanassov对模糊集进行拓展,提出了直觉模糊集(IFS),用隶属度、非隶属度和犹豫度三个度量指标更细腻的度量信息。由于IFS在表征模糊和不确定信息时表现出灵活、高精度等特点,IFS被广泛的应用于供应链管理、电子商务推荐系统、数据挖掘、智慧医疗等诸多领域[1~3]。在IFS基础上,不确定性和模糊逻辑专家Yager提出一种新的模糊集,即毕达哥拉斯模糊集(PFS)[4],其理论框架完全不同于直觉模糊集。首先,二者的求补运算不同,IFS基于C(a)=1-a,而PFS基于C(a)=(1-a2)1/2。其次,IFS落脚点是满意度和非满意度值,而PFS采用类似极坐标系的方法,即基于满意度强度值和满意度方向偏离值来构建。构造方式的差异,使得二者的运算方式完全不同,并且PFS比IFS使用范围更广。因为前者限制条件较弱,要求隶属度和非隶属度的平方和不超过1,而后者限制条件较强,要求隶属度和非隶属度之和不超过1。目前,PFS已经引起诸多学者兴趣,并取得一些研究成果[5~7],但在管理决策领域的研究还处于起步阶段,相关理论有待进一步的完善和深入研究。
证据理论是一种非常实用的处理和表达不确定信息的技术手段,最早由Dempster在1967年提出,Shafer进一步给出其严格和规范化的定义。因此,证据理论又常被称为Dempster-Shafer理论,简称为D-S理论。证据理论将命题转化为集合的形式,利用信任度函数和似然度函数刻画命题的可靠性,并通过证据合成规则进行证据融合,从而进行决策。鉴于此,证据理论被视为一种依据证据做决策的理论,广泛的用于求解模糊决策问题。姚爽等人将证据理论和层次分析法相结合提出一种求解专家权重未知的模糊多属性群决策方法[8]。针对具有动态参考点以及混合型属性值的模糊多属性决策问题,靳留乾等人提出一种基于前景理论和证据理论的决策方法[9]。Dong Yuanxiang等人将证据理论和模糊软集相结合,提出一种新的模糊集合,即D-S模糊软集理论,并研究了D-S模糊软集环境下的多属性群决策问题[10]。针对权重未知且属性值为三角直觉模糊数的多属性决策问题,Li Xihua等人基于前景理论和证据理论提出一种新的决策方法[11]。但至今未见将证据理论应用于求解毕达哥拉斯模糊环境下的管理决策问题研究。
集结算子作为一种主要的信息融合工具,得到学者的广泛重视,产生了丰硕的研究成果。从关联性角度出发,集结算子可大致划分为两大类,一类认为集结变量间相互独立,代表性的有加权平均算子,几何平均算子,混合平均算子[3]。但在实际决策中,由于经济社会的复杂性,涉及的变量大都相互关联。鉴于此,很多学者提出通过利用变量间的交叉运算挖掘其关联信息,从而设计出另外一类基于交互运算的关联变量集结算子,代表性的有Heronian平均(HM)算子和Bonferroni平均(BM)算子[1,3]。但这些算子的交互运算是固定的,例如HM和BM算子均采用两两运算,当变量个数较多的时,挖掘关联信息的能力较弱。为此,Qin Jindong等人首次将MSM算子引入模糊信息的集结[12],其显著性的优势是可以根据决策情况自主设定交互运算变量的个数。目前,MSM算子已经被应用于犹豫模糊[13]、直觉不确定模糊语言[14]、单变量中智[15]、不确定模糊语言[16]等环境下的决策问题求解。然而,这些文献中涉及的加权MSM算子存在一个较大的缺陷,即不满足退化性和幂等性。为此,本文将对加权MSM算子进行重新设计,提出一种新的可退化并具有幂等性的混合加权MSM算子。
鉴于上述分析,针对属性值为毕达哥拉斯模糊数且专家权重未知的多属性群决策问题,本文构建了一种基于证据理论和加权MSM算子的群决策方法。该方法先利用决策矩阵间的距离,获取专家权重,在一定程度上解决了后期证据融合时的冲突问题。然后,再采用两种方法串行实施信息融合:第一阶段,针对存在关联关系的属性变量,用加权MSM算子进行集结,分别获得专家对各个候选对象的综合评价;第二阶段,针对各专家独立提供的综合评价信息,利用证据合成方法进行合成,获得各个候选对象的置信区间。最后,利用置信区间构建可能度矩阵进行优选决策。
1 证据理论
识别框架指的是某个命题的全部可能结果所组成的有限且完备的集合,通过识别框架的构建可将抽象的命题运算转化为集合运算。D-S理论的信任度函数、似然度函数和证据组合函数等重要概念均建立在识别框架基础之上。
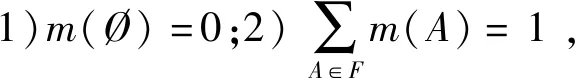
定义2[11]设F为D-S识别框架,F={F1,F2,…,Fn}为一组相互独立的结论所构成的集合,A和B为F子集。则A的信任度(Belief measure, Bel)函数和似然度(Plausibility measure, Pl)函数为
Bel(A)表示证据A一定发生的可信度;Pl(A)则表示证据A可能发生的可信度。显然,对于F的任意子集A都有Pl(A)≥Bel(A),故A的支撑度区间可表示为[Bel(A),Pl(A)],也称为A的信任区间。为了将多个证据信息进行融合,以便实施优选决策,Dempster提出了如下的正交和法则。
定理1[11]设m1,m2,…,mn是同一识别框架下的Mass函数,所对应的证据分别为A1,A2,…,Ap,则有
m(A)=m1(A1)⊕m2(A2)⊕…mn(An)
2 混合加权毕达哥拉斯MSM算子
2.1 毕达哥拉斯模糊集
定义3[6]设X是一给定论域,则X上的一个毕达哥拉斯模糊集A为A={
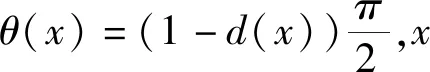
Zhang和Xu进一步提出毕达哥拉斯模糊数概念,即称二元数组α=P(μα,υα)为毕达哥拉斯模糊数,μα和υα满足约束条件(μα)2+(υα)2≤1,并给出如下的运算法则和二元关系,从而打开毕达哥拉斯模糊集的应用空间。
定义4[17]设αi=P(μαi,υαi)(i=1,2),α=P(μα,υα)是三个毕达哥拉斯模糊数,则有:

定义5[17]设α=P(μα,υα)为毕达哥拉斯模糊数,则α的得分函数为sα=(μα)2-(υα)2。对任意的两个毕达哥拉斯模糊数α1和α2,有如下的排序方案:
·若sα1>sα2,则α1>α2;
·若sα1=sα2,则α1=α2;
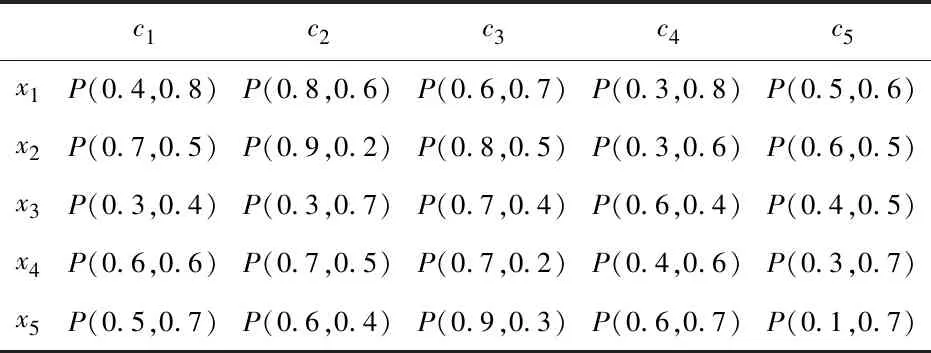
·若sα1 HWMSM(k)(a1,a2,…,an) 目前文献中常用的通过交互运算挖掘变量关联性的加权算子为:加权Heronian平均(WHM)算子[3]、加权Bonferroni平均(WBM)算子[3]和加权MSM算子,如表1所示改进后的HWMSM算子性质最为优良,并具有退化性、幂等性、有界性和单调性这些优良性质,下面我们将其推广到毕达哥拉斯模糊环境中并进行讨论。 表1 常用关联性算子比较 PFHWMSM(k)(α1,α2,…,αn) NWPFMSM(k)(a1,a2,…,an) OWPFMSM(k)(a1,a2,…,an) PFHWMSM(k)(α1,α2,…,αn) 据此可得 下证,由PFHWMSM算子得到的集结值也是毕达哥拉斯模糊数。显然有 综上定理得证。 定理3设αi=P(μαi,υαi),βi=P(μβi,υβi)(i=1,2,…,n)为毕达哥拉斯模糊数,若μαi≤μβi,υαi≥υβi(i=1,2,…,n),则PFHWMSMPFHWMSM(k)(α1,α2,…,αn)≤PFHWMSM(k)(β1,β2,…,βn)。 证明设PFHWMSM(α1,α2,…,αn)=ξ1=P(μξ1,υξ1),PFHWMSM(k)(β1,β2,…,βn)=ξ2=P(μξ2,υξ2),则有 即μξ1≤μξ2,类似可得υξ1≥υξ2,因此sξ1=(μ1)2-(υ1)2≤(μ2)2-(υ2)2=sξ2,由定义5可知PFHWMSM(k)(α1,α2,…,αn)≤PFHWMSM(k)(β1,β2,…,βn)。 定理4设αi=P(μαi,υαi)为一列毕达哥拉斯模糊数,若αi=α=P(μα,υα)(i=1,2,…,n),则PFHWMSM(k)(α1,α2,…,αn)=α。 证明PFHWMSM(k)(α1,α2,…,αn) 证明由定理3和4可得PFHWMSM(k)(α1,α2,…,αn)≤PFHWMSM(k)(α+,α+,…,α+)≤α+以及α-=PFHWMSM(α-,α-,…,α-)≤PFHWMSM(k)(α1,α2,…,αn),因此,可得α-≤PFHWMSM(k)(α1,α2,…,αn)≤α+。 随着参数k的变化,可得PFHWMSM算子的一些特例。 Case1若k=1,则PFHWMSM退化为毕达哥拉斯模糊混合加权(PFHWA)平均算子: PFHWMSM(k)(α1,α2,…,αn) =PFHWA(α1,α2,…,αn) 即将Liao等人定义的HWA算子[18]推广至毕达哥拉斯模糊环境。 PFHWMSM(2)(α1,α2,…,αn) =PFGWHM1,1(α1,α2,…,αn) 即将Liu等人定义的GWHM算子[19]推广至毕达哥拉斯模糊环境。 Case3若k=n,则PFHWMSM退化为毕达哥拉斯模糊几何(PFG)平均算子: PFHWMSM(n)(α1,α2,…,αn) =PFG(α1,α2,…,αn) 即将经典的几何平均算子[2]推广至毕达哥拉斯模糊环境。 i=1,2,…,n;k=1,2,…,l 步骤4针对每个专家关于方案的规范化综合评价信息,利用证据合成方法进行集结。 Mi(A)=m1i(A1)⊕m2i(A2)⊕…⊕mli(Al) 其中A,A1,A2,…,Al∈{accept,reject,(accept, reject)}。 步骤5给出候选方案Yi关于综合证据Mi的信任区间Ii,即Ii=[Bel(xi),Pl(xi)],并依据信任区间给出候选方案间的可能度矩阵P=(pij)n×n,其中pij表示候选方案Yi优于Yj的可能度,计算公式为 步骤6计算可能度矩阵P=(pij)n×n的排序向量{P1,P2,…,Pn},其中 依据Pi的大小对候选方案进行优选决策,Pi值越大则表示方案越好。 例1出行便捷、节约能源等优势使得电动自行车在我国得到极大的推广和应用,国家统计局公布数据显示,2016年我国电动自行车累计产量超过3000万。但电池一直是制约电动自行车发展的主要瓶颈,层次不齐的质量导致电池较高的淘汰率。废旧电池不妥善处理会溢出含铅重金属和酸性物质,从而对环境造成极大危害。因此,为电动自行车制造商寻求绿色电池供应商尤为重要。某品牌电动自行车公司有五个可供选择的电池货源,为选择出最佳绿色供应商,该公司结合自身情况制定了五个评价指标:产品质量(g1)、使用环境友好型的材料与生产技术(g2)、创新能力(g3)、服务水平(g4)、产品价格(g5),其权重向量为w=(0.2,0.4,0.1,0.1,0.2),同时公司用权重λ=(0.3,0.25,0.2,0.15,0.1)来体现其对电池货源突出属性的偏好。为达到公平合理的决策结果,公司决定聘请三名业内专家Di(i=1,2,3)对五家供应商进行评价,专家所提供的决策矩阵如下: 表2 毕达哥拉斯决策矩阵H(1) 表3 毕达哥拉斯决策矩阵H(2) 表4 毕达哥拉斯决策矩阵H(3) 下面用本文的决策方法,为该公司选出最佳绿色供应商。 步骤2利用评价矩阵间的距离,得出决策专家的模糊测度,进而确定其权重系数,具体计算结果如表5所示。 表5 权重系数求解结果 表6 综合评价信息 步骤3计算属性的得分值并进行排序,然后利用PFHWMSM算子对专家Dk关于各个方案Yi的属性评价信息集结,得到专家Dk关于Yi的综合评价信息,具体如表6所示。 步骤4将方案的综合评价信息规范化,并利用证据合成方法合成,得到每个备选方案的综合证据信息,计算结果如表7所示。 表7 证据合成结果 步骤5由备选方案的综合证据信息,可知各方案的信任区间分别为I1=[0.076,0.090],I2=[0.187,0.246],I1=[0.117,0.161],I1=[0.098,0.133],I1=[0.145,0.181]。据此,可得候选方案间的可能度矩阵P=(pij)5×5。 步骤6由可能度矩阵的排序向量{0.075,0.275,0.175,0.135,0.215},可得候选方案的排序为x2>x5>x3>x4>x1,因此最佳绿色供应商应为x2。 毕达哥拉斯模糊集的理论研究尚处于起步阶段,用于多属性群决策的方法不多见,这里我们选取文献[20]的方法和本文方法进行比对。文献[20]利用专家提供的决策矩阵和理想矩阵间的相似度分配专家相应的权重,再利用毕达哥拉斯加权平均(PFWA)算子进行集成。尽管两种方法都基于决策矩阵挖掘权重信息,但两者有一定的区别,文献[20]以全体决策矩阵的算术平均矩阵作为参照点,从而获取专家权重,这难免会造成决策信息的丢失或者扭曲,而本文完全基于原始数据直接进行挖掘,更加真实客观。在决策信息融合的方面二者也有区别,文献[20]在属性信息融合和专家信息融合两个阶段均采用PFWA算子,而本文方法则表现的更为细腻,在两个阶段分别利用PFHWMSM算子和证据合成方法进行融合。 表8 文献[20]计算结果 表8可见,两种方法给出的排序结果完全一致,均认为x2为最佳商业合作伙伴,这说明了本文方法的可行性。进一步分析可能度排序向量和得分值排序向量,可见文献[20]明显放大了候选方案间的差异。这主要基于以下原因:首先,本文所使用的PFHWMSM算子考虑了变量间的联系,事实上管理决策实际问题研究中所涉及的变量都或多或少存在关联性,但PFWA算子认为属性变量间相互独立;其次,本文利用证据理论来集成专家间的信息更符合人类的思维方式,能比集结算子更有效的处理不确定模糊信息[9,21,22];最后,文献[20]的信息集结方法没有反映出候选方案针对不同的因素有所侧重的特点,例如有的电池侧重于使用绿色生产材料但价格偏高,有的则侧重于电池使用年限但服务水平略逊一些,忽略这些信息以至于产品间的差异被放大。 针对属性值为毕达哥拉斯模糊数并且专家权重未知的多属性群决策问题,本文提出一种基于证据理论和混合加权毕达哥拉斯MSM算子的群决策方法。新方法以多数人的意见为出发点,挖掘原始数据信息,设计出一种确定专家权重的方法;然后,再采用混合加权MSM算子对候选变量属性信息进行集成,所采用的新算子一方面比传统的加权MSM算子性质优良,满足退化性、幂等性等性质,并且是常见的混合加权平均算子、GWHM算子、几何平均算子的广义形式,另一方面比Bonferroni平均等算子在捕获变量k间的关联性方面更灵活,通过参变量k的设置自由选取交叉运算变量的个数;最后,将专家的综合评价信息看成证据,进行D-S证据集结,得到综合证据信息,并进行优选决策。但该方法也有不足之处,对于属性权重未知,以及属性值为区间值的情形没有加以讨论,下一步的研究重点将是讨论属性权重未知、属性值为区间毕达哥拉斯模糊数的群决策问题。2.2 混合加权迈克劳林对称平均算子
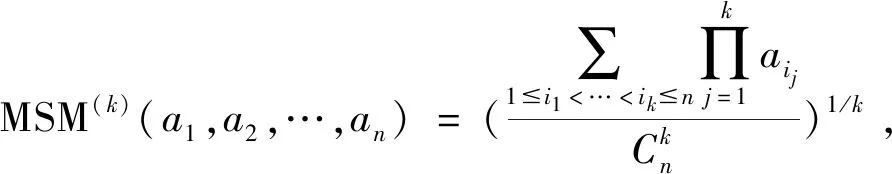
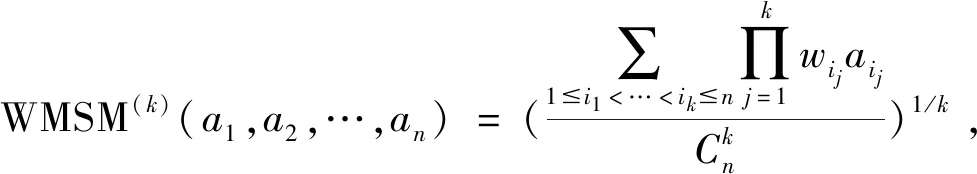

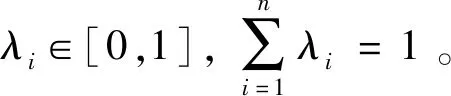

2.3 PFHWMSM算子
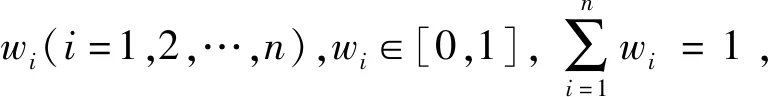
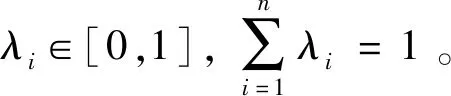
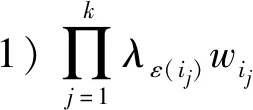
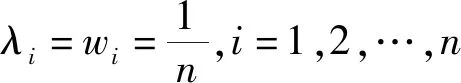
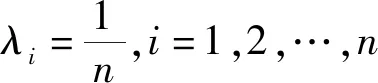


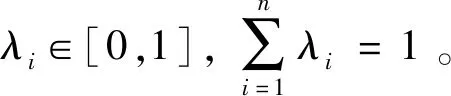
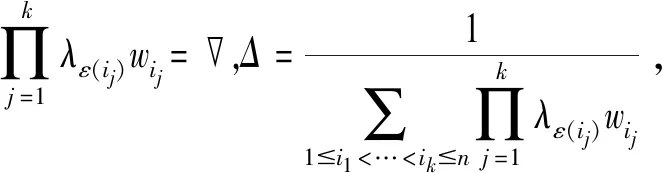

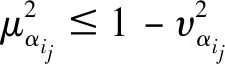


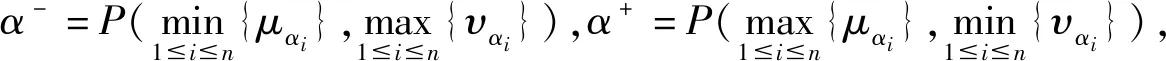
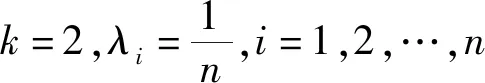
3 毕达哥拉斯模糊多属性群决策方法

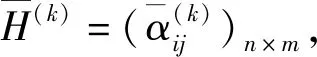
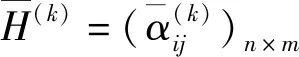
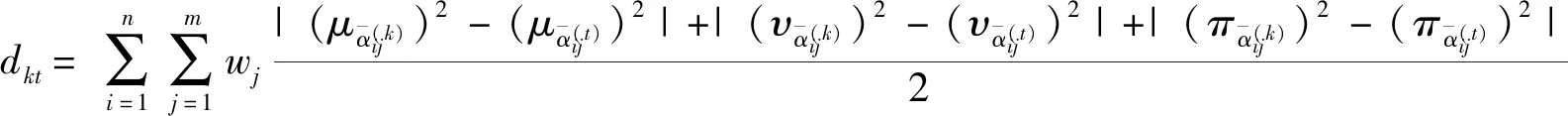
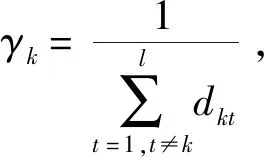





4 实例分析

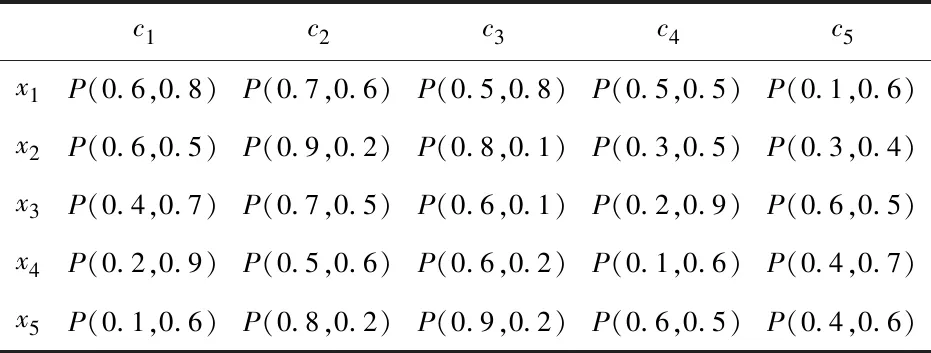
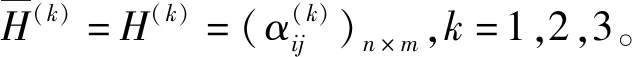

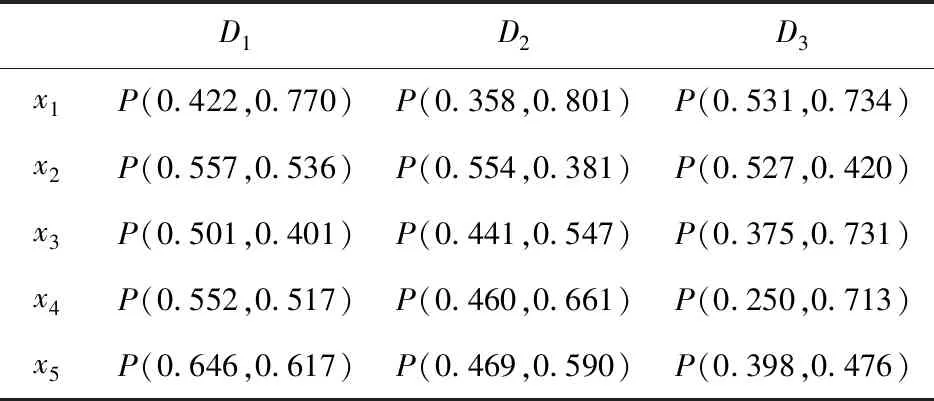

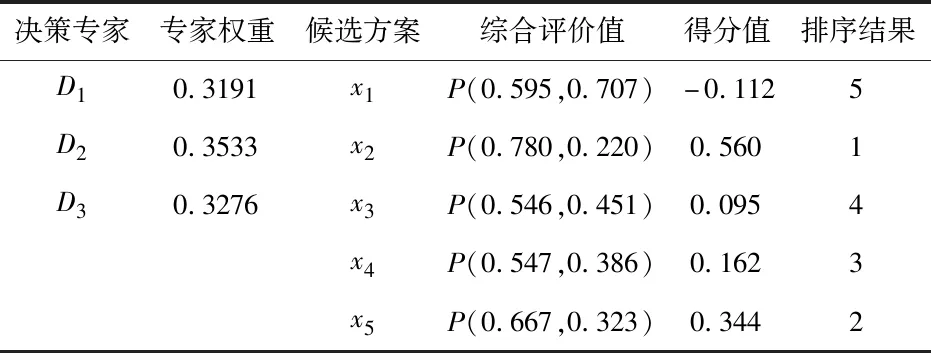
5 方法比较与讨论
6 结论
