ICOMDT:一个面向动态任务的交互计算模型*

李念龙,黄 进,田 丰,戴国忠,王宏安

1(人机交互北京市重点实验室(中国科学院 软件研究所),北京 100190)

2(中国科学院大学 计算机与控制学院,北京 100190)

1 概述

随着交互式多媒体技术的发展,计算机呈现给用户的信息变得越来越丰富,动态形式的交互任务也变得越来越普遍.比如,在航班管理系统中,用户需要选择飞行中的航班,查看有关该航班的详细信息;在虚拟射击游戏中,射击识别系统作为核心部分对用户体验有着至关重要的影响[1].然而,相比于静态形式的交互任务,如Windows 操作系统中的菜单选择,动态交互任务无疑会给用户带来更大的挑战.用户需要不停地接受和处理动态任务信息,认知负荷随之增加.此外,用户在交互过程中还需要保持高度集中的注意力,控制肌肉运动与感知神经的协调一致[2].这些因素给用户与界面的交互行为引入了噪音干扰,使得用户最终输出的信息并不一定是实际所想.例如,当用户点击快速移动的目标时,经常会点偏或点错[3,4].但对计算机而言,用户行为的内部产生过程是一个黑盒,计算机只能观测到用户最终的输入,并将此作为唯一的用户意图判断依据.从而导致用户与动态任务的交互效率低下,常常需要花费更多的时间并且很容易产生疲劳.

可见,为了提高用户与动态任务的交互效率,对用户行为的内部产生过程建模,进而实现用户行为的意图理解,对包含动态内容的用户界面有重要意义.运动目标获取任务[5-7]是动态用户界面中最为基础和广泛使用的交互任务.研究者们已经对用户在这项交互任务中的感知过程、认知过程与运动表现进行了大量的研究.在用户对运动物体的感知过程中,主要包括物体位置变化、物体的运动速度以及物体的运动方向[2].研究表明,这3种感知是相互独立的[8-11].在Brouwer 等人的研究中还发现,用户在动态交互任务中使用的并不是感知速度,而是基于经验记忆的平均速度[8].尽管这些结论可以很好地解释用户在动态选择任务中的一些表现,但却没有形成一套完成的模型框架,并且也没有应用在计算机对用户的意图理解上.在对用户的认知研究方面,ACT-R 模型描述了一个较为完善的用户认知与外界环境的交互模型[12].用户在认知过程中,除了整合外界的感知信息以外,还需要从目标意图与记忆存储中提取相关的内容.此外,贝叶斯方法作为一种可计算的模型,被广泛应用在计算机对用户的认知分析中.在Körding 等人的研究中,通过贝叶斯方法推断用户真实的感知信息[13],使计算机能够分析用户的认知,但是他们并没有对用户意图进行理解.在对用户的运动研究方面,许多与空间约束任务相关的模型和优化方法被提了出来,如随机优化子运动模型[14]和统计校准法[15]等.这些模型虽然能够对用户的表现建模,但却面向静态交互任务,并且缺乏完整的用户交互模型框架分析.

本文提出的ICOMDT(interaction computational model for dynamic task),是一个面向动态交互任务的定量化可计算的交互模型.该模型融合了已有研究的成果与思想,将用户与计算机的交互过程进行分解并统一建模,它由用户模型中的感知模型、认知模型、运动模型、目标意图和记忆存储模块以及计算机模型中与之对应的动态任务、认知解码、交互设备、意图理解和数据模型共10 个模块组成.计算机能够根据动态任务的先验信息、用户的输入信息结合数据模型对用户认知进行解码,进而得到用户的目标意图.通过该模型可以辅助计算机更好地理解用户意图,提高用户与动态任务的交互效率.

更具体地,我们将该模型在运动目标获取任务中加以应用,对用户点击运动目标的落点分布建立高斯分布数据模型,并使用贝叶斯方法推断用户的意图目标.为了验证模型的有效性,我们设计了与两个运动目标选择任务相关的实验.实验1 首先对用户数据模型进行拟合,并用于预测用户选择的错误率.实验2 根据动态交互计算模型实现了一种辅助运动目标选择技术,使用实验1 中拟合的数据模型,能够有效地缩短用户的目标选择时间,并提高目标选择的准确率.

本文的贡献主要有以下几点.

(1)提出一个面向动态任务的交互计算模型——ICOMDT,用于解释用户与动态任务的交互行为并实现用户意图预测.

(2)将ICOMDT应用于运动目标选择任务,提出一套可计算的模型方法,能够根据任务参数预测用户目标选择的错误率.

(3)基于ICOMDT实现一种辅助运动目标选择技术,能够有效地缩短运动目标的选择时间并提高选择的准确率.

2 相关研究

为了将用户与计算机的交互过程进行分解并统一建模,我们在感知模型、认知模型以及运动模型3 个方面对已有工作进行了归纳,下面分别对这几个方面展开阐述.

2.1 用户感知研究

用户对运动物体的感知主要包括物体位置变化、物体的运动速度以及物体的运动方向[8].虽然物体的运动速度与位置随时间的变化有关,但研究表明,用户对物体运动速度的感知并不依赖于位置感知变化[9].在Brenner等人的研究中也将用户对速度感知转化为对时间的感知[11],并影响用户选择目标的时刻.具体来说,如果用户预估速度偏小,会导致选取目标的时刻提早;而用户预估速度偏大,则会导致目标的选取时刻滞后.运动方向的感知也被证实不受物体位置感知变化的影响[16,17].然而,对物体运动速度感知和运动方向感知之间的关系的研究却存在一些争议[18,19].仅就运动目标获取任务而言,Brouwer 等人在2003 年通过实验证实了用户对物体速度和运动方向的感知是相互独立的[8],这个结论为我们构建ICOMDT提供了重要依据.

在Brouwer 等人的实验中,用户被要求用一根有机玻璃棒在显示屏上点选朝特定方向以恒定速度运动的目标.实验通过控制目标是否在移动过程中消失以及背景的运动来探究运动方向感知对用户选择目标的影响.结果表明,无论目标是否在移动过程中消失,用户选择目标时的落点误差距离无显著性差异,但是背景运动却会影响落点的误差距离(背景运动影响了用户对目标运动方向的感知).因此,用户动态任务交互过程中用到的是实际感知到的运动方向而不是基于经验预期的方向;相反地,对运动速度用到的是基于经验预期的平均速度而不是感知到的速度,根据实验结果发现,用户在选择运动速度较慢的目标时距离偏移更大;在选择速度较快的目标时距离偏移更小.因此,Brouwer 等人认为,用户在动态交互任务中,对运动速度的感知和运动方向的感知是分离的.这表明,物体的运动(速度)不能在不同方向上分解.

综上所述我们认为,在动态交互任务中,用户对运动物体的位置变化感知、运动速度感知以及运动方向感知都是相互独立的.尽管研究者们已经尝试通过实验来分析用户在一些简单动态交互任务中的感知状态,但却没有提出一套完整的交互理论模型,并且也未能使计算机对用户意图进行理解.

2.2 用户认知研究

近年来,研究者们对用户认知科学的研究已经不仅限于感知觉、言语过程、思维过程等传统的认知机能,许多新型研究领域,如认知神经计算、社会认知决策的出现,让很多不同行业的人都开始从事与认知研究相关的工作,许多模型方法也被研究者们提了出来.

2.2.1 认知模型

思维理性的自适应控制(adaptive control of thought-rational,简称ACT-R)已经发展成为由多个模块组成的理论[12],常用来解释人类与外界环境交互时的认知过程.该模型主要包含4 个模块和1 个中央控制系统,4 个模块分别是:用来识别视野范围内的物体的视觉模块(visual module)、控制手部运动的操作模块(manual module)、从记忆内存中检索信息的声明模块(declarative module)以及追踪当前目标和意图的目标模块(goal module).ACT-R 已被证实通过这4 个模块与中央控制系统的交互过程及所需的时间损耗,能够对文本输入时间[20]、错误率[21]和视觉搜索策略[22]等用户行为进行准确预测.虽然ACT-R 仅对用户认知加工过程进行了解释,无法辅助计算机对用户行为进行意图理解,本文创造性地将意图理解过程看作是认知加工过程的近似逆过程,并将其用于ICOMDT意图理解归因体系的构建当中.

2.2.2 认知推理

认知推理是人类结合感知刺激与记忆形成对外部环境认识的过程,虽然是否存在规范性描述人类认知推理过程的机制存在争议,但简单的统计推断法却已在这些方面得到多方证实[23,24].这种方法即贝叶斯法则,它在描述用户将当前观察到的信息和先验记忆中的信息结合的行为中非常成功,为我们提供了一个操作性很强的理论框架,描述用户对事件进行感知推理的过程[23].Körding 等人指出,实际上环境中的对象具有很强的统计规律性,且人类大脑对这种规律有着很强的学习能力,使人脑在特定环境中对外界线索的感知能够被概率统计模型所描述,他们用实验证实了贝叶斯模型能够很好地描述这种学习能力[13].Lu 等人也通过贝叶斯方法描述了在多通道信息融合的交互模型中,人们如何根据感知层传来的信息进行决策[25].虽然他们只是针对感知任务进行用户意图理解,但却为在动态交互任务中解码用户意图,进而实现计算机意图理解提供了重要依据.

2.3 用户运动研究

Fitts 定律作为著名的用户表现模型,描述了空间约束运动任务中速度与准确性的关系,并能够预测用户的平均移动时间[26,27].确定性迭代修正模型进一步解释了用户从初始位置到目标区域的总体移动包括一系列离散的子运动[28,29].基于确定性迭代修正模型,Meyer 等人提出随机优化子运动模型[14],并对子运动分量落点分布的标准差进行了分析:对于主要子运动和次要子运动,用户落点分布的标准差均与用户移动的平均速度成正比,在移动距离固定的情况下与运动时间成反比.

Meyer 的研究虽然分析了用户在空间约束任务中最终落点分布的影响因素,但却只是针对用户运动的影响进行了分析.2013 年,Bi 和Zhai 提出了一种通过建立统计校准模型解决用户在触摸屏上选择静态图标精准度的方法[15].该模型认为用户点击目标的落点分布服从正态分布,均值为一个常数,与设备本身的精准度有关;方差除了受设备本身精准度的影响外,也与目标的大小有关.尽管Bi和Zhai的研究是对用户操作整体建模,最终的落点分布也仅与初始任务参数有关,但在他们的研究中目标是静止的,并且他们所建立的模型并没有分析用户的感知和认知过程.

研究者们还将最优化模型应用于解释用户与动态任务的交互运动.其中,主要包括开环(open-loop)和闭环(closed-loop)两类模型.在开环控制模型中,最优化的目标集中获得最合理的肌肉活动[30,31]、关节力矩[32]或者上肢姿态[33,34],而忽略了在线的感知反馈,并且经常把人类运动看作是一个预先确定的动态系统.相比开环控制系统,闭环系统采用了更加类似人类的处理模式,这种模式不再依赖于提前预知的期望轨迹(desired trajectory),而是能够在不可预测的波动下反复再现[35].尽管闭环控制系统与人类运动的相似度更高,但在实际设计中很难直接使用这些模型,因为需要对参数进行高精度的计算优化.

3 动态交互计算模型

为了将用户与计算机的交互过程进行分解并统一建模,实现动态交互任务中用户意图的准确理解,我们提出ICOMDT,其体系结构如图1 所示.它与以往意图理解模型的主要区别在于,以往方法中用户与动态任务交互是以一种黑盒的方式进行,即计算机不知道用户在接收信息后会如何操作,无法理解用户的意图.由于用户自身复杂的生理结构,神经冲动信号在传递至肌肉运动的过程中难免会伴随有干扰噪音,导致最终的行为输出与用户意图产生偏差.如果仅以用户的输出作为唯一依据,计算机很容易做出一些错误的判断,带来不必要的交互耗时与不友好的交互方式.

在ICOMDT中,我们将交互过程划分为用户空间和计算空间两个部分,在用户空间中,主要参考了ACT-R 模型[12]对用户认知这一黑盒过程进行了模块划分,并基于对用户感知、认知和运动表现的已有研究,分析了用户与动态任务的交互过程,在计算空间中,通过对认知空间进行近似的逆向建模,实现用户在动态交互任务中的意图理解,进而提高交互效率.下面我们首先对ICOMDT的体系结构进行介绍,然后再给出一个应用于运动目标获取用户表现建模的例子,以说明其工作过程.

3.1 ICOMDT体系结构

(1)感知模型:用户通过感觉器官接收计算机传入的动态任务信息.主要为视觉信息感知,也可能包含听觉信息或触觉信息等多通道信息感知.

(2)认知模型:用户在大脑皮层对感知到的信息进行加工整合处理,理解动态任务并做出相应决断,之后激活额叶中央前回运动区产生运动信号.

(3)运动模型:当运动信号下传至脊髓,激活脊髓前角元运动细胞后,肌肉就开始运动,完成我们所期望的操作,这是用户的信息输出模块.

(4)目标意图与记忆存储:根据ACT-R 模型[12],用户在认知层面处理时,需要追踪当前的目标意图并从记忆存储中提取有效的经验信息指导当前操作,这一过程即对应于目标意图与记忆存储模块.

(5)输出设备:与用户的运动模型相对应,是计算机的信息输出模块,可以包括视觉呈现、听觉呈现、触觉呈现等多种形式.

(6)认知解码:计算机对用户认知过程的解析,是用户内部处理过程的近似建模.

(7)输入设备:与用户感知模型相对应,是计算机的信息输入模块,可以包括手指、鼠标以及操纵杆等交互输入设备.

(8)意图理解与数据模型:两个模块相辅相成,它们都必须结合认知解码模块工作.当认知解码模块以用户操作为输入时,可利用意图理解模块反向推测出用户意图;当认知解码模块以交互任务参数为输入、输入设备传入数据为标签时,可实现模型训练,并将训练好的模型和参数在数据模型模块进行存储.

(9)认知交互任务与计算交互任务:ICOMDT与具体交互任务进行适配的模块,在用户空间中,这个模块以人类意识的形式存在,它意味着用户大脑当前对特定任务的认识以及以往执行任务留下的记忆,根据ACT-R模型[12],它为用户的目标意图、记忆存储模块提供识别任务目标并执行相应的操作的认知和记忆;在计算空间中,这个模块以计算逻辑和参数的形式存在,它不仅规定了具体任务的交互界面和内部逻辑,还为用户数据模型的构建和意图理解提供规则和参数支撑.

在一次交互过程中,计算交互任务首先指导计算机将界面内容呈现给用户,用户通过感知模型对任务内容进行感知,之后在认知模型中对感知到的信息加工整合理解,用户通过之前对该交互任务直接或间接的了解,已经形成了经验和认识,并存放于认知交互任务模块中,在这些经验和认识的作用下,目标意图模块明确任务中需要完成的目标,并在记忆存储模块结合经验知识对当前任务做出决策,最后将控制信号传递至运动模型,控制肌肉运动完成期望行为操作.

用户行为通过输入设备进入计算机,传递至认知解码模块,同时交互任务的相关信息作为计算机的先验知识也通过数据模型传入认知解码模块,计算机根据二者的信息并结合已经建立的数据模型对用户认知进行反向解码,推断用户的目标意图,通过意图理解模块反馈给交互任务,最后交互任务将结果重新呈现给用户,完成一次交互.

3.2 运动目标选择任务

下面我们将ICOMDT应用于运动目标获取任务中,对其用户表现,或者更具体地说,对运动目标选择的落点位置(endpoint)进行建模.我们将根据ICOMDT体系结构对各个模块的具体内容分别加以介绍.

3.2.1 计算交互任务运动目标获取任务的定义如下:电脑屏幕中有单个或多个运动的圆形目标,用户需要尽可能快速并且准确地使用鼠标选中其中一个目标.

研究表明,在静态交互任务中,用户会最大限度地利用目标宽度来节省他们选择目标的时间[36],我们相信,该发现在动态交互任务中也同样存在.而在运动控制理论中,感知-运动控制系统存在时间延迟,这可能导致终点落后于目标[37],当目标移动速度更快时,这种趋势变得更强.因此,我们把目标的运动速度(V)和大小或直径(W)作为任务相关参数,并且这两个任务参数作为先验信息是已知的.在这个案例中,我们采用图形显示器作为输出设备,采用鼠标作为输入设备,用户的输入行为就是按下鼠标按钮时鼠标的位置.

3.2.2 认知解码

根据动态交互计算模型,推断用户意图的方法为用户认知和运动行为的逆向推理,因此,在这一模块中,我们首先需要将用户的认知和运动处理过程进行有效的近似建模.从用户的角度来看,用户最初得到的刺激为任务呈现,从上一节可知,在运动目标获取任务中,最重要的信息即为运动目标的V与W,而用户最终的输出为选择落点,因此,这个近似建模过程即找到任务参数V和W与选择落点之间关系的过程.

考虑到人类本身复杂的生理结构,我们很难用计算机模拟出用户的整个认知处理过程.此外,由于从用户大脑发出指令到最终按下选择按钮几乎是在很短时间内完成的,我们可以认为用户每一次操作都是开环控制,即从用户感知到最终输出之间不存在反馈回路.因此,为了简化计算,我们利用数据驱动[38,39]的方法找到任务参数与落点之间的一个开环函数,以此表示它们之间的关系.更近一步地,大量研究表明,用户在静止目标选择任务中的落点分布服从正态分布[36,40,41],我们假设运动在运动目标选择中的落点样本总体X服从正态分布,那么任务参数与落点之间的关系则可以转变为V和W与正态分布均值和协方差之间的关系,如图2 所示.

1)速度大小与运动方向分解

Brouwer 等人指出,目标速度大小与运动方向在被用户感知时是相互独立的[8],我们以目标中心为原点建立坐标系:定义x方向为目标运动方向,y方向为与目标运动方向垂直的方向,由此可得,x方向上的移动速度为V,y方向上的移动速度为0,两个方向上的目标大小均为W.在此坐标系下,x方向的偏差体现了运动速度变化对用户落点的影响,y方向的偏差体现了空间方向变化对用户落点的影响,两个方向上的影响相互独立.因此有:

接下来,我们通过分析动态交互计算模型建立任务参数(V,W)与正态分布参数(μx,μy,σx,σy)之间的关系.

2)V对μx和σx的影响

用户落点在x方向上的分布主要是由速度变化引起的.在Brenner 等人对移动目标捕获问题的研究中[11],物体实际运动速度与用户感知速度的差异会导致用户最终选择目标的位置提前或者滞后.

假设用户预估速度为ve,那么目标最终在t时刻被预测选中的位置xe为

其中,delay表示视觉信息转化为肌肉刺激的延迟时间,te是预估的选中目标的时刻.而实际选中目标的位置xa可以被写作:

其中,ta是目标实际被选中的时刻,va也是目标的实际速度.为了准确选中目标,用户预估的位置应该与实际位置相同(i.e.xe(t)=xa(t),t=ta).所以,合并公式(3)和公式(4)后可得:

因此,如果用户估计的速度偏小,会导致选取目标的时刻提早,落点位置提前;而如果用户预估速度偏大,则会导致目标的选取时刻延迟,落点位置滞后.我们将V对μx产生的影响近似地用线性关系式表示:

根据随机最优化子运动模型[14],用户的选择速度会影响落点分布的标准差,对主要子运动有:

其中,V1是主要子运动的平均速度,D1和T1分别是主要子运动的平均距离和平均时间,K为常量系数(K>0).如果主要子运动错过了目标区域,并且在与目标中心点Δ距离范围内结束(Δ≥W/2),根据模型将会有次要子运动在T2Δ的时间里移动Δ的距离,最终的落点分布的标准差为S2,即有

而运动目标的速度显然会影响用户的选择速度,进而影响选择落点的不确定程度,因此,我们近似地认为σx正比于V.

3)V对μy和σy的影响

用户落点在y方向上的分布主要是由空间方向感知误差引起的.用户对运动方向感知不受感知速度的影响[8],因此,μy不受V的影响,即:

然而,用户的选择速度依然受到目标移动速度的影响[42,43],根据随机最优化子运动模型的公式(9),V仍会对σy产生影响.这也符合常理,目标移动速度越快,用户就要越迅速地移动鼠标追逐选择目标,尽管落点分布的均值趋于中心,但是不确定性却会随之增大.

4)W对μx和σx的影响

对于静止目标选择任务,Bi 和Zhai 研究发现,W会影响落点分布的标准差,但并不影响均值[41].

其中,σa为常数,表示设备的绝对精度,常数c表示绝对偏移度,通常情况下设为0.但在运动目标选择任务中,由于x方向上目标运动速度的干扰,用户会尽可能地利用W,或者说目标本身对运动精度的容忍度[36],以抵消速度V带来的影响.换句话说,一般情况下,目标的移动会造成用户的点击落点滞后,而用户会尽可能地通过预判弥补滞后偏差,目标越大,这种弥补就会变得越明显.因此,暂且先把绝对精度抛掉.同样,我们将W对μx和σx的关系近似地看作正比关系:

5)W对μy和σy的影响

由于y方向没有速度分量的存在,用户不必要利用W以抵消速度V带来的影响,所以,我们可以认为W对落点分布的影响与静止目标选择任务类似,根据公式(12),将μy设为0:

同时,由于目标为圆形,在y方向上目标大小仍为W,因此,W对σy的影响与x方向保持一致.

6)总落点分布函数

为了得到最终的正态分布函数,需要将上述V和W对落点分布产生的影响进行叠加.我们将这种影响表示为与V和W有关的两个正态分布和此外,再引入一个正态分布表示绝对精度[41],它们形成了总体分布的3 个子分布,利用正态分布相加仍是正态分布的规则,我们便可以通过加法运算得到最终的总体分布.

根据公式(6)、公式(9)～公式(11),V产生的子分布可以写为

其中,bx,ex,ey均为常数.

根据公式(14)～公式(17),W产生的子分布可以写为

其中,cx,cw,x,fx,fy均为常数.

绝对精度产生的正态分布均值和协方差均为常数.

根据精度容忍度理论[36],当W越大时,V的作用越小,因此,假设Xv和Xw相互之间不独立,且它们的协方差为

其中,gx,gy为常数,V2/W2这一项体现了目标大小对目标速度的抑制作用.

最后,利用二维正态分布的线性组合仍是正态分布的性质,将上述3 个正态分布相加即可得到总体正态分布表达式:

3.2.3 数据模型

从前面的章节可知,数据模型模块实际上是实现了认知解码模型,即公式(23)的训练和存储.其训练过程包括两个步骤:(1)收集用户在不同V和W下选择目标的落点数据;(2)利用认知解码模型对收集到的数据进行拟合,完成模型参数的估计.我们将在后面的实验章节中对这部分内容进行详细介绍.

3.2.4 意图理解

在认知解码过程中,我们选择使用贝叶斯法则实现认知过程的逆向推理.假设有n个候选目标T={t1,t2,…,tn},若用户点击选择的落点为s,那么目标t是用户意图目标的条件概率为P(t|s).要想找到这个意图目标就等同于寻找目标t*使P(t|s)的概率最大,根据贝叶斯定理,可以得到:

其中,P(t)为先验概率,假设每个目标初始情况下被选中的概率相同(即为1/n).P(s|t)为似然函数,用以描述用户在s点欲选择t目标的概率.P(s)为正则化系数,所有目标取值相同.因此,我们寻找t*使P(t|s)最大就等同于使P(s|t)最大,即:

注意到每个运动目标都有唯一的W和V,通过训练好的数据模型计算特定V和W目标的落点分布,就能够根据当前落点s反推出其属于该目标t的概率P(s|t),进而可以得到用户的意图目标t*.

4 实 验

为了验证动态交互计算模型框架的有效性,我们设计了两个基于运动目标选择任务的实验.

4.1 实验1:模型拟合与错误率预测

在本实验中,我们通过收集用户点击落点数据来拟合数据模型参数,并对任务中的点击错误率进行预测.

4.1.1 参与者及实验环境

我们招募了12 名人员参与实验,男女各6 名,平均年龄25 岁.他们的惯用手均为右手,平时也都有使用计算机的习惯.

实验在联想P318 的电脑上进行,采用2.6GHz Intel Core i7 CPU 以及分辨率为1920×1080 的23 英吋(533.2×312mm)LED 显示器,交互输入设备为戴尔MS111 鼠标(1 000dpi).实验界面程序使用C#代码编写.

4.1.2 实验设计与过程

实验采用组内设计,包含4 种目标大小W(24、48、96、144 像素)×4 种目标运动速度V(96、192、288、384像素/秒)共16 种情况.每种情况下测试者需要完成10 次选择操作,因此我们最终可以得到16×10×12 共1 920次点击数据.在实验过程中允许测试者休息.

在每一次的操作中,测试者点击屏幕中心的“开始”按钮开始实验.在等待很短的时间间隔后(大约700ms～2000ms),屏幕中会在随机位置出现一个朝随机方向运动的目标,测试者需要尽可能快并且准确地选中目标.每一次操作只允许点击一次鼠标按钮,无论有没有选中目标,我们都会记录点击的落点位置并进入下一次操作.

4.1.3 模型拟合

在使用模型对用户数据进行拟合的过程中,我们使用最小二乘回归方法(least square regression)对正态分布的参数μx、σx和σy进行估计,将参数μy设为0,因为实验数据显示,落点均值在y方向上的偏差几乎没有,设为0 后它的平均绝对误差(mean absolute error)为1.05 像素,表明它与真实数据非常接近.总体来说,我们的模型能够很好地拟合用户数据,对应的R2结果分别为0.961、0.938 和0.955.最终得到的数据模型参数系数见表1.

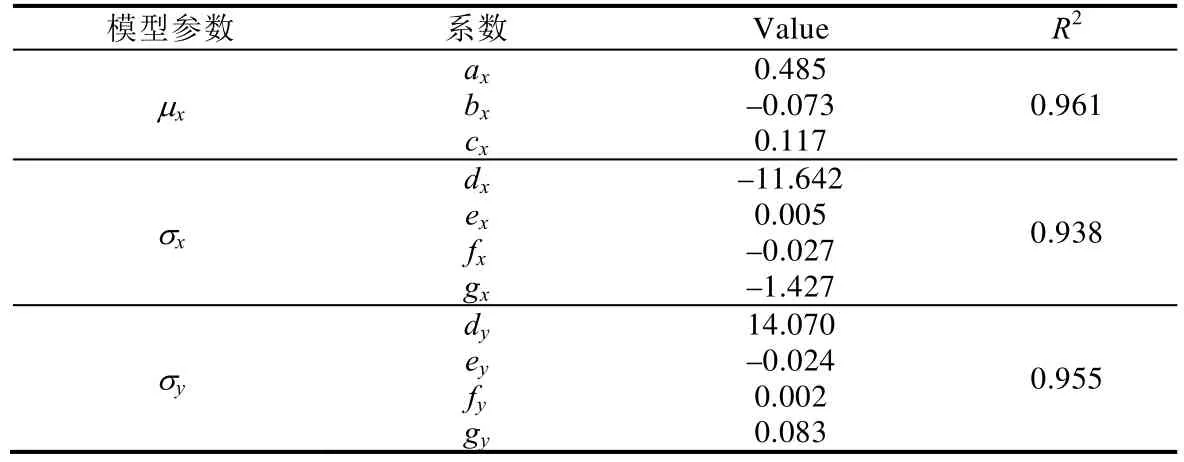
Table 1 Coefficient fitting results of normal distribution model表1 正态分布模型系数拟合结果

4.1.4 错误率预测

错误率是人机交互中最为重要的因素之一,已被广泛地应用于文本输入和计算机游戏等各种交互场景当中[44,45].在运动目标选择任务中,错误率被定义为错误点击次数占总点击次数的百分比,对于计算机原本的选择技术而言,用户点击的落点在目标外即认为是一次错误的点击.根据交互计算模型,只要给定动态任务参数W和V,就可以通过二维正态分布的累积分布函数(cumulative distribution function)计算落在目标区域外的概率,这一数值即为用户在该任务下的错误率.

不同目标大小和目标速度下的实际错误率与预测错误率结果如图3 所示,最小二乘回归得到R2值为0.995,表明我们的预测模型能够很好地预测任务错误率.

从图3 可以看出,用户的错误率随着目标运动速度的增大而增加,随着目标大小的增大而减小.这一结果也蕴含于数据模型中:x方向落点均值随着V的增大而向目标移动的反方向偏移,导致错误率的增加,而随着W的增大,这一效应得到抑制,因此在W较大的情况下(W=144 和W=96),错误率随速度增大而变大的斜率是较小的.x和y方向落点方差随着V或W的增大而增大,导致整个落点分布更为分散,而最终的错误率随着W的增大而降低,因为用户多倾向于点击目标的中心点,使得这种降低错误率的速度比W导致的落点分散趋势更快,从而出现了图3 所示的错误率变化曲线.

4.2 实验2:辅助目标选择技术

在本实验中,我们实现了一种基于交互计算模型的辅助目标选择技术ICOMPointer.使用实验1 中拟合得到的数据模型,当一次选择事件被触发时,计算机根据意图理解模块推测出用户的意图目标并做出响应.为了避免用户有意点击空白区域时模型仍会返回目标,忽略了落在目标二维正态分布3Σ范围之外的点击.进一步地,我们通过一个真实的游戏任务对比分析了ICOMPointer 与基本选择技术及两种现有的运动目标选择增强技术Bubble[46]、Comet[47]在表现上的差异.其中,Bubble 能够根据周围的目标位置动态改变光标选择区域,Comet 则是根据目标的运动速度和宽度给目标添加尾部,从而扩大其可选区域.

4.2.1 参与者及实验设备

我们共招募了16 名人员参与实验,其中有6 名女性,并且有12 名人员参与了实验1.他们的平均年龄为26岁.惯用手均为右手,且日常都有使用计算机的需要.实验所用的设备与实验1 相同,但是游戏程序基于Unity3D开发.

4.2.2 实验任务与设计

实验的程序界面如图4 所示,当用户开始实验后,屏幕上会在随机的位置出现15 个小球,它们以相同的预设大小和速度朝随机的方向运动,当碰到边界后无能量损失地反弹.其中,红色的球为目标球,用户需要尽可能快速并准确地选中目标.与实验1 不同,只有选中目标才有新的目标出现.

实验共有3 个独立变量.

(1)选择技术:Basic(基本选择技术)、Bubble、Comet、ICOMPointer(动态交互计算模型选择技术).

(2)目标大小(W):24 pixels、48 pixels、96 pixels、144 pixels.

(3)目标速度(V):96 pixels/sec、192 pixels/sec、288 pixels/sec、384 pixels/sec.

每位实验者需要在每种条件下完成10 次操作,因此总次数为4×4×4×10×16=10240 次.在实验进行前会先让实验者练习,并且在实验过程中也允许实验者暂停休息.

我们记录了所有W×V条件下的完成时间和错误率.完成时间是指从每一次操作开始到实验者选中目标之间的时间.错误率则是用户按下鼠标按钮没有选中目标的次数除以总点击次数.当用户完成实验后,需要填写一份总分为7 分的李克特量表,根据实际体验对每种选择技术的喜好程度打分,并填写主观评价.

4.2.3 实验结果

我们使用重复测量方差分析方法对实验数据进行分析.结果表明,选择技术对用户的平均完成时间有显著性影响(F3,45=30.688,p＜0.001).使用Bonferroni 校准成对比较不同选择技术在平均完成时间上的表现,结果表明,除了ICOMPointer 与Comet 无显著性差异(p=1.0)外,其余技术对之间均存在显著性差异(p＜0.05).在这4 种选择技术中,ICOMPointer 的平均完成时间最短(1 099ms),其次是Comet(1 138ms)、Bubble(1 324ms)和Basic(2 657ms).图5 所示为两种选择技术在不同目标大小与不同目标运动速度下的平均完成时间对比.

分析也表明,选择技术对用户的选择错误率有显著性影响(F3,45=75.306,p<0.001).使用Bonferroni 校准成对比较不同选择技术在错误率上的表现,结果表明,4 种技术对之间均存在显著性差异(p<0.05).ICOMPointer 的错误率最低(14%),接着依次是Comet(20.9%)、Bubble(32.7%)以及Basic(54.7%).图6 所示为两种选择技术在不同目标大小与不同目标运动速度下的错误率对比.

我们还分析了在每种选择技术下目标大小(W)和目标运动速度(V)对完成时间和错误率的影响,p值结果见表2.可以看出,W和V对Basic、Bubble 以及Comet 技术的完成时间或错误率具有显著性影响,而对ICOMPointer的完成时间和错误率均没有显著性影响.因此,我们的技术在面对不同大小和运动速度的目标时都能够表现出很好的稳定性.

Table 2 P value of the impact of W and V on four selection techniques表2 W 和V 对4 种选择技术影响的p 值

测试者填写的李克特量表结果表明,测试者对ICOMPointer 的喜好程度(M=5.82,SD=0.98)高于Comet(M=5.72,SD=1.34)、Bubble(M=5.36,SD=1.43)以及Basic(M=2.73,SD=1.55).在测试者的主观评价中也提到:“使用ICOMPointer 技术选择看起来与基本选择技术很像,但是选择目标更快.”[S1]“Bubble 虽然很快,但在目标较大或者非常密集时很难选中.”[S11]

4.2.4 讨 论

从实验结果可以看出,测试者使用ICOMPointer 能够用更短的时间选中目标,并且错误率也更低.速度和大小的整体影响结果也符合我们的预期.目标越大,用户的完成时间就越短,错误率也就越低.目标速度越大,用户的完成时间就越长,错误率也越高.

我们还发现,ICOMPointer 处于不同目标大小和运动速度时具有较强的鲁棒性,能够更好地适应目标的变化.即使目标大小和速度发生变化,依然可以辅助用户更快、更准地选中目标.在实际应用中避免了任务差异对用户选择稳定性的影响.而用户的反馈结果也表明ICOMPointer 更受欢迎.

5 结 语

本文提出了一个面向动态交互任务的定量化可计算的交互模型ICOMDT,该模型能够解释用户与动态任务的交互行为并实现用户意图预测.我们将该模型应用在运动目标获取任务中,提出一套可计算的模型方法,实验结果表明该模型能够很好地拟合用户数据.进一步地,我们将模型用于用户点击错误率预测和辅助运动目标选择中,发现错误率的预测值与实际值非常接近,并且能够有效地提高运动目标的选择效率.

目前对用户与动态交互任务的研究,大多停留在用户行为表现层,没有一套完整的、可计算的用户行为内部模型框架.ICOMDT模型的提出填补了这一空白,对计算机理解用户意图、提高用户与动态任务的交互效率有着重要意义.基于ICOMDT模型,开发者在设计动态交互任务时,可以通过模拟用户操作进行设计优化,如在游戏设计中通过预测用户的错误率调整任务参数;而对于复杂的操作控制系统,也可以通过用户意图理解提高交互效率,如在航班管理系统中使用辅助目标选择技术帮助操作员更容易选中要查看的航班信息.

但在本文的研究中,仍存在一些不足.如没有对用户具体的感知过程、认知过程与运动过程建立模型;没有考虑多通道信息输入的动态交互任务对用户交互过程产生的影响.在未来的研究工作中,我们希望进一步探索可计算的用户感知、认知与运动模型,并能够将我们的ICOMDT模型框架应用在具体的交互系统中.