深海爬游机器人多腿位姿对巡游稳定性的影响

张康，王磊，冷文军，陈虹

武汉第二船舶设计研究所，湖北武汉430205

0 引 言

深海爬游机器人（Crawling-Swimming Vehicle，CSV）是一种既可在深海巡游，又可在海底爬行的新型无缆无人潜航器，兼具自主式无人潜航器（Autonomous Underwater Vehicle，AUV）高效、大范围机动的能力，以及遥控式无人潜航器（Remotely Operated Vehicle，ROV）精确定位的能力，其主要结构如图1 所示［1-2］。CSV 艉部有2 个导管桨，可控制巡游速度和方向，携带有一次/二次大功率电源，通过可弃压载可快速下沉和上浮。深海爬游机器人总重约2 000 kg，有效负载100 kg，极限下潜深度1 000 m，巡航速度1.0 m/s，最大巡游速度1.5 m/s，最大爬行速度0.1 m/s，最大工作坡度15°，能在1.5 m/s 的洋流下正常工作［1］。CSV 主要由主体、螺旋桨以及外附的6 条腿组成，在水中巡游时，多腿的不同位姿会改变周围流场以及自身重心的分布，影响其整体的受力及运动特性。因此，掌握CSV不同位姿下的水动力性能及稳定性规律，对其控制及安全运行具有重要意义。

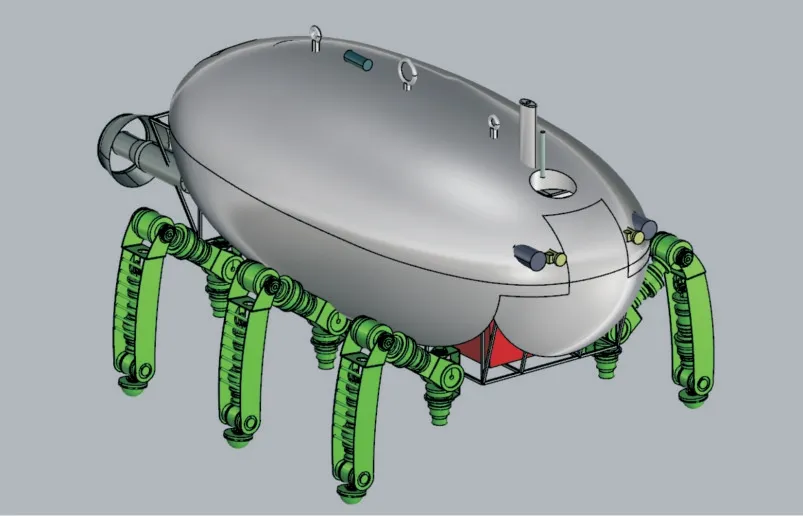
图1 深海爬游机器人示意图Fig.1 Schematic diagram of deep-sea CSV

以往的研究多针对流线型回转体潜航器，分析潜航器的受力多采用潜艇操纵性平面运动方程，而缺少对前后近似对称、上下不对称潜航器操纵性运动方程的研究，也缺少对外附多腿潜航器巡游运动稳定性的研究。Jun 等［3-5］对水下仿蟹机器人（CR200）进行了研究，但未考虑水下多足机器人在巡游过程中的水动力。Jun 等［3］提出的仿蟹机器人腿部阻力和升力近似模型、Kang 等［4］研究的仿蟹机器人腿部主动控制和反馈控制水动力模型，以及Park 等［5］基于CR200 模型试验得到的水动力和力矩，考虑的都是水下多足机器人在爬行过程中腿部的受力。在潜航器稳定性研究方面，黄明龙［6］研究了尾翼、外形对回转型AUV 运动稳定性的影响，孙梦瑶等［7］研究了测量型深水AUV垂直面的运动稳定性，所研究的对象都是常规外形的潜航器，同时都借鉴了潜艇的稳定性判据。在潜航器操纵性水动力研究方面，张晓频［8］计算的多功能回转体潜航器、张赫［9］研究的长航程潜航器，以及徐树峰［10］研究的某新型水下机器人也都是常规外形潜航器。综上而言，目前操纵性水动力和稳定性的研究对象普遍为流线型、结构较为集中的潜航器，鲜有对外附多腿复杂结构潜航器的研究。CSV 结构与传统潜航器结构相差很大，不能直接采用潜艇的操纵性平面运动方程建立稳定性判据，同时，因多腿结构复杂，在非定常计算中网格容易出现畸变。

本文将首先建立CSV 的操纵性垂直面运动方程和稳定性判据，通过计算椭球体模型验证算法和混合网格的有效性，采用统一的算法和近似一致的网格划分，计算CSV 不同位姿的操纵性水动力并与试验值进行比较，然后根据判据分析CSV不同位姿稳定性的优劣。

1 操纵性运动方程与稳定性判据

1.1 操纵性垂直面运动方程

将CSV 的主体建模为近似椭球体，6 条腿建模为外附的细长圆柱。CSV 的结构为左右对称、前后近似对称、上下不对称，与常规潜航器区别较大。针对该特点，建立新的操纵性平面运动方程。

采用与潜艇研究设定的坐标系相同的固定坐标系E-ξηζ和运动坐标系G-xyz［11］，如图2 所示（图中，X为纵向力，Y为横向力，Z为垂向力，K为横倾力矩，N为偏航力矩，M为俯仰力矩），将CSV 在垂直面作弱机动时的操纵运动方程简化为

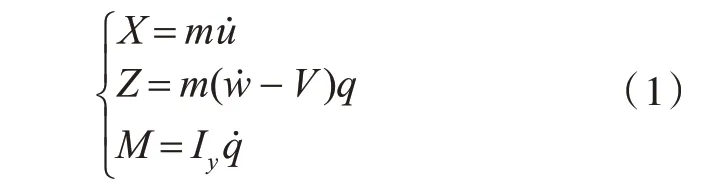
式中：m为CSV 质量；V为CSV 定常运动的速度；u˙为纵向加速度；w˙为垂向加速度；q为俯仰角速度；q˙为俯仰角加速度；Iy为CSV 对Gy轴的转动惯量。

图2 固定坐标系和运动坐标系Fig.2 Fixed coordinate system and moving coordinate system

采用模型进行试验时，考虑到惯性力和粘性力的思路，将CSV 受到的流体动力线性化为

式中：X0为CSV 直线航行时的阻力；Δu为纵向速度变化量；w为垂向速度；X0+XuΔu为CSV 定常运动时的阻力；Z0，M0分别为零升力和零升力矩；Xu，Xu˙分别为纵向速度和加速度诱导的纵向力系数；Zw，Zw˙，Mw，Mw˙，Zq，Zq˙，Mq，Mq˙为水动力系数，其含义相似。

与潜艇不同，由于CSV 左右对称、前后近似对称、上下不对称，所以式（2）中Zq˙=Mw˙=M0=0 ，Z0≠0。

由于CSV 作弱机动，因而u˙=0。假设螺旋桨合推力轴线与Gx 轴重合，计及非流体动力，将式（2）简化后代入式（1），得到CSV 垂直面操纵运动线性方程式为

式中：P为剩余静载荷；Mp为剩余静载力矩；Mθθ为扶正力矩；θ为纵倾角。

将式（3）与潜艇的垂直面操纵运动线性方程［11］进行对比可以发现，潜艇需要考虑舵产生的流体动力以及螺旋桨产生的纵倾力矩。由于潜艇前后不对称，故潜艇的操纵运动线性方程式中保留有零升力矩M0和Zq˙，Mw˙，只有认为潜艇对称于自身中横剖面时，操纵运动方程式中的Zq˙=Mw˙=0。

1.2 稳定性判据

CSV 在垂直面受到瞬时弱干扰时，仅攻角发生了变化，引起的流体动力也产生了相应的变化。若攻角细微变化引起的流体动力促使攻角恢复原来状态，则CSV 静稳定，反之，则静不稳定。因攻角变化只涉及角位移问题，故只需分析变化的流体动力力矩M(w)的作用趋向，即分析水动力中心点与重心的纵向相对位置即可。其此时的情形与潜艇相同，因而采用与潜艇相同的静稳定性判据［11］，即

由式（3）消去θ，与潜艇类似，认为Z0已经在基准运动中被均衡［11］。将航速改变导致的差异计入剩余静载荷P和剩余静载力矩Mp，得到无因次化后攻角的响应线性方程式为

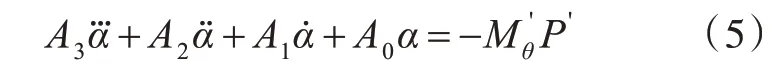
由式（5），得到扰动运动方程的特征方程式为

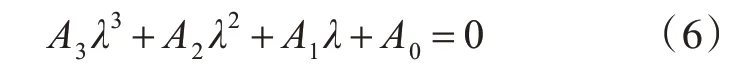
式中，λ为特征方程的特征根。

根据古尔维茨判别法，CSV 在垂直面内动稳定的充要条件为

当CSV 处于条件动稳定状态时，表示在低速区是稳定的，但高速后不一定动稳定。由稳定转变为不稳定的临界速度Vcr，根据式（8），当Kvd=1时，得

若CSV 无法满足绝对的动稳定，则设计航速应该低于临界速度，以保证具有一定的条件动稳定性。

将CSV 的稳定性判据与潜艇的［11］进行对比可以发现，二者扰动运动的特征方程式（6）的系数不同，但最终的判据（式（8））却相同。这是因为由潜艇的扰动运动特征方程建立动稳定性判据时，潜艇被假定为前后对称，这点与CSV的结构特征相同，即Zq˙=Mw˙=0，此时，潜艇扰动运动的特征方程式与式（6）相同，因而二者最终的稳定性判据相同。

1.3 操纵性水动力系数

在对CSV 的纯升沉运动和纯俯仰运动进行仿真时，设定CSV 的运动规律如式（10）和式（11）所示，计算得到CSV 的垂向力系数Z'和俯仰力矩系数M'，然后按照式（12）和式（13）处理数据，得到相关操纵性水动力系数并代入判据式（8），即可判定CSV 垂直面的稳定性。

式中：ζ为CSV 的垂向位移：a为CSV 纯升沉运动振幅；ω为CSV 升沉运动的圆频率；˙为CSV 的纵倾角速度；θ0为CSV 纯俯仰运动振幅；，其 中 L 为 CSV 主 体 长 ；；；；；；。

2 计算模型与边界条件

研究3 种典型的CSV 位姿：纵向展开位姿（CSV-1）、横向展开位姿（CSV-2）和落底位姿（CSV-3），如图3 所示。模型关于中纵剖面对称，主体长L=2 700 mm，宽B=1 260 mm，高D=916 mm；6条腿相同，第1节建模成细长圆柱体，长L1=424 mm，直径85 mm，第2 节建模成细长椭圆柱体，长L2=600 mm，横截面椭圆长、短轴分别为150 和103 mm；中纵剖面同侧前腿（Leg1）与中腿（Leg2）之间距离d1=727 mm，中腿（Leg2）与后腿（Leg3）之间距离d2=783 mm，两侧2 条腿之间距离为864 mm。计算域范围：-5L≤X≤2L，-2L≤Y≤2L，-2L≤Z≤2L。综合结构化网格数量少和非结构化网格适应性强的优点，对计算域划分混合型网格，如图4（a）所示。内域是半径为L 的球体，划分非结构化网格；整体域减去内域即为外域，划分结构化网格。计算时，CSV 与内域网格保持相同的规律一起运动，只在外域底层发生网格变形，这样可以有效避免非定常运动时的网格畸变问题。在内域与外域的交界面处设置接触，混合网格有效性验证如表1 所示。综合考虑计算精度与时间等因素，完成网格无关性分析（表2）后，划分整体网格数量约为162 万。

表1 为椭球体直航阻力计算值与试验值［12］的对比，表中计算值表示对椭球体划分混合网格的计算结果。从表中可以看出，混合网格模型的计算精度很高，可以用来计算CSV 的操纵性运动。

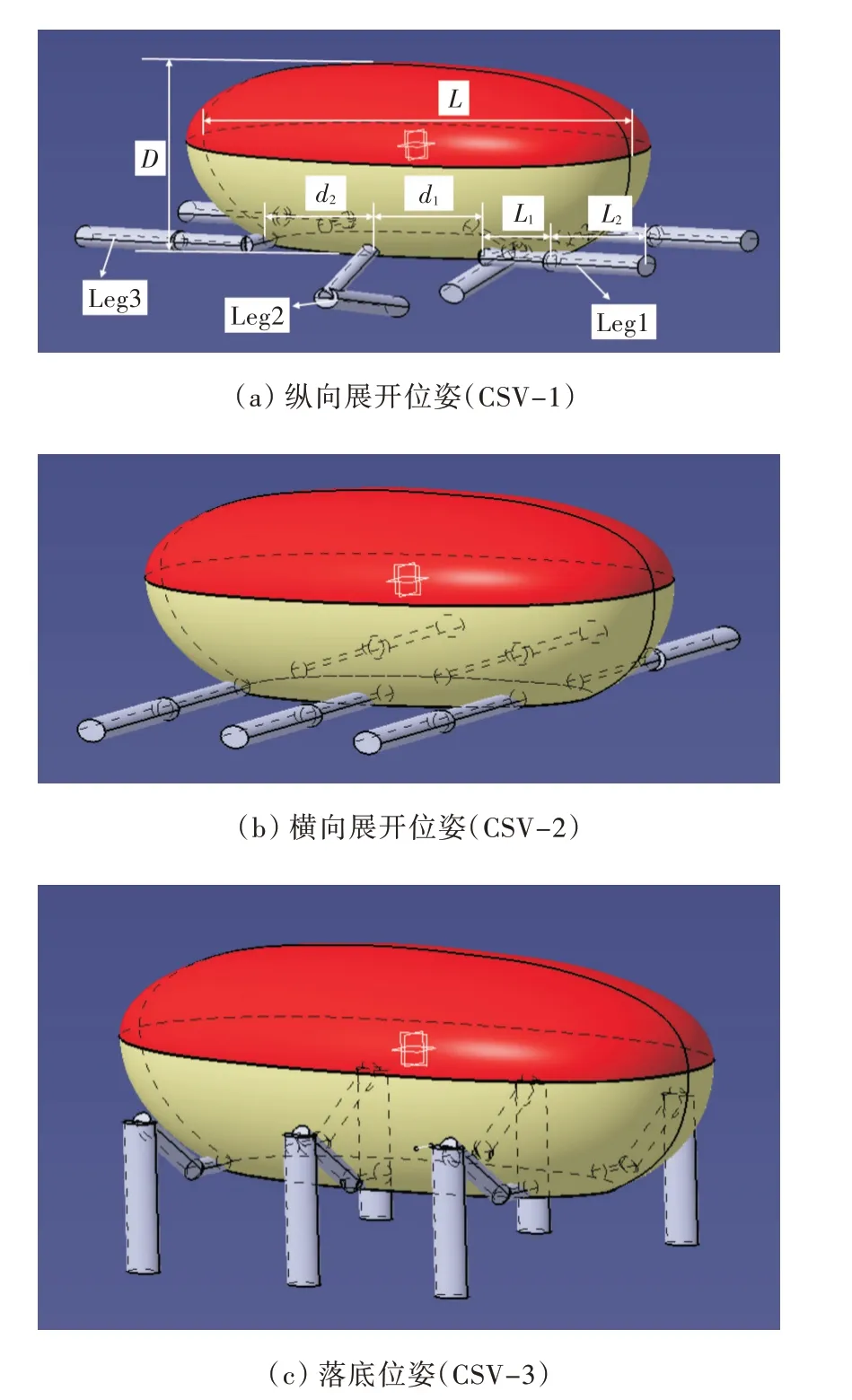
图3 CSV 不同结构布置Fig.3 Different arrangements of CSVs structure

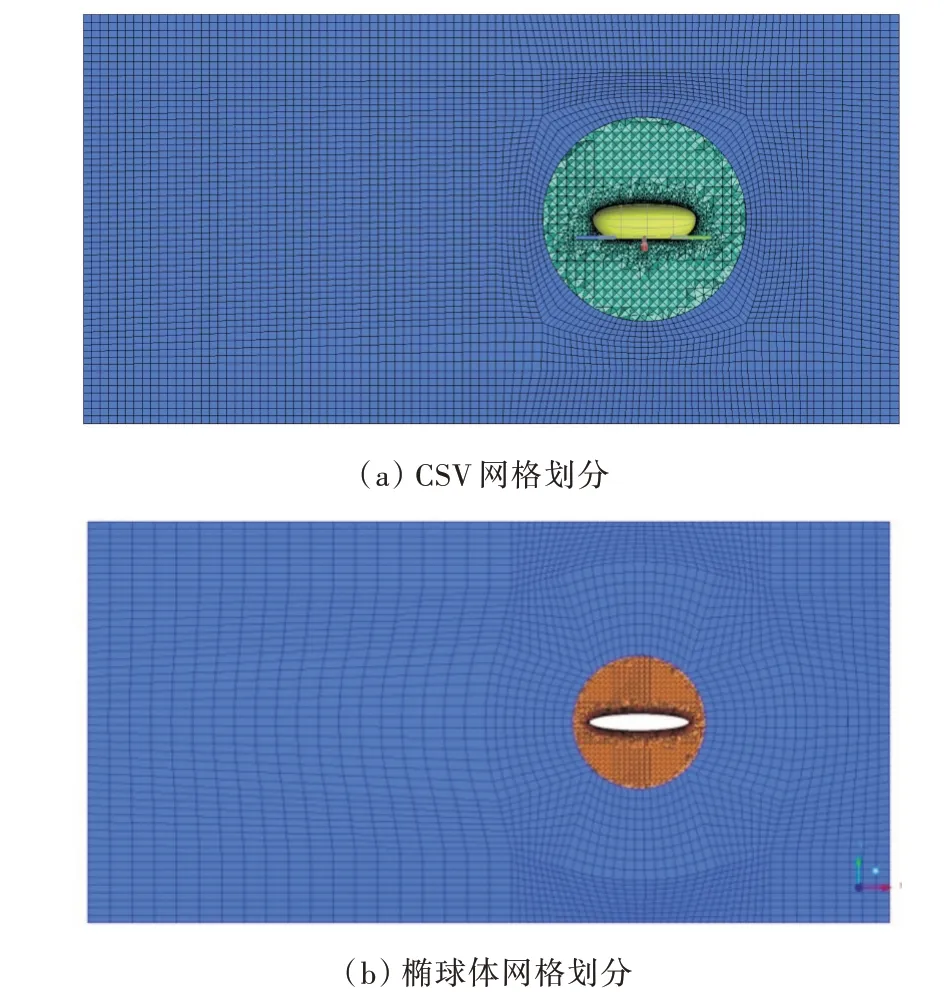
图4 计算模型及计算域网格Fig.4 Computational model and domain meshes

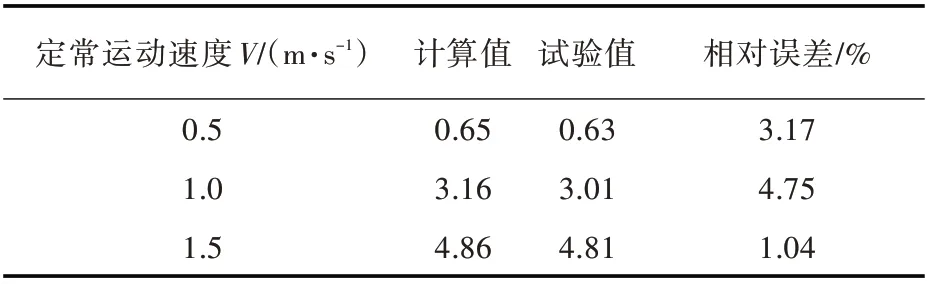
表1 椭球体直航阻力的计算值与试验值Table 1 Computational and experimental resistance values of ellipsoid

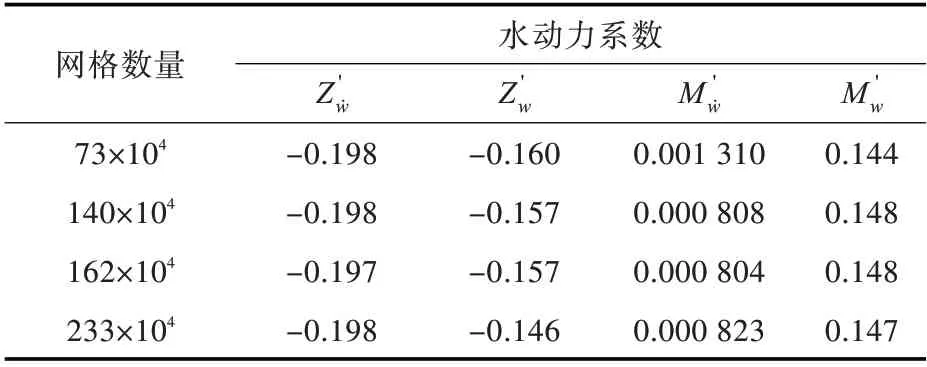
表2 CSV-1 不同网格数量下纯升沉运动的水动力系数Table 2 Pure heaving motion hydrodynamic coefficients of CSV-1 with different meshes

表2 为振荡频率f=0.5 Hz 时CSV-1 划分不同数量网格的纯升沉运动计算结果，从中可以看出，不同网格数量下求解的水动力系数相差较小，本文选用的162 万网格收敛性良好。

计算之前，先根据CSV 的运动规律编译用户自定义函数（User Defined Function，UDF）。在利用Fluent 软件调用UDF 程序进行计算时，设定内域网格与CSV 保持相同的频率和相位运动。采用弹性光顺法更新动网格，当内域的运动振幅小于外域底层网格尺寸时能够有效避免网格畸变。

本文选择分离隐式求解器，采用有限体积法离散计算域和控制方程，选择标准k-ε湍流模型封闭控制方程，采用PISO 算法求解速度与压力耦合场。计算域采用速度入口边界条件，雷诺数Re=2.69×106，出口边界采用自由出流，边界采用固壁条件。

对椭球体进行计算验证时，按同样的方法划分混合网格，如图4（b）所示。整体网格数量为32万，计算方法和边界条件等的设置与CSV 相同。

3 计算结果与分析

3.1 数值验证

通过对椭球体的纯升沉运动和纯俯仰运动进行仿真，验证数值算法的有效性。设定椭球体纯升沉运动来流速度为0.8 m/s，振幅a=0.04 m，振荡频率依次为f=0.4，0.5，0.6 Hz，计算5 个周期运动，每个周期设定400步。纯俯仰运动振幅θ0=0.1rad，来流速度、频率、周期等的设定与纯升沉运动相同。

图5 给出了椭球体纯俯仰运动中垂向力系数随时间的周期变化曲线（图中，Z' 为垂向力系数）。由图中可以看出，垂向力系数呈稳定周期性变化，且峰值随振荡频率的增大而依次递增，与工程经验相符。

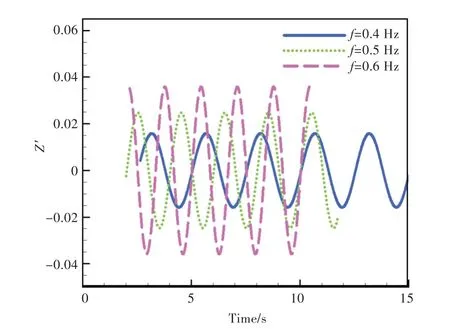
图5 椭球体纯俯仰运动垂向力系数随时间的周期变化曲线Fig.5 Periodic variation curves of ellipsoid pure pitching motion vertical force coefficients with time

表3 椭球体纯升沉运动水动力系数的计算值与图谱值Table 3 Computation and map values of ellipsoid pure heaving motion hydrodynamic coefficients

3.2 计算结果

对CSV 的纯升沉运动和纯俯仰运动展开研究。设定运动振幅与椭球体相同，来流速度为1.0 m/s，振荡频率f = 0.3，0.4，0.5，0.6 Hz，计算5 个周期的运动，每个周期400 步。

图6、表4 和表5 给出了3 种位姿的CSV 纯升沉运动与纯俯仰运动计算结果。图6 为CSV-1 纯升沉运动垂向力系数随时间的变化曲线，从图中可以看出，垂向力系数呈稳定周期性变化，且随着频率的增加，垂向力系数峰值递增，这与工程经验相符。

图6 CSV-1 纯升沉运动垂向力系数随时间的周期变化曲线Fig.6 Periodic variation curves of CSV-1 pure heaving motion vertical force coefficients with time

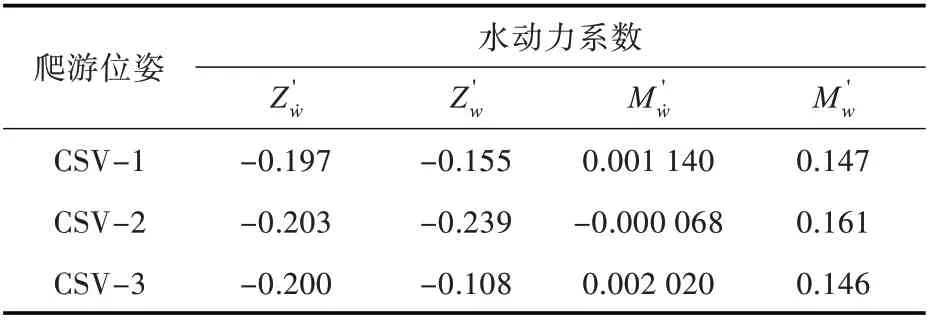
表4 CSV 不同位姿纯升沉运动水动力系数Table 4 Pure heaving motion hydrodynamic coefficients of CSV with different poses

表5 CSV 不同位姿纯俯仰运动水动力系数Table 5 Pure pitching motion hydrodynamic coefficients of CSV with different poses

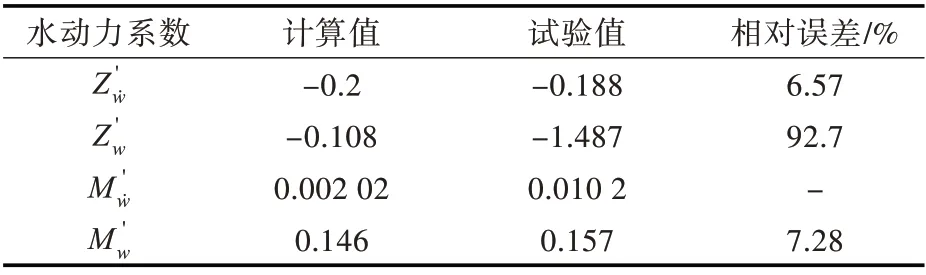
表6 CSV-3 纯升沉运动水动力系数的计算值与试验值Table 6 Computation and experiment results of CSV-3 pure heaving motion hydrodynamic coefficients

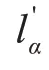
表7 CSV 不同位姿的运动稳定性判据Table 7 Motion stability criteria of CSV with different poses

图7 不同位姿下垂直面静稳定性系数的分量Fig.7 Components of vertical plane static stability coefficients at different poses

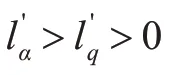
图8 不同位姿下垂直面动稳定性系数的分量Fig.8 Components of vertical plane dynamic stability coefficient at different poses

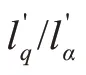
图9 不同位姿下 的分量Fig.9 Components of at different poses

图10 不同位姿下 的分量Fig.10 Components of at different poses

综上所述，3 种位姿的CSV 在垂直面均处于静不稳定、条件动稳定状态，与潜艇的稳定性不同，CSV 设计的最大航速在1.5 m/s 左右，没有达到临界速度Vcr，能够达到直线自动稳定，满足了深度控制和安全航行的要求。

4 结 论

本文针对CSV 垂直面稳定性进行了研究，并将CSV 建模为主体外附多个相同的附体。针对CSV 左右对称、前后近似对称、上下不对称的结构，建立了新的操纵性垂直面运动方程，进而建立了CSV 的运动稳定性判据，并研究了CSV 的纯升沉运动和纯俯仰运动。通过对数值验证及计算结果的分析，得到以下几点结论：

1）3 种位姿的CSV 在垂直面都是静不稳定与条件动稳定状态，与潜艇的稳定性有所差异，临界速度在2 m/s 左右，在设计航速（最大1.5 m/s）内能满足直线稳定的要求。

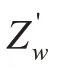
本文的计算对象为非流线型复杂结构，因周围流场比较复杂，故只研究了CSV 的垂直面稳定性，下一步拟对CSV 的水平面稳定性展开数值和试验研究。