三维片上网络高维超立方裂变拓扑结构研究*
2019-10-24梁华林张大坤
梁华林,张大坤
天津工业大学 计算机科学与技术学院,天津300387
+通讯作者E-mail:zhangdakun2018@163.com
1 引言
现代芯片需要将大量的功能和存储核心(也称IP 核,intellectual property block),如音频和视频处理器、存储器、I/O外设和硬件加速器等,集成到一个芯片上进行交换数据以实现多媒体和网络服务。早期的IP 核通讯由于缺少合理的设计限制了芯片的性能。在这种情况下片上系统(system-on-chip,SoC)和二维片上网络(two-dimensional network-on-chip,2D NoC)应运而生。然而,随着2D NoC 的发展,其在规模、性能和布线方面都出现了瓶颈[1]。三维片上网络(three dimensional network-on-chip,3D NoC)在这种情况下被提出,近年来国内外学者对其进行了广泛的研究[2-5]。
在3D NoC研究中,拓扑结构是关键问题之一[6];关于片上网络拓扑结构的研究主要有两方向:其一,对已有三维片上网络拓扑结构的改进与优化;其二,研究新型网络拓扑结构。目前,关于经典三维片上网络拓扑结构路由算法改进的研究较多,如Ashokkumar等人提出了通过编码解码方法对3D Mesh 的路由算法进行优化[7];上海交通大学Yao 等人设计了路由寻路单元对3D Torus寻路进行了优化[8];而对于新型拓扑结构的研究报道较少,与经典拓扑结构相比,新型拓扑结构更能适应特定情况下的特殊要求,而且一部分针对经典拓扑结构的路由算法也可以移植到新型拓扑结构中,如北德克萨斯大学Mohanty等人提出了改进3D NoC 蝶形胖树网络拓扑结构[9];Chen 等人提出的基于De Bruijn图的新型3D NoC拓扑结构[10];湖南大学贺旭等人提出了三维超立方体片上网络拓扑结构[11];西安电子科技大学刘有耀等人根据Torus拓扑结构提出了新型拓扑结构及其路由算法等[12]。其中,超立方体拓扑结构具有对称性好、网络直径短、可扩展性高等优点。然而,随着超立方体维度的增加,其节点间连线数量急剧增加,因而出现通讯瓶颈。在国家自然科学基金(课题号:61272006)研究过程中发现,将三维模型裂变思想用到超立方体拓扑结构中能够有效地克服超立方体拓扑结构的缺点。本文提出了三维片上网络五维超立方裂变拓扑结构,该拓扑结构对超立方体结构使用“裂变”方法来增加节点,代替以往网络规模扩大时从边缘增加节点的“加法”操作,既保留了超立方体拓扑结构的优点,又解决了高维超立方体拓扑结构的通讯瓶颈问题。
2 超立方体裂变拓扑结构的提出与分析
2.1 三维模型裂变思想
在国家自然科学基金课题“基于柏拉图立体多级裂变模型的三维片上网络拓扑结构”研究中,提出了柏拉图立体多级裂变模型的思想:将三维模型的每个节点沿相关联的边移动一段距离后生成新的节点,三维模型的规模得到扩大,使三维片上网络规模的扩大由一般的增加行或列的“加法”变成了从内部生成新节点的“裂变”。本文将该模型裂变思想应用于超立方体拓扑结构中。
2.2 超立方体拓扑结构简介
三维片上网络超立方拓扑结构具有对称性好、可扩展性高以及网络直径短等优点[11]。三维超立方体节点数较少,应用受到限制,而四维、五维等高维超立方体保持了良好的对称性,节点数增多,应用范围扩大,但是节点度数也随之增加。在五维超立方体结构中,包含32 个节点,80 条边,每个节点的节点度数为5,如图1所示。
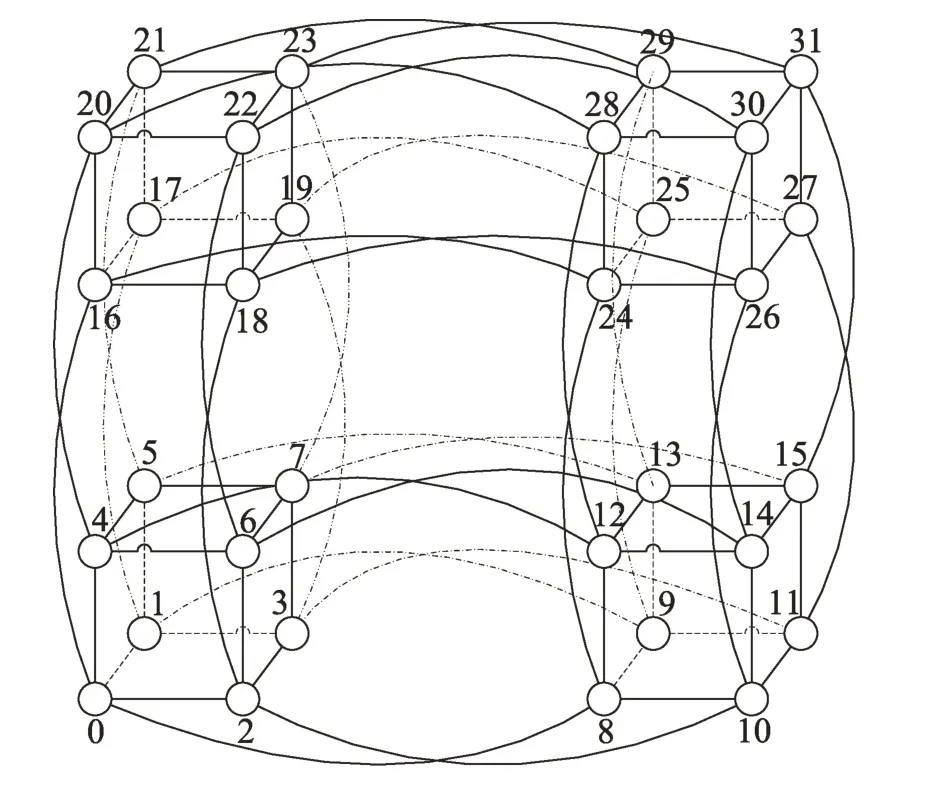
Fig.1 Five-dimensional hypercube topology图1 五维超立方体拓扑结构
2.3 超立方裂变拓扑结构的定义及生成
本文将三维模型裂变思想用于高维超立方体中,以五维超立方体为例,提出了五维超立方裂变拓扑结构,该拓扑结构既保留了超立方体拓扑结构原有的优点,又解决了高维超立方体结构的通讯瓶颈问题。
2.3.1 超立方裂变拓扑结构的定义
超立方体维度增加时,节点间连线数量急剧增加,路由算法复杂度也随之增加。本文将三维模型裂变思想用到超立方体拓扑结构中。超立方裂变拓扑结构是由超立方体拓扑结构通过两步生成的,第一步是“裂变”,第二步是“互连”。
2.3.2 超立方裂变拓扑结构的生成
三维片上网络中的节点一般都包含一个路由器和固定数量的IP 核,IP 核一般是处理器中的功能部件,核之间通过路由器进行路由通讯,以节点0 的裂变为例说明超立方裂变拓扑结构的生成过程。将节点0裂变为5个子节点,分别编号00、01、02、03和04,然后顺时针连接这5 个子节点,从而形成一个闭环,再将原节点0 删除,这样就形成了一个小的裂变簇。将剩下的31 个节点做同样的处理,就形成了五维超立方的裂变拓扑结构。具体的裂变过程如图2所示,其中的圆圈代表网络节点。
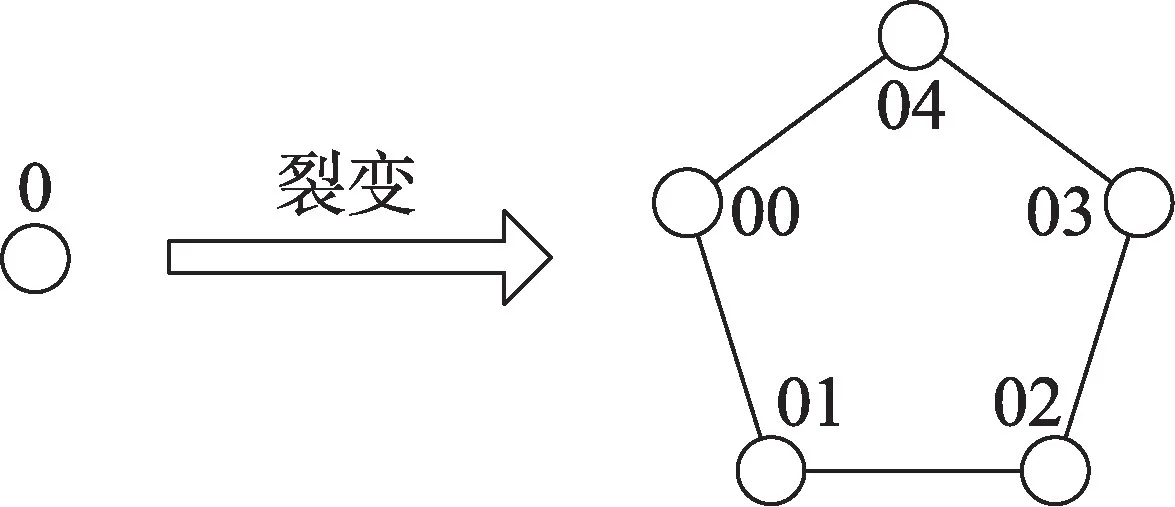
Fig.2 Fission process of node 0图2 节点0的裂变过程
裂变簇之间的连接过程如下,以0号节点对应的裂变簇0为例,将裂变簇0中的子节点与其关联的其余5个裂变簇中对应的子节点用物理链路进行连接,例如:节点00 与节点10、20、40、80 和160 进行相连。于是便完成了裂变簇0 与其相关联裂变簇之间的连接。裂变簇0 最终的连接结果如图3 所示。对其余裂变簇中的子节点都进行如上的操作,最后就形成了五维超立方裂变拓扑结构。
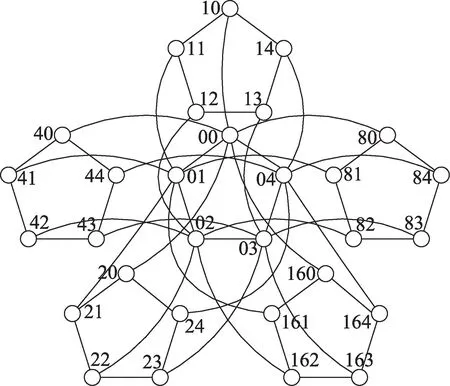
Fig.3 Connection relationship between node 0 and its associated fission nodes图3 节点0及其关联裂变节点的连接关系
2.4 超立方裂变拓扑结构与经典拓扑结构对比
在相同节点数情况下,从网络对分带宽和最大节点度两个方面,将高维超立方裂变拓扑结构与3D Mesh 的结构特征进行比较。首先,高维超立方裂变拓扑结构的对分带宽明显高于3D Mesh 结构的对分带宽。
以五维超立方裂变结构为例:在160个节点规模情况下,五维超立方裂变拓扑结构的对分带宽为80,而3D Mesh 结构的对分带宽为40,五维超立方裂变拓扑结构的对分带宽恰好为3D Mesh 对分带宽的2倍;其次,对最大节点度进行对比,3D Mesh结构的最大节点度为4,而高维超立方裂变拓扑结构的节点度为N+2。具体性能指标对比如表1所示。

Table 1 Comparison of performance between hypercube fission topology and classical one表1 超立方裂变结构与经典结构性能指标对比
3 超立方裂变拓扑结构编码和路由设计
3.1 节点编码
考虑到存储的占用,对于超立方裂变拓扑结构的编码采用格雷码编码机制。高维超立方裂变拓扑结构中节点的编码分为两部分:簇内编码和簇外编码。其中簇外编码所占位数与簇个数的关系为:

其中,NoutCode为簇外编码所占位数,NoutNode为簇个数。簇内编码所占位数与裂变节点个数的关系为:

其中,NinCode为簇内编码所占位数,NinNode为裂变节点个数。下面以五维超立方裂变拓扑结构为例说明高维超立方裂变拓扑结构编码格式及路由算法。编码分为两步:首先,对五维超立方节点进行编码,每个超立方节点需要5 位编码长度;其次,对裂变之后的子节点进行编码,由于一个裂变簇包含5 个子节点,因此每个子节点需要3位编码长度。之后将两步编码进行组合,将超立方节点编码向左移3位再加上裂变簇的子节点3位编码,组合之后形成的8位编码就是五维超立方裂变拓扑结构中一个节点的编码,其编码方式如表2 所示。采用这种编码方式能够降低路由协议的复杂度,从而达到提高网络性能,降低网络延时的目的。
3.2 路由器结构设计
在五维超立方裂变拓扑结构中,每个网络节点中的路由器有7 个与之相邻网络节点连接的端口和若干个本地端口,本仿真实验设计中每个节点搭载4个IP 核,故需要4 个本地端口,本地端口的一端与路由器相连,另一端与本地IP 核相连。每个端口包括输入通道和输出通道,每个通道可以从相连接的路由器或者IP核接收数据包或者发送数据包。其中每个物理通道又被划分为多个虚通道,一般被划分为2个、4 个或8 个,本仿真实验选取4 个虚通道,以便有效地避免死锁。路由器中包括路由逻辑、交换开关和虚通道仲裁单元等,通过路由算法把网络节点接收的数据包发送到正确的输出通道上,物理通道被各个虚通道采用轮转法使用。高维超立方裂变拓扑结构的最大节点度数随着维数的增加而增加,导致路由器结构也随节点度数的增加而变得更加复杂。
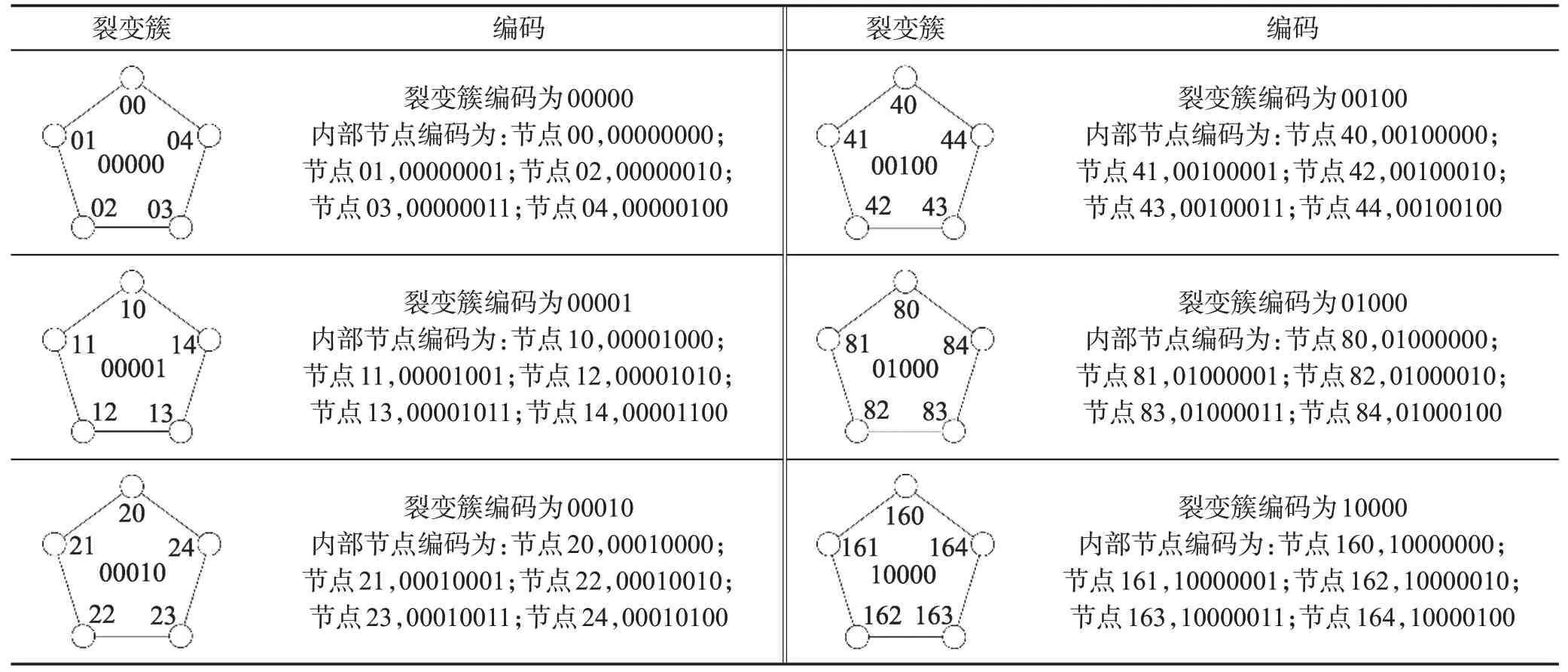
Table 2 Encoding of cluster 0 and its adjacent cluster表2 簇0及其相邻簇编码
3.3 路由算法设计
由于高维超立方裂变拓扑结构编码的前半部分是裂变簇的编号,后半部分是簇内节点的编号,因此路由算法的设计思路是先将数据包路由到目的裂变簇,等到数据包到达目的簇内再对簇内节点进行路由,最后由目的节点将数据包发送到指定IP 核。参数dest是目标地址,IPcoreBits是常数,表示的是IP核的编码位数。具体路由算法如下:
步骤1当超立方裂变拓扑结构中节点接收到数据包后,计算目的节点的路由地址destSwitch=dest>>IPcoreBits(取目的地址的路由位)。
步骤2判断目的节点的路由地址与当前路由地址是否相同(destSwitch和currSwitch是否相等),若相同则转向步骤7,否则继续执行。
步骤3分别计算目的路由器和当前路由器的簇内地址和簇外地址。
步骤4判断当前的路由和目的路由是否在同一簇内(flag=destCluster⊕currCluster,其中⊕为异或运算符),若在同一簇内(flag值为0),则继续执行,否则转向步骤6。
步骤5根据当前簇内地址的值(currClusterInner)和目的簇内地址的值(destClusterInner)进行物理信道的选取,将数据包发送到相应节点并将其节点地址更新为当前节点currSwitch地址值,转向步骤1。
步骤6将当前路由簇地址值与目标簇地址值从右起第一个不同的位置,记为m(m=destClusterInner⊕currClusterInner)。根据m的值设置物理信道,并将数据包发送到相应的节点上,更新当前节点currSwitch地址值,转向步骤1。
步骤7数据包到达目标节点,将数据包发送到对应的IP核。
4 超立方体裂变拓扑结构性能仿真
4.1 仿真实验设计
4.1.1 仿真平台与实验方案
本仿真实验以美国Rochester 大学Hossain 等人研发的gpNoCsim[13]仿真平台为基础,并对其进行了三维扩充,实现了五维超立方裂变拓扑结构和3D Mesh 拓扑结构及路由算法仿真。根据仿真实验结果,对两种拓扑结构的吞吐量、平均延时和平均跳数进行了对比分析。五维超立方裂变拓扑结构有160个网络节点,由于需要比较的两种结构的规模应该相同,因此将3D Mesh拓扑结构的网络规模大小设置为8×4×5。每个网络节点中路由器与4个IP核相连,故两种拓扑结构搭载的IP 核数都是640 个。在本仿真实验中,3D Mesh的路由算法采用XYZ路由算法[14-15],而五维超立方裂变拓扑结构则采用3.3 节中所设计的路由算法。仿真实验对于局部负载和均匀负载分别进行了仿真实验,均匀负载下,每个节点接收数据包的概率都相同;局部负载下,网络中70%的数据包都在单个节点簇内进行流动,30%的数据包则随机发送到簇外节点。
4.1.2 参数配置
GpNoCsim仿真器中主要的参数配置如下:虚拟通道数设置为4,每个缓存的微片数设置为4 flit,平均消息长度设置为160字节,微片长度设置为64位,IP核数设置为640,仿真实验每次运行20 000个时钟周期,其中预热期设置为10%,运行次数设置为20。
4.2 吞吐量对比分析
4.2.1 均匀负载模式下的吞吐量对比分析
通过仿真实验,在均匀负载模式下,得到了超立方裂变拓扑结构和3D Mesh 两种拓扑结构的网络吞吐量仿真实验数据。五维超立方裂变拓扑结构和3D Mesh 两种拓扑结构在均匀负载模式下吞吐量与注入率的关系曲线如图4所示。
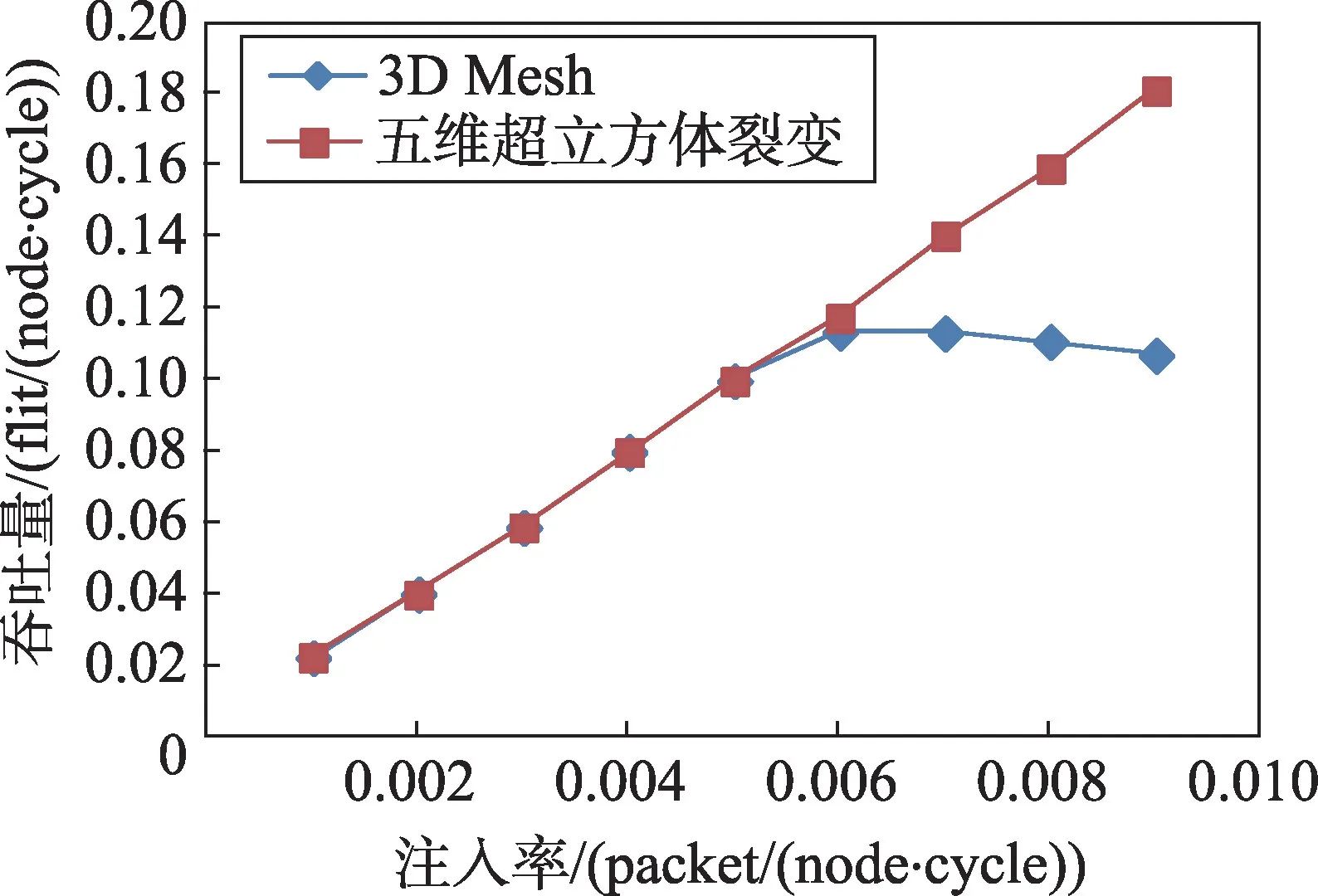
Fig.4 Contrast of throughput under uniform pattern图4 均匀负载模式下吞吐量的对比
由图4可见,当注入率小于0.006时,在相同注入率下,两种拓扑结构都没有出现拥塞,吞吐量基本相同;当注入率到达0.006时,3D Mesh拓扑结构首先出现了拥塞现象,说明其达到了饱和状态,此时吞吐量为0.11;当注入率达到0.016左右时,五维超立方裂变拓扑结构达到了饱和状态,此时其吞吐量为0.28,3D Mesh 拓扑结构的吞吐量为0.07;五维超立方裂变拓扑结构达到饱和时的吞吐量比相同状态下3D Mesh拓扑结构的吞吐量高300%。仿真实验结果表明,五维超立方裂变拓扑结构在均匀负载模式下,吞吐量明显高于3D Mesh拓扑结构的吞吐量。
4.2.2 局部负载模式下的吞吐量对比分析
在局部负载下,得到了五维超立方裂变拓扑结构和3D Mesh 两种拓扑结构的网络吞吐量与注入率关系的仿真实验数据,如图5所示。
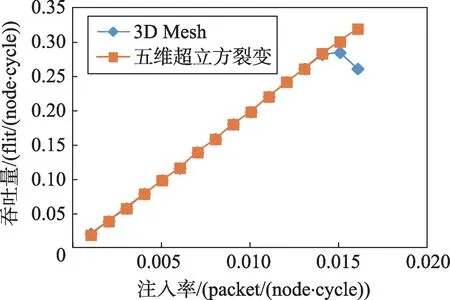
Fig.5 Contrast of throughput under localized pattern图5 局部负载模式下吞吐量的对比
由图5可知,当注入率小于0.013时,在同样的注入率下,两种拓扑结构的局部负载吞吐量相差很小;当注入率达到0.013时,3D Mesh网络达到饱和状态,此时吞吐量为0.28,继续增大注入率,则其吞吐量开始降低,这是由于发生了网络堵塞;而五维超立方裂变拓扑结构的吞吐量在仿真实验范围内未出现饱和状态。
4.3 平均延时对比分析
4.3.1 均匀负载模式下平均延时对比分析
由仿真实验数据得到了超立方裂变拓扑结构和3D Mesh 在均匀负载下平均延时与注入率之间的关系曲线,如图6所示。
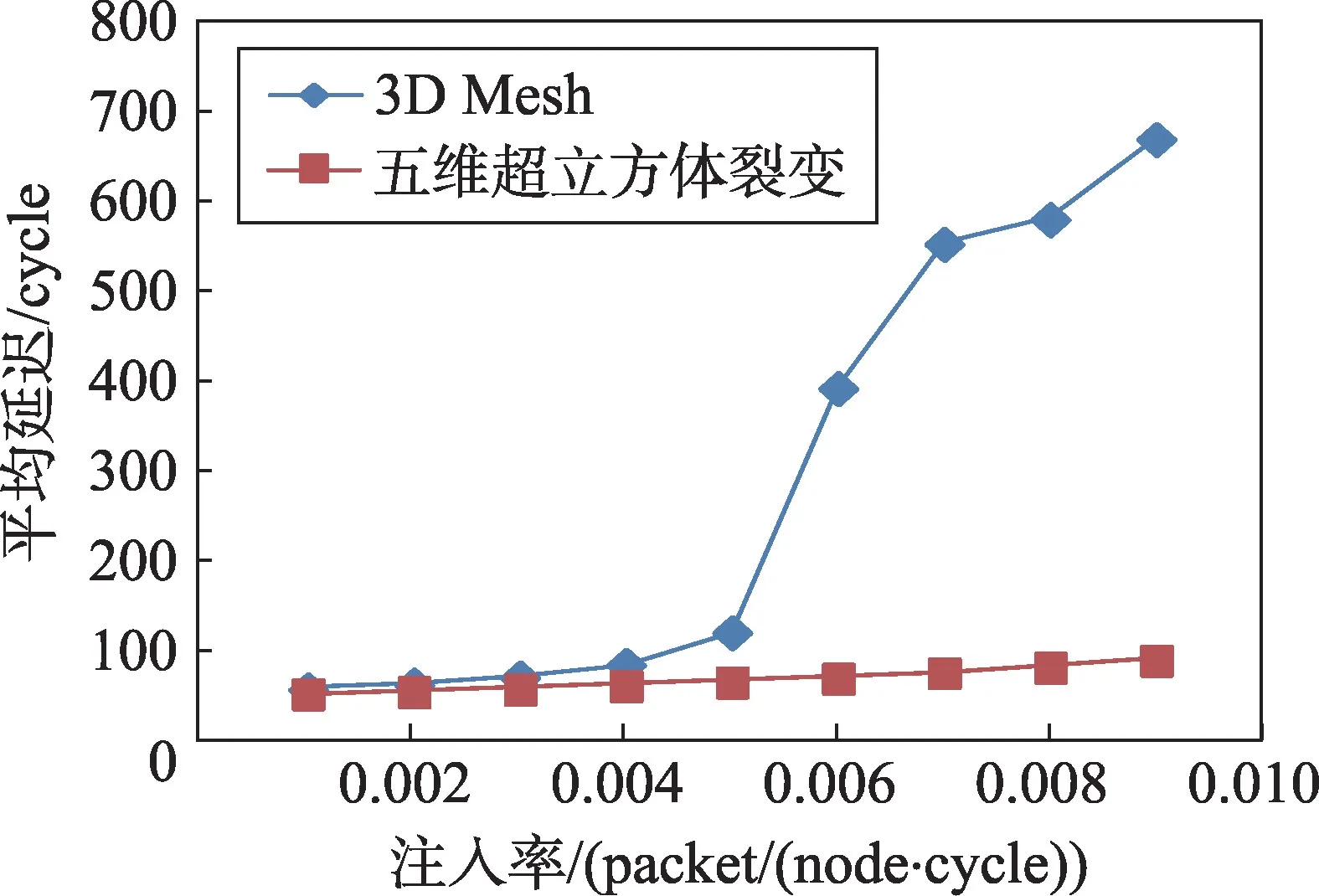
Fig.6 Contrast of average latency under uniform pattern图6 均匀负载下平均延时对比
由图6可知,在均匀负载下,当注入率大于0.005时,相对于五维超立方裂变拓扑结构,3D Mesh 拓扑结构的平均延时有一个阶梯式的增长,而随着注入率的增加,这种差距更加明显。这是由于当注入率不断增加时,3D Mesh网络中的靠外层的节点数量不足,使得信息无法传递到里层节点,导致了网络阻塞,从而需要大量的时间去处理;当注入率增长到0.012 时,五维超立方裂变拓扑结构平均延时出现了上升的趋势,此时五维超立方裂变拓扑结构的平均延时比3D Mesh拓扑结构低85.1%。
4.3.2 局部负载模式下平均延时对比分析
由仿真实验数据得到了五维超立方裂变拓扑结构与3D Mesh拓扑结构在局部负载模式下,平均延时与注入率之间的关系曲线,如图7所示。
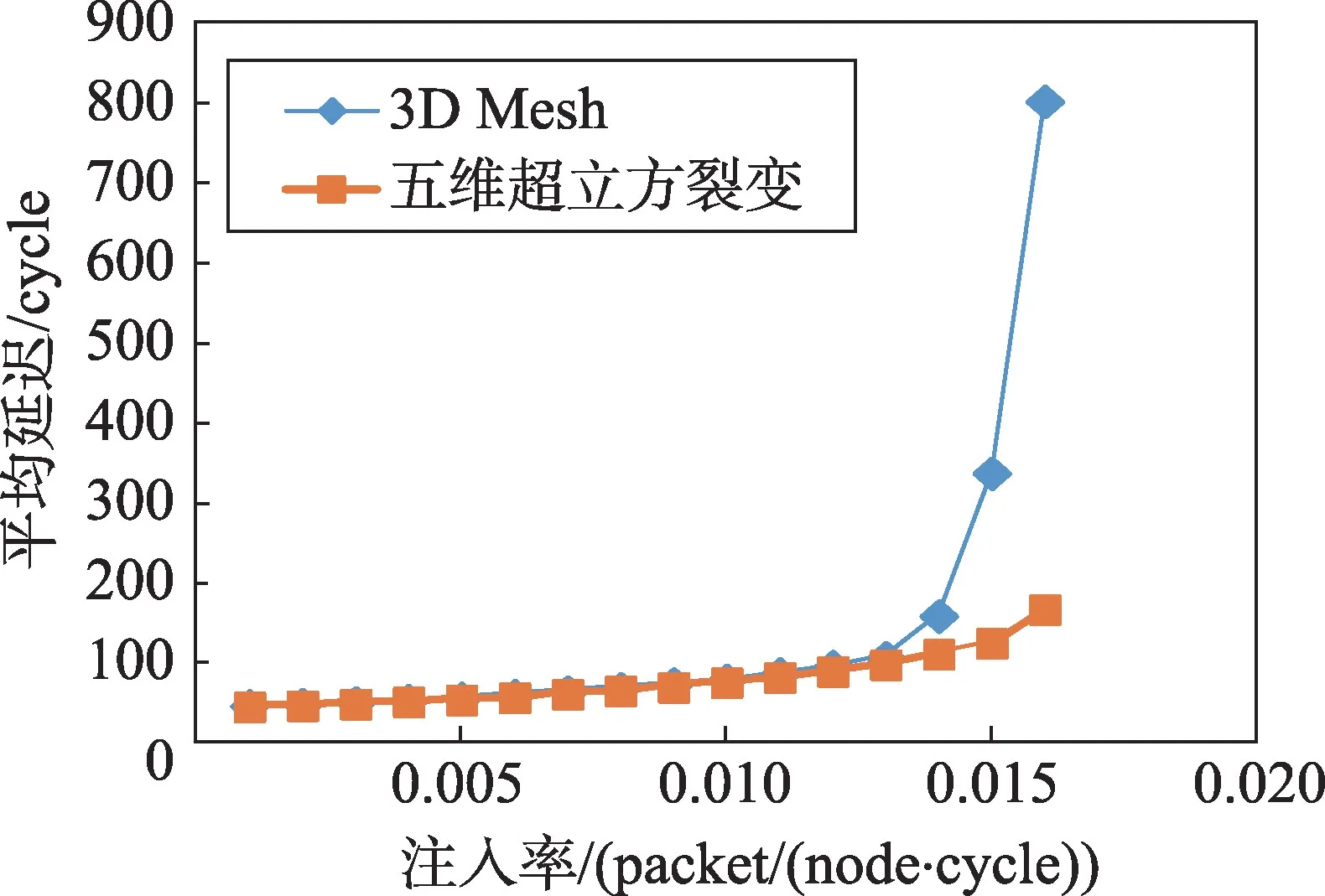
Fig.7 Contrast of average latency under localized pattern图7 局部负载下平均延时的对比
由图7可知,在局部负载下,当注入率小于0.013时,五维超立方裂变拓扑结构和3D Mesh拓扑结构的平均延时都较小,且基本一致;当注入率达到0.014~0.016 区间时,3D Mesh 拓扑结构的平均延时呈现阶梯式增长,从注入率达到0.014开始,3D Mesh拓扑结构就逐渐达到了饱和状态;当注入率达到0.016 时,五维超立方裂变拓扑结构的平均延时比3D Mesh 拓扑结构的平均延时低79.1%。
4.4 平均跳数对比分析
4.4.1 均匀负载模式下平均跳数对比分析
由仿真实验得到了均匀负载下,五维超立方裂变拓扑结构网络和3D Mesh 拓扑结构网络的接收数据包总数和平均跳数的数据,如表3所示。
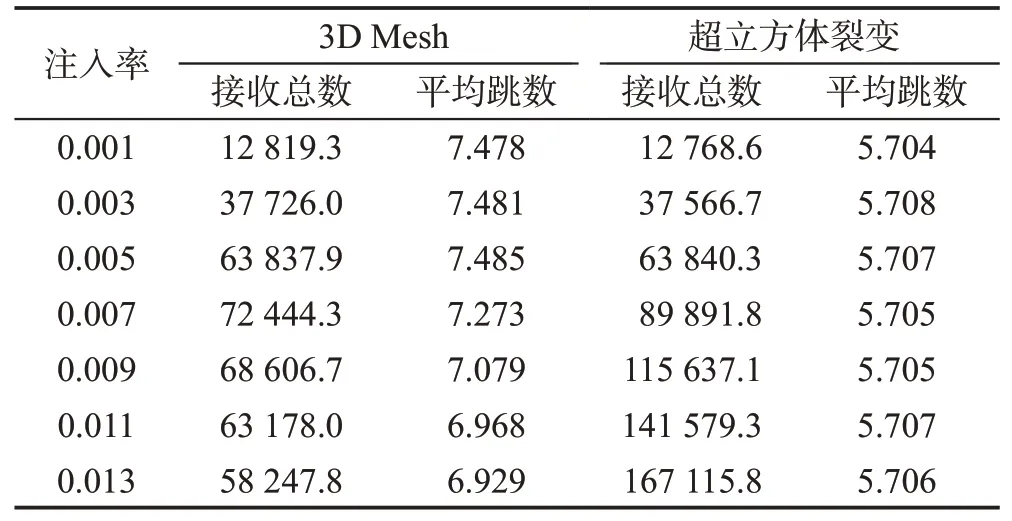
Table 3 Contrast under uniform pattern表3 均匀负载模式下的对比
由表3可知,在均匀负载下,当注入率小于0.007时,五维超立方裂变拓扑结构和3D Mesh拓扑结构接收包总数都呈线性增长;当注入率达到0.007 附近时,3D Mesh 拓扑结构达到饱和,五维超立方裂变拓扑结构在仿真实验数据范围内没有达到饱和;当注入率超过0.007时,由于网络堵塞,3D Mesh出现大量丢包现象,五维超立方裂变拓扑结构的平均跳数比3D Mesh拓扑结构少21.5%。
4.4.2 局部负载模式下平均跳数对比分析
由仿真实验得到了局部负载下,五维超立方裂变拓扑结构网络和3D Mesh 拓扑结构网络的接收数据包总数和平均跳数的数据,如表4所示。
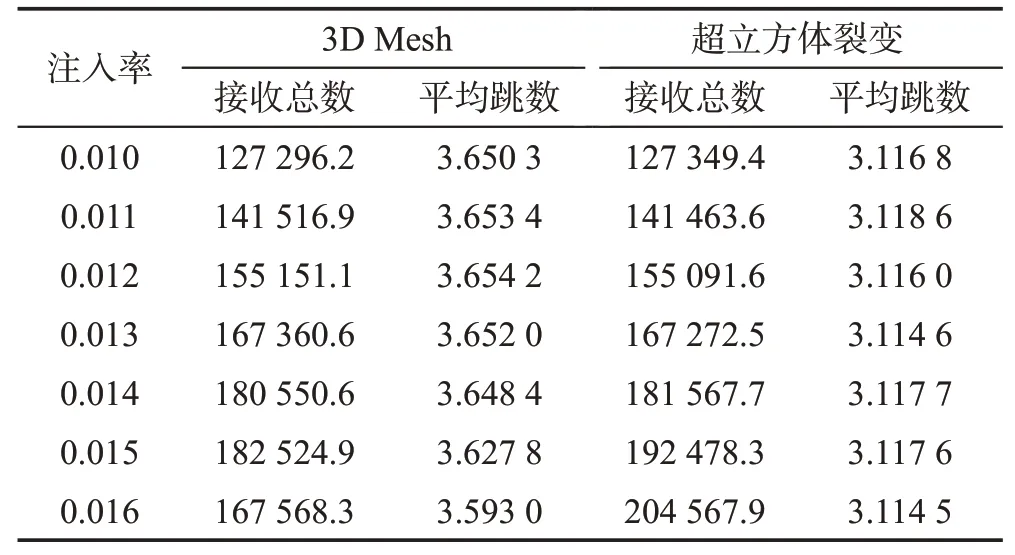
Table 4 Contrast under localized pattern表4 局部负载模式下的对比
根据仿真实验数据可知,在局部负载下,注入率小于0.015时,两种网络拓扑结构接收包数呈线性增长;而当注入率达到0.016 时,3D 拓扑结构开始出现大量丢包现象,而五维超立方裂变拓扑结构则仍然保持线性增长,五维超立方裂变拓扑结构的平均跳数比3D Mesh少13.3%。
5 结束语
基于高维超立方拓扑结构的片上网络布局和连线都很复杂,节点度数随着维数的增加而增加,网络通讯性能随之下降。为了解决这一瓶颈问题,本文对超立方片上网络拓扑结构进行了改造,提出一种三维片上网络新型拓扑结构——三维片上网络五维超立方裂变拓扑结构。与相同规模的超立方网络拓扑结构进行了比较,五维超立方裂变拓扑结构在保留超立方网络拓扑结构优点的同时,连线更少、更规则。但是高维超立方裂变拓扑结构相对于3D Mesh 拓扑结构来说物理链路较为复杂,在实际生产芯片时,需要对芯片网络布线技术有一定的要求。仿真实验结果表明,本文提出的三维片上网络五维超立方裂变拓扑结构与经典3D Mesh网络拓扑结构相比,具有更大的吞吐量、更大的网络流量及更低的平均延时。
